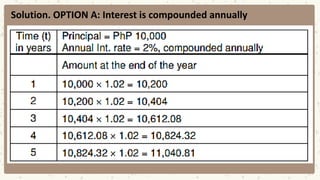
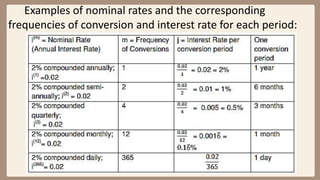
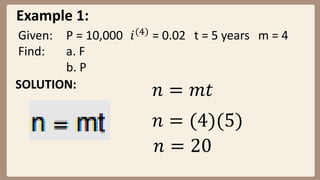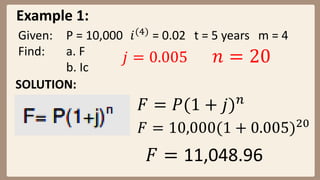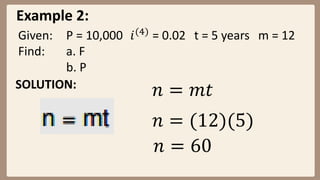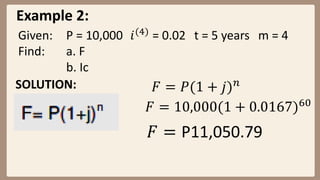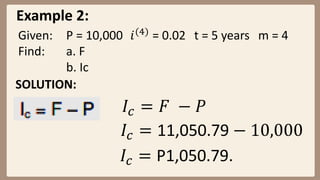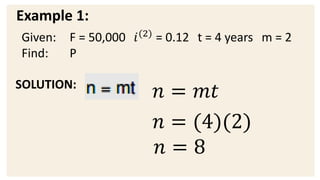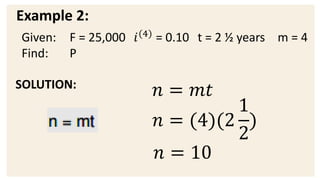This document provides examples and explanations for computing compound interest when it is compounded more than once per year. It defines key terms like nominal interest rate, frequency of conversion, and interest rate per conversion period. Examples are provided to demonstrate calculating maturity value, interest, and present value for principal amounts compounded quarterly, semi-annually, and monthly over various time periods. Practice problems at the end involve using the concepts and formulas taught to solve for unknown values in compound interest scenarios.

2. At the end of the lesson,
the learner is able to
compute maturity value,
interest, and present
value, and solve
problems involving
compound interest
when compound
interest is computed
more than once a year.

3. Lesson Outline:
1.Compounding more than once a year
2.Maturity value, interest, and present value
when compound interest is computed
more than once a year

4. Sometimes, interest may be compounded more than once a year.
Consider the following example.
Example 1. Given a principal of PhP 10,000, which of the
following options will yield greater interest after 5 years:
OPTION A: Earn an annual interest rate of 2% at the end
of the year, or
OPTION B: Earn an annual interest rate of 2% in two
portions—1% after 6 months, and 1% after another 6
months?

5. Solution. OPTION A: Interest is compounded annually

6. OPTION B: Interest is compounded semi-annually, or every 6 months. Under
this option, the interest rate every six months is 1% (2% divided by 2).

7. Option B will give the
higher interest after 5 years.
If all else is equal, a more
frequent compounding will
result in a higher interest,
which is why Option B gives
a higher interest than
Option A.

8. Definition of Terms:
• Frequency of conversion (m) – number of conversion
periods in one year
• Conversion or interest period – time between successive
conversions of interest
• Total number of conversion periods n
n = mt = (frequency of conversion) x (time in years)
• Nominal rate (𝒊(𝒎)
) – annual rate of interest
• Rate (j) of interest for each conversion period

9. Examples of nominal rates and the corresponding
frequencies of conversion and interest rate for each period:

10. FORMULA:
OR:

11. Example 1:
Find the maturity value and interest
if P10,000 is deposited in a bank at 2%
compounded quarterly for 5 years.
Given: P = 10,000 𝑖(4)
= 0.02
t = 5 years m = 4
Find: a. F b. Ic

12. Example 1:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. Ic
SOLUTION: 𝑗 =
𝑖(4)
𝑚
𝑗 =
0.02
4
𝑗 = 0.005

13. Example 1:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. P
SOLUTION:
𝑛 = 𝑚𝑡
𝑛 = (4)(5)
𝑛 = 20

14. Example 1:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. Ic
SOLUTION:
𝐹 = 𝑃(1 + 𝑗)𝑛
𝐹 = 10,000(1 + 0.005)20
𝐹 = 11,048.96
𝑗 = 0.005 𝑛 = 20

15. Example 1:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. Ic
SOLUTION: 𝐼𝑐 = 𝐹 − 𝑃
𝐼𝑐 = 11,048.96 − 10,000
𝐼𝑐 = 1,048.96

16. Example 2:
Find the maturity value and interest
if P10,000 is deposited in a bank at 2%
compounded monthly for 5 years.
Given: P = 10,000 𝑖(12)
= 0.02 t = 5 years m = 12
Find: a. F
b. Ic

17. Example 2:
Given: P = 10,000 𝑖(12)
= 0.02 t = 5 years m = 12
Find: a. F
b. Ic
SOLUTION:
𝑗 =
𝑖(12)
𝑚
𝑗 =
0.02
12
𝑗 = 0.0166 …

18. Example 2:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 12
Find: a. F
b. P
SOLUTION:
𝑛 = 𝑚𝑡
𝑛 = (12)(5)
𝑛 = 60

19. Example 2:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. Ic
SOLUTION: 𝐹 = 𝑃(1 + 𝑗)𝑛
𝐹 = 10,000(1 + 0.0167)60
𝐹 = P11,050.79

20. Example 2:
Given: P = 10,000 𝑖(4)
= 0.02 t = 5 years m = 4
Find: a. F
b. Ic
SOLUTION:
𝐼𝑐 = 𝐹 − 𝑃
𝐼𝑐 = 11,050.79 − 10,000
𝐼𝑐 = P1,050.79.

21. Example 3:
Cris borrows P50,000 and promises to
pay the principal and interest at 12%
compounded monthly. How much must
he repay after 6 years?
Given: P = P50,000 𝑖(12)
= 0.12 t = 6 years m = 12
Find: F

22. Example 3:
SOLUTION:
Given: P = P50,000 𝑖(12)
= 0.12 t = 6 years m = 12
Find: F
𝑭 = 𝑷(𝟏 +
𝒊(𝟏𝟐)
𝒎
)𝒎𝒕
𝐹 = 50,000(1 +
0.12
12
) 12 (6)
𝐹 = 50,000(1.01)72 𝑭 = 𝑷𝟏𝟎𝟐, 𝟑𝟓𝟒. 𝟗𝟕
Thus, Cris must
pay P102,354.97
after 6 years.

23. PRESENT VALUE

24. Example 1:
Find the present value of P50,000
due in 4 years if money is invested at
12% compounded semi-annually.
Given: F = 50,000 𝑖(2)
= 0.12 t = 4 years m = 2
Find: P

25. Example 1:
SOLUTION:
𝑗 =
𝑖(2)
𝑚
𝑗 =
0.12
2
𝑗 = 0.06
Given: F = 50,000 𝑖(2)
= 0.12 t = 4 years m = 2
Find: P

26. Example 1:
SOLUTION:
𝑛 = 𝑚𝑡
𝑛 = (4)(2)
𝑛 = 8
Given: F = 50,000 𝑖(2)
= 0.12 t = 4 years m = 2
Find: P

27. Example 1:
SOLUTION:
𝑷 =
𝑭
(𝟏 + 𝒋)𝒏
Given: F = 50,000 𝑖(2)
= 0.12 t = 4 years m = 2
Find: P
𝑃 =
50,000
(1 + 0.06)8
𝑃 =
50,000
(1.06)8 𝑷 = 𝑷𝟑𝟏, 𝟑𝟕𝟎. 𝟔𝟐

28. Example 2:
What is the present value of P25,000
due in 2 years and 6 months if money
is worth 10% compounded quarterly?
Given: F = 25,000 𝑖(4)
= 0.10 t = 2 ½ years m = 4
Find: P

29. Example 2:
SOLUTION:
𝑗 =
𝑖(4)
𝑚
𝑗 =
0.10
4
𝑗 = 0.025
Given: F = 25,000 𝑖(4)
= 0.10 t = 2 ½ years m = 4
Find: P

30. Example 2:
SOLUTION:
𝑛 = 𝑚𝑡
𝑛 = (4)(2
1
2
)
𝑛 = 10
Given: F = 25,000 𝑖(4)
= 0.10 t = 2 ½ years m = 4
Find: P

31. Example 2:
SOLUTION:
𝑷 =
𝑭
(𝟏 + 𝒋)𝒏
𝑃 =
25,000
(1 + 0.025)10
𝑃 =
25,000
(1.025)10 𝑷 = P19,529.96
Given: F = 25,000 𝑖(4)
= 0.10 t = 2 ½ years m = 4
Find: P

32. SEATWORK: (1 whole)
Solve the following problems on compound interest.
1. Cian lends P45,000 for 3 years at 5%
compounded semi-annually. Find the future
value and interest of this amount.
2.Tenten deposited P10,000 in bank which gives
1% compounded quarterly and let it stay there
for 5 years. Find the maturity value and
interest.

33. SEATWORK: (1 whole)
Solve the following problems on compound interest.
3. How much should you set aside and invest in a
fund earning 9% compounded quarterly if you
want to accumulate P200,000 in 3 years and 3
months?
4. How much should you deposit in a bank paying 2%
compounded quarterly to accumulate an amount
of P80,000 in 5 years and 9 months?

34. 5. Miko has P250,000 to invest at 6% compounded
monthly. Find the maturity value if he invests for
(a) 2 years? (b) 12 years? (c) How much is the
additional interest earned due to the longer
time.
6. Yohan sold his car and invested P300,000 at 8.5%
compounded quarterly. Find the maturity value
if he invests for (a) 3 years? (b) 6 years? (c) How
much is the additional interest earned due to the
longer time.

35. 7. Maryam is planning to invest P150,000. Bank A is
offering 7.5% compounded semi-annually while
Bank B is offering 7% compounded monthly. If she
plans to invest this amount for 5 years, in which
bank should she invest?
8. Yani has a choice to make short term investments
for her excess cash P60,000. She can invest at 6%
compounded quarterly for 6 months or (b) 5%
compounded semi-annually fo 1 year. Which is
larger?