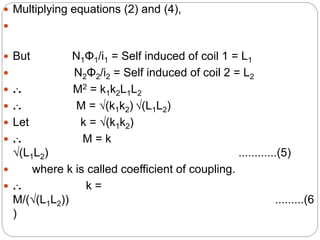
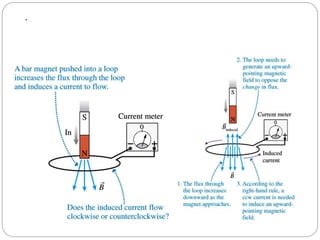
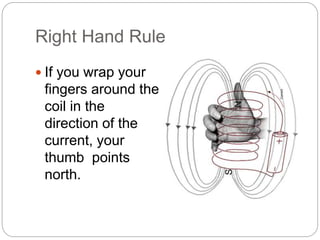
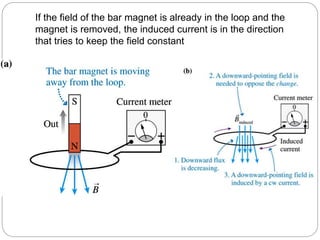
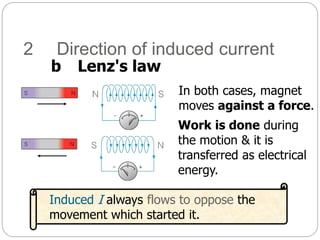
Lenz's law describes the direction of induced current in a coil due to a changing magnetic flux. The coefficient of coupling (k) indicates the amount of flux from one coil that is linked to another coupled coil. k is defined as the ratio of the actual mutual inductance between the coils to the maximum possible mutual inductance. When k=1, the coils are perfectly coupled and the mutual inductance is at its maximum value. When coils are loosely coupled, k is very small and only a small fraction of flux links between the coils. Lenz's law states that any change in magnetic flux through a coil will induce a current whose direction opposes the change in flux.

1. SUBJECT-LENZ’S LAW AND COEFFICIENT
OF COUPLING
GUIDED BY:-
ANKUR SIR
ELEMENTS OF
ELECTRICAL
ENGINEERING

2. When two coils are magnetically coupled
then coefficient of coupling indicates that
the how much flux linked from coil-1 to
coil-2..
Practically not all flux linked from coil1-
coil2 but some flux linked with coil itself.
so,it is indicated by its fraction K
COEFFICIENT OF COUPLING

3. When supply is given to coil-1 then
current I1 will flow and when it chaged
by variable resistance which result
flux θ produce in coil-1,now it linked
with coil-2,resulting flux θ2 will
produce in coil-2 is indicated
by θ2=k θ2 and similarly,when supply
given to coil-2 then how much flux
linked from coil-2 to coil-1 is indicated
by θ1=k θ2

4.  Due to current i1, the flux produced is Φ1 which links with both
the coils. Then from the previous knowledge mutual inductance
between two coils can be written as
 M =
N1 Φ21/i1 ...............(1)
 where Φ21 is the part of the flux Φ1 linking with coil 2.
Hence we can write, Φ21 = k1 Φ1.
 ... M = N1 (
k1 Φ1)/i1 .................(2)
 Similarly due to current i2, the flux produced is Φ2 which
links with both the coils. Then the mutual inductance between
two coils can be written as
 M =
N2 Φ21/i2 .........(3)
 where Φ21 is the part of the flux Φ2 linking with coil 1.
Hence we can write Φ21 = k2 Φ2.
 ... M =

5.  Multiplying equations (2) and (4),

 But N1Φ1/i1 = Self induced of coil 1 = L1
 N2Φ2/i2 = Self induced of coil 2 = L2
 ... M2 = k1k2L1L2
 ... M = √(k1k2) √(L1L2)
 Let k = √(k1k2)
 ... M = k
√(L1L2) ............(5)
 where k is called coefficient of coupling.
 ... k =
M/(√(L1L2)) .........(6
)

6.  The coefficient of coupling gives idea about the magnetic
coupling between the two coils. So when the entire flux in
one coil links with the other, the coupling coefficient is
maximum. The maximum value of k is unity. Thus when k =
1, the coupled coils are called tightly or perfectly coupled
coils. Also the mutual inductance between the two coils is
maximum with k =1. The maximum value of the mutual
inductance is given by
 M
= √(L1L2) ..............(7
)
 When the two coils are at greater distance in space,
the value of k is very small. Then the two coils are called
loosely coupled coils.

7.  From equations (6) and (7), the coefficient of coupling can
be alternatively defined as the ratio of the actual mutual
inductance present between the two coils to the maximum
possible value of the mutual inductance.
 The coefficient of coupling between the two coils can
also be expressed interms of the reactance offered by the
self inductance and mutual inductance as

8. Heinrich F.E. Lenz
 Russian physicist
 (1804-1865)
 1834 Lenz’s Law
 There is an induced
current in a closed
conducting loop if and
only if the magnetic flux
through the loop is
changing. The direction
of the induced current is
such that the induced
magnetic field always
opposes the change in
the flux.

9. .

10. Right Hand Rule
 If you wrap your
fingers around the
coil in the
direction of the
current, your
thumb points
north.

11. If the field of the bar magnet is already in the loop and the
magnet is removed, the induced current is in the direction
that tries to keep the field constant

12. 2 Direction of induced current
In both cases, magnet
moves against a force.
Work is done during
the motion & it is
transferred as electrical
energy.
Induced I always flows to oppose the
movement which started it.
b Lenz's law

13. THANK YOU
PREPARED BY;-
MOHIT G TALREJA
151080106028