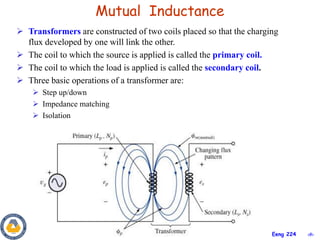
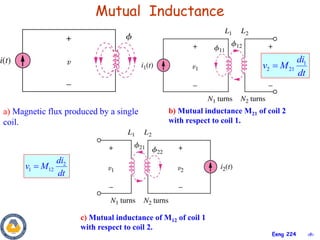
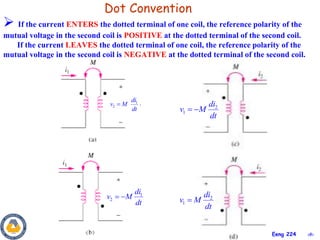
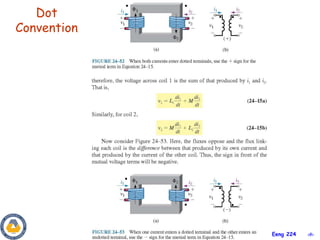
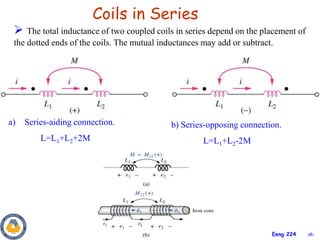
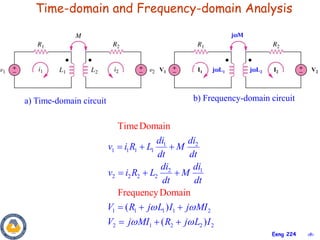
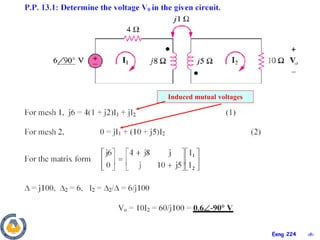
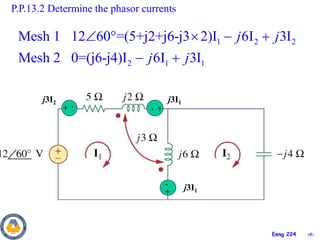
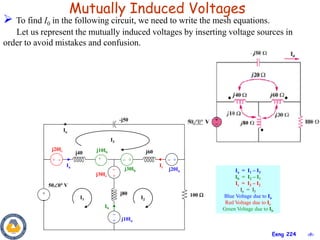
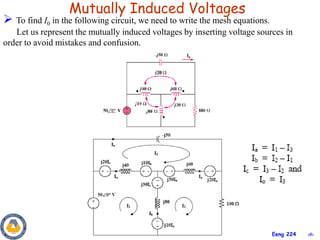
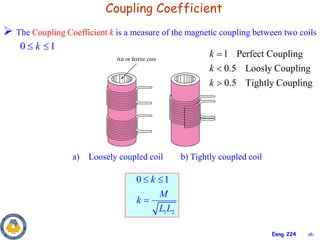
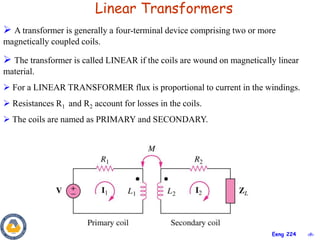
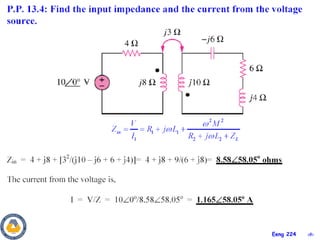
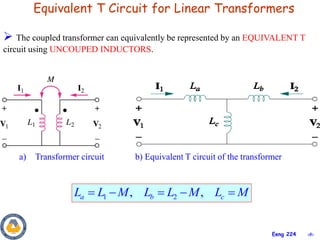
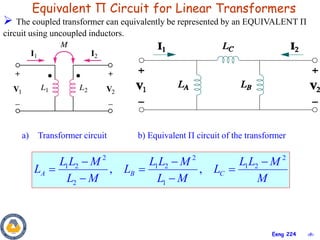
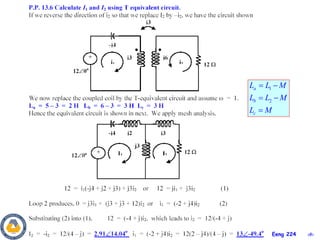
This document covers material about magnetically coupled circuits and transformers. It discusses key topics like mutual inductance, transformer operations of step up/down and impedance matching, deriving and analyzing circuits using mutual inductance representations, determining energy in coupled circuits, and modeling transformers using equivalent T-circuits and Π-circuits. The objectives are to understand magnetically coupled circuits, mutual inductance, analyzing circuits involving linear and ideal transformers, and applying the concepts to transformers as isolation devices and power distribution.

1. ‹#›
Eeng 224
Magnetically Coupled Circuits
Chapter Objectives:
 Understand magnetically coupled circuits.
 Learn the concept of mutual inductance.
 Be able to determine energy in a coupled circuit.
 Learn how to analyze circuits involving linear and ideal transformers.
 Be familiar with ideal autotransformers.
 Learn how to analyze circuits involving three-phase transformers.
 Apply what is learnt to transformer as an isolation device and power
distribution

2. ‹#›
Eeng 224
Mutual Inductance
 Transformers are constructed of two coils placed so that the charging
flux developed by one will link the other.
 The coil to which the source is applied is called the primary coil.
 The coil to which the load is applied is called the secondary coil.
 Three basic operations of a transformer are:
 Step up/down
 Impedance matching
 Isolation

3. ‹#›
Eeng 224
Mutual Inductance Devices

4. ‹#›
Eeng 224
Mutual Inductance
1 11 21
1 1 1
( )
d d
v N N
dt dt
  

  2 12 22
2 2 2
( )
d d
v N N
dt dt
  

 
 When two coils are placed close to each other, a changing flux in one coil will cause
an induced voltage in the second coil. The coils are said to have mutual inductance M,
which can either add or subtract from the total inductance depending on if the fields are
aiding or opposing.
 Mutual inductance is the ability of one inductor to induce a voltage across a
neighboring inductor.

5. ‹#›
Eeng 224
b) Mutual inductance M21 of coil 2
with respect to coil 1.
Mutual Inductance
a) Magnetic flux produced by a single
coil.
c) Mutual inductance of M12 of coil 1
with respect to coil 2.
2
1 12
di
v M
dt

1
2 21
di
v M
dt


6. ‹#›
Eeng 224
Mutual Inductance
 Mutual inductances M12 and M21 are equal.
 They are referred as M.
 We refer to M as the mutual inductance between two coils.
 M is measured in Henry’s.
 Mutual inductance exists when two coils are close to each other.
 Mutual inductance effect exist when circuits are driven by time varying sources.
 Recall that inductors act like short circuits to DC.
12 21
M M M
 

7. ‹#›
Eeng 224
Dot Convention
 If the current ENTERS the dotted terminal of one coil, the reference polarity of the
mutual voltage in the second coil is POSITIVE at the dotted terminal of the second coil.
If the current LEAVES the dotted terminal of one coil, the reference polarity of the
mutual voltage in the second coil is NEGATIVE at the dotted terminal of the second coil.
1
2
di
v M
dt

1
2
di
v M
dt
 
2
1
di
v M
dt
 
2
1
di
v M
dt


8. ‹#›
Eeng 224
Dot
Convention

9. ‹#›
Eeng 224
Coils in Series
a) Series-aiding connection.
L=L1+L2+2M
b) Series-opposing connection.
L=L1+L2-2M
 The total inductance of two coupled coils in series depend on the placement of
the dotted ends of the coils. The mutual inductances may add or subtract.

10. ‹#›
Eeng 224
Time-domain and Frequency-domain Analysis
1 2
1 1 1 1
2 1
2 2 2 2
1 1 1 1 2
2 1 2 2 2
TimeDomain
FrequencyDomain
( )
( )
di di
v i R L M
dt dt
di di
v i R L M
dt dt
V R j L I j MI
V j MI R j L I
 
 
  
  
  
  
V1 V2
I1 I2
jL1 jL2
jM
a) Time-domain circuit b) Frequency-domain circuit

11. ‹#›
Eeng 224
Induced mutual voltages

12. ‹#›
Eeng 224
Induced mutual voltages

13. ‹#›
Eeng 224
+
-
+
-
+
-
j3I1
j3I1
j3I2
P.P.13.2 Determine the phasor currents
1 2 2
2 1 1
Mesh 1 12 60 =(5+j2+j6-j3 2)I 6I 3I
Mesh 2 0=(j6-j4)I 6I 3I
j j
j j
    
 

14. ‹#›
Eeng 224
Mutually Induced Voltages
 To find I0 in the following circuit, we need to write the mesh equations.
Let us represent the mutually induced voltages by inserting voltage sources in
order to avoid mistakes and confusion.
+


+
 +
I1 I2
Io
j20Ic
100 
500 V
I3

+
 +
+

+ 
j10Ib
j40
j30Ic
j80
j10Ia
j20Ia
j60
j30Ib
-j50
Ia
Ib
Ic
Ia = I1 – I3
Ib = I2 – I1
Ic = I3 – I2
Io = I3
Blue Voltage due to Ia
Red Voltage due to Ic
Green Voltage due to Ib

15. ‹#›
Eeng 224
Mutually Induced Voltages
 To find I0 in the following circuit, we need to write the mesh equations.
Let us represent the mutually induced voltages by inserting voltage sources in
order to avoid mistakes and confusion.

16. ‹#›
Eeng 224
Energy in a Coupled Circuit
2 2
1 1 2 2 1 2
1 1
2 2
w Li L i Mi i

 
 The total energy w stored in a mutually coupled inductor is:
 Positive sign is selected if both currents ENTER or LEAVE the dotted terminals.
 Otherwise we use Negative sign.

17. ‹#›
Eeng 224
Coupling Coefficient
a) Loosely coupled coil b) Tightly coupled coil
1 2
0 1
k
M
k
L L
 

 The Coupling Coefficient k is a measure of the magnetic coupling between two coils
0 1
k
 
1 Perfect Coupling
0.5 Loosly Coupling
0.5 Tightly Coupling
k
k
k




18. ‹#›
Eeng 224
Linear Transformers
 A transformer is generally a four-terminal device comprising two or more
magnetically coupled coils.
 The transformer is called LINEAR if the coils are wound on magnetically linear
material.
 For a LINEAR TRANSFORMER flux is proportional to current in the windings.
 Resistances R1 and R2 account for losses in the coils.
 The coils are named as PRIMARY and SECONDARY.

19. ‹#›
Eeng 224
Reflected Impedance for Linear Transformers
1 1 1 2
1 2 2 2
( )
0 ( )
L
V R j L I j MI
j MI R j L Z I
 
 
  
    
2 2
1 1 1 1
1 2 2
in R
L
V M
Z R j L R j L Z
I R j L Z

 

      
 
2 2
2 2
REFLECTED IMPEDANCE
R
L
M
Z
R j L Z



 
• Secondary impedance seen from the primary side is the Reflected Impedance.
 Let us obtain the input impedance as seen from the source,
ZR

20. ‹#›
Eeng 224

21. ‹#›
Eeng 224
Equivalent T Circuit for Linear Transformers
 The coupled transformer can equivalently be represented by an EQUIVALENT T
circuit using UNCOUPED INDUCTORS.
1 2
, ,
a b c
L L M L L M L M
    
a) Transformer circuit b) Equivalent T circuit of the transformer

22. ‹#›
Eeng 224
Equivalent П Circuit for Linear Transformers
 The coupled transformer can equivalently be represented by an EQUIVALENT П
circuit using uncoupled inductors.
2 2 2
1 2 1 2 1 2
2 1
, ,
A B C
L L M L L M L L M
L L L
L M L M M
  
  
 
a) Transformer circuit b) Equivalent Π circuit of the transformer

23. ‹#›
Eeng 224
1
2
a
b
c
L L M
L L M
L M
 
 
