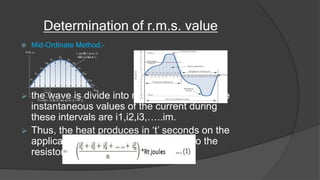
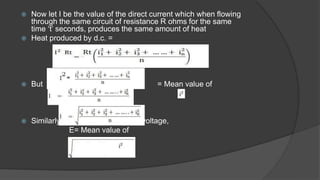
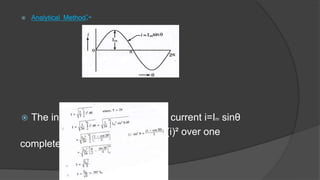
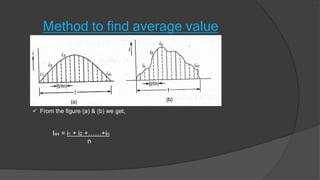
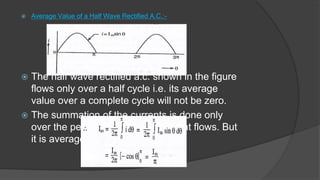
This document discusses root mean square (RMS) value, average value, form factor, and peak factor of alternating quantities. It defines each term and describes several methods to calculate RMS value and average value, including the mid-ordinate method and analytical method. For a sinusoidal waveform, the RMS value is 0.707 times the peak value, the average value is 0.637 times the peak value, the form factor is the ratio of RMS to average value (which is 1.11 for sinusoidal), and the peak factor is the ratio of peak value to RMS value (which is 1.414 for sinusoidal).

1. 1

2. Topic :r.m.s. value , average value , form factor , peak factor
Created by :-
akshat raval
151080106022
civil
2nd sem.

3. contents
 R.M.S VALUE :- DETERMINATION OF
R.M.S. VALUE
1. Mid-Ordinate Method
2.Analytical Method
3.R.M.S. Value of A Half Wave Rectified A.C.
 AVERAGE VALUE OF AN ALTERNATING
QUANTITY :-
1.Mid-ordinate method
2.Analytical Method
3.Half wave rectified A.C.
 Form Factor
 Peak Factor

4. Root mean square value
 The R.M.S. value of the a.c. current is also called the effective value.
 The R.M.S. value of an a.c. is the equivalent steady current which
when allowed to flow through a given period of time prouducess the
same amount of heat as produced by the alternating current. When it
flows through the same circuit for the same period of time.

5.  We consider a simple example as in the figure which illustrates the
significance of the R.M.S. value of an alternating current.
 L is a metal filament lamp. S is a switch. Initially the switch S is closed
on contact X, so that the lamp is connected to the a.c. supply. The
brightness of the filament lamp is noted.
 Next, the switch S is closed on contact Y and the resistor value is
varied so that the lamp gives the same brightness as with a.c. When
the lamp gives the same brightness, the reading on the moving coil
ammeter A is noted. This reading gives nothing but the direct current
that produces the same heating effect as produced by the alternating
current.
 If the ammeter reads 0.5 A when the equality of brightness is attained,
the R.M.S. value of the alternating current 0.5 A.

6. Determination of r.m.s. value
 Mid-Ordinate Method:-
 the wave is divide into m equal intervals. The
instantaneous values of the current during
these intervals are i1,i2,i3,…..im.
 Thus, the heat produces in ‘t’ seconds on the
application of the alternating current to the
resistor R.

7.  Now let I be the value of the direct current which when flowing
through the same circuit of resistance R ohms for the same
time ‘t’ seconds, produces the same amount of heat
 Heat produced by d.c. =
 But = Mean value of
 Similarly R.M.S. value of an a.c. voltage,
E= Mean value of
Mean value of

8.  Analytical Method:-
 The instantaneous value of the current i=Im sinθ
Thus the mean value of (i)² over one
complete cycle will be

9.  Thus the R.M.S. value of the A.C. sinusoidal current.
I=0.707*Im (max. value of the current)
 R.M.S Value of a Half Wave Rectified A.C.:-
A half wave rectified alternating current is
one in which the current flows only during one half of a cycle and
remains suppressed during the other half of that cycle. Figure
shows a half wave rectified waveform.
the dotted path shows the suppressed half cycle
So here the summation of the instantaneous values of the
current is carried out only for the period for which the current
flows i.e. from 0 to π but it would be averaged over the entire
cycle.

11. Average Value Of An Alternating Quantity
 Average value of an alternating quantity is given by that
steady current which when flowing through a given circuit for
a given time, transfers across that circuit the same amount of
charge as is transferred by the alternating current when it
flows through the same circuit for the same time.
 The average value of an alternating voltage or current is
given by the arithmetic mean of the ordinates of that quantity
at equal intervals over a half cycle.
 This is because the arithmetic mean found over one complete
cycle of a symmetrical sinusoidal or non-sinusoidal waveform
is zero. So, the average value of a symmetrical alternating
quantity is found only over a half cycle.

12. Method to find average value
 From the figure (a) & (b) we get,
Iav = i1 + i2 +……+in
n

13.  Analytical Method:-
Equation of the alternating current I = Im sinθ.
Thus the average value of a symmetrical a.c. is 0.637 Im.

14.  Average Value of a Half Wave Rectified A.C.:-
 The half wave rectified a.c. shown in the figure
flows only over a half cycle i.e. its average
value over a complete cycle will not be zero.
 The summation of the currents is done only
over the period for which the current flows. But
it is averaged over the entire cycle.

15. Form factor
 Form factor is defined as the ratio of the R.M.S. value
to the average value of an alternating quantity. It is
denoted by Kf.
Kf = R.M.S. value
average value
 Thus for a symmetrical sinusoidal wave,
Kf = .707 Im = 1.11
.637 Im
 Having knowledge of the form factor, the R.M.S. value
can be found from the average value and vice-versa.

16. Peak factor (Ka)
 Peak factor is defined as the ratio of the peak value to the R.M.S.
value of an alternating quantity.
 Thus for a symmetrical sinusoidal wave,
Ka = Im = Im = 1.414
Irms .707 Im
 Peak factor is also called the crest factor or the amplitude factor.
 Normally the rms value of an alternating quantity is specified. If the
peak factor is known, the maximum value can be found.
 The knowledge of the peak factor is of importance :
1. For measuring the iron losses as these losses depend upon the
peak value of the flux.
2. In dielectric insulation testing, because the dielectric stresses
during insulation testing are proportional to the peak value of the
applied voltage.

17. 17