Download to read offline
Uploaded byAIMST University
Lecture Notes: EEEC4340318 Instrumentation and Control Systems - Fundamentals of Feedback
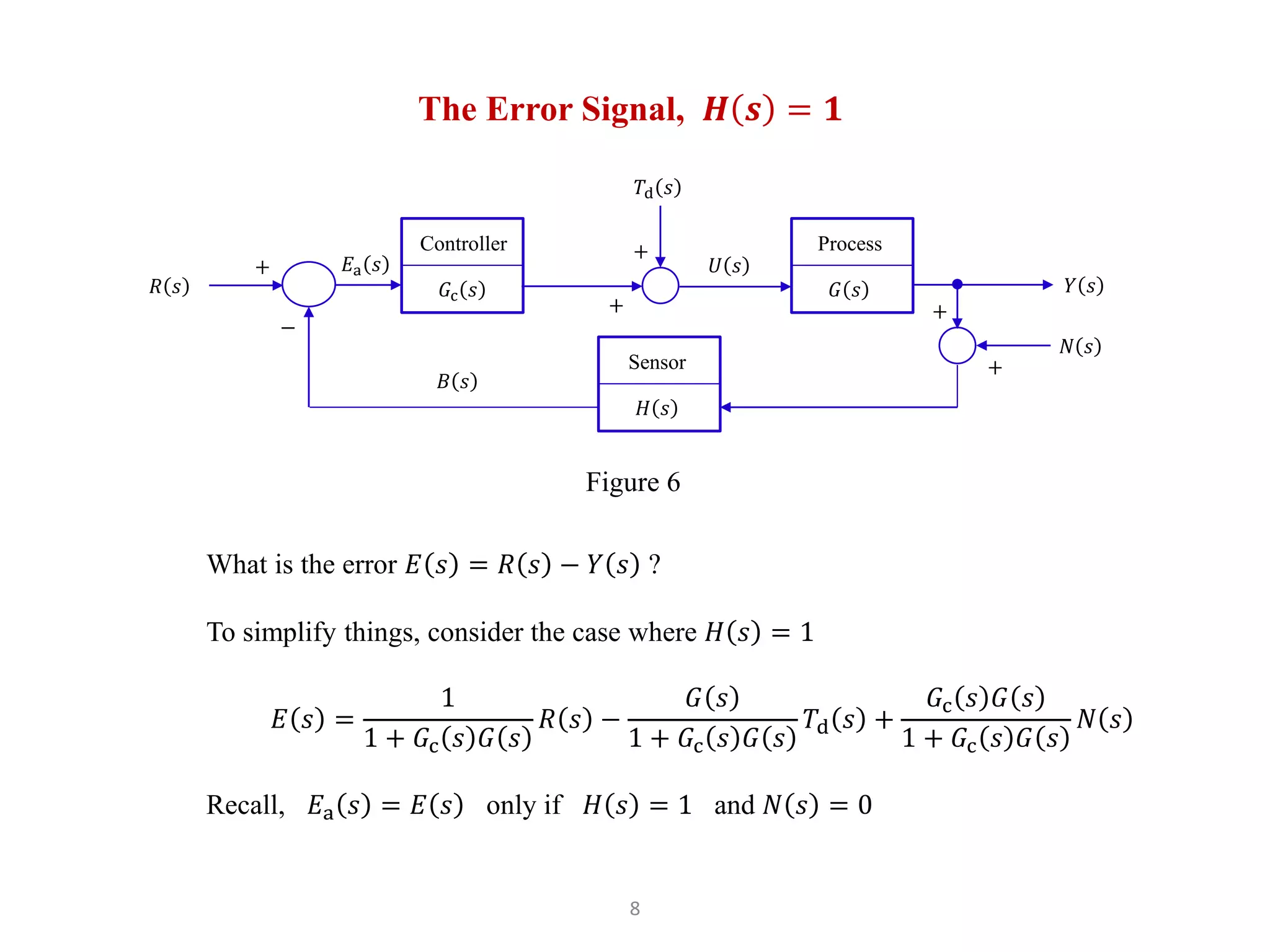
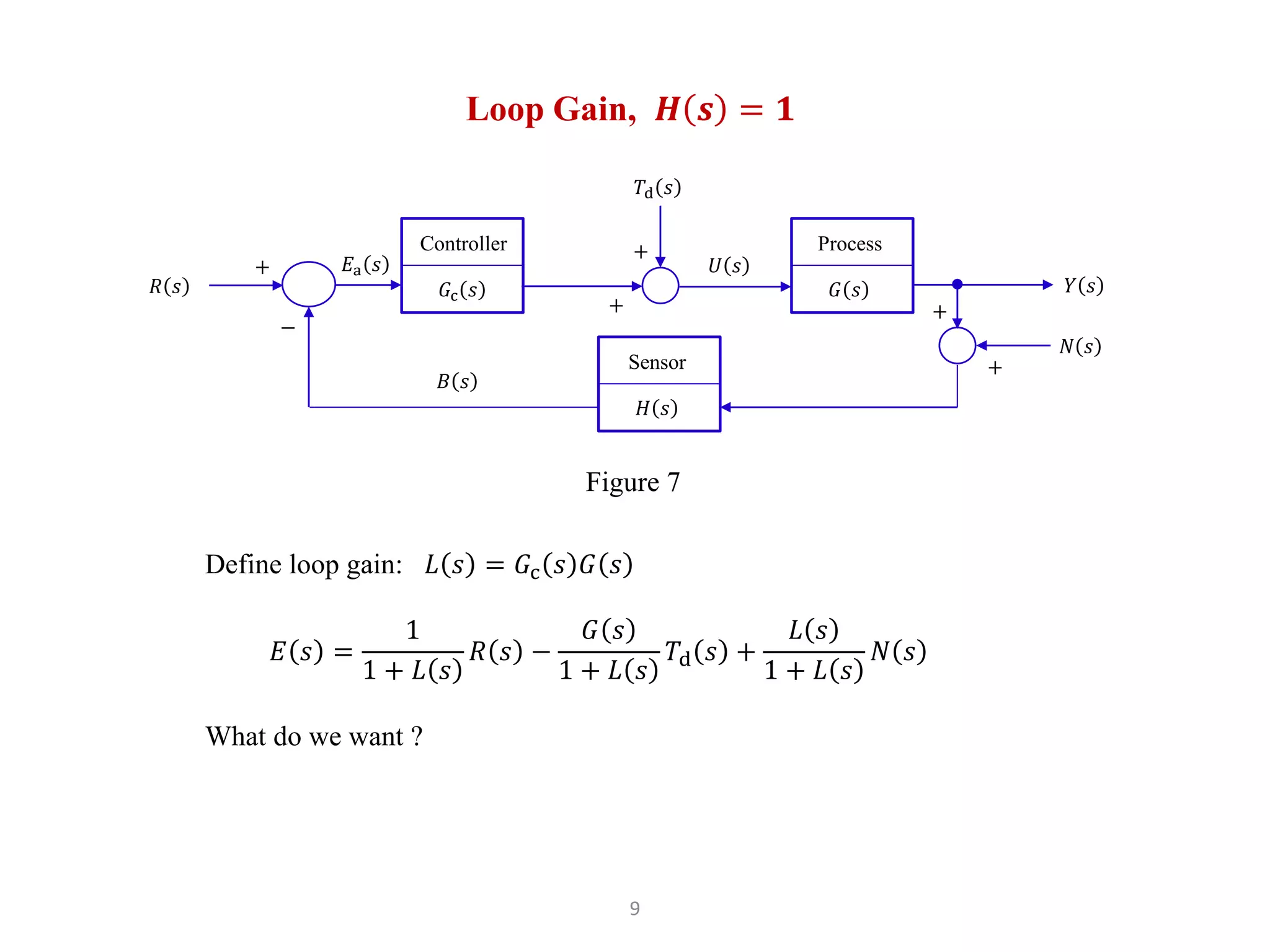
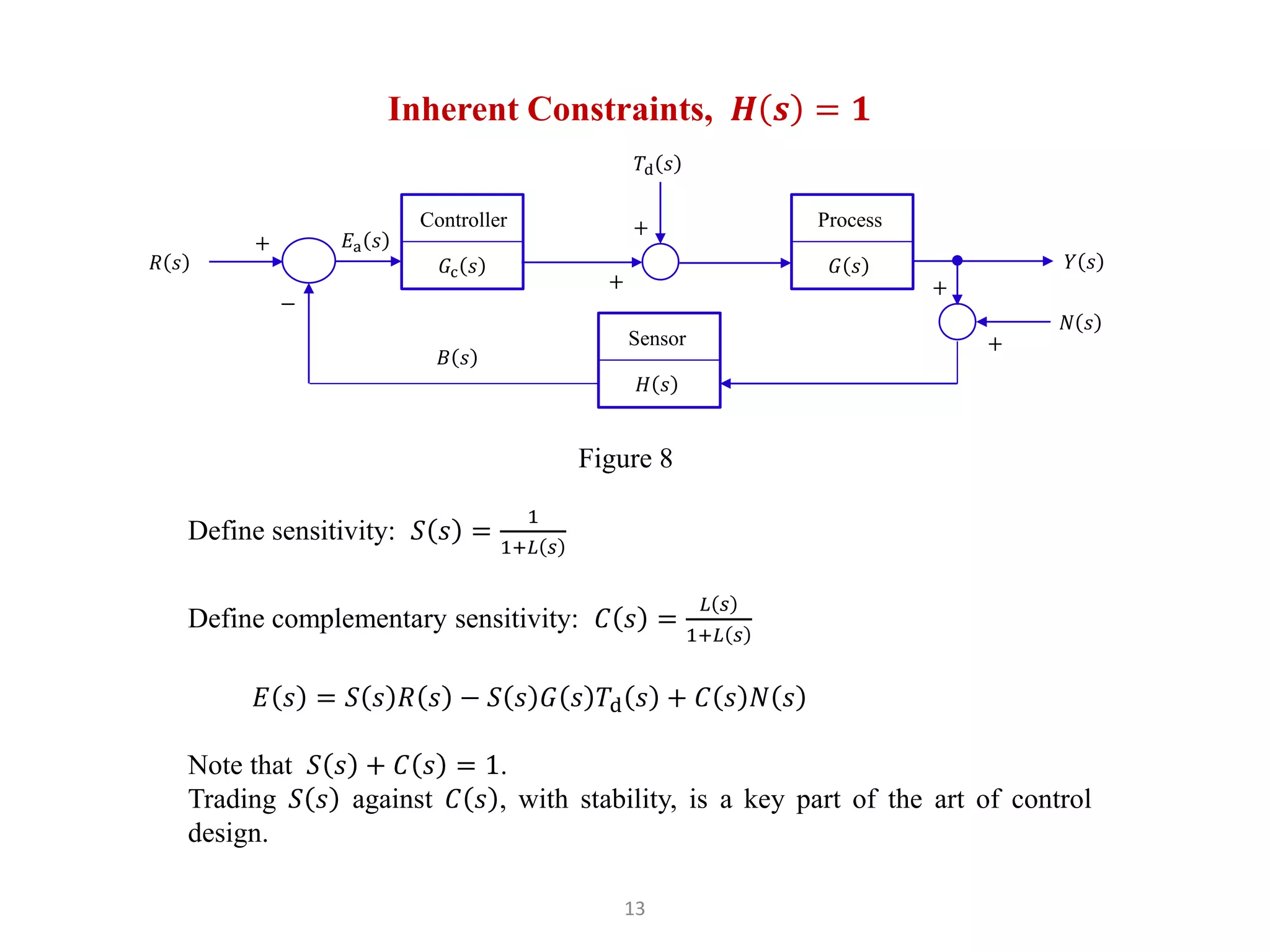
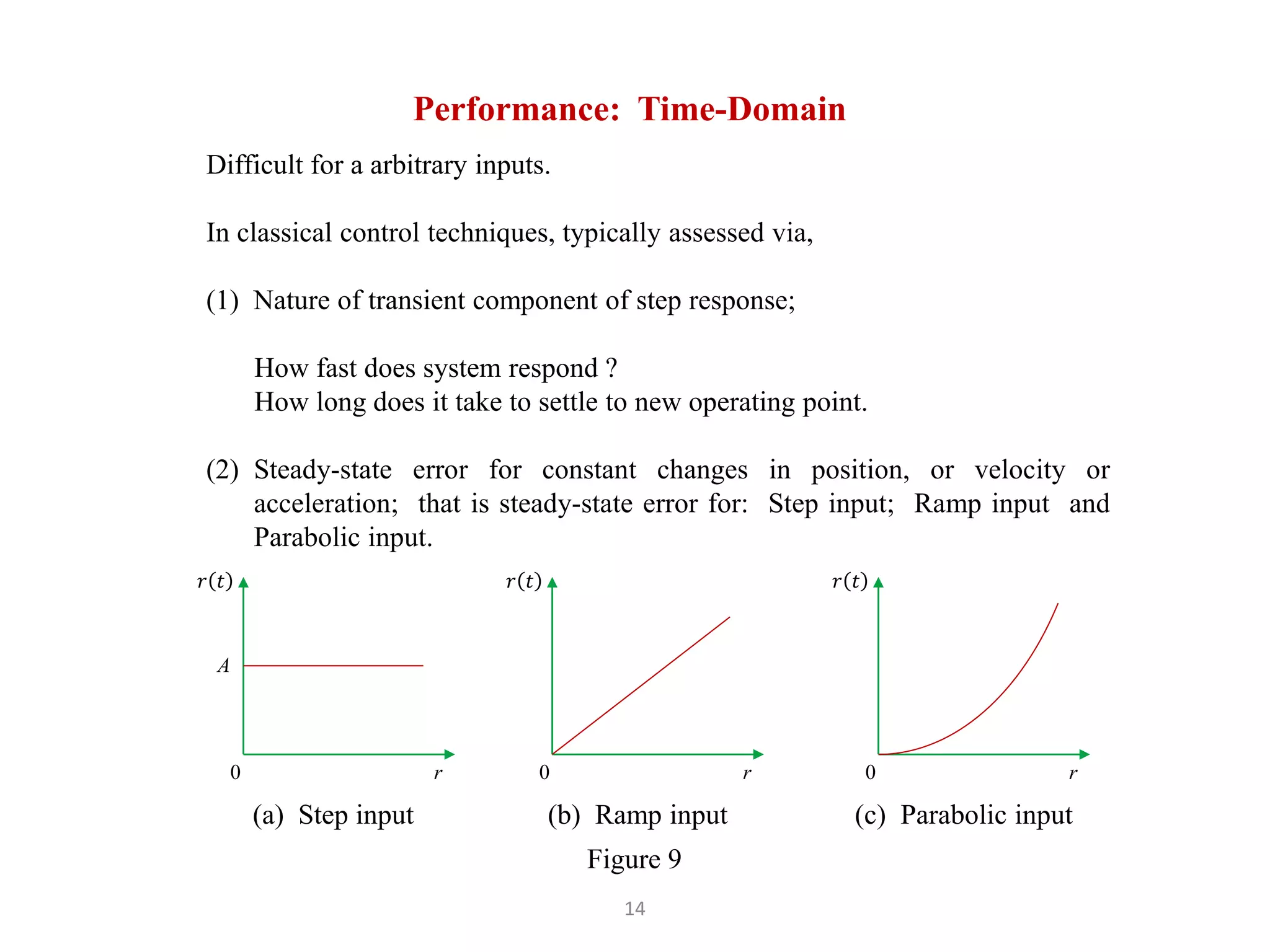
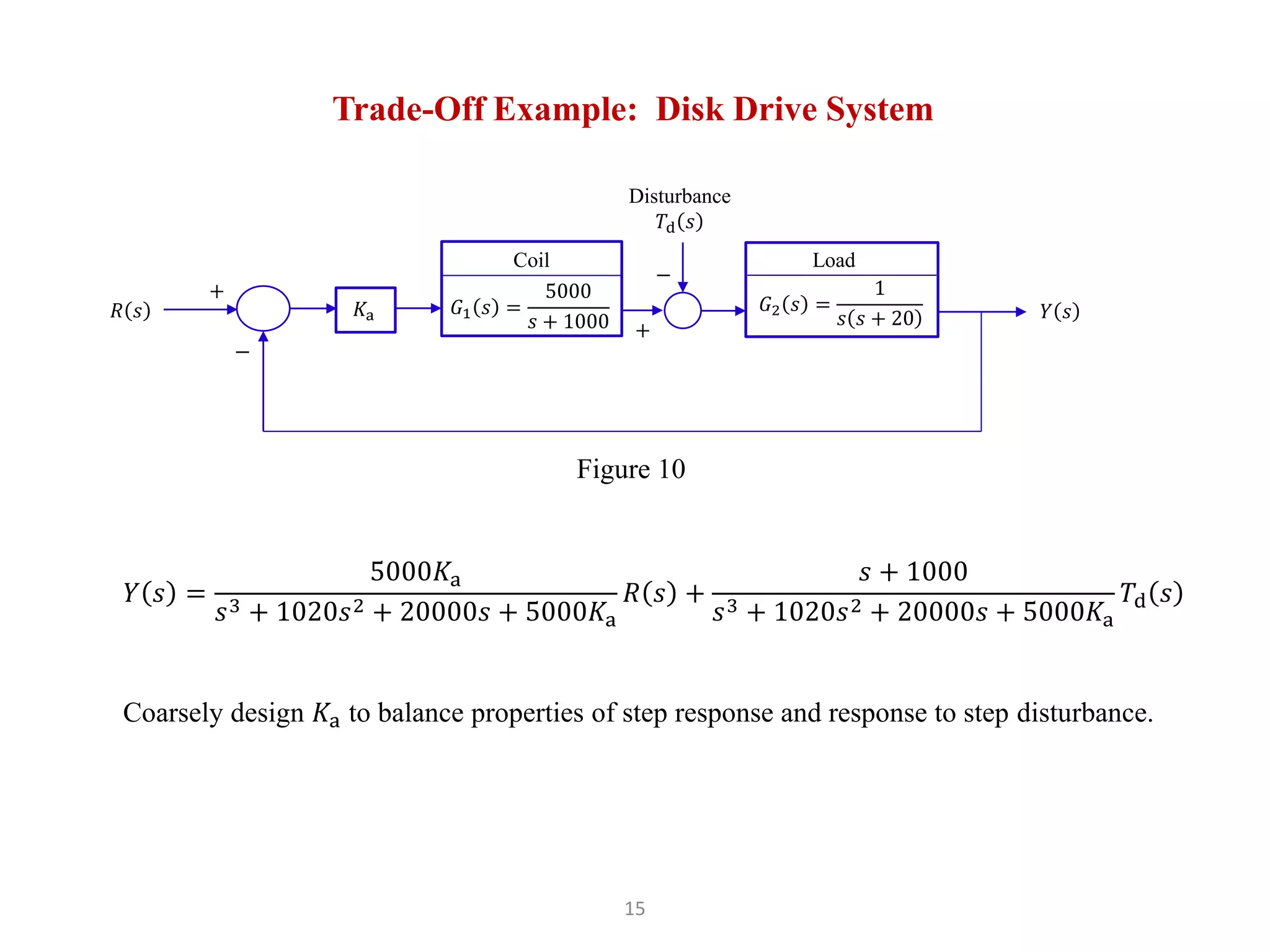
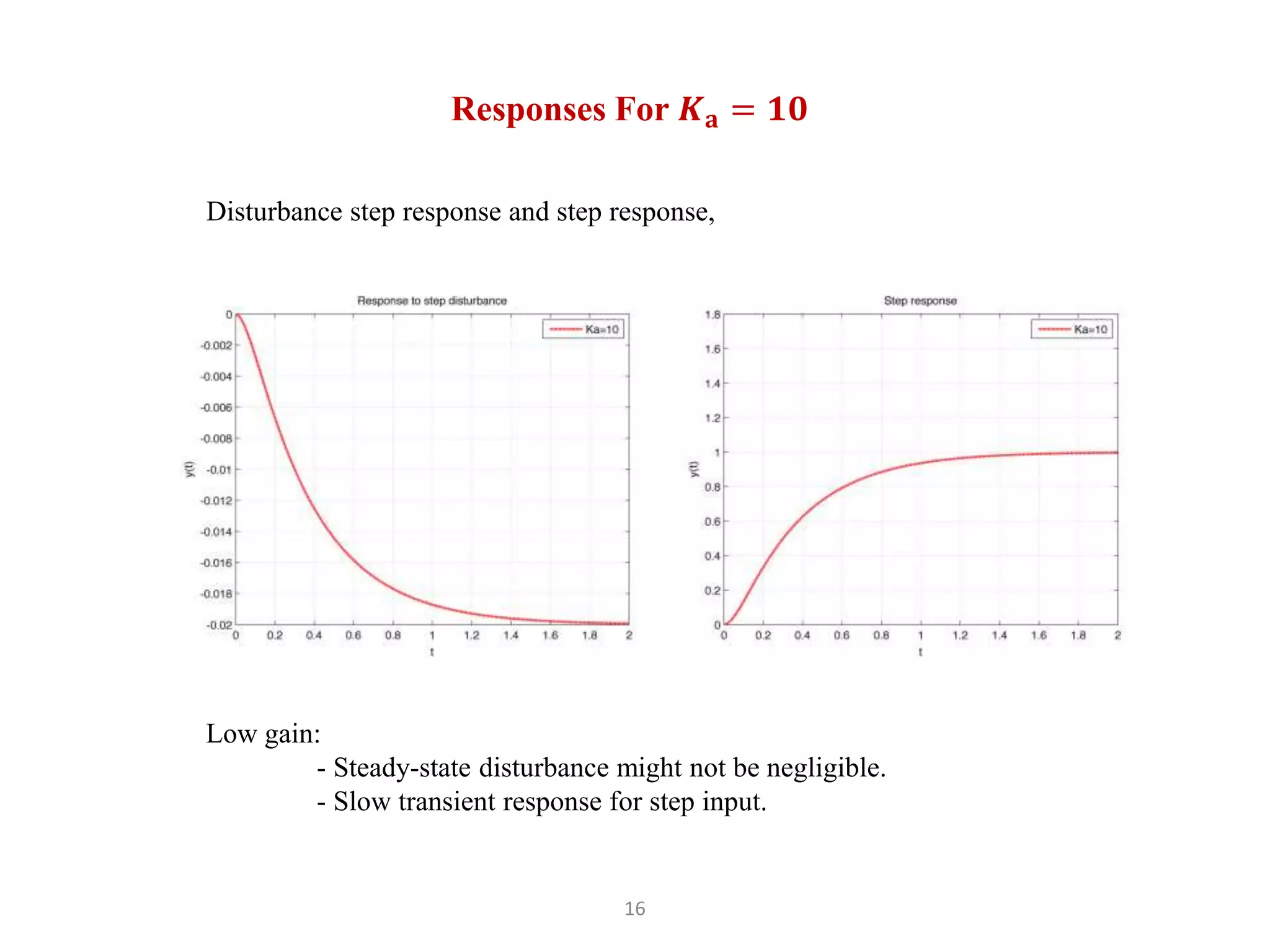
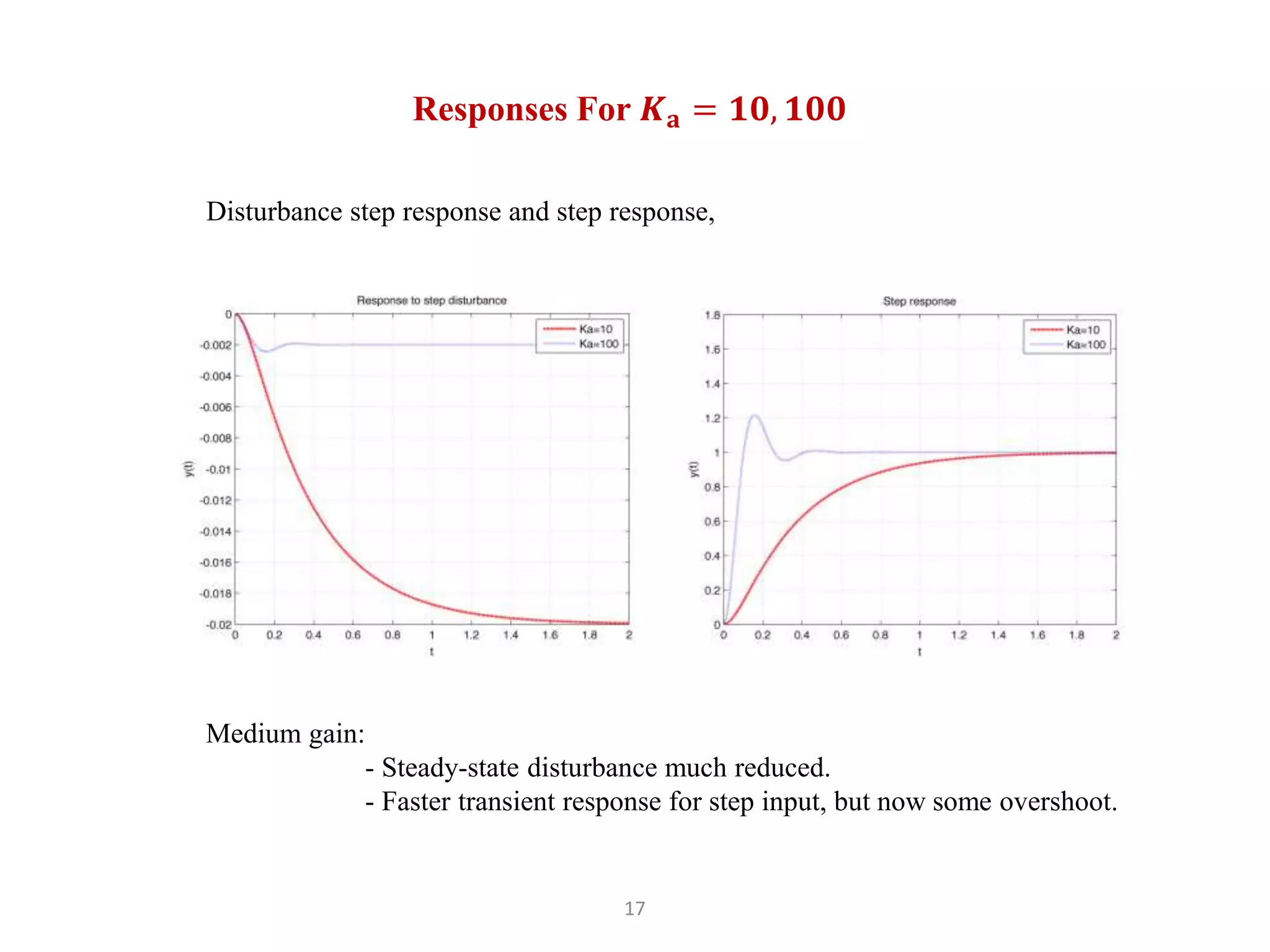
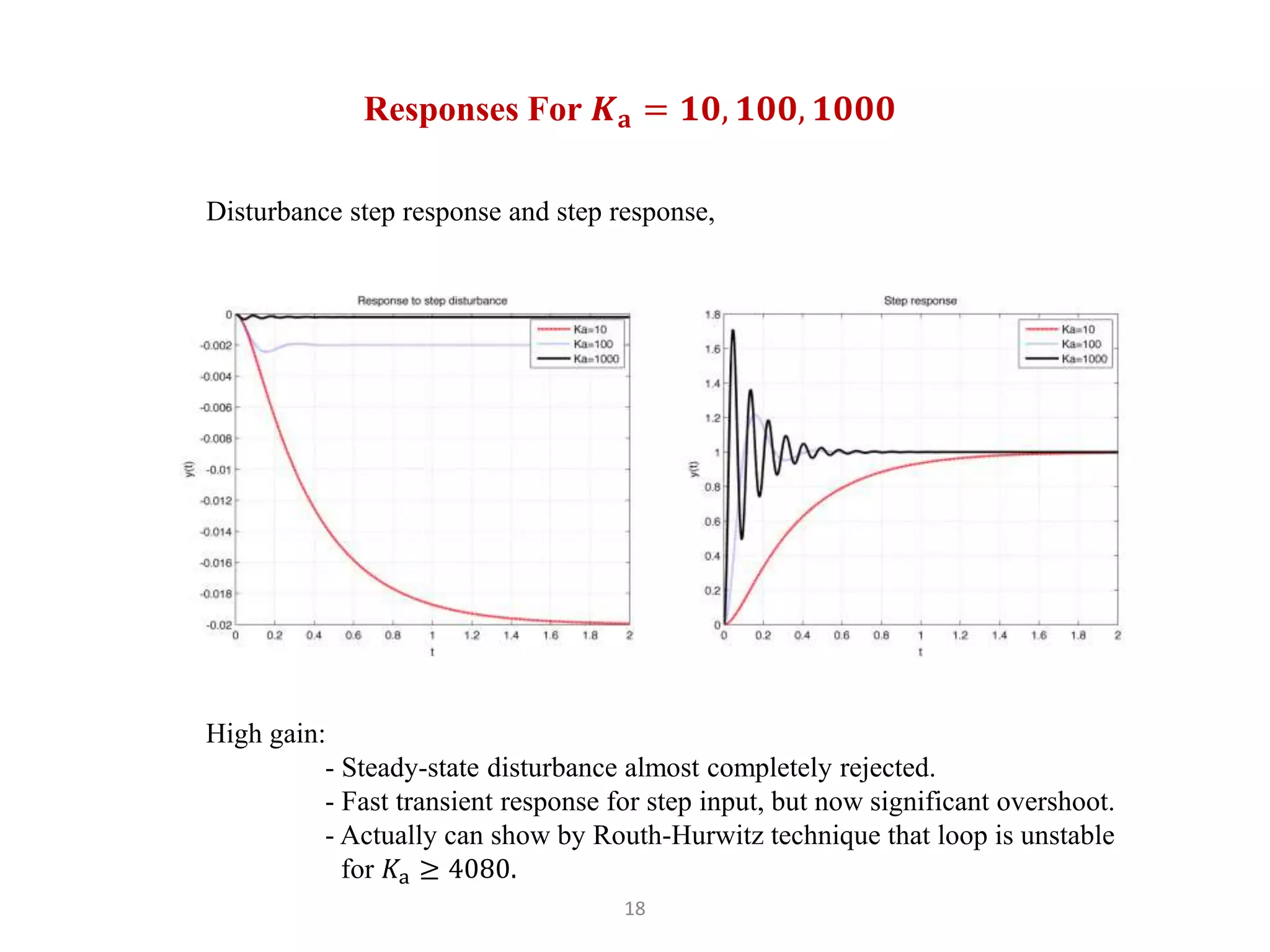
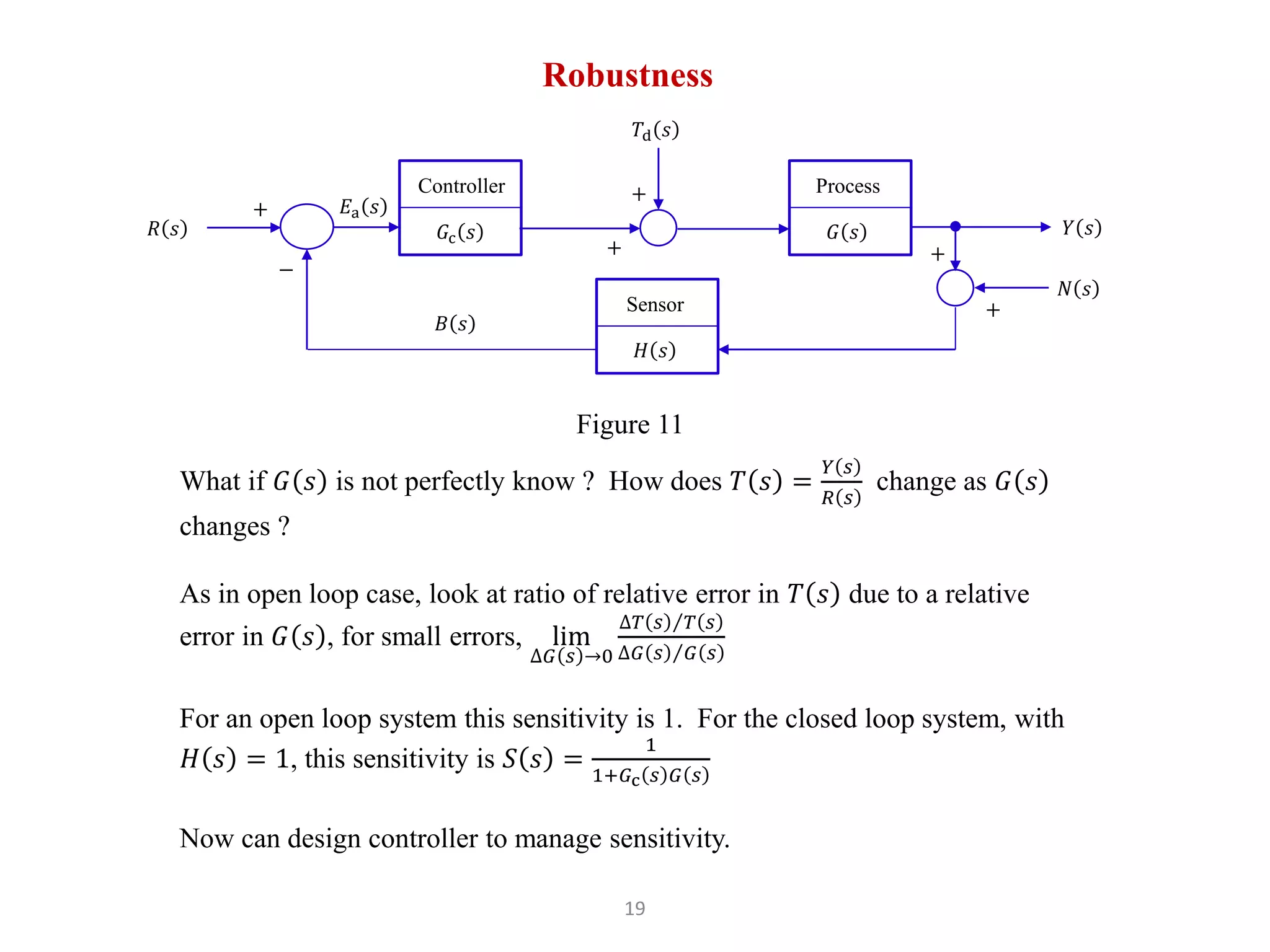
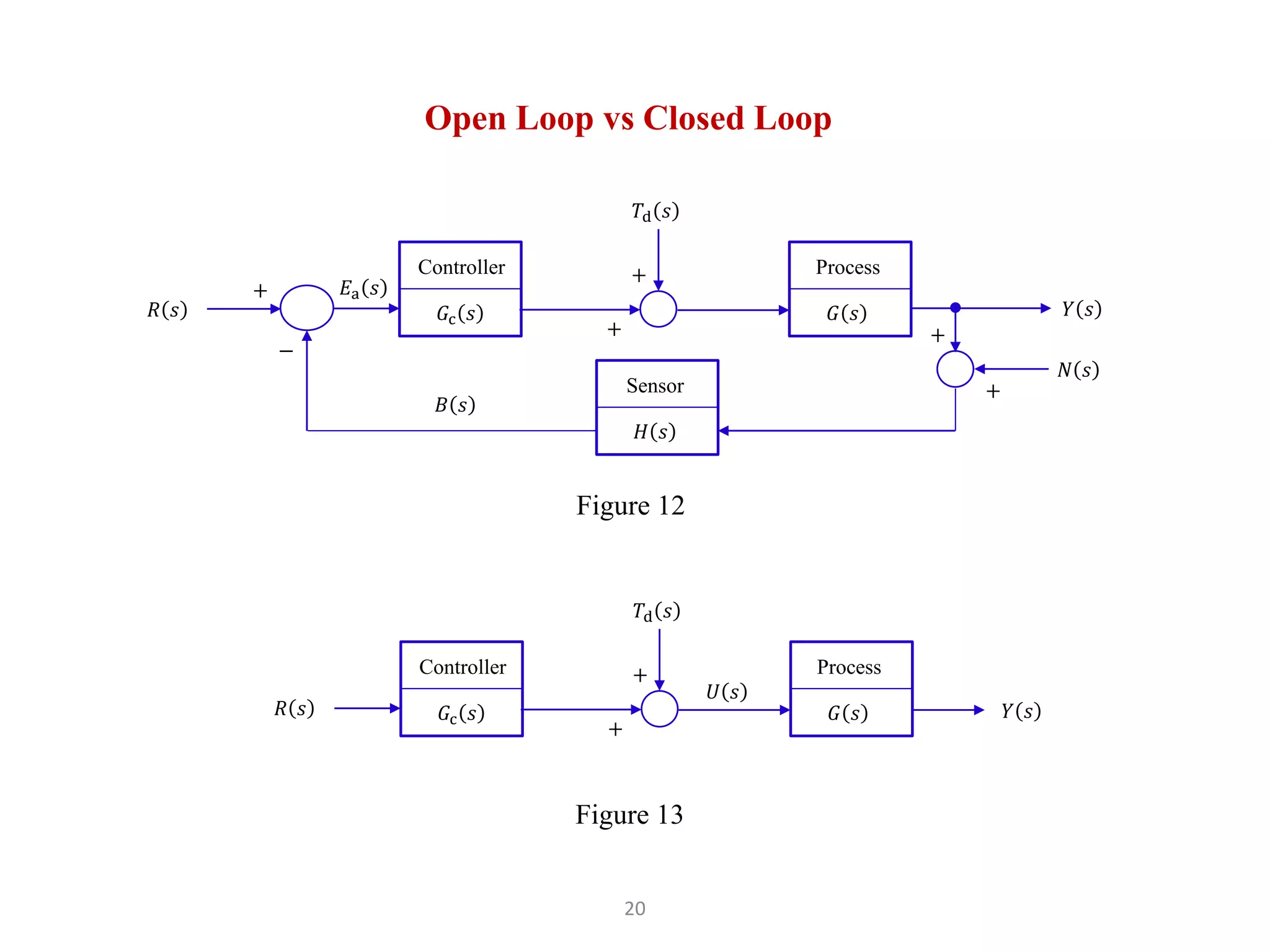
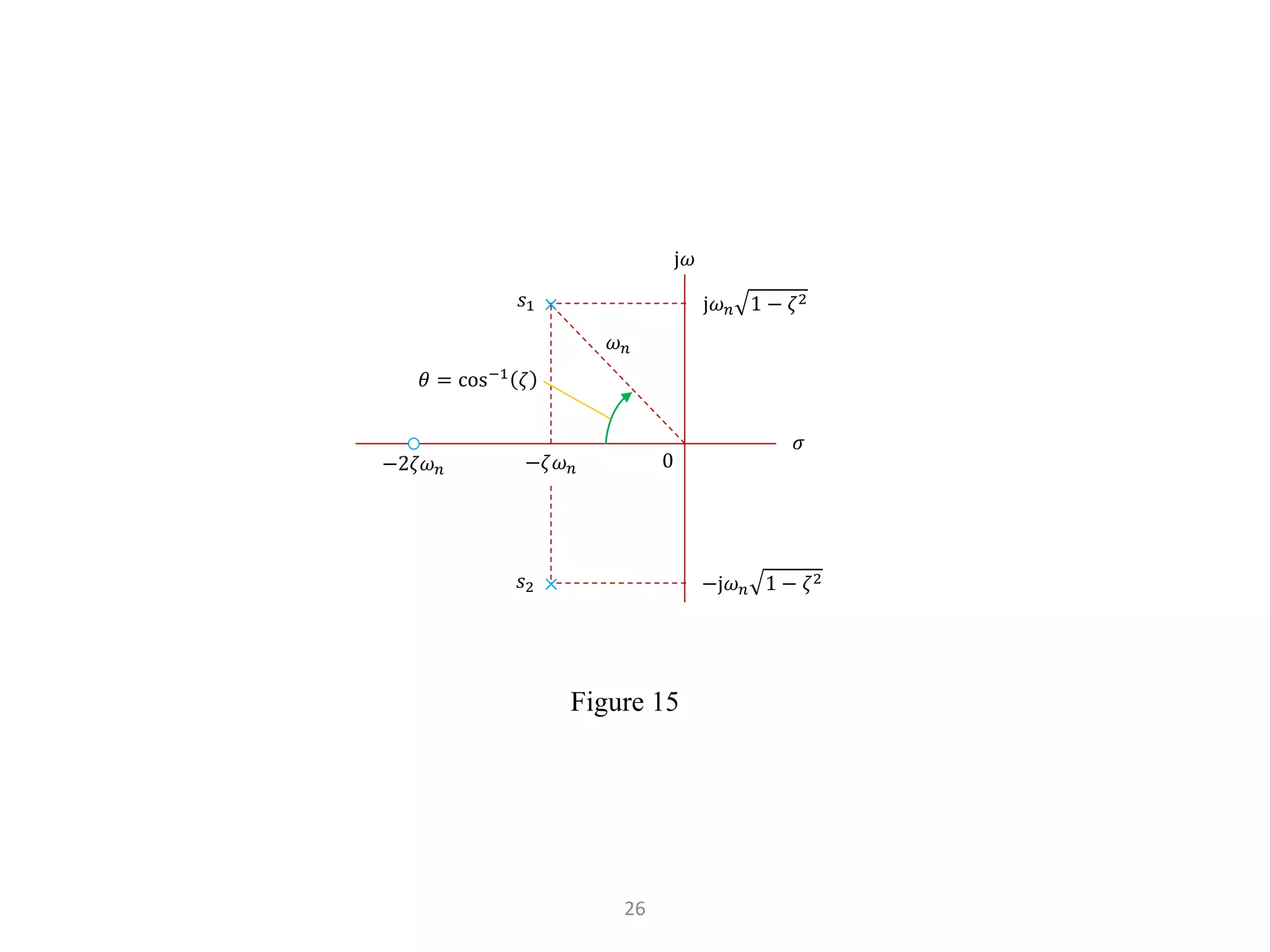
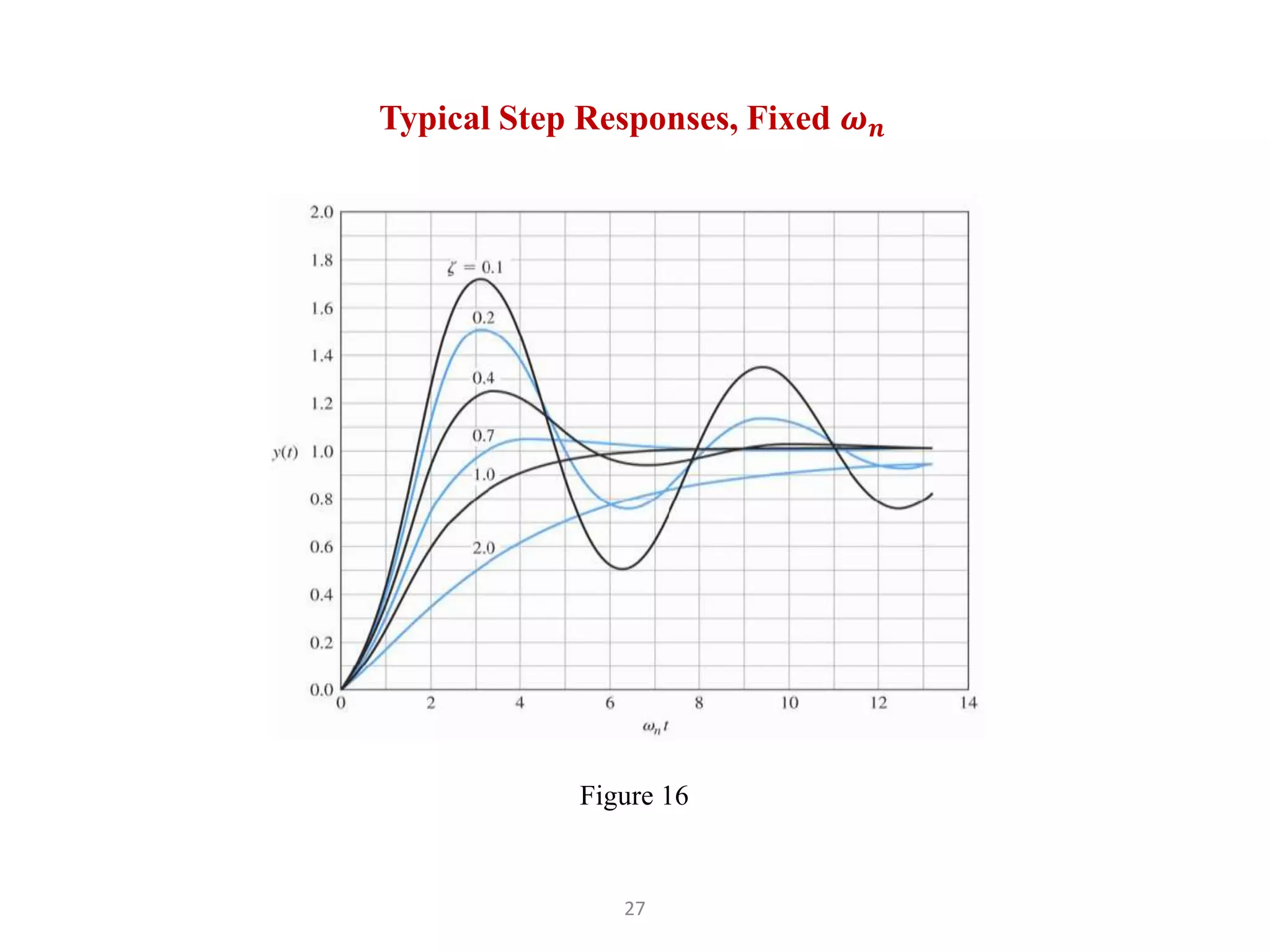
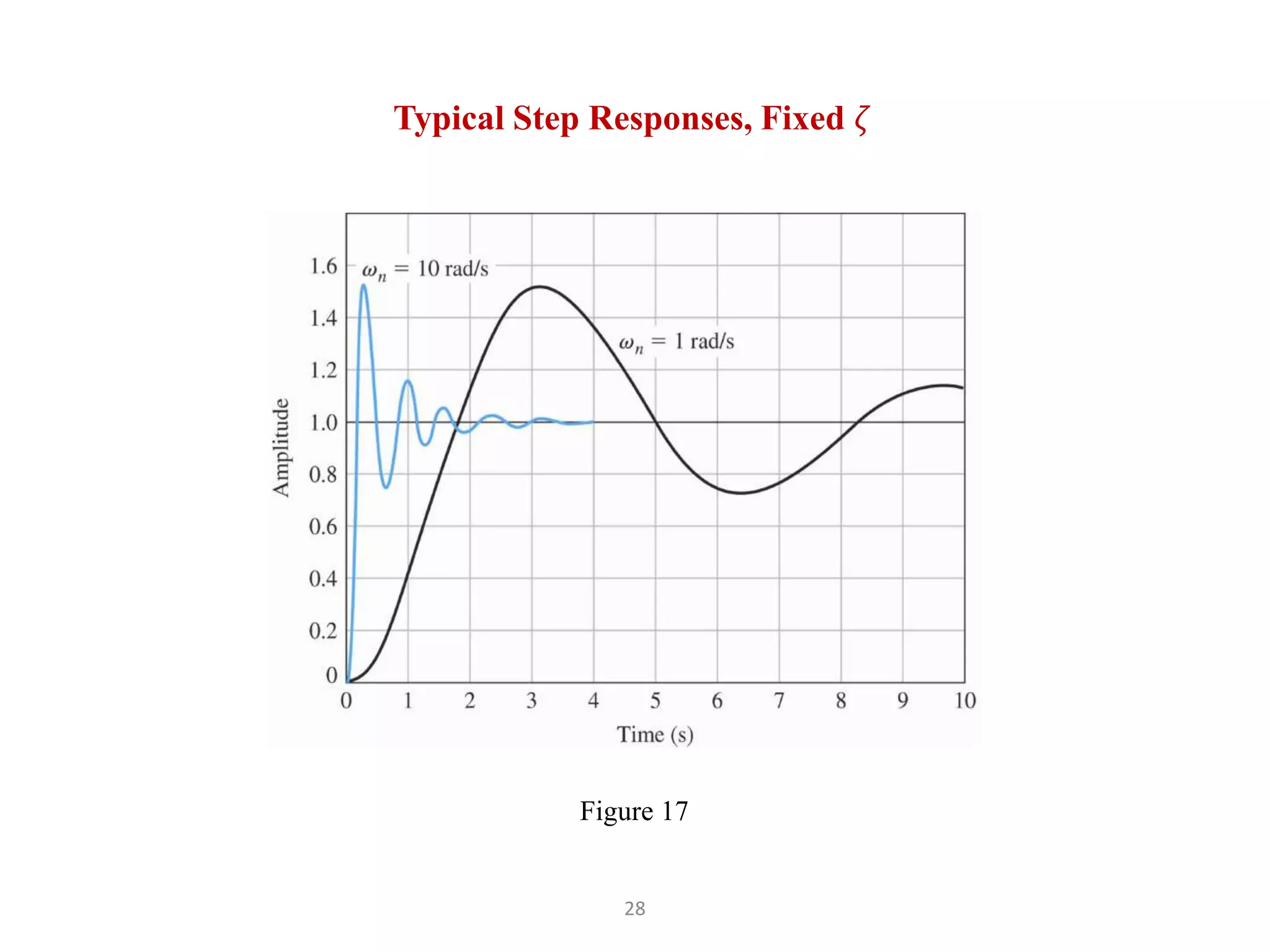
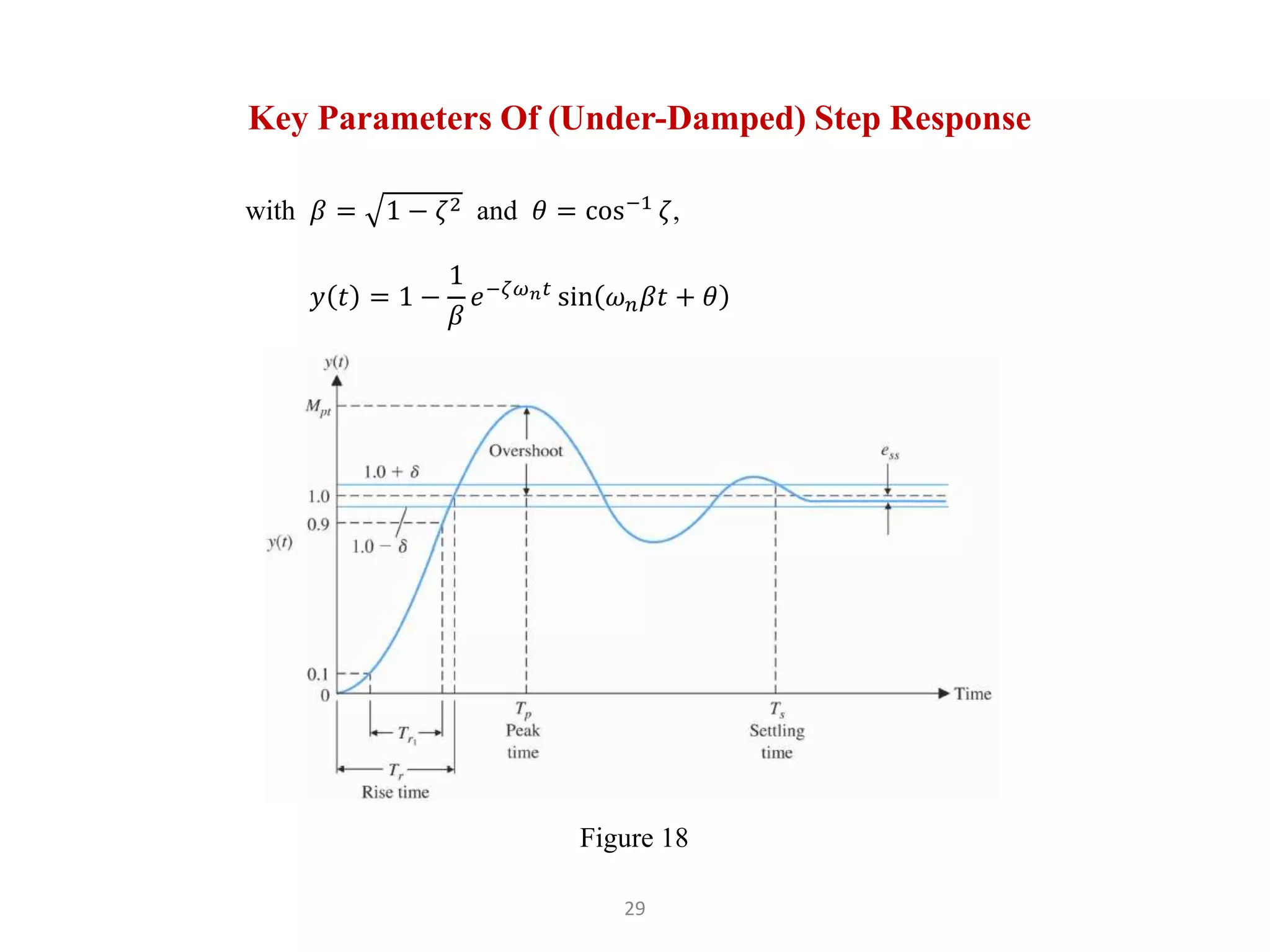
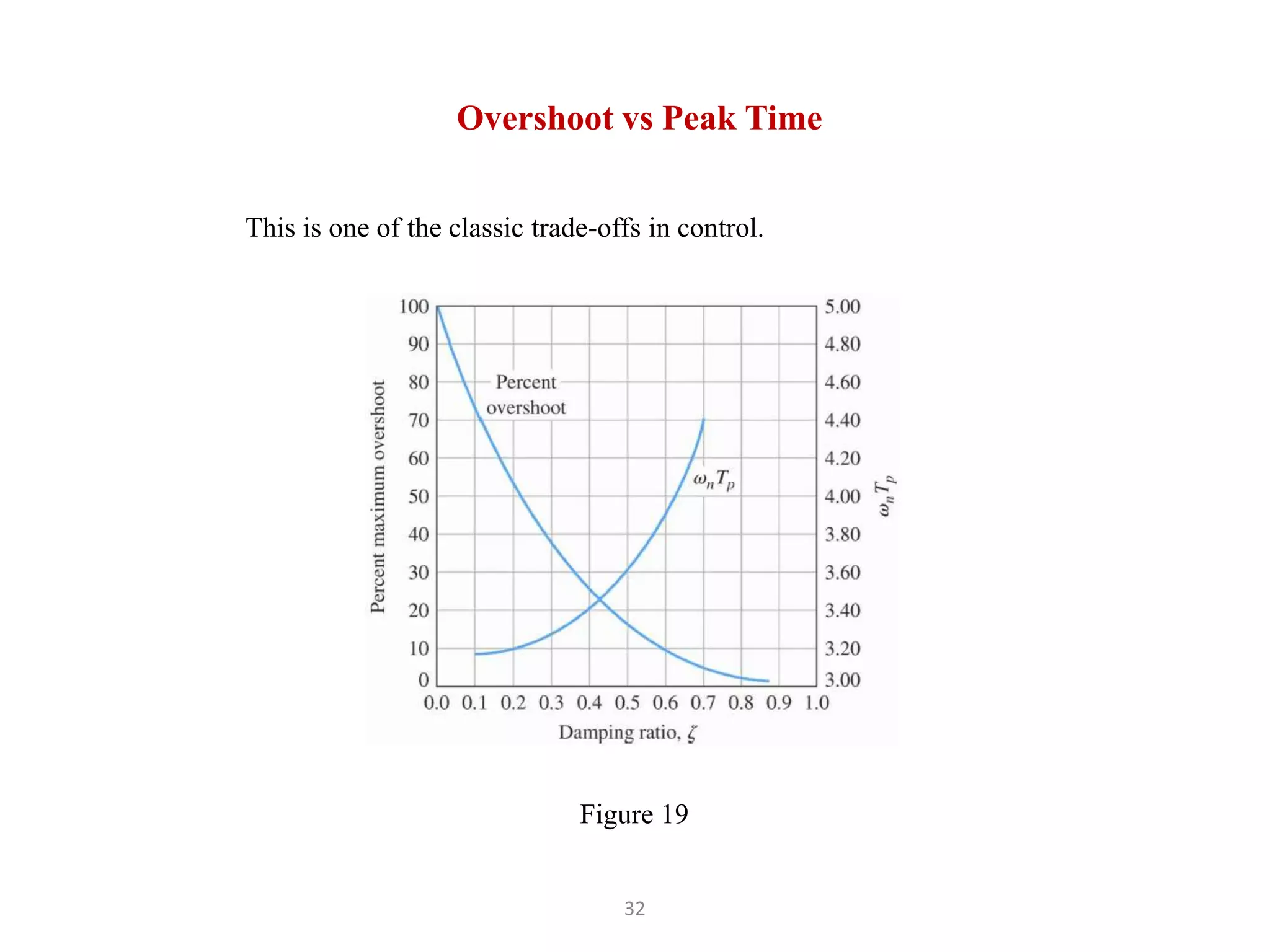
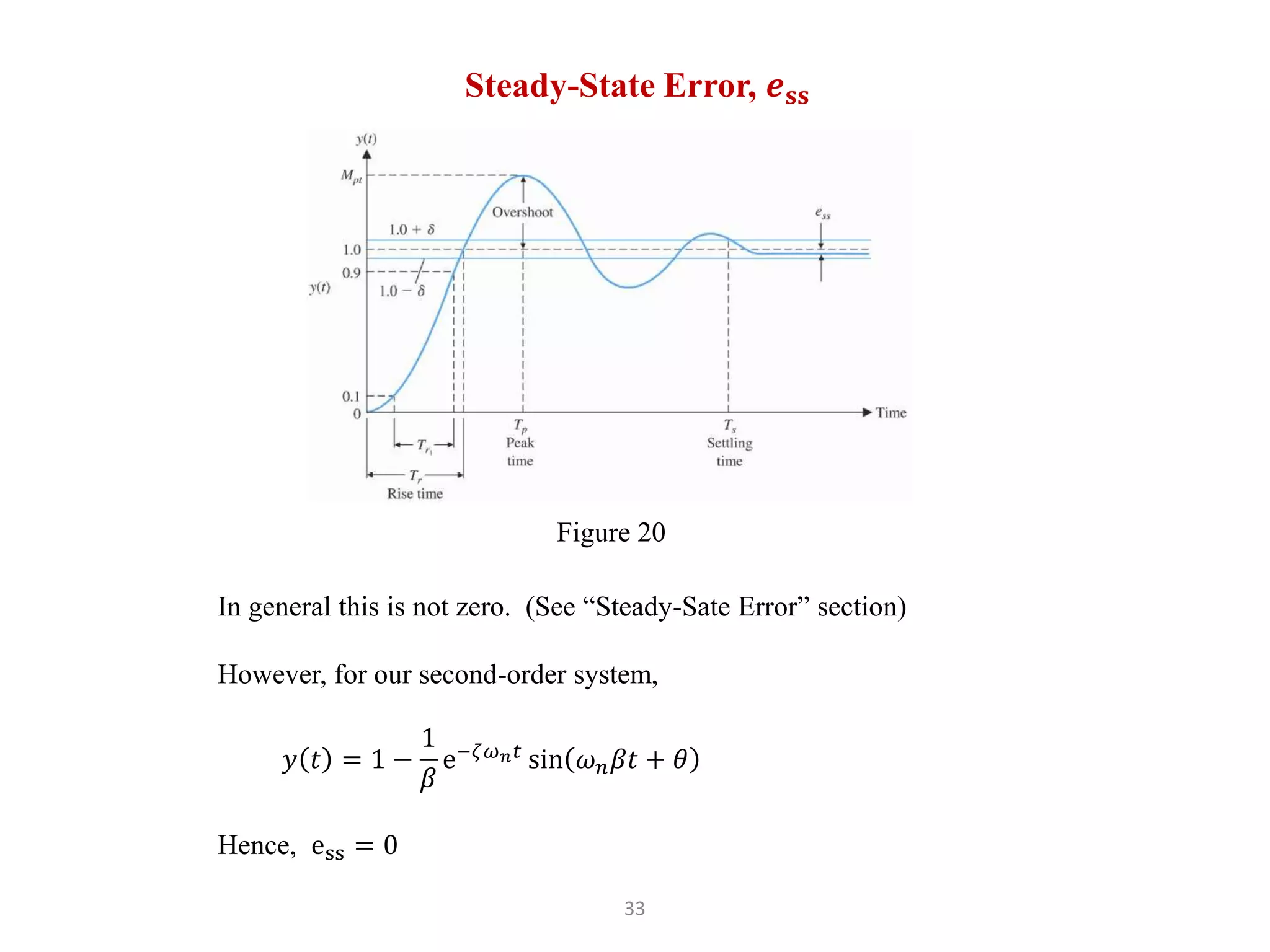
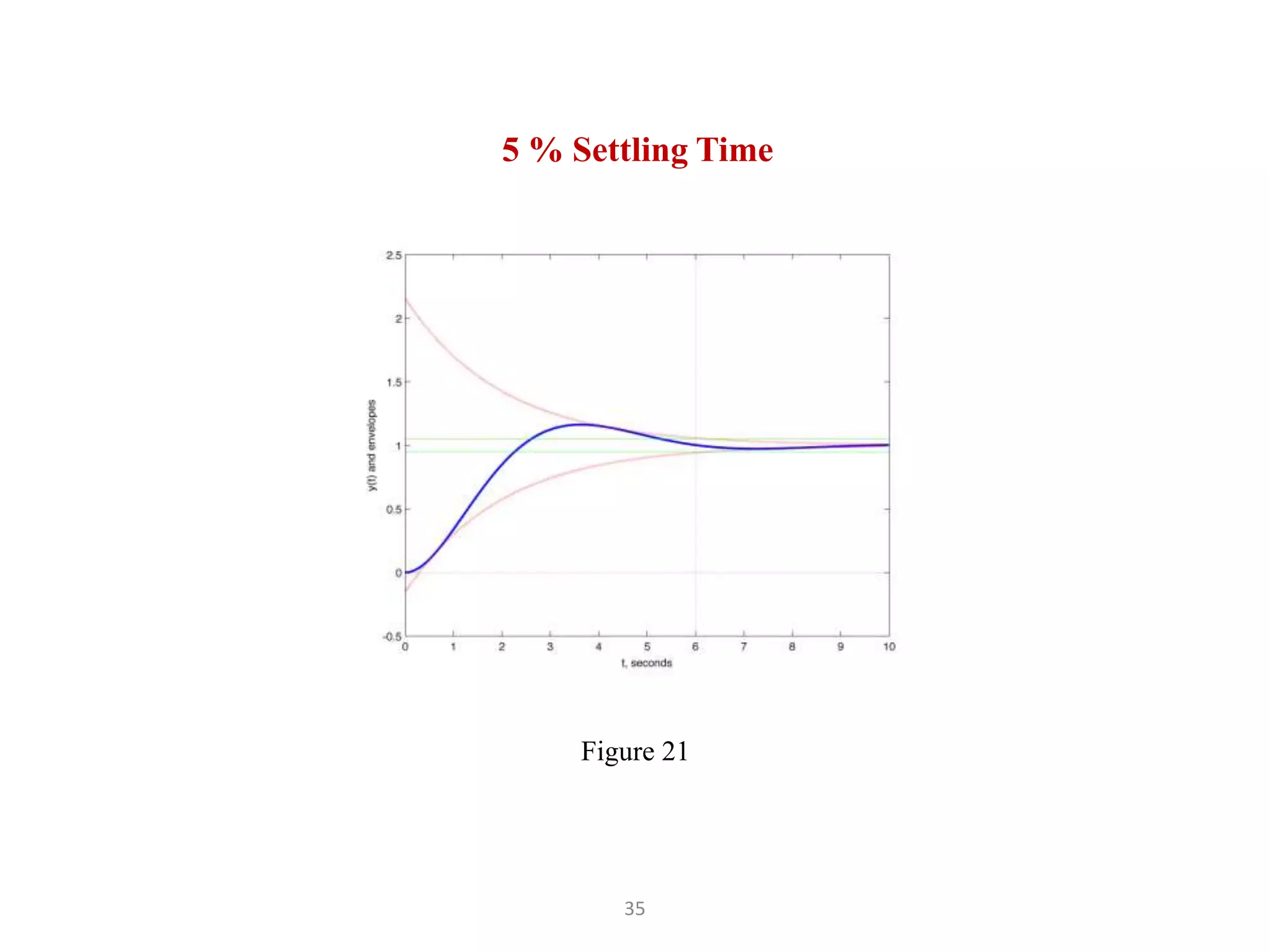
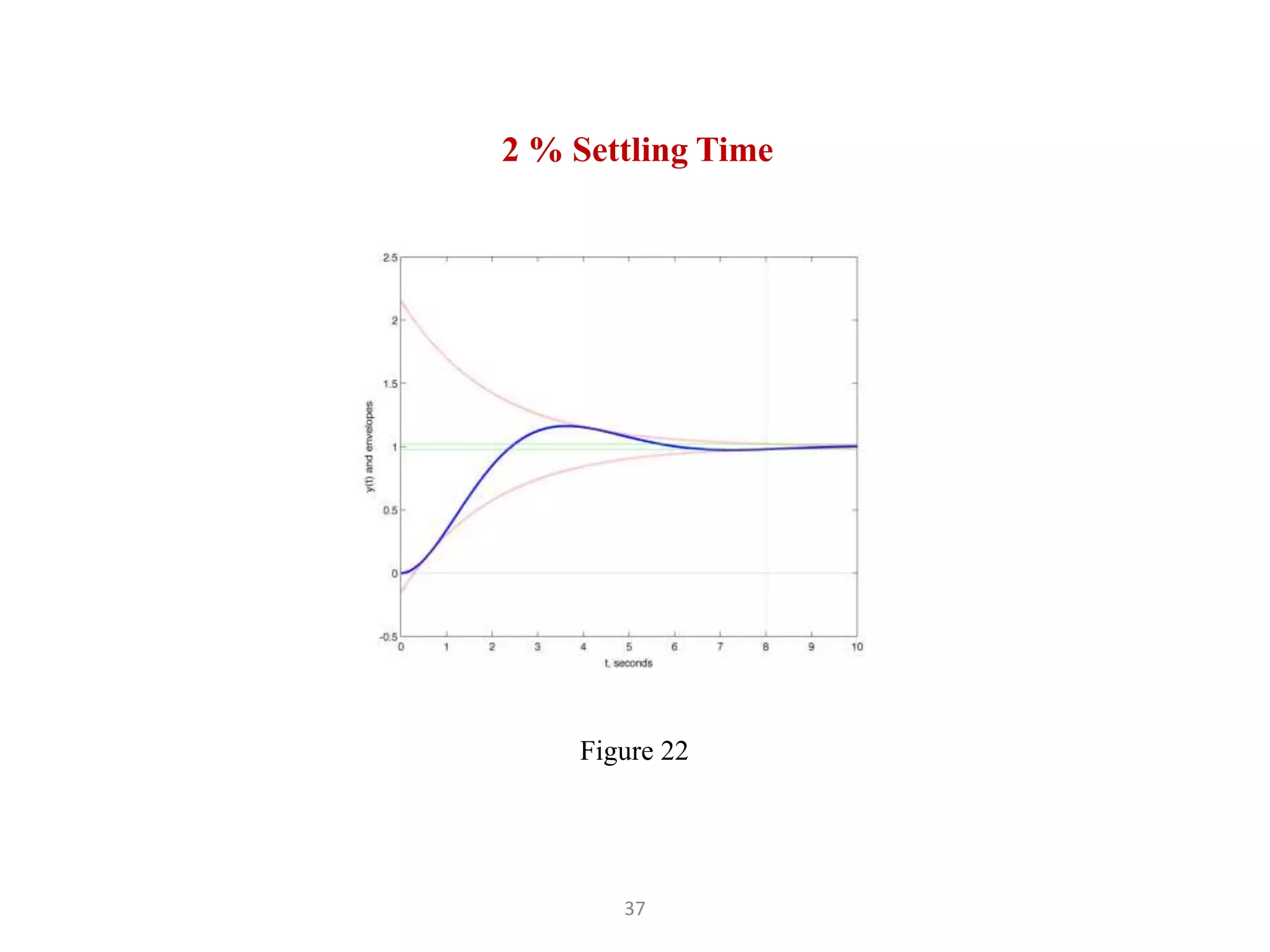
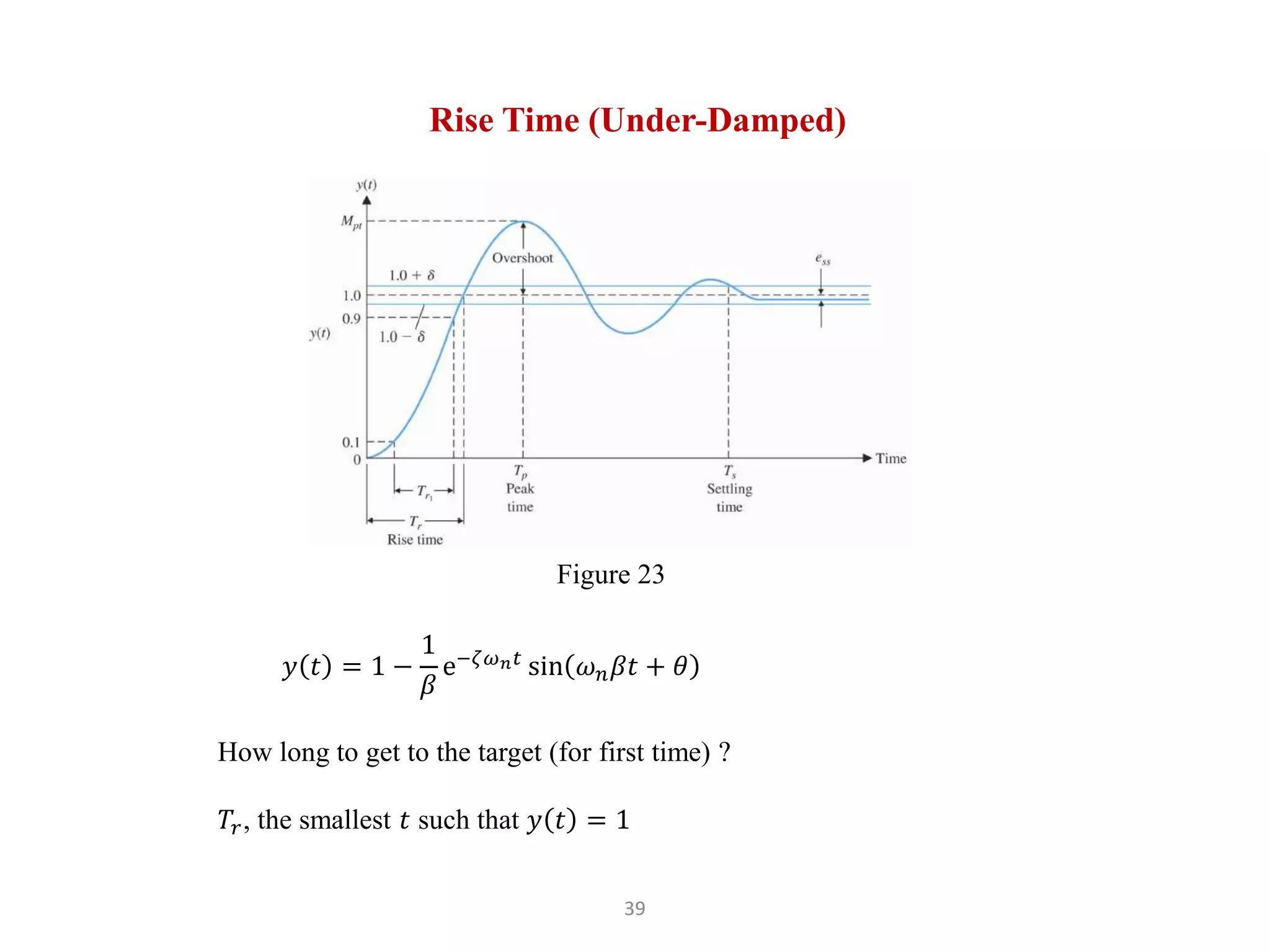
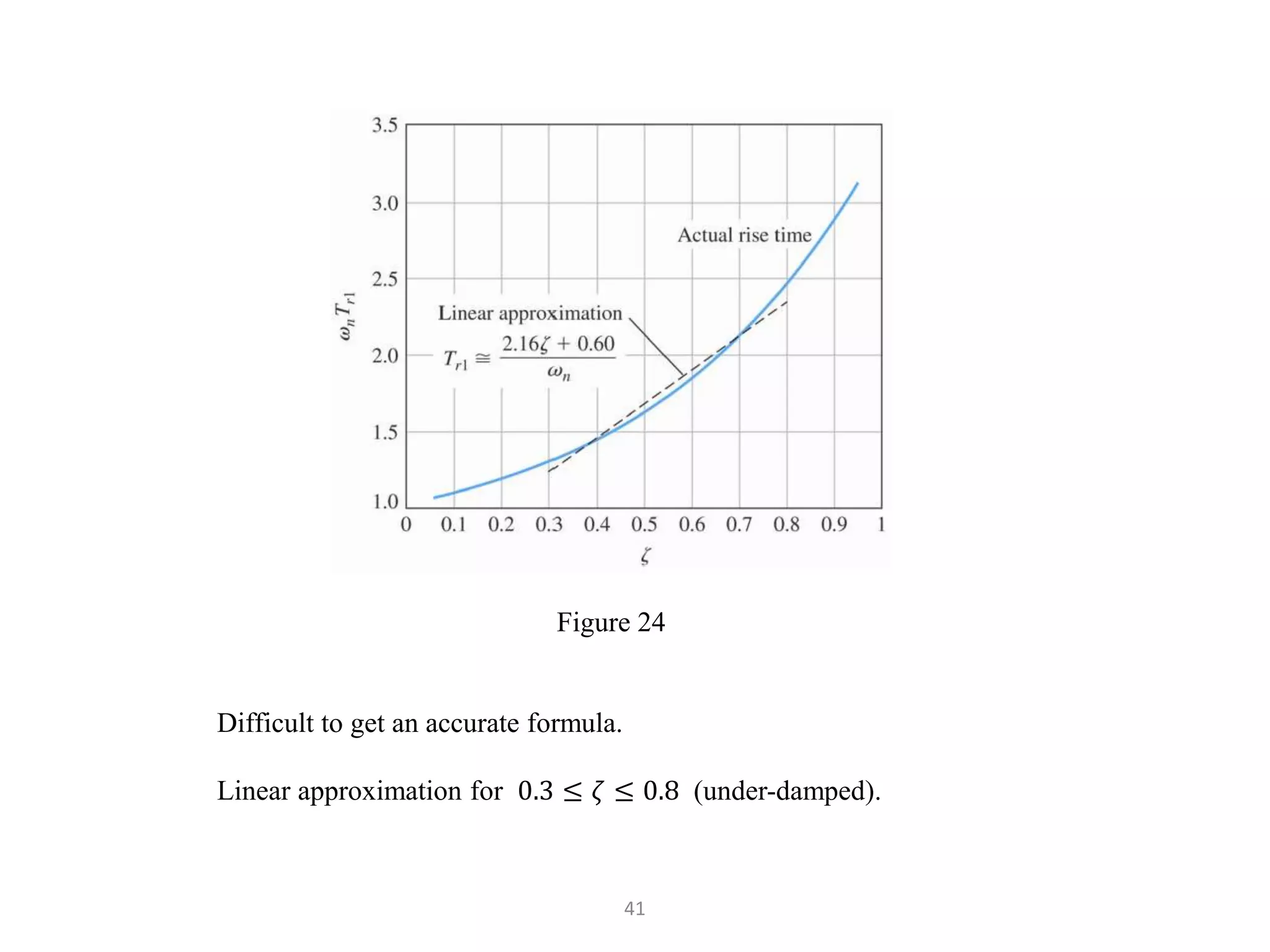
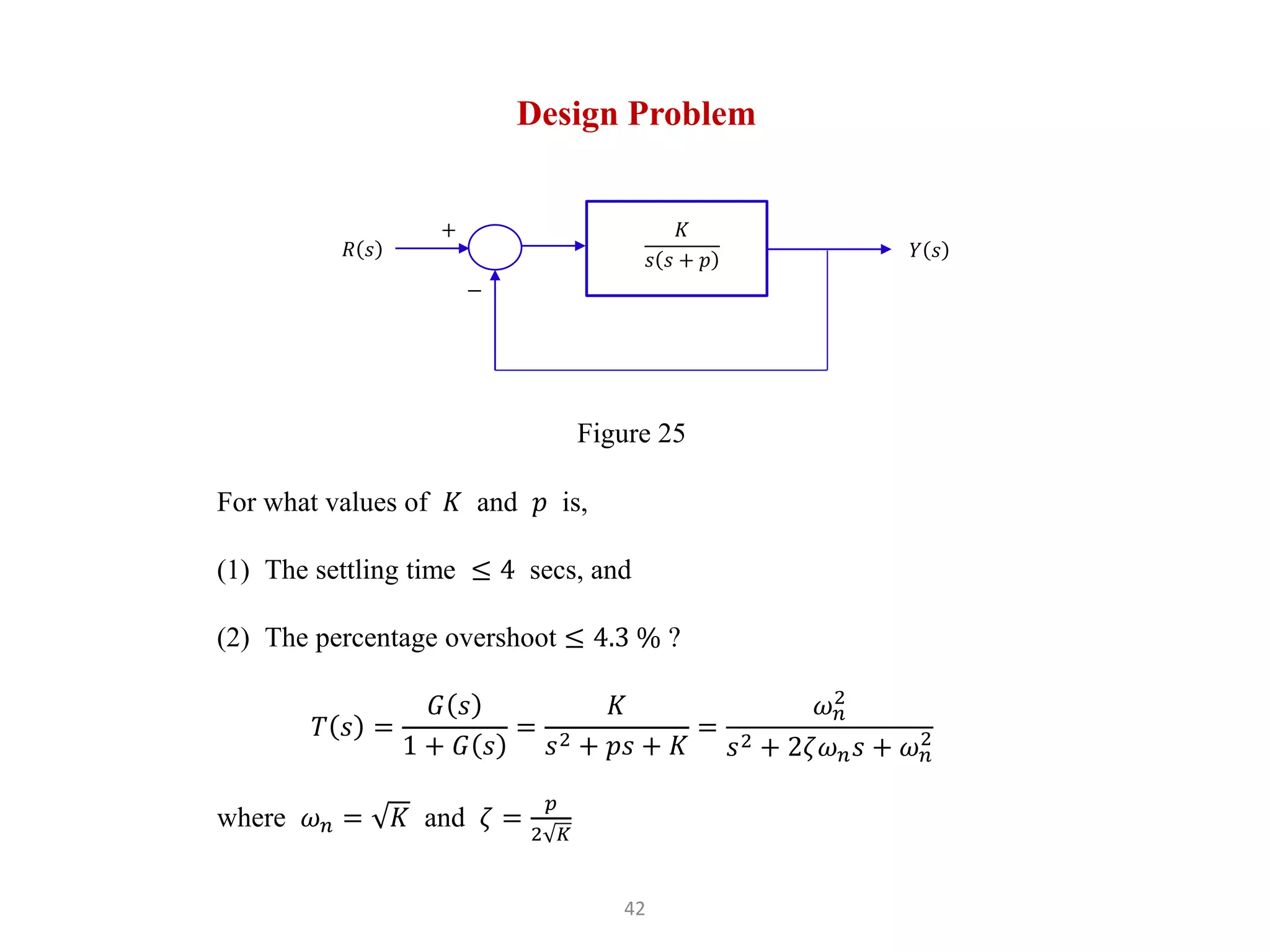
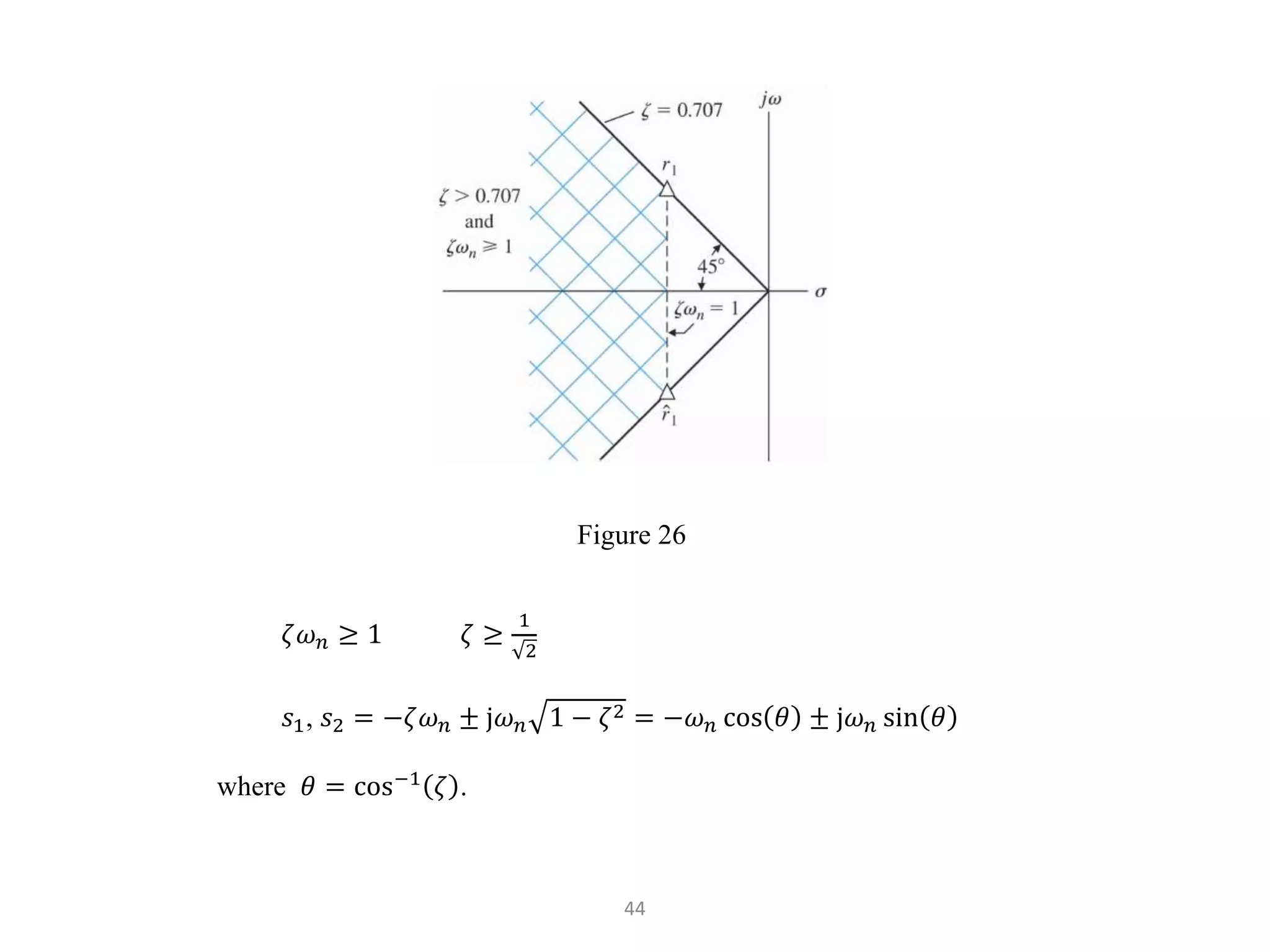
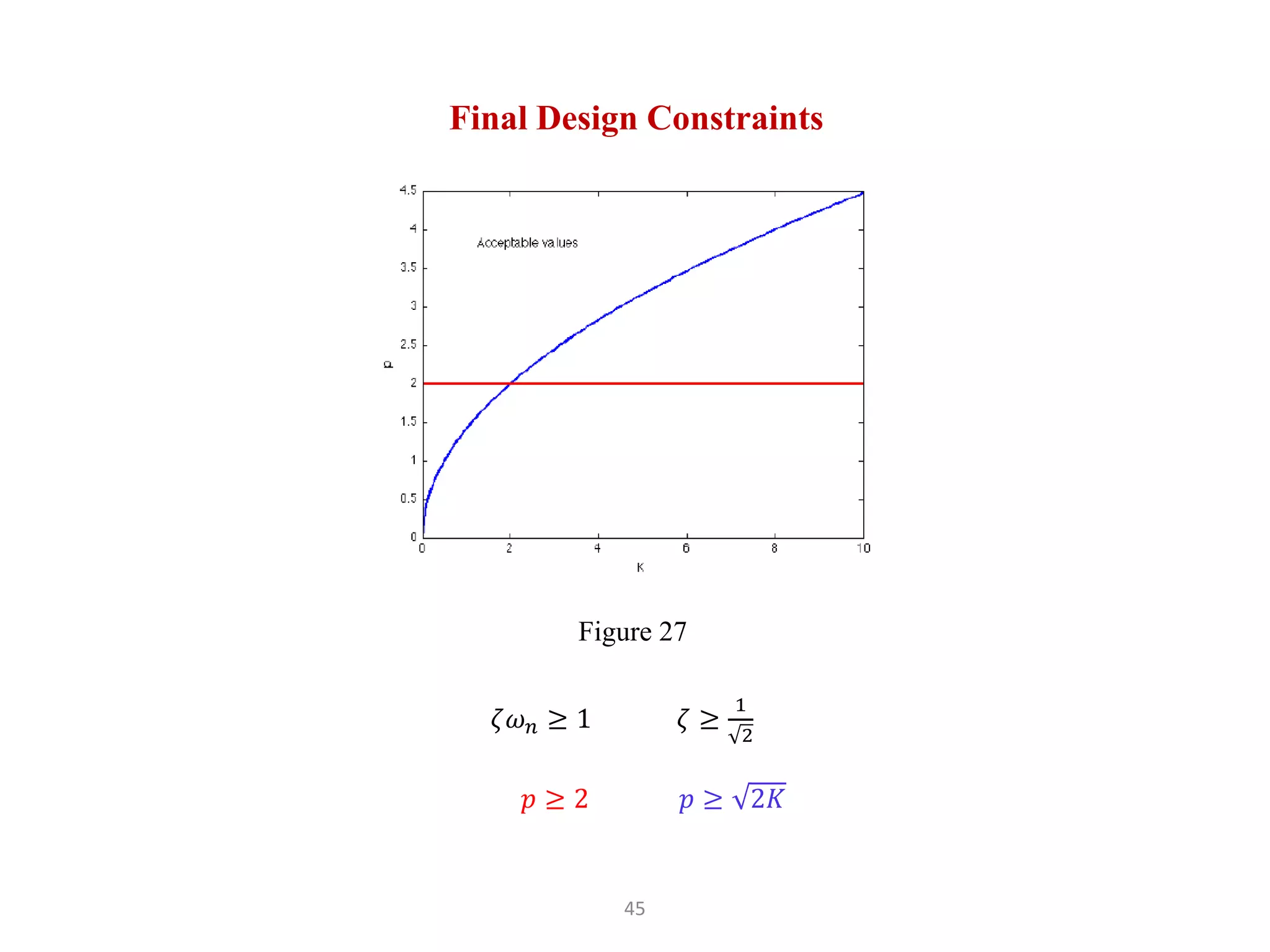
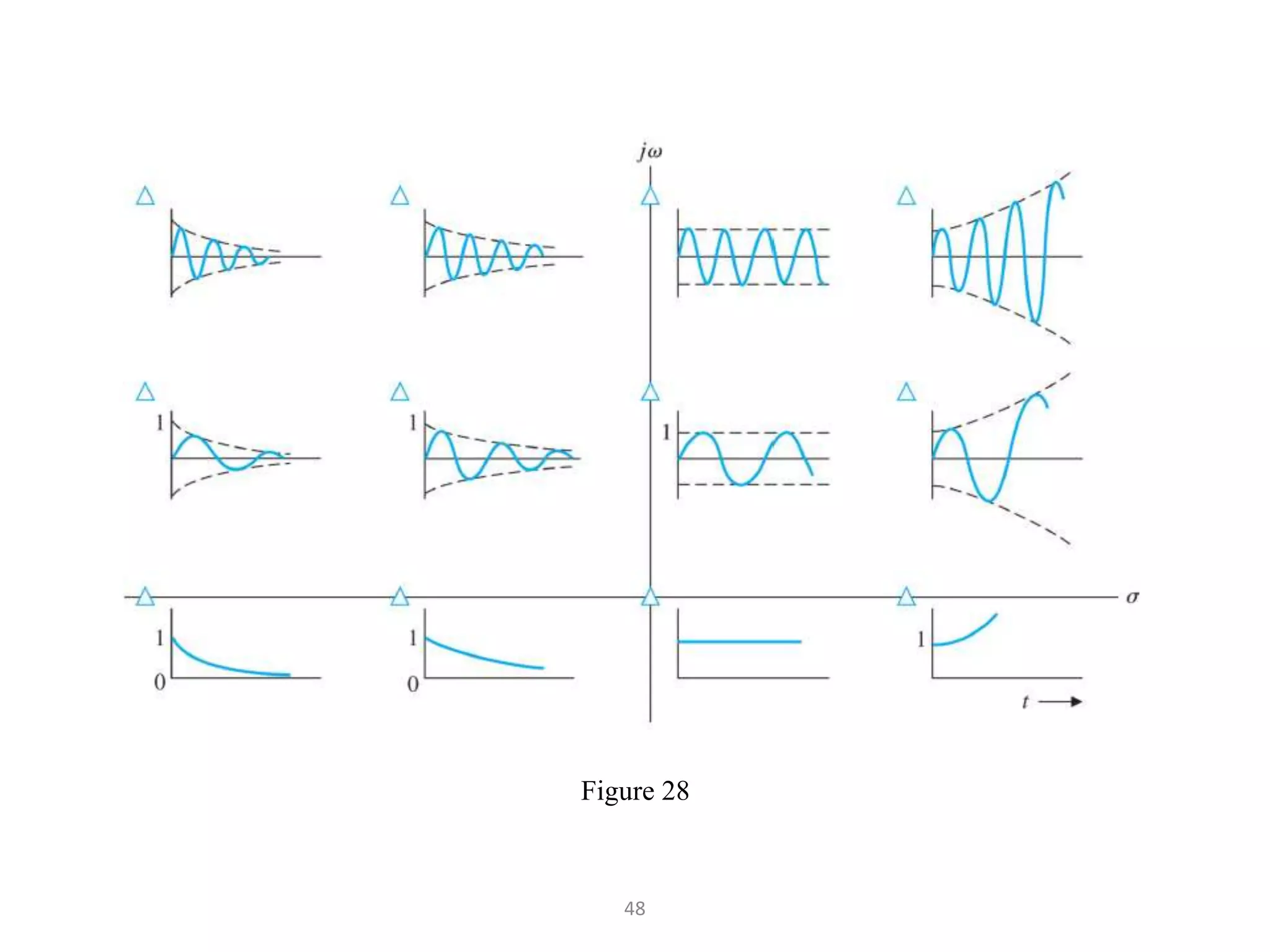
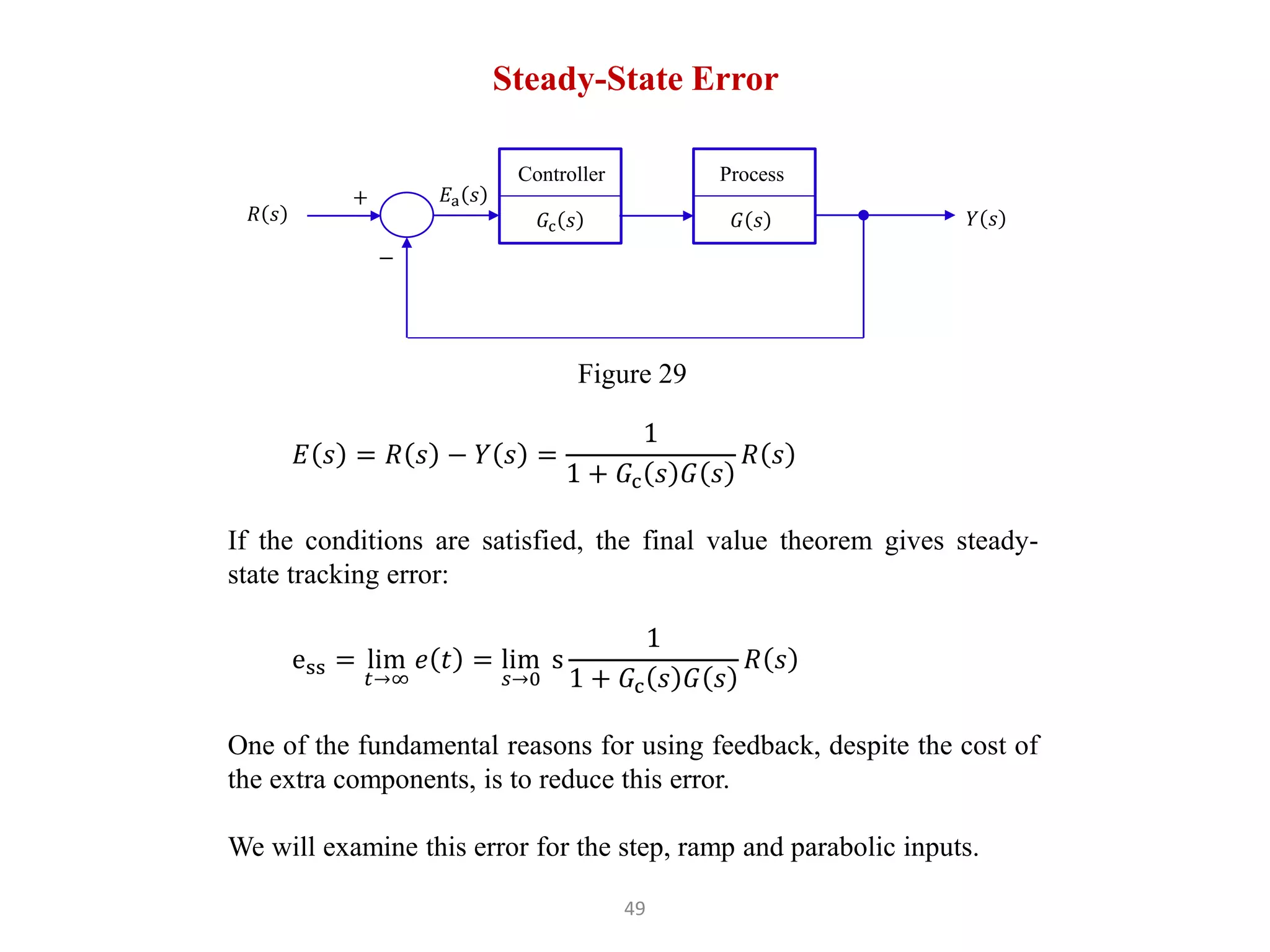
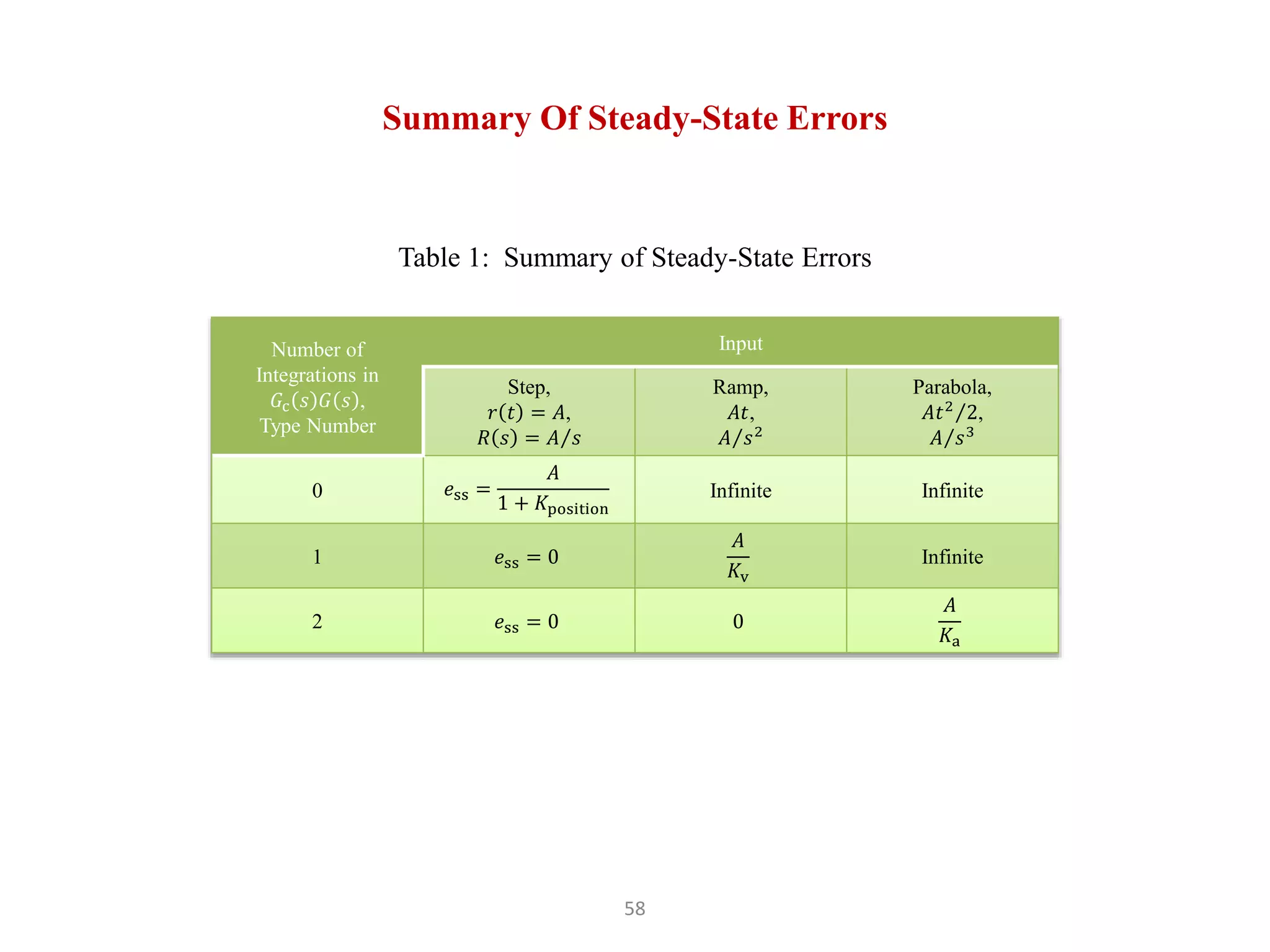
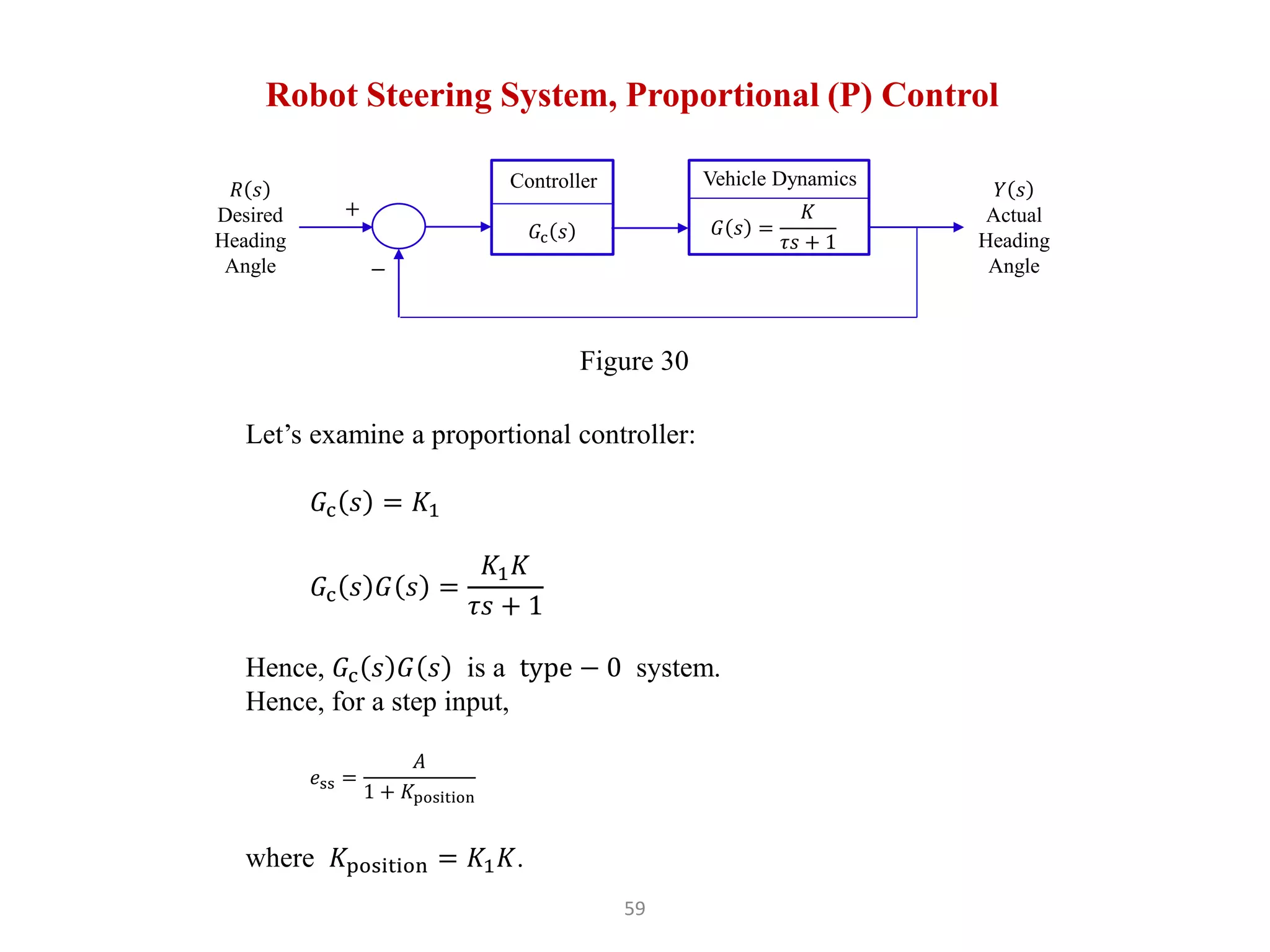
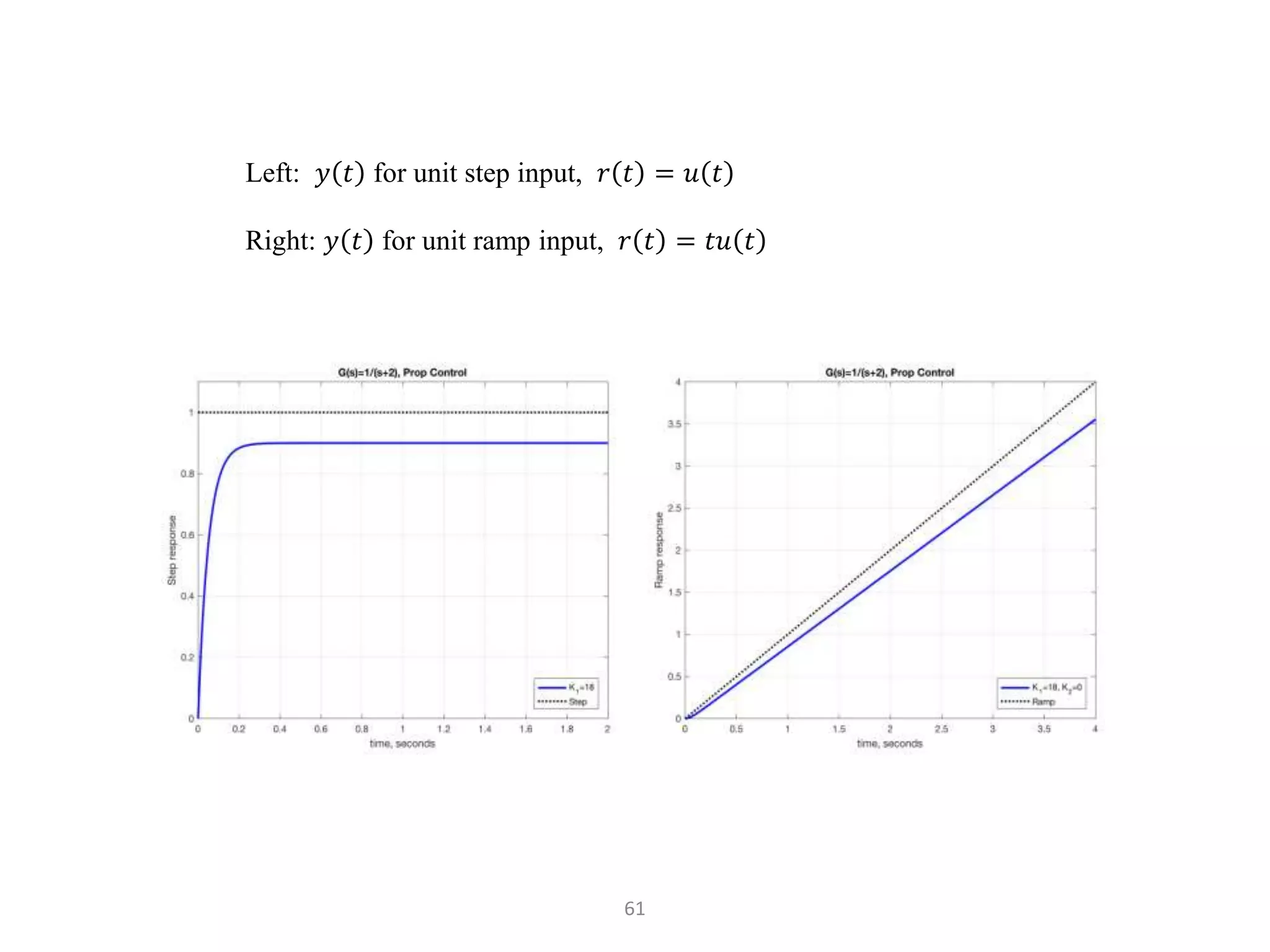
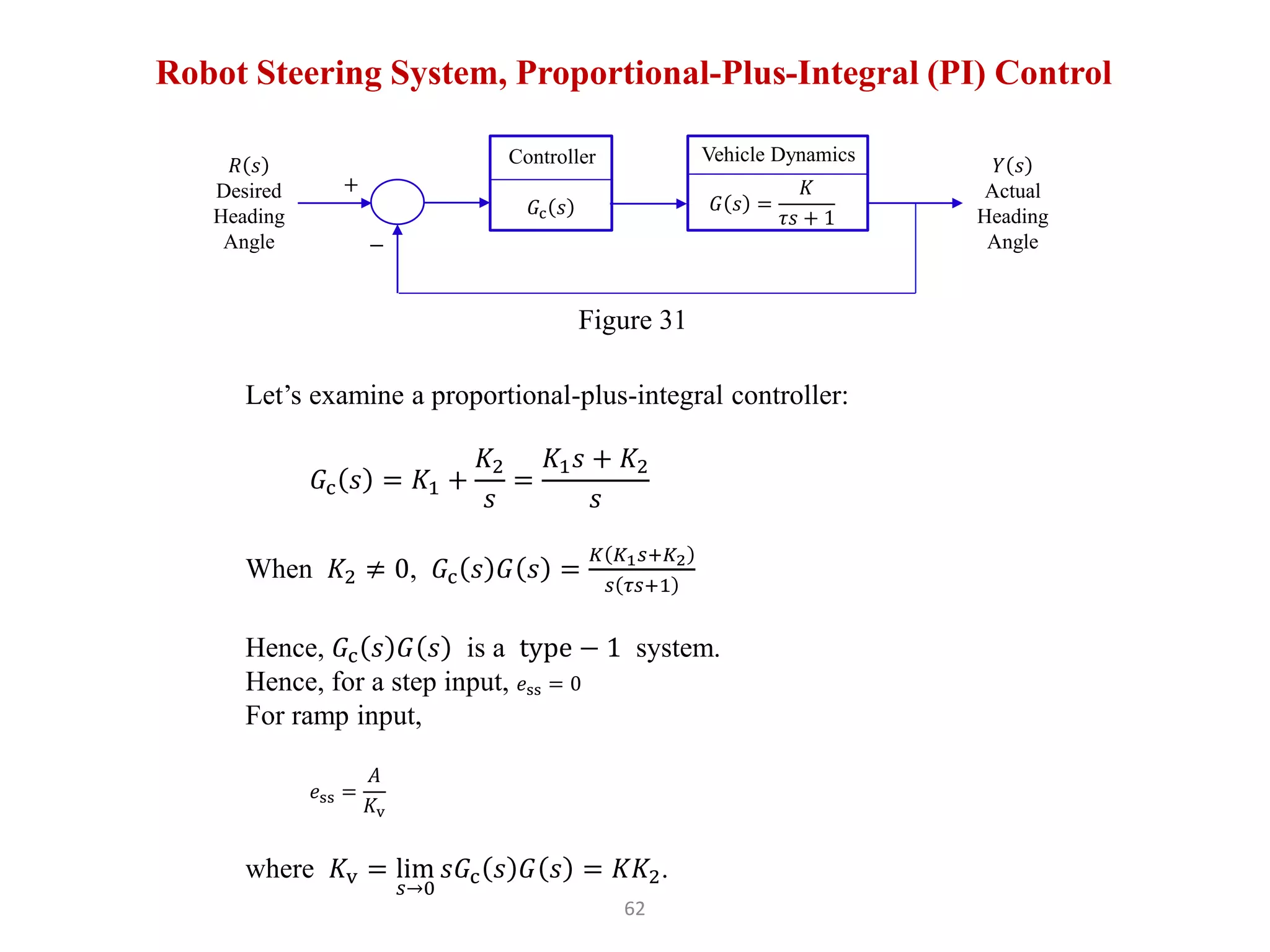
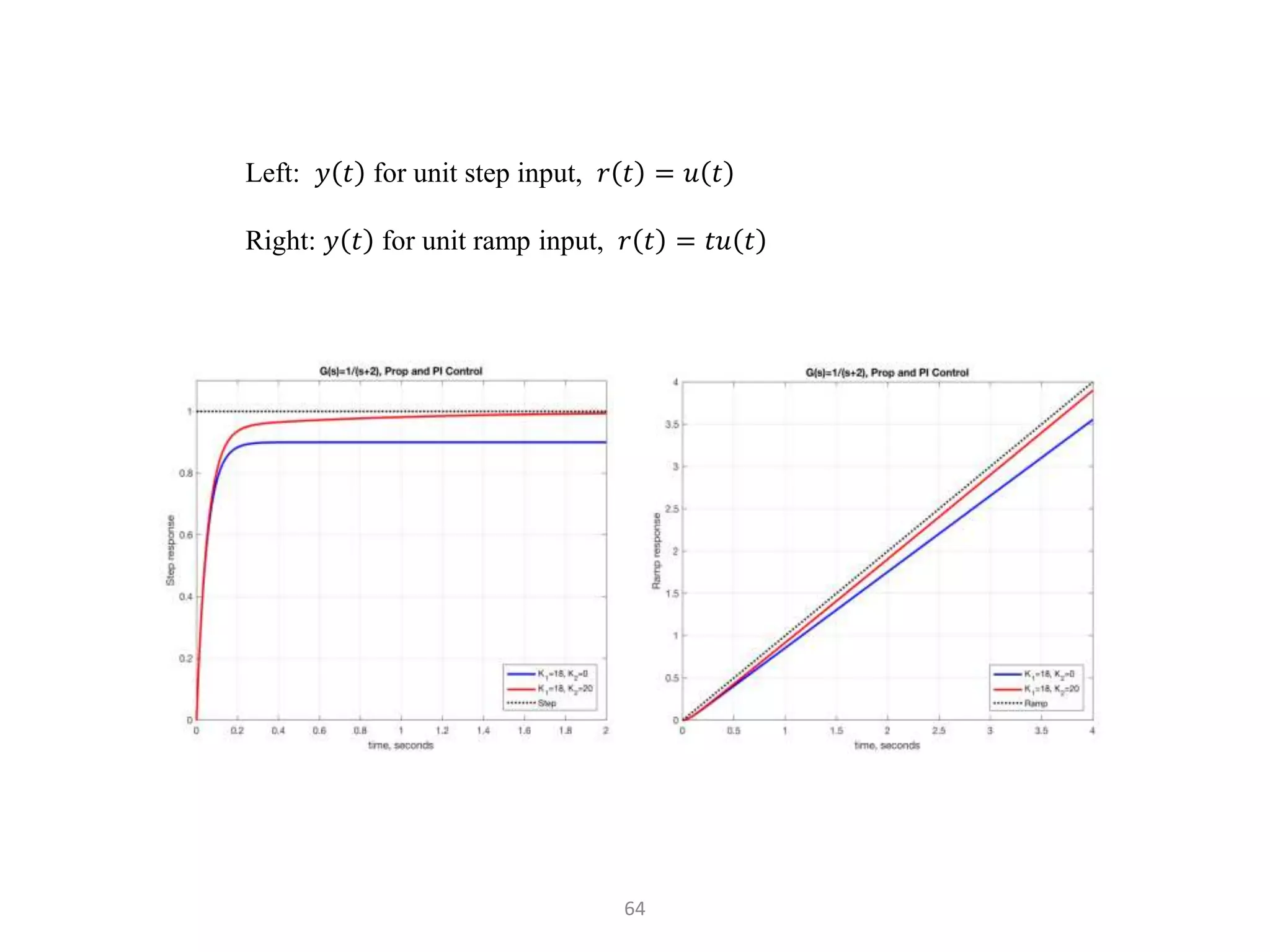
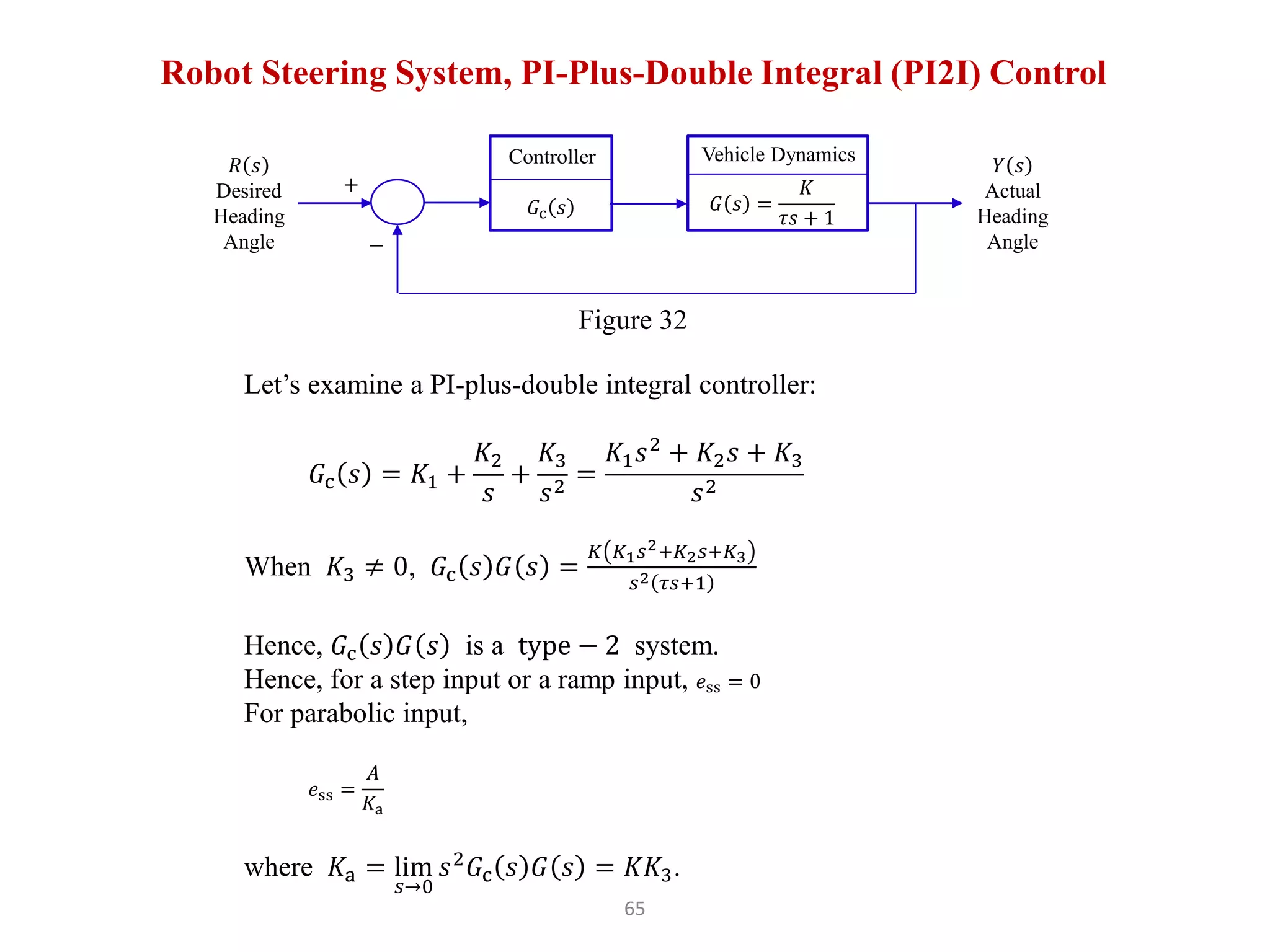
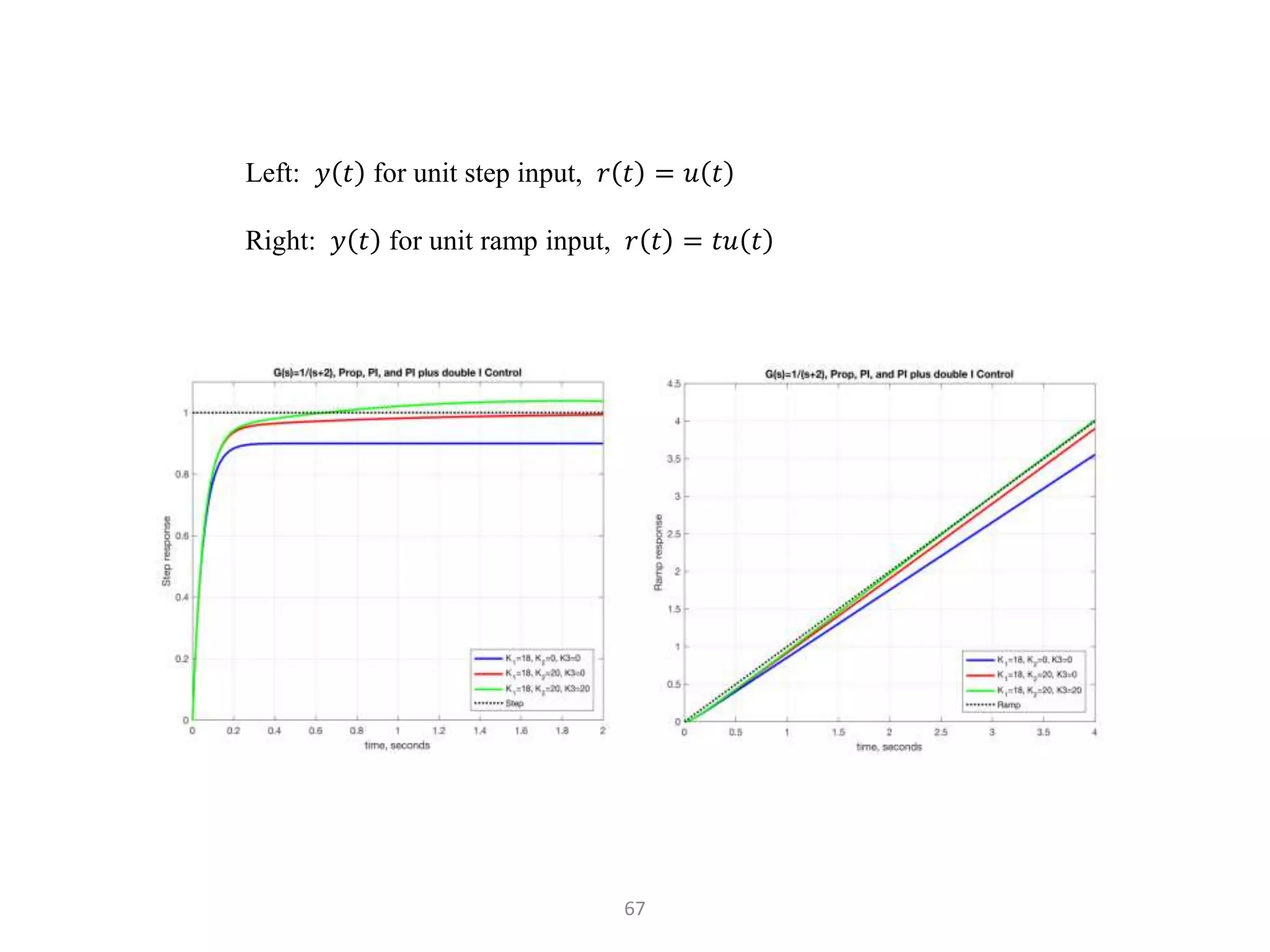
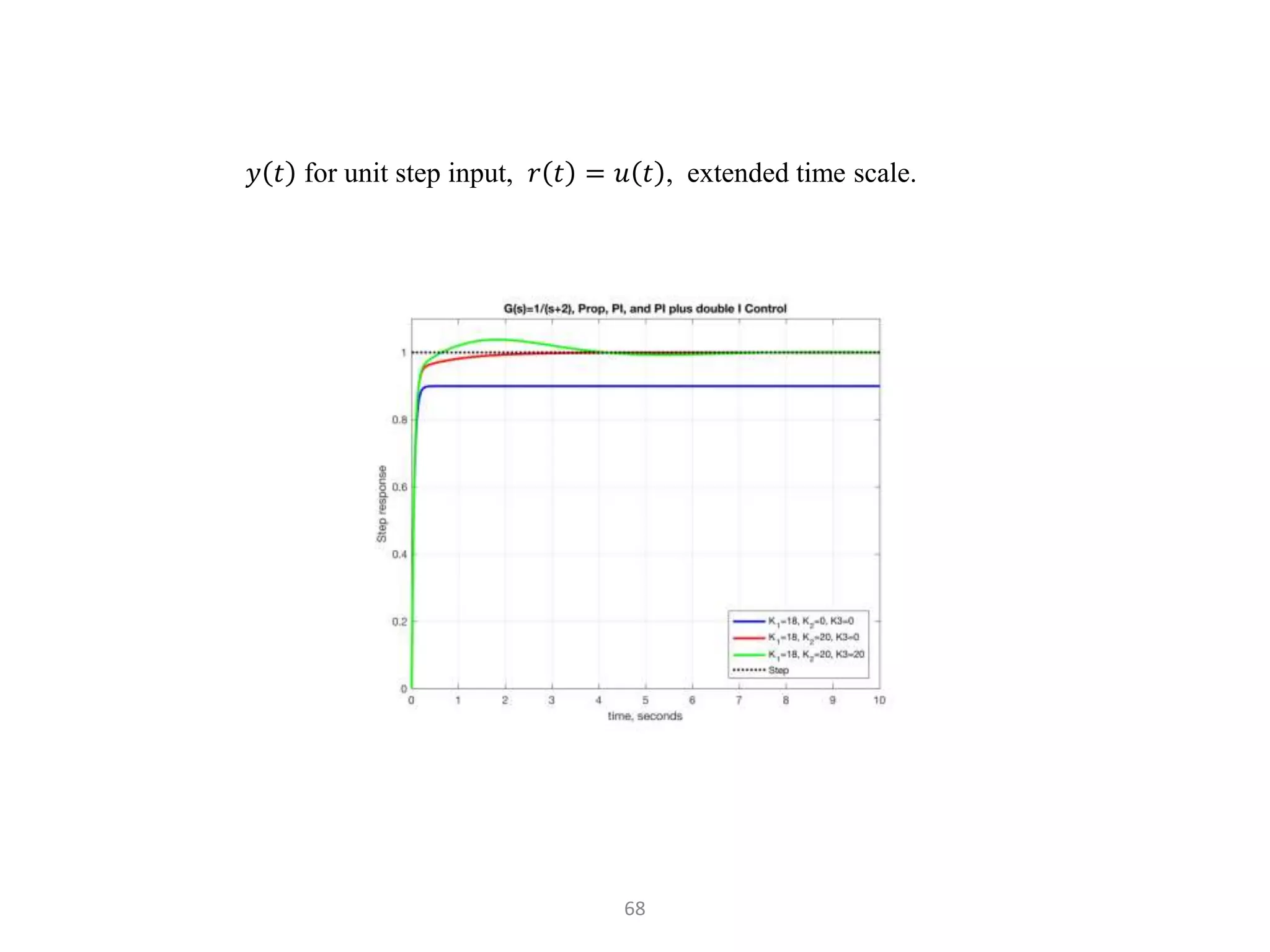
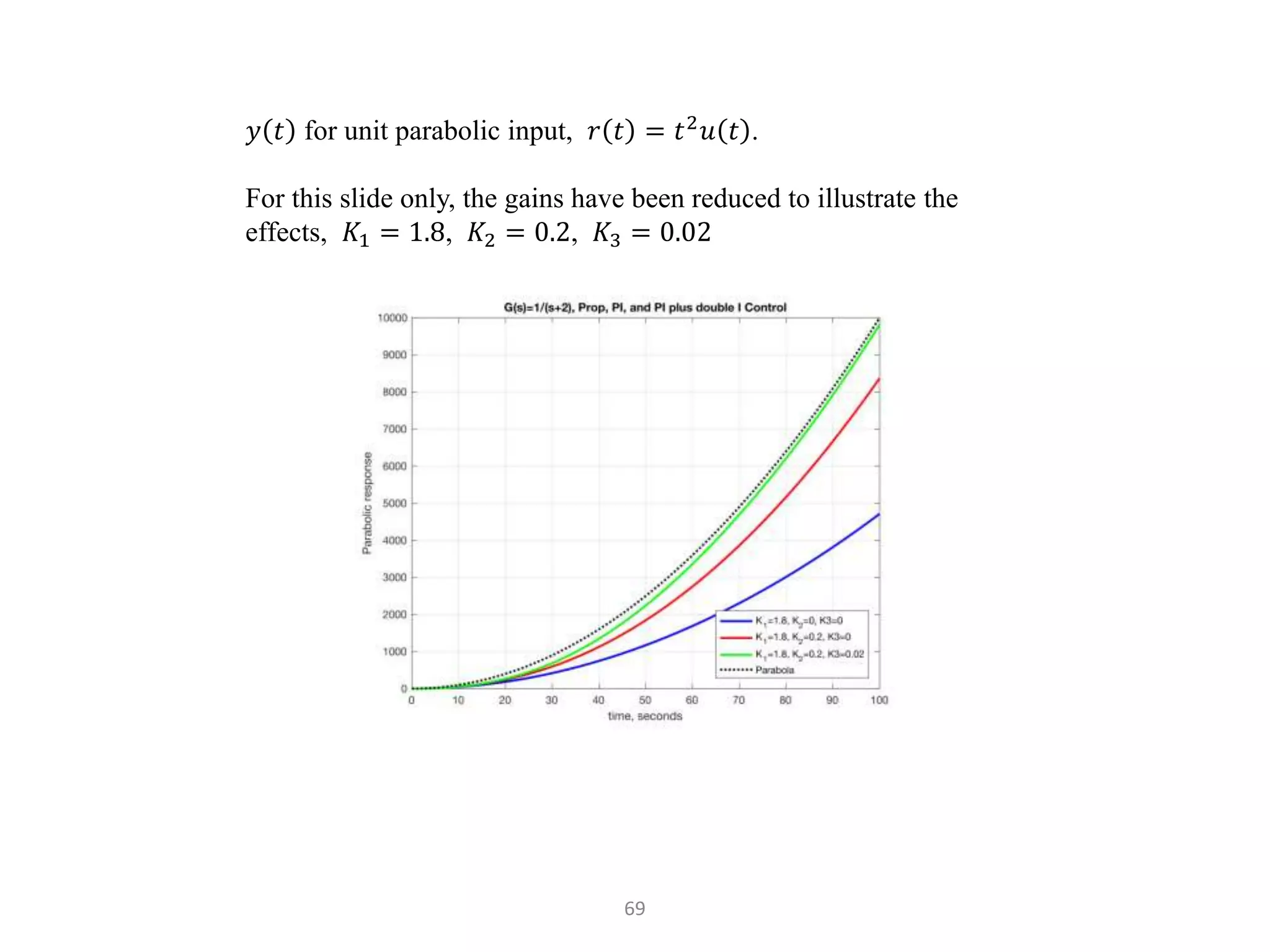
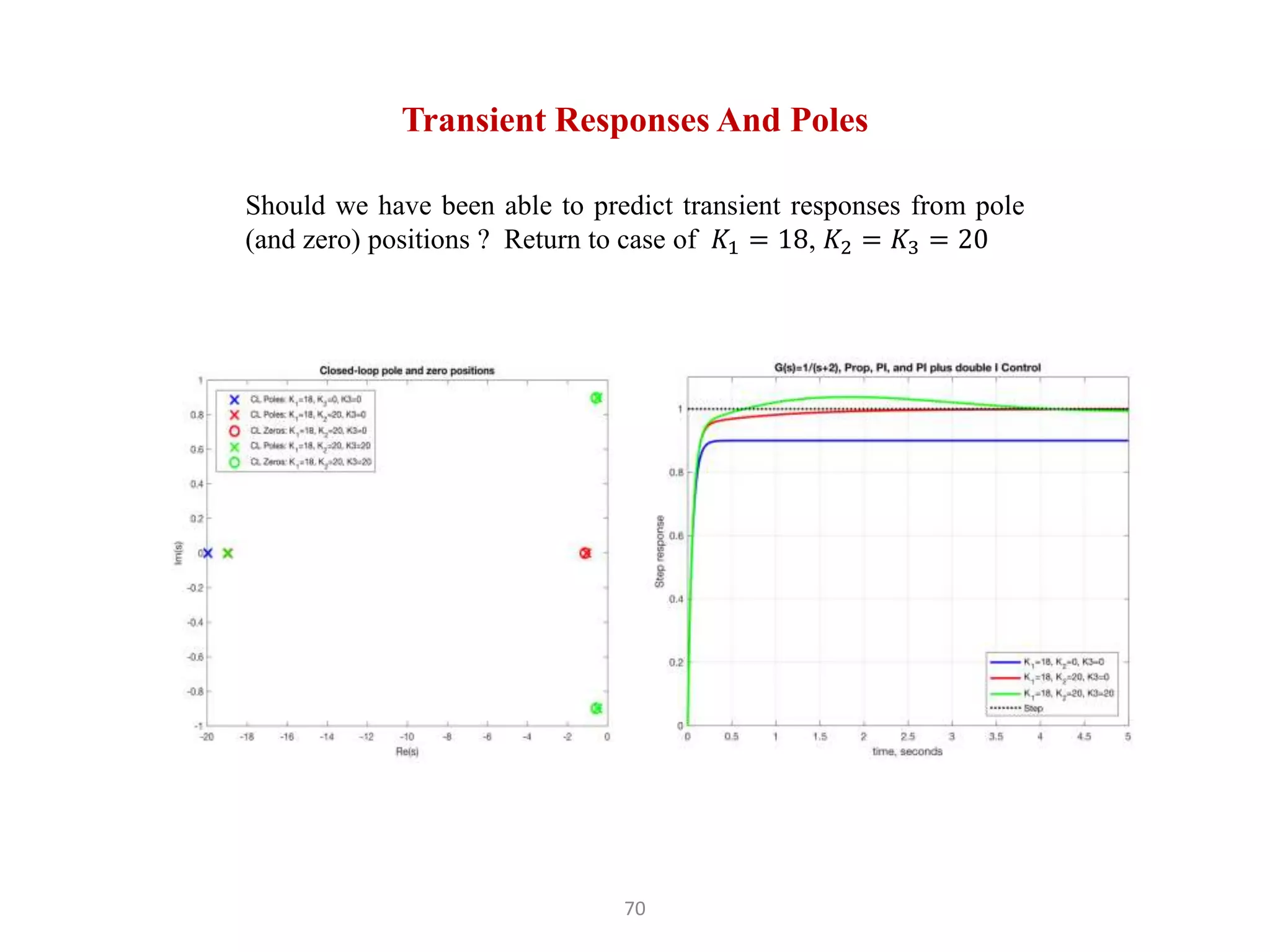
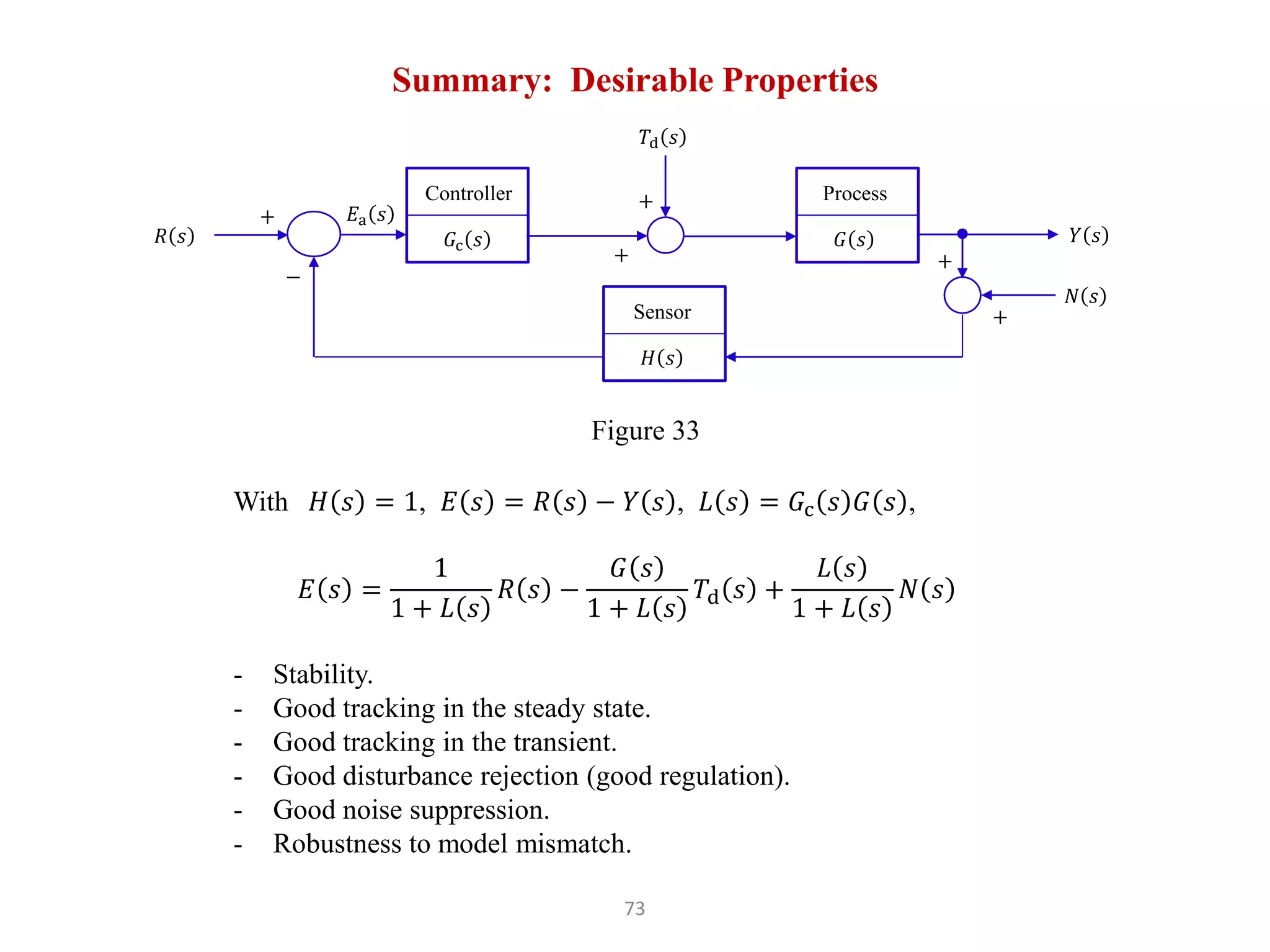
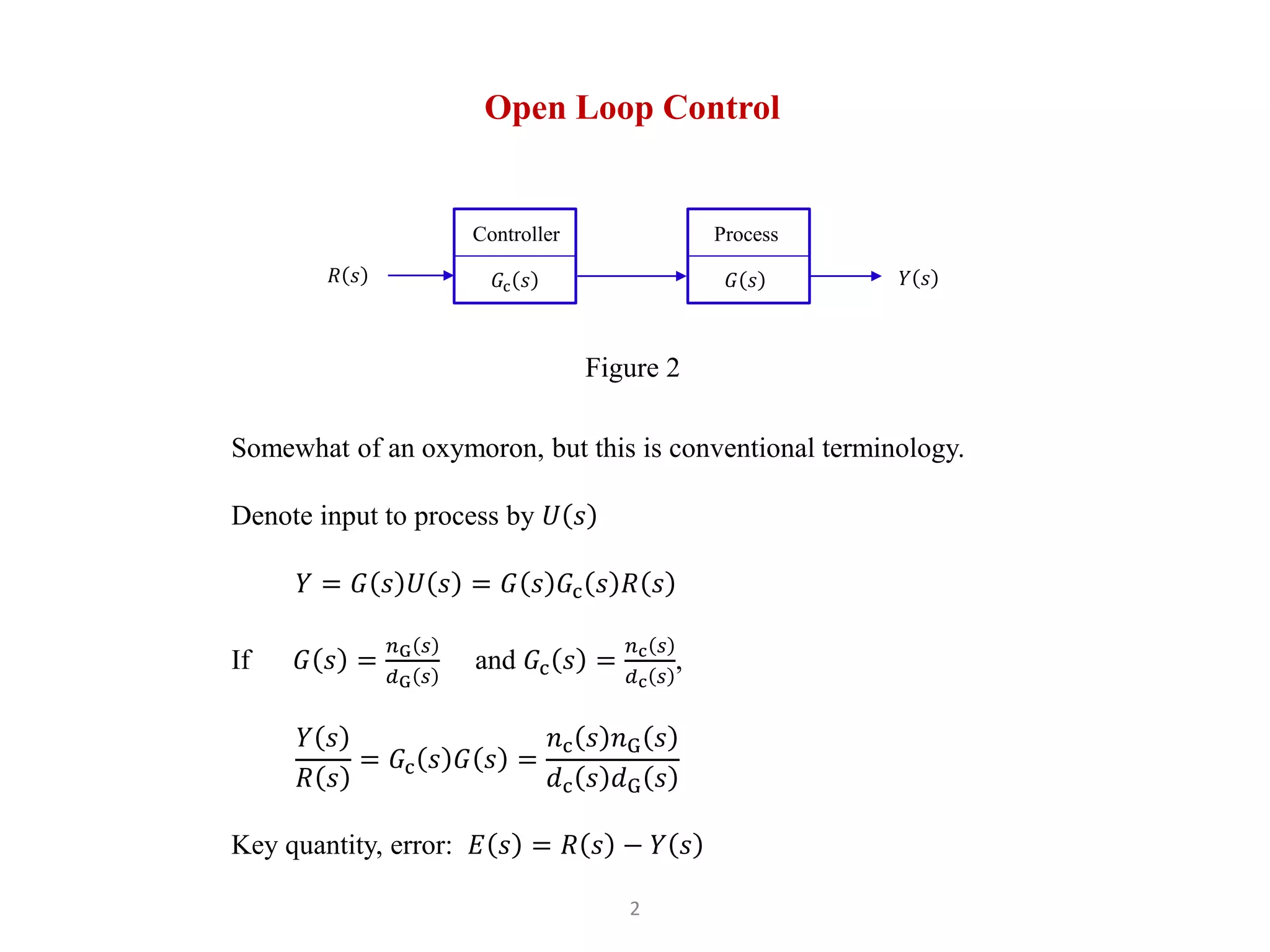
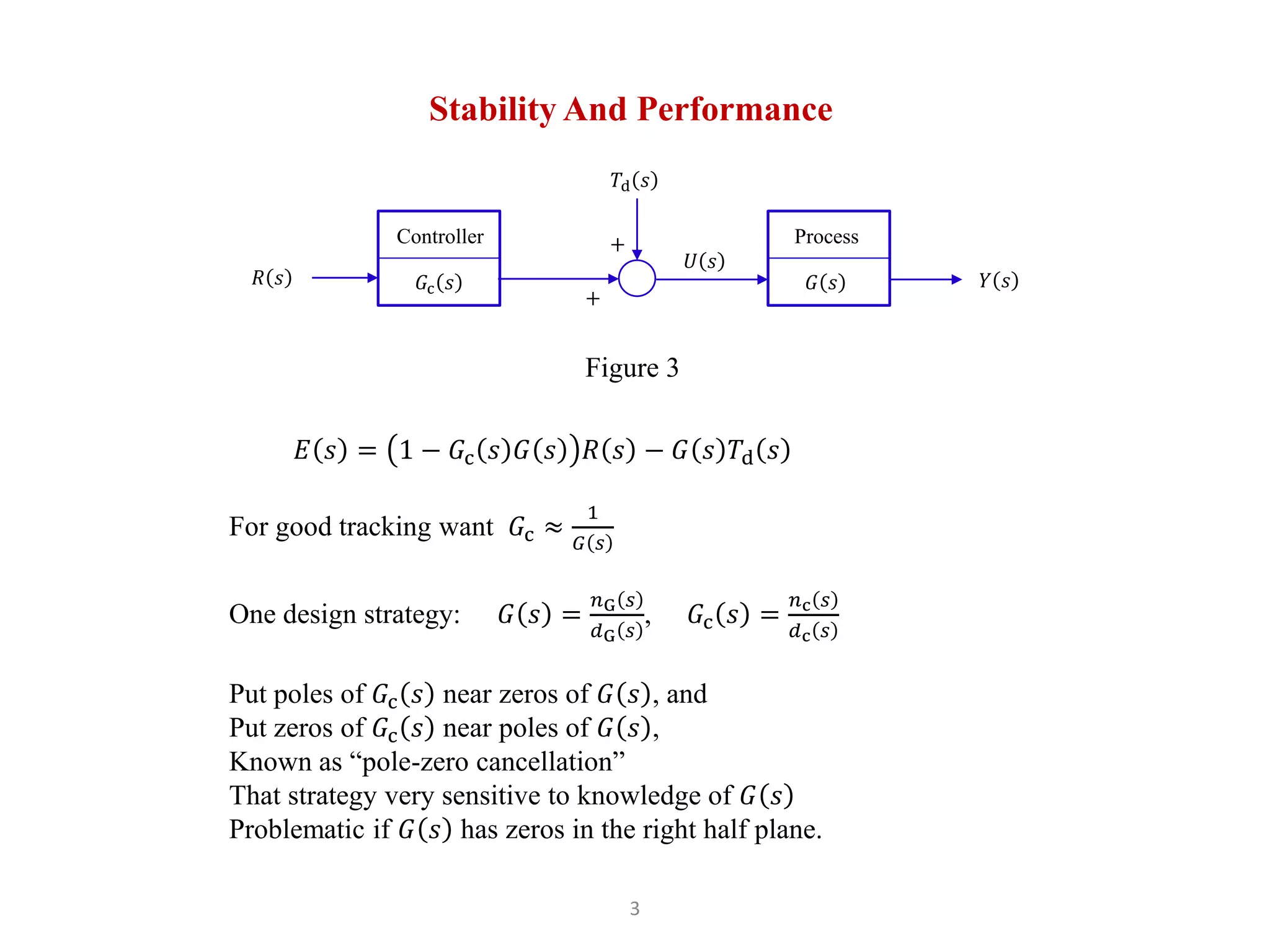
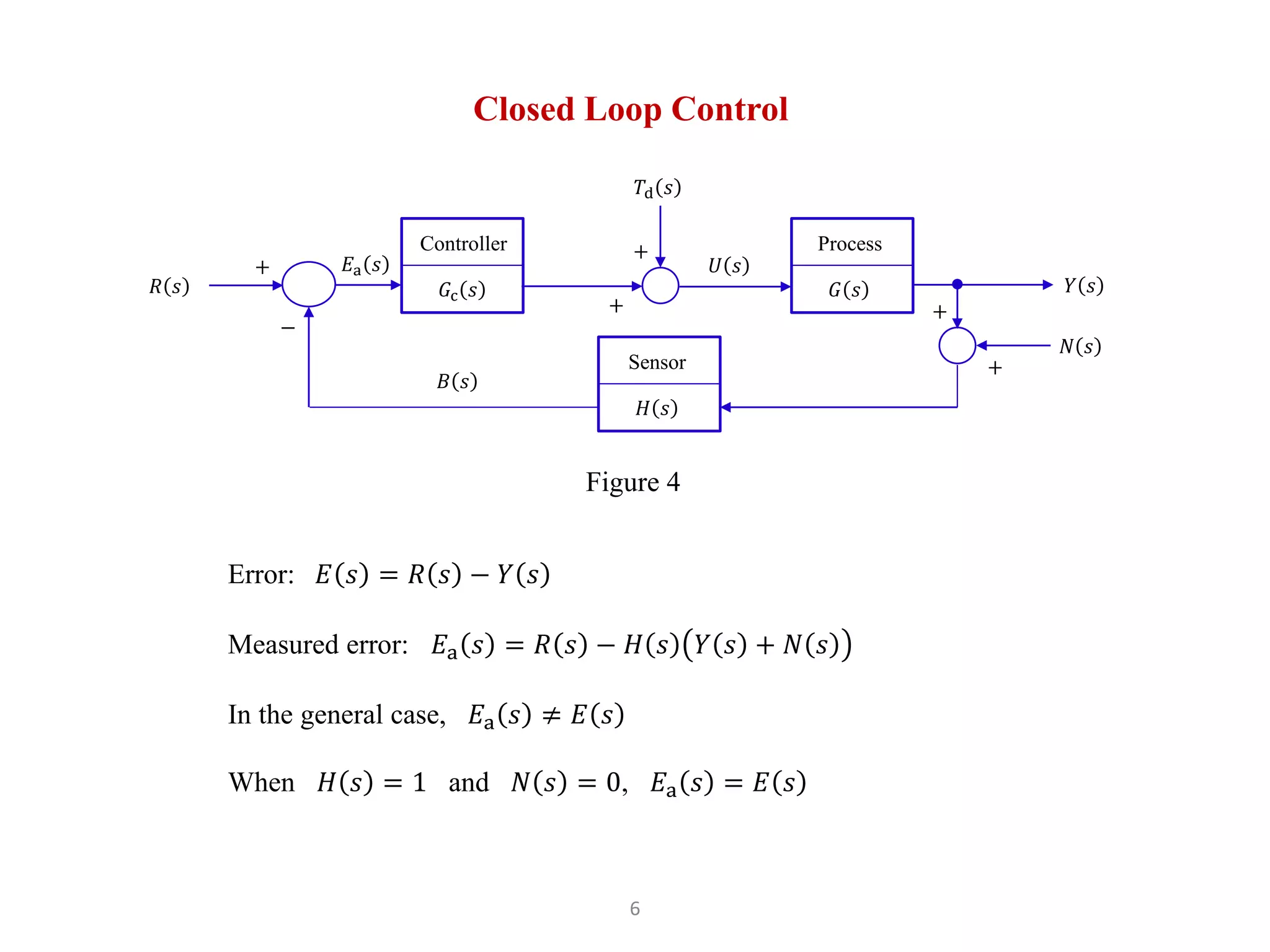
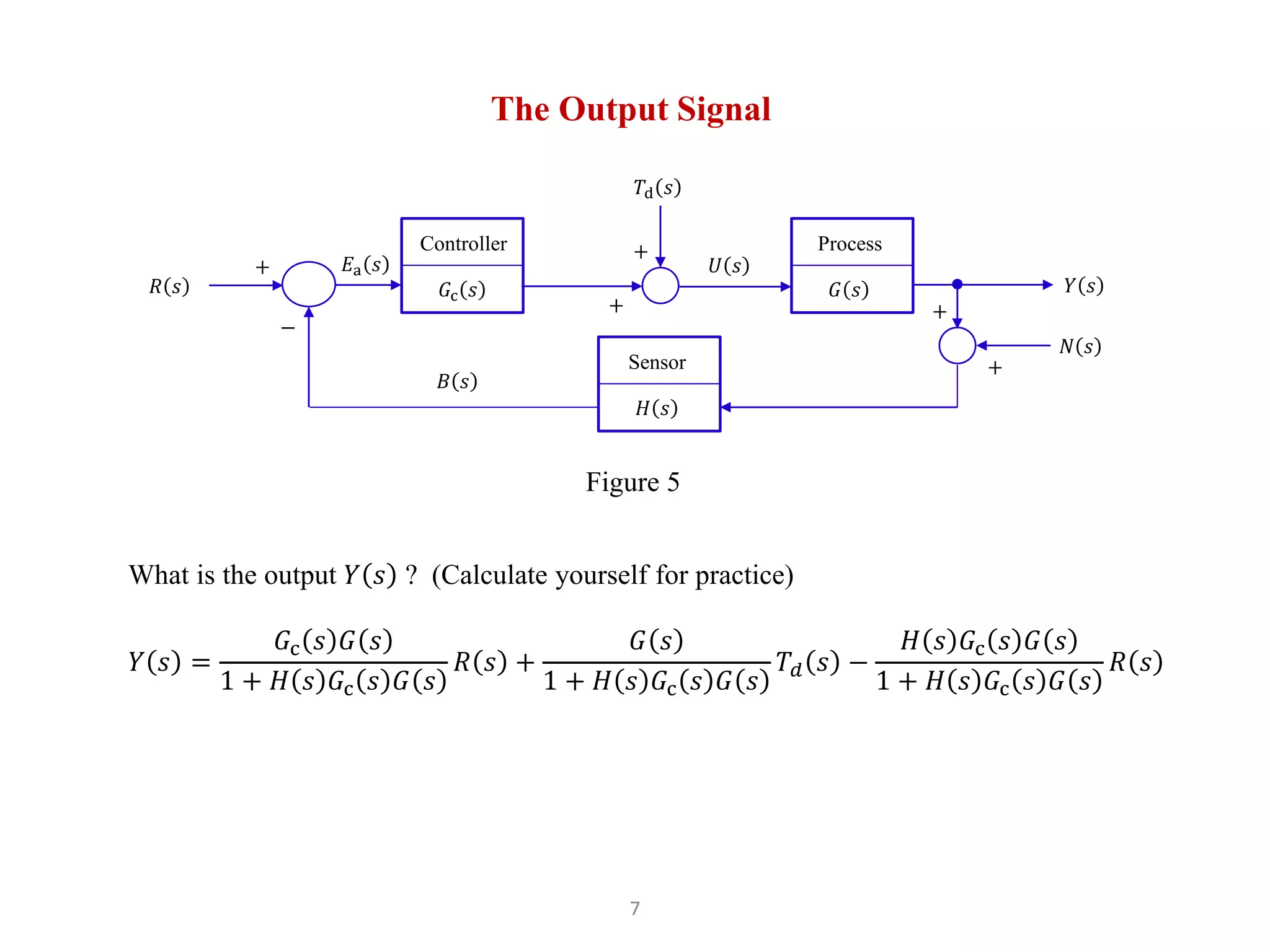
The document discusses fundamentals of feedback control systems, including: 1) Feedback control systems use a transfer function to relate the output (Y(s)) to the input (U(s)) as Y(s) = G(s)U(s), where stability requires the poles of G(s) be in the left half plane. 2) Open loop control has the error E(s) = R(s) - Y(s) where the controller Gc(s) cannot reject disturbances. 3) Closed loop control uses feedback to measure the error Ea(s) = R(s) - H(s)Y(s) + N(s) and
More Related Content
Similar to Lecture Notes: EEEC4340318 Instrumentation and Control Systems - Fundamentals of Feedback
More from AIMST University
Lecture Notes: EEEC4340318 Instrumentation and Control Systems - Fundamentals of Feedback
- 1. EEEC4340318 INSTRUMENTATION ANDCONTROL SYSTEMS Fundamentals Of Feedback FACULTY OF ENGINEERING AND COMPUTER TECHNOLOGY DIPLOMA IN ELECTRICALAND ELECTRONIC ENGINEERING Ravandran Muttiah BEng (Hons) MSc MIET
- 2. 1 Transfer Function 𝑌 𝑠= 𝐺 𝑠 𝑈 𝑠 Stability: The output 𝑦 𝑡 is bounded for all bounded inputs 𝑢 𝑡 if and only if the poles of 𝐺 𝑠 are in the open left half plane. Note that in this setting 𝑢 𝑡 is an arbitrary input, not necessarily the unit step function. Figure 1 𝑌 𝑠 𝑈 𝑠 𝐺 𝑠
- 3. 2 Open Loop Control Somewhatof an oxymoron, but this is conventional terminology. Denote input to process by 𝑈 𝑠 𝑌 = 𝐺 𝑠 𝑈 𝑠 = 𝐺 𝑠 𝐺c 𝑠 𝑅 𝑠 If 𝐺 𝑠 = 𝑛G 𝑠 𝑑G 𝑠 and 𝐺c 𝑠 = 𝑛c 𝑠 𝑑c 𝑠 , 𝑌 𝑠 𝑅 𝑠 = 𝐺c 𝑠 𝐺 𝑠 = 𝑛c 𝑠 𝑛G 𝑠 𝑑c 𝑠 𝑑G 𝑠 Key quantity, error: 𝐸 𝑠 = 𝑅 𝑠 − 𝑌 𝑠 𝐺c 𝑠 Controller 𝑌 𝑠 𝑅 𝑠 Figure 2 𝐺 𝑠 Process
- 4. 3 Stability And Performance 𝐸𝑠 = 1 − 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 − 𝐺 𝑠 𝑇d 𝑠 For good tracking want 𝐺c ≈ 1 𝐺 𝑠 One design strategy: 𝐺 𝑠 = 𝑛G 𝑠 𝑑G 𝑠 , 𝐺c 𝑠 = 𝑛c 𝑠 𝑑c 𝑠 Put poles of 𝐺c 𝑠 near zeros of 𝐺 𝑠 , and Put zeros of 𝐺c 𝑠 near poles of 𝐺 𝑠 , Known as “pole-zero cancellation” That strategy very sensitive to knowledge of 𝐺 𝑠 Problematic if 𝐺 𝑠 has zeros in the right half plane. 𝐺c 𝑠 Controller 𝑌 𝑠 𝑅 𝑠 𝑈 𝑠 Figure 3 𝐺 𝑠 Process + + 𝑇d 𝑠
- 5. 4 Controller cannot mitigateeffect of 𝑇d 𝑠 No capability for disturbance rejection. If 𝐺 𝑠 and 𝐺𝑐 𝑠 are stable, so is the “open loop”. What if 𝐺 𝑠 is not stable? In theory, controller can stabilize 𝑌 𝑠 𝑅 𝑠 by pole-zero cancellation. But difficult to implement to sufficient accuracy. Cannot stabilize 𝑌 𝑠 𝑇d 𝑠 .
- 6. 5 In practice, werarely model 𝐺 𝑠 accurately, and it may change with age, temperature and many other effects. What if 𝐺 𝑠 not perfectly known ? Let 𝑇 𝑠 = 𝑌 𝑠 𝑅 𝑠 (when 𝑇d 𝑠 = 0) Let actual process transfer function be 𝐺 𝑠 + ∆𝐺 𝑠 . What is the ratio of relative error in 𝑇 𝑠 due to relative error in 𝐺 𝑠 for small error ? That is, what is lim ∆𝐺 𝑠 →0 ∆𝑇 𝑠 𝑇 𝑠 ∆𝐺 𝑠 𝐺 𝑠 Can show (prove for yourself) that this “sensitivity” = 1 That means that for small errors the relative error in 𝑇 𝑠 is the same as the relative error in 𝐺 𝑠 . We can’t design 𝐺c 𝑠 to make it smaller.
- 7. 6 Closed Loop Control Error:𝐸 𝑠 = 𝑅 𝑠 − 𝑌 𝑠 Measured error: 𝐸a 𝑠 = 𝑅 𝑠 − 𝐻 𝑠 𝑌 𝑠 + 𝑁 𝑠 In the general case, 𝐸a 𝑠 ≠ 𝐸 𝑠 When 𝐻 𝑠 = 1 and 𝑁 𝑠 = 0, 𝐸a 𝑠 = 𝐸 𝑠 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 4 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 𝑈 𝑠
- 8. 7 The Output Signal Whatis the output 𝑌 𝑠 ? (Calculate yourself for practice) 𝑌 𝑠 = 𝐺c 𝑠 𝐺 𝑠 1 + 𝐻 𝑠 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 + 𝐺 𝑠 1 + 𝐻 𝑠 𝐺c 𝑠 𝐺 𝑠 𝑇𝑑 𝑠 − 𝐻 𝑠 𝐺c 𝑠 𝐺 𝑠 1 + 𝐻 𝑠 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 5 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 𝑈 𝑠
- 9. 8 The Error Signal,𝑯 𝒔 = 𝟏 What is the error 𝐸 𝑠 = 𝑅 𝑠 − 𝑌 𝑠 ? To simplify things, consider the case where 𝐻 𝑠 = 1 𝐸 𝑠 = 1 1 + 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐺c 𝑠 𝐺 𝑠 𝑇d 𝑠 + 𝐺c 𝑠 𝐺 𝑠 1 + 𝐺c 𝑠 𝐺 𝑠 𝑁 𝑠 Recall, 𝐸a 𝑠 = 𝐸 𝑠 only if 𝐻 𝑠 = 1 and 𝑁 𝑠 = 0 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 6 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 𝑈 𝑠
- 10. 9 Loop Gain, 𝑯𝒔 = 𝟏 Define loop gain: 𝐿 𝑠 = 𝐺c 𝑠 𝐺 𝑠 𝐸 𝑠 = 1 1 + 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐿 𝑠 𝑇d 𝑠 + 𝐿 𝑠 1 + 𝐿 𝑠 𝑁 𝑠 What do we want ? 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 7 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 𝑈 𝑠
- 11. 10 Stability, 𝑯 𝒔= 𝟏 𝐸 𝑠 = 1 1 + 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐿 𝑠 𝑇d 𝑠 + 𝐿 𝑠 1 + 𝐿 𝑠 𝑁 𝑠 Stability: Bounded inputs lead to bounded errors. For simplicity, let 𝑇𝑑 𝑠 = 0, 𝑁 = 0 𝐺 𝑠 = 𝑛G 𝑠 𝑑G 𝑠 ; 𝐺c 𝑠 = 𝑛c 𝑠 𝑑c 𝑠 ; 𝐿 𝑠 = 𝑛c 𝑠 𝑑c 𝑠 𝑛G 𝑠 𝑑G 𝑠 Hence, 1 1 + 𝐿 𝑠 = 𝑑𝑐 𝑠 𝑑𝐺 𝑠 𝑑c 𝑠 𝑑G 𝑠 + 𝑛c 𝑠 𝑛G 𝑠 ==> Closed loop poles are roots of 𝑑c 𝑠 𝑑G 𝑠 + 𝑛c 𝑠 𝑛G 𝑠 These can be in left half plane even if 𝐺 𝑠 is unstable, but they can also be in the right half plane if 𝐺 𝑠 is stable.
- 12. 11 Performance: s-domain, 𝑯𝒔 = 𝟏 𝐸 𝑠 = 1 1 + 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐿 𝑠 𝑇d 𝑠 + 𝐿 𝑠 1 + 𝐿 𝑠 𝑁 𝑠 What else do we want, in addition to stability ? Good tracking: 𝐸 𝑠 depends only weakly on 𝑅 𝑠 ⇒ 𝐿 𝑠 large where 𝑅 𝑠 large. Good disturbance rejection: ⇒ 𝐿 𝑠 large where 𝑇d 𝑠 large. Good noise suppression: ⇒ 𝐿 𝑠 small where 𝑁 𝑠 large.
- 13. 12 A Taste OfLoop Shaping, 𝑯 𝒔 = 𝟏 Possibly easier to understand in pure frequency domain, 𝑠 = j𝜔 Recall that 𝐿 𝑠 = 𝐺c 𝑠 𝐺 𝑠 , 𝐺 𝑠 : fixed; 𝐺c 𝑠 : controller to be designed. Good tracking: ⇒ 𝐿 𝑠 large where 𝑅 𝑠 large, 𝐿 j𝜔 large in the important frequency bands of 𝑟 𝑡 . Good disturbance rejection ⇒ 𝐿 𝑠 large where 𝑇d 𝑠 large, 𝐿 j𝜔 large in the important frequency bands of 𝑡d 𝑡 . Good noise suppression: ⇒ 𝐿 𝑠 small where 𝑁 𝑠 large, 𝐿 j𝜔 small in the important frequency bands of 𝑛 𝑡 . Typically, 𝐿 j𝜔 is a low-pass function. How big should 𝐿 j𝜔 be ? Any constraints ? Stability ! Any others ?
- 14. 13 Inherent Constraints, 𝑯𝒔 = 𝟏 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 8 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 Define sensitivity: 𝑆 𝑠 = 1 1+𝐿 𝑠 Define complementary sensitivity: 𝐶 𝑠 = 𝐿 𝑠 1+𝐿 𝑠 𝐸 𝑠 = 𝑆 𝑠 𝑅 𝑠 − 𝑆 𝑠 𝐺 𝑠 𝑇d 𝑠 + 𝐶 𝑠 𝑁 𝑠 Note that 𝑆 𝑠 + 𝐶 𝑠 = 1. Trading 𝑆 𝑠 against 𝐶 𝑠 , with stability, is a key part of the art of control design.
- 15. 14 Performance: Time-Domain Difficult fora arbitrary inputs. In classical control techniques, typically assessed via, (1) Nature of transient component of step response; How fast does system respond ? How long does it take to settle to new operating point. (2) Steady-state error for constant changes in position, or velocity or acceleration; that is steady-state error for: Step input; Ramp input and Parabolic input. A 𝑟 𝑡 0 r 𝑟 𝑡 0 r 𝑟 𝑡 0 r (a) Step input (b) Ramp input (c) Parabolic input Figure 9
- 16. 15 Trade-Off Example: DiskDrive System 𝐺1 𝑠 = 5000 𝑠 + 1000 Coil 𝑌 𝑠 + − 𝑅 𝑠 Figure 10 Load 𝐾a − + Disturbance 𝑇d 𝑠 𝐺2 𝑠 = 1 𝑠 𝑠 + 20 𝑌 𝑠 = 5000𝐾a 𝑠3 + 1020𝑠2 + 20000𝑠 + 5000𝐾a 𝑅 𝑠 + 𝑠 + 1000 𝑠3 + 1020𝑠2 + 20000𝑠 + 5000𝐾a 𝑇d 𝑠 Coarsely design 𝐾a to balance properties of step response and response to step disturbance.
- 17. 16 Responses For 𝑲𝐚= 𝟏𝟎 Disturbance step response and step response, Low gain: - Steady-state disturbance might not be negligible. - Slow transient response for step input.
- 18. 17 Responses For 𝑲𝐚= 𝟏𝟎, 𝟏𝟎𝟎 Disturbance step response and step response, Medium gain: - Steady-state disturbance much reduced. - Faster transient response for step input, but now some overshoot.
- 19. 18 Responses For 𝑲𝐚= 𝟏𝟎, 𝟏𝟎𝟎, 𝟏𝟎𝟎𝟎 High gain: - Steady-state disturbance almost completely rejected. - Fast transient response for step input, but now significant overshoot. - Actually can show by Routh-Hurwitz technique that loop is unstable for 𝐾a ≥ 4080. Disturbance step response and step response,
- 20. Robustness 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅𝑠 𝐸a 𝑠 Figure 11 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 What if 𝐺 𝑠 is not perfectly know ? How does 𝑇 𝑠 = 𝑌 𝑠 𝑅 𝑠 change as 𝐺 𝑠 changes ? As in open loop case, look at ratio of relative error in 𝑇 𝑠 due to a relative error in 𝐺 𝑠 , for small errors, lim ∆𝐺 𝑠 →0 ∆𝑇 𝑠 𝑇 𝑠 ∆𝐺 𝑠 𝐺 𝑠 For an open loop system this sensitivity is 1. For the closed loop system, with 𝐻 𝑠 = 1, this sensitivity is 𝑆 𝑠 = 1 1+𝐺c 𝑠 𝐺 𝑠 Now can design controller to manage sensitivity. 19
- 21. Open Loop vsClosed Loop 𝐺c 𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 12 𝐺 𝑠 Process 𝐻 𝑠 Sensor 𝐵 𝑠 + + 𝑇d 𝑠 + + 𝑁 𝑠 20 𝐺c 𝑠 Controller 𝑌 𝑠 𝑅 𝑠 𝑈 𝑠 Figure 13 𝐺 𝑠 Process + + 𝑇d 𝑠
- 22. 21 Error: 𝐸 𝑠= 𝑅 𝑠 − 𝑌 𝑠 ; Loop gain: 𝐿 𝑠 = 𝐺𝑐 𝑠 𝐺 𝑠 , Open loop, with process input 𝐺𝑐 𝑠 𝑅 𝑠 + 𝑇d 𝑠 𝐸OL 𝑠 = 1 − 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 𝑇d 𝑠 Closed loop, with 𝐻 𝑠 = 1, 𝐸CL 𝑠 = 1 1 + 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐿 𝑠 𝑇d 𝑠 + 𝐿 𝑠 1 + 𝐿 𝑠 𝑁 𝑠
- 23. 22 Advantages Of Feedback (1)Can mitigate disturbances. (2) Can stabilise (most) unstable processes. (3) Can mitigate errors in the model of process.
- 24. 23 Price Of Feedback (1)More components than open loop. (2) Introduces noise, but can “shape” the response. (3) Less gain: 𝐺c 𝑠 𝐺 𝑠 1+𝐺c 𝑠 𝐺 𝑠 instead of 𝐺c 𝑠 𝐺 𝑠 . (4) Potential for instability even when 𝐺 𝑠 is stable. More complicated to analyse and design, but often advantages are worth the price.
- 25. 24 A Second-Order System Nowexamine, in detail, a particular class of second order systems. 𝐺 𝑠 = 𝜔𝑛 2 𝑠 𝑠 + 2𝜁𝜔𝑛 2nd Order System 𝑌 𝑠 + − 𝑅 𝑠 Figure 14 𝑌 𝑠 = 𝐺 𝑠 1 + 𝐺 𝑠 𝑅 𝑠 = 𝜔𝑛 2 𝑠2 + 2𝜁𝜔𝑛𝑠 + 𝜔𝑛 2 𝑅 𝑠
- 26. 25 Step Response What isthe step response ? Set 𝑅 𝑠 = 1 𝑠 ; take inverse Laplace transform of 𝑌 𝑠 𝑌 𝑠 = 𝜔𝑛 2 𝑠 𝑠2 + 2𝜁𝜔𝑛𝑠 + 𝜔𝑛 2 For the case of 0 < 𝜁 < 1, 𝑦 𝑡 = 1 − 1 𝛽 𝑒−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 where, 𝛽 = 1 − 𝜁2 and 𝜃 = cos−1 𝜁. Recall pole positions of 𝐺 𝑠 1+𝐺 𝑠 (ignore the zero):
- 27. 26 × × j𝜔𝑛 1 −𝜁2 −j𝜔𝑛 1 − 𝜁2 j𝜔 𝑠1 𝑠2 −𝜁𝜔𝑛 𝜔𝑛 𝜃 = cos−1 𝜁 −2𝜁𝜔𝑛 𝜎 Figure 15 0
- 28. 27 Figure 16 Typical StepResponses, Fixed 𝝎𝒏
- 29. 28 Figure 17 Typical StepResponses, Fixed 𝜁
- 30. 29 Key Parameters Of(Under-Damped) Step Response with 𝛽 = 1 − 𝜁2 and 𝜃 = cos−1 𝜁, 𝑦 𝑡 = 1 − 1 𝛽 𝑒−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 Figure 18
- 31. 30 Peak Time AndPeak Value 𝑦 𝑡 = 1 − 1 𝛽 e−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 Peak time: first time d𝑦 𝑡 d𝑡 = 0 Can show that this corresponds to 𝜔𝑛𝛽𝑇p = π Hence, 𝑇p = π 𝜔𝑛 1−𝜁2 Hence, peak value, 𝑀pt = 1 + e − 𝜁π 1−𝜁2
- 32. 31 Percentage Overshoot Let 𝑓𝑣denote the final value of the step response. Percentage overshoot defined as: Percentage Overshoot = 100 𝑀pt−𝑓𝑣 𝑓𝑣 In our example, 𝑓𝑣 = 1, and hence Percentage Overshoot = 100e − ζπ 1−ζ2
- 33. 32 Overshoot vs PeakTime This is one of the classic trade-offs in control. Figure 19
- 34. 33 Steady-State Error, 𝒆𝐬𝐬 Ingeneral this is not zero. (See “Steady-Sate Error” section) However, for our second-order system, 𝑦 𝑡 = 1 − 1 𝛽 e−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 Hence, ess = 0 Figure 20
- 35. 34 𝑦 𝑡 =1 − 1 𝛽 e−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 How long does it take to get (and stay) within ±𝑥 % of final value ? Tricky. Instead, approximate by time constants of envelopes: 1 ± 1 𝛽 e−𝜁𝜔𝑛𝑡 Settling Time
- 36. 35 5 % SettlingTime Figure 21
- 37. 36 After 3 timeconstants envelope error reduced by factor 1 e3 becomes ≈ 5 % of envelope error at 𝑡 = 0 In figure, 𝜁 = 0.5, 𝜔𝑛 = 1, error bounds at ±0.05: Time constant, 1 𝜁𝜔𝑛 = 2. After 𝑡 = 6, envelopes are almost within ±5 %. Response is within ±5 %. Hence, 𝑇s,5 ≈ 3 𝜁𝜔𝑛 ; approximately good for 𝜁 ≤ 0.9
- 38. 37 Figure 22 2 %Settling Time
- 39. 38 After 4 timeconstants envelope error reduced by factor 1 e4 becomes ≈ 2 % of envelope error at 𝑡 = 0 In figure, 𝜁 = 0.5, 𝜔𝑛 = 1, error bounds at ±0.02: After 𝑡 = 8, envelopes are almost within ±2 %. Response is almost within ±2 %. Hence, 𝑇s,2 ≈ 4 𝜁𝜔𝑛 ; approximately good for 𝜁 ≤ 0.9
- 40. 39 Rise Time (Under-Damped) 𝑦𝑡 = 1 − 1 𝛽 e−𝜁𝜔𝑛𝑡 sin 𝜔𝑛𝛽𝑡 + 𝜃 How long to get to the target (for first time) ? 𝑇𝑟, the smallest 𝑡 such that 𝑦 𝑡 = 1 Figure 23
- 41. 40 What is 𝑇rin over-damped case ? ∞ Hence, typically use 𝑇r1, the 10 % − 90 % rise time. 𝟏𝟎 % − 𝟗𝟎 % Rise Time
- 42. 41 Difficult to getan accurate formula. Linear approximation for 0.3 ≤ 𝜁 ≤ 0.8 (under-damped). Figure 24
- 43. 42 Design Problem 𝐾 𝑠 𝑠+ 𝑝 𝑌 𝑠 + − 𝑅 𝑠 Figure 25 For what values of 𝐾 and 𝑝 is, (1) The settling time ≤ 4 secs, and (2) The percentage overshoot ≤ 4.3 % ? 𝑇 𝑠 = 𝐺 𝑠 1 + 𝐺 𝑠 = 𝐾 𝑠2 + 𝑝𝑠 + 𝐾 = 𝜔𝑛 2 𝑠2 + 2𝜁𝜔𝑛𝑠 + 𝜔𝑛 2 where 𝜔𝑛 = 𝐾 and 𝜁 = 𝑝 2 𝐾
- 44. 43 Pole Positions 𝑇𝑠 ≈ 4 𝜁𝜔𝑛 PercentageOvershoot = 100e − 𝜁𝜋 1−𝜁2 For 𝑇𝑠 ≤ 4, 𝜁𝜔𝑛 ≥ 1 For percentage overshoot ≤ 4.3 %, 𝜁 ≥ 1 2 Where should we put the poles of 𝑇 𝑠 ?
- 45. 44 Figure 26 𝜁𝜔𝑛 ≥1 𝜁 ≥ 1 2 𝑠1, 𝑠2 = −𝜁𝜔𝑛 ± j𝜔𝑛 1 − 𝜁2 = −𝜔𝑛 cos 𝜃 ± j𝜔𝑛 sin 𝜃 where 𝜃 = cos−1 𝜁 .
- 46. 45 Final Design Constraints 𝜁𝜔𝑛≥ 1 𝜁 ≥ 1 2 𝑝 ≥ 2 𝑝 ≥ 2𝐾 Figure 27
- 47. 46 Caveat Our work ontransient response has been for systems with, 𝑇 𝑠 = 𝜔𝑛 2 𝑠2 + 2𝜁𝜔𝑛𝑠 + 𝜔𝑛 2 What about other systems ?
- 48. 47 Poles, Zeros AndTransient Response Consider a general transfer function, 𝑇 𝑠 = 𝑌 𝑠 𝑅 𝑠 Step response: 𝑌 𝑠 = 𝑇 𝑠 1 𝑠 Consider case with DC gain = 1; no repeated poles. Partial fraction expansion, 𝑌 𝑠 = 1 𝑠 + 𝑖 𝐴𝑖 𝑠 + 𝜎𝑖 + 𝑘 𝐵𝑘𝑠 + 𝐶𝑘 𝑠2 + 2𝛼𝑘𝑠 + 𝛼𝑘 2 + 𝜔𝑘 2 Step response, 𝑦 𝑡 = 1 + 𝑖 𝐴𝑖e−𝛼𝑖𝑡 + 𝑘 𝐷𝑘e−𝛼𝑘𝑡 sin 𝜔𝑘𝑡 + 𝜃𝑘
- 49.
- 50. 49 Steady-State Error 𝐺c 𝑠 Controller 𝑌𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 29 𝐺 𝑠 Process 𝐸 𝑠 = 𝑅 𝑠 − 𝑌 𝑠 = 1 1 + 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 If the conditions are satisfied, the final value theorem gives steady- state tracking error: ess = lim 𝑡→∞ 𝑒 𝑡 = lim 𝑠→0 s 1 1 + 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 One of the fundamental reasons for using feedback, despite the cost of the extra components, is to reduce this error. We will examine this error for the step, ramp and parabolic inputs.
- 51. 50 A 𝑟 𝑡 0 r 𝑟𝑡 0 r 𝑟 𝑡 0 r (a) Step input (b) Ramp input (c) Parabolic input Figure 29
- 52. 51 Step Input 𝑒ss =lim 𝑡→∞ 𝑒 𝑡 = lim 𝑠→0 𝑠 1 1 + 𝐺c 𝑠 𝐺 𝑠 𝑅 𝑠 Step input: 𝑅 𝑠 = 𝐴 𝑠 𝑒ss = lim 𝑠→0 𝑠 𝐴 𝑠 1 + 𝐺c 𝑠 𝐺 𝑠 = 𝐴 1 + lim 𝑠→0 𝐺c 𝑠 𝐺 𝑠 Now let’s examine 𝐺c 𝑠 𝐺 𝑠 . Factorize numerator and denominator. 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝑖=1 𝑀 𝑠 + 𝑧𝑖 𝑠𝑁 𝑖=1 𝑄 𝑠 + 𝑝𝑘 where 𝑧𝑖 ≠ 0 and 𝑝𝑘 ≠ 0. Limit as 𝑠 → 0 depends strongly on 𝑁. If 𝑁 > 0, lim 𝑠→0 𝐺c 𝑠 𝐺 𝑠 → ∞ and 𝑒ss = 0 If 𝑁 = 0, 𝑒ss = 𝐴 1 + 𝐺c 0 𝐺 0
- 53. 52 System Types Since 𝑁plays such a key role, it has been given a name. It is called the type number. Hence, for systems of type 𝑁 ≥ 1, 𝑒ss for a step input is zero. For systems of type 0, 𝑒ss = 𝐴 1+𝐺c 0 𝐺 0
- 54. 53 Position Error Constant Fortype − 0 systems, 𝑒ss = 𝐴 1+𝐺c 0 𝐺 0 Sometimes written as, 𝑒ss = 𝐴 1+𝐾position where 𝐾position is the position error constant. Recall 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝑖=1 𝑀 𝑠+𝑧𝑖 𝑠𝑁 𝑖=1 𝑄 𝑠+𝑝𝑘 Therefore, for a type-0 system, 𝐾position = lim 𝑠→0 Gc s 𝐺 𝑠 = 𝐾 𝑖=1 𝑀 𝑧𝑖 𝑠𝑁 𝑖=1 𝑄 𝑝𝑘 Note that this can be computed from positions of the non-zero poles and zeros.
- 55. 54 Ramp Input The rampinput, which represents a step change in velocity is 𝑟 𝑡 = 𝐴𝑡. Therefore 𝑅 𝑠 = 𝐴 𝑠2 Assuming conditions of final value theorem are satisfied, 𝑒ss = lim 𝑠→0 𝑠 𝐴 𝑠2 1 + 𝐺c 𝑠 𝐺 𝑠 = lim 𝑠→0 𝐴 𝑠 + 𝑠𝐺c 𝑠 𝐺 𝑠 = lim 𝑠→0 𝐴 𝑠𝐺c 𝑠 𝐺 𝑠 Again, type number will play a key role.
- 56. 55 Velocity Error Constant Fora ramp input, 𝑒ss = lim 𝑠→0 𝐴 𝑠𝐺c 𝑠 𝐺 𝑠 Recall 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝑖=1 𝑀 𝑠+𝑧𝑖 𝑠𝑁 𝑖=1 𝑄 𝑠+𝑝𝑘 For type − 0 systems, 𝐺c 𝑠 𝐺 𝑠 has no poles at origin. Hence, 𝑒ss → ∞ For type − 1 systems, 𝐺c 𝑠 𝐺 𝑠 has one pole at the origin. Hence, 𝑒ss = 𝐴 𝐾v , where 𝐾v = 𝐾 𝑖 𝑧𝑖 𝑘 𝑝𝑘 Note 𝐾v can be computed from non-zero poles and zeros. Suggests formal definition of velocity error constant, 𝐾v = lim 𝑠→0 𝑠𝐺c 𝑠 𝐺 𝑠 For type − 𝑁 systems with 𝑁 ≥ 2, for a ramp input 𝑒ss = 0.
- 57. 56 Parabolic Input The parabolicinput, which represents a step change in acceleration is 𝑟 𝑡 = 𝐴𝑡2 2 . Therefore 𝑅 𝑠 = 𝐴 𝑠3 Assuming conditions of final value theorem are satisfied, 𝑒ss = lim 𝑠→0 𝑠 𝐴 𝑠3 1 + 𝐺c 𝑠 𝐺 𝑠 = lim 𝑠→0 𝐴 𝑠2𝐺c 𝑠 𝐺 𝑠 Again, type number will play a key role.
- 58. 57 Acceleration Error Constant Fora parabolic input, 𝑒ss = lim 𝑠→0 𝐴 𝑠2𝐺c 𝑠 𝐺 𝑠 Recall 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝑖=1 𝑀 𝑠+𝑧𝑖 𝑠𝑁 𝑖=1 𝑄 𝑠+𝑝𝑘 For type − 0 and type − 1 systems, 𝐺c 𝑠 𝐺 𝑠 has no poles at origin. Hence, 𝑒ss → ∞ For type − 2 systems, 𝐺c 𝑠 𝐺 𝑠 has two poles at the origin. Hence, 𝑒ss = 𝐴 𝐾a , where 𝐾a = 𝐾 𝑖 𝑧𝑖 𝑘 𝑝𝑘 Again, 𝐾a can be computed from non-zero poles and zeros. Suggests formal definition of acceleration error constant, 𝐾a = lim 𝑠→0 𝑠2 𝐺c 𝑠 𝐺 𝑠 For type − 𝑁 systems with 𝑁 ≥ 3, for a parabolic input 𝑒ss = 0.
- 59. 58 Summary Of Steady-StateErrors Number of Integrations in 𝐺c 𝑠 𝐺 𝑠 , Type Number Input Step, 𝑟 𝑡 = 𝐴, 𝑅 𝑠 = 𝐴 𝑠 Ramp, 𝐴𝑡, 𝐴 𝑠2 Parabola, 𝐴𝑡2 2, 𝐴 𝑠3 0 𝑒ss = 𝐴 1 + 𝐾position Infinite Infinite 1 𝑒ss = 0 𝐴 𝐾v Infinite 2 𝑒ss = 0 0 𝐴 𝐾a Table 1: Summary of Steady-State Errors
- 60. 59 Robot Steering System,Proportional (P) Control 𝐺c 𝑠 Controller 𝑌 𝑠 Actual Heading Angle + − 𝑅 𝑠 Desired Heading Angle Figure 30 𝐺 𝑠 = 𝐾 𝜏𝑠 + 1 Vehicle Dynamics Let’s examine a proportional controller: 𝐺c 𝑠 = 𝐾1 𝐺c 𝑠 𝐺 𝑠 = 𝐾1𝐾 𝜏𝑠 + 1 Hence, 𝐺c 𝑠 𝐺 𝑠 is a type − 0 system. Hence, for a step input, 𝑒ss = 𝐴 1 + 𝐾position where 𝐾position = 𝐾1𝐾.
- 61. 60 Robot Steering System,P Control Example Let’s 𝐺 𝑠 = 1 𝑠+2 = 0.5 0.5𝑠+1 Proportional control, 𝐺c 𝑠 = 𝐾1. Choose 𝐾1 = 18. Since 𝐺c 𝑠 𝐺 𝑠 is type − 0: - Finite steady-state error for a step, - Unbounded steady-state error for a ramp. In this example, 𝐾position = 𝐾𝐾1 = 9 The steady-state error for a step input will be 1 1+𝐾p = 10 % of the height of the step. For a unit step the steady-state error will be 0.1
- 62. 61 Left: 𝑦 𝑡for unit step input, 𝑟 𝑡 = 𝑢 𝑡 Right: 𝑦 𝑡 for unit ramp input, 𝑟 𝑡 = 𝑡𝑢 𝑡
- 63. 62 Robot Steering System,Proportional-Plus-Integral (PI) Control 𝐺c 𝑠 Controller 𝑌 𝑠 Actual Heading Angle + − 𝑅 𝑠 Desired Heading Angle Figure 31 𝐺 𝑠 = 𝐾 𝜏𝑠 + 1 Vehicle Dynamics Let’s examine a proportional-plus-integral controller: 𝐺c 𝑠 = 𝐾1 + 𝐾2 𝑠 = 𝐾1𝑠 + 𝐾2 𝑠 When 𝐾2 ≠ 0, 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝐾1𝑠+𝐾2 𝑠 𝜏𝑠+1 Hence, 𝐺c 𝑠 𝐺 𝑠 is a type − 1 system. Hence, for a step input, 𝑒ss = 0 For ramp input, 𝑒ss = 𝐴 𝐾v where 𝐾v = lim 𝑠→0 𝑠𝐺c 𝑠 𝐺 𝑠 = 𝐾𝐾2.
- 64. 63 Robot Steering System,PI Control Example Same system: 𝐺 𝑠 = 1 𝑠+2 = 0.5 0.5𝑠+1 Proportional plus Integral control, 𝐺c 𝑠 = 𝐾1 + 𝐾2 𝑠 = 𝐾1𝑠+𝐾2 𝑠 . Choose 𝐾1 = 18 and 𝐾2 = 20. Now since 𝐺c 𝑠 𝐺 𝑠 is type − 1: - Zero steady-state error for a step, - Finite steady-state error for a ramp. In this example, 𝐾v = 𝐾𝐾2 = 10 The steady-state error for a ramp input will be 1 𝐾v = 10 % of the slope of the ramp. For a unit ramp the steady-state error will be 0.1
- 65. 64 Left: 𝑦 𝑡for unit step input, 𝑟 𝑡 = 𝑢 𝑡 Right: 𝑦 𝑡 for unit ramp input, 𝑟 𝑡 = 𝑡𝑢 𝑡
- 66. 65 Robot Steering System,PI-Plus-Double Integral (PI2I) Control 𝐺c 𝑠 Controller 𝑌 𝑠 Actual Heading Angle + − 𝑅 𝑠 Desired Heading Angle Figure 32 𝐺 𝑠 = 𝐾 𝜏𝑠 + 1 Vehicle Dynamics Let’s examine a PI-plus-double integral controller: 𝐺c 𝑠 = 𝐾1 + 𝐾2 𝑠 + 𝐾3 𝑠2 = 𝐾1𝑠2 + 𝐾2𝑠 + 𝐾3 𝑠2 When 𝐾3 ≠ 0, 𝐺c 𝑠 𝐺 𝑠 = 𝐾 𝐾1𝑠2+𝐾2𝑠+𝐾3 𝑠2 𝜏𝑠+1 Hence, 𝐺c 𝑠 𝐺 𝑠 is a type − 2 system. Hence, for a step input or a ramp input, 𝑒ss = 0 For parabolic input, 𝑒ss = 𝐴 𝐾a where 𝐾a = lim 𝑠→0 𝑠2 𝐺c 𝑠 𝐺 𝑠 = 𝐾𝐾3.
- 67. 66 Robot Steering System,PI2I Control Example Same system: 𝐺 𝑠 = 1 𝑠+2 = 0.5 0.5𝑠+1 Proportional plus Integral plus Double Integral control, 𝐺c 𝑠 = 𝐾1 + 𝐾2 𝑠 + 𝐾3 𝑠2. Choose 𝐾1 = 18, 𝐾2 = 20 and 𝐾3 = 20. Now since 𝐺c 𝑠 𝐺 𝑠 is type − 2: - Zero steady-state error for a step or a ramp, - Finite steady-state error for a parabola. In this example, 𝐾a = 𝐾𝐾3 = 10 The steady-state error for a parabolic would be 1 𝐾v = 10 % of the curvature of the parabola. For a unit parabola the steady-state error will be 0.1
- 68. 67 Left: 𝑦 𝑡for unit step input, 𝑟 𝑡 = 𝑢 𝑡 Right: 𝑦 𝑡 for unit ramp input, 𝑟 𝑡 = 𝑡𝑢 𝑡
- 69. 68 𝑦 𝑡 forunit step input, 𝑟 𝑡 = 𝑢 𝑡 , extended time scale.
- 70. 69 𝑦 𝑡 forunit parabolic input, 𝑟 𝑡 = 𝑡2 𝑢 𝑡 . For this slide only, the gains have been reduced to illustrate the effects, 𝐾1 = 1.8, 𝐾2 = 0.2, 𝐾3 = 0.02
- 71. 70 Transient Responses AndPoles Should we have been able to predict transient responses from pole (and zero) positions ? Return to case of 𝐾1 = 18, 𝐾2 = 𝐾3 = 20
- 72. 71 Closed loop transferfunctions, 𝑇 𝑠 = 𝑌 𝑠 𝑅 𝑠 . P - one real pole, time constant = 1 20 = 0.05 s. PI - one real pole near the P one; plus another real pole (time constant ≈ 1 s) that is close to a zero. PI2I - one real pole near the P one; plus a conjugate pair with time constant ≈ 2 s, angle ≈ 60° , but near zeros.
- 73. 72 Step Responses To highlightthe impacts of the different poles, we have done a partial fraction expansion of the transfer function and used that to compute the step response. Control 𝑇 𝑠 = 𝑌 𝑠 𝑅 𝑠 Step Response, for 𝑡 ≥ 0 P = 18 𝑠 + 20 = 0.9 − 0.9e−20𝑡 PI = 18𝑠 + 20 𝑠2 + 20𝑠 + 20 ≅ 17.94 𝑠 + 18.94 + 0.0557 𝑠 + 1.056 ≅ 1 − 0.947e−18.94𝑡 − 0.053e−1.056𝑡 PI2I = 18𝑠2 + 20𝑠 + 20 𝑠3 + 20𝑠2 + 20𝑠 + 20 ≅ 17.89 𝑠 + 19 + 0.1106 𝑠 + 0.5578 𝑠2 + 0.9971𝑠 + 1.0525 ≅ 1 − 0.942e−19𝑡 − 0.108e−0.498𝑡 sin 0.897𝑡 + 2.57 Notes: - 10 % steady state error in the P case; it is zero in other cases. - Second term for each system has a similar decay rate (similar pole positions). - Third term in PI case decays much more slowly; third term in PI2I case even slower (small real parts of theses poles). - Terms related to poles that are near zeros have comparatively small magnitudes.
- 74. 73 Summary: Desirable Properties 𝐺c𝑠 Controller 𝑌 𝑠 + − 𝑅 𝑠 𝐸a 𝑠 Figure 33 𝐺 𝑠 Process 𝐻 𝑠 Sensor + + 𝑇d 𝑠 + + 𝑁 𝑠 With 𝐻 𝑠 = 1, 𝐸 𝑠 = 𝑅 𝑠 − 𝑌 𝑠 , 𝐿 𝑠 = 𝐺c 𝑠 𝐺 𝑠 , 𝐸 𝑠 = 1 1 + 𝐿 𝑠 𝑅 𝑠 − 𝐺 𝑠 1 + 𝐿 𝑠 𝑇d 𝑠 + 𝐿 𝑠 1 + 𝐿 𝑠 𝑁 𝑠 - Stability. - Good tracking in the steady state. - Good tracking in the transient. - Good disturbance rejection (good regulation). - Good noise suppression. - Robustness to model mismatch.
- 75. 74 Rest of course:About developing analysis and design techniques to address these goals. - Routh-Hurwitz Enables us to determine stability without having to find the poles of the denominator of a transfer function. - Root Locus Enables us to show how the poles move as a single design parameter (such as an amplifier gain) changes. - Bode diagrams There is often enough information in the Bode diagram of the plant/process to construct a highly effective design technique. - Nyquist diagram More advanced analysis of the frequency response that enables stability to be assessed even for complicated systems. Plan: Analysis And Design Techniques
- 76. 75 References (1) Tim Davidson,Introduction to Linear Control Systems, McMaster University, 2018.