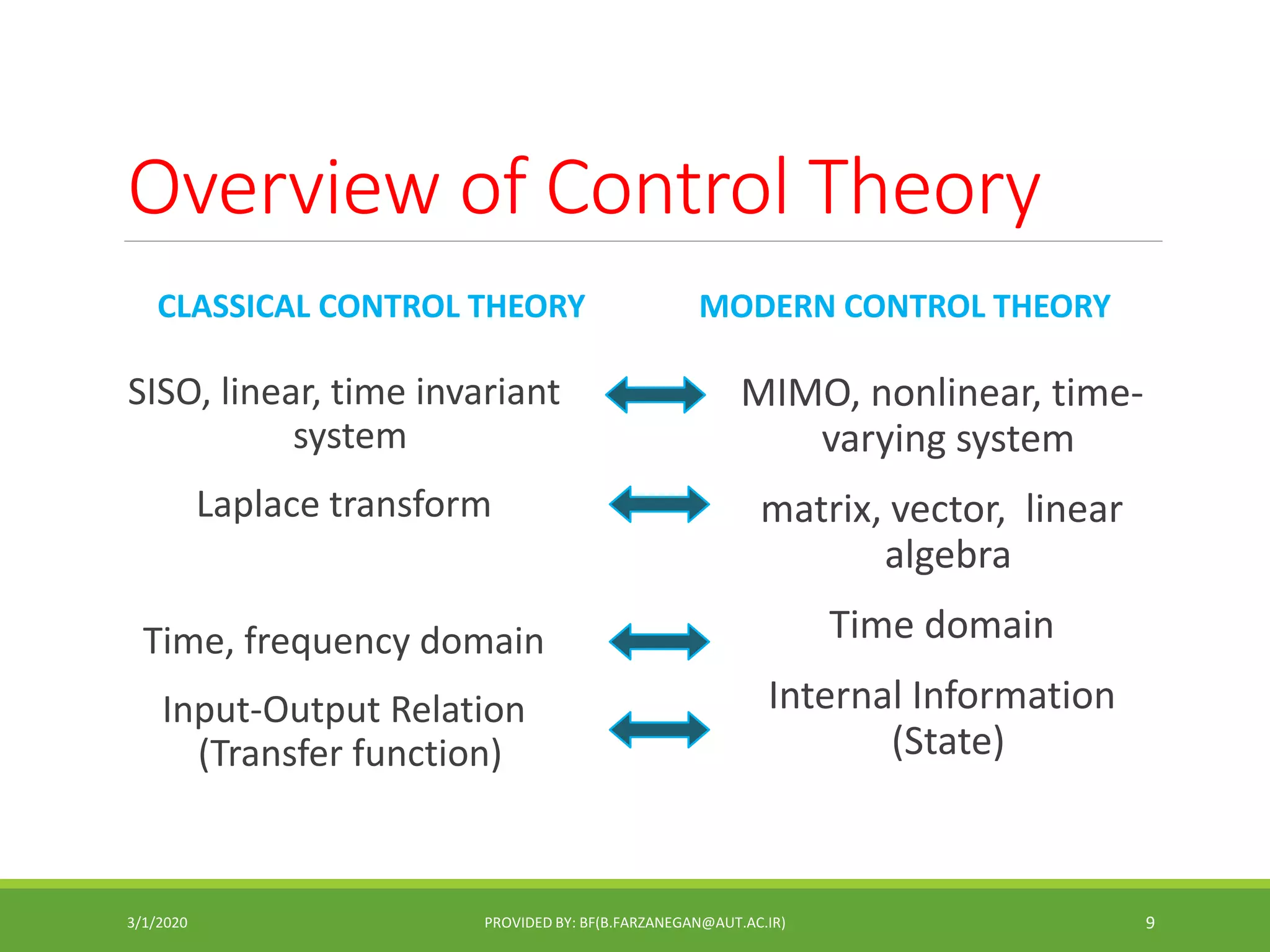
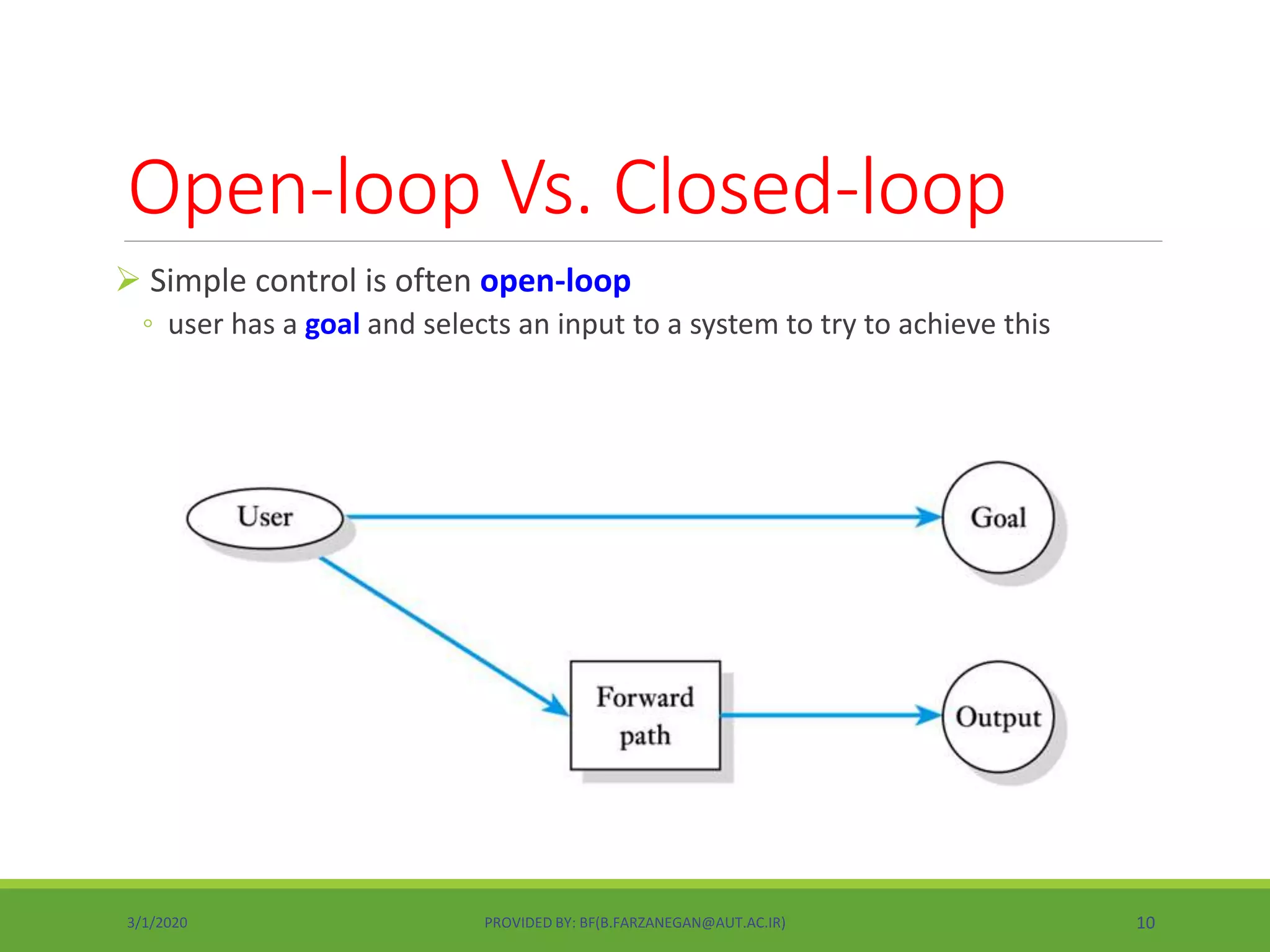
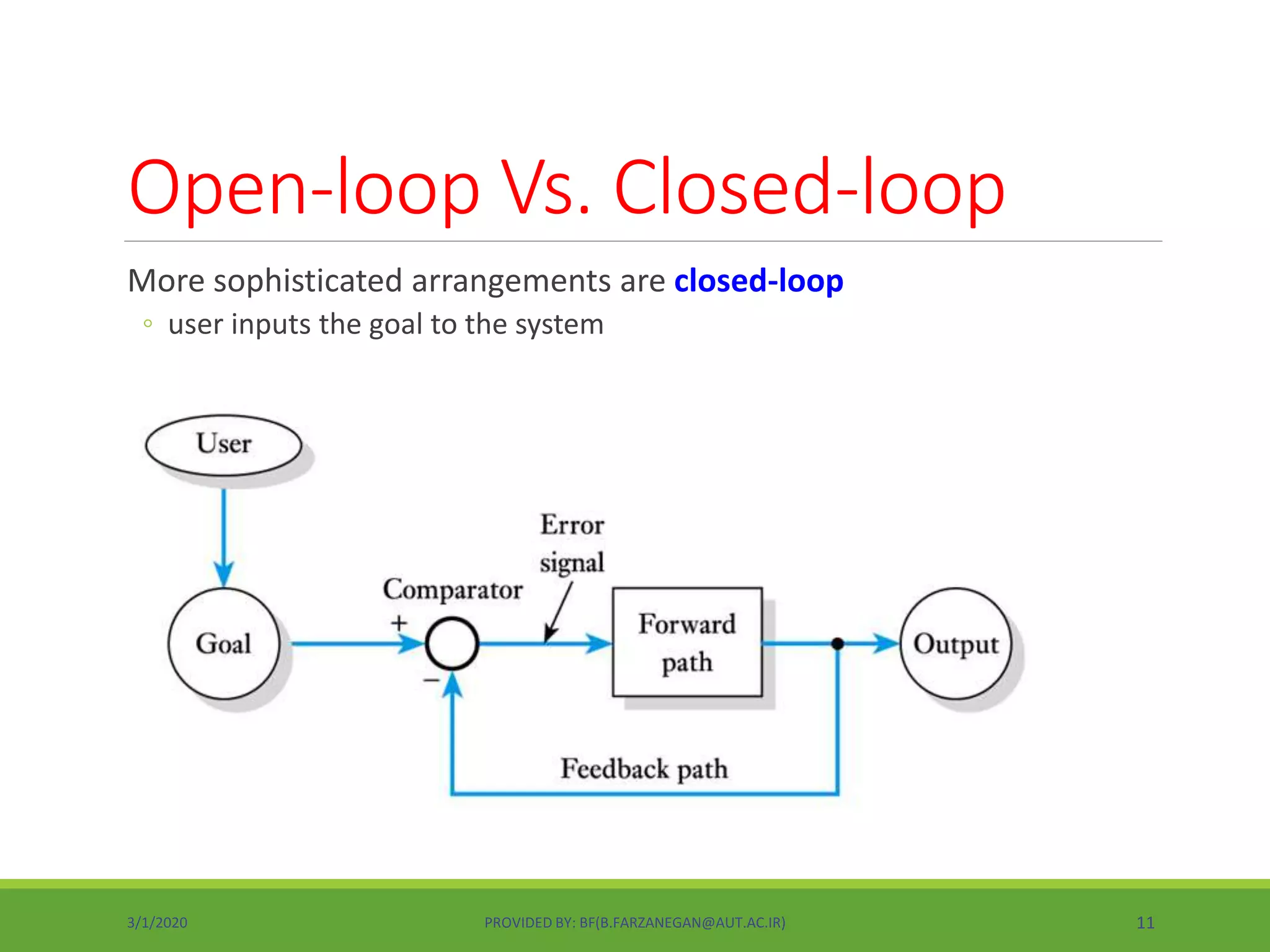
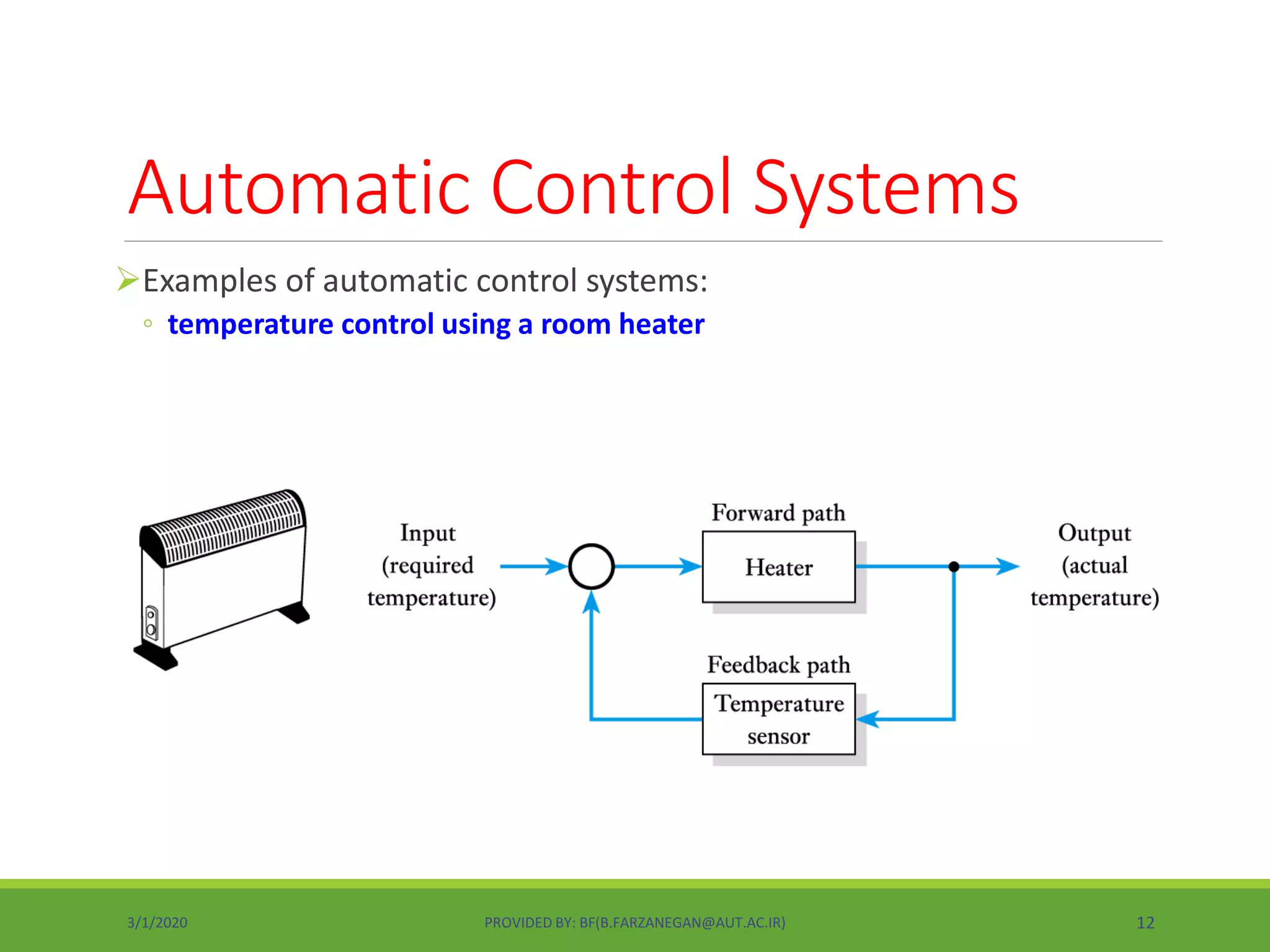
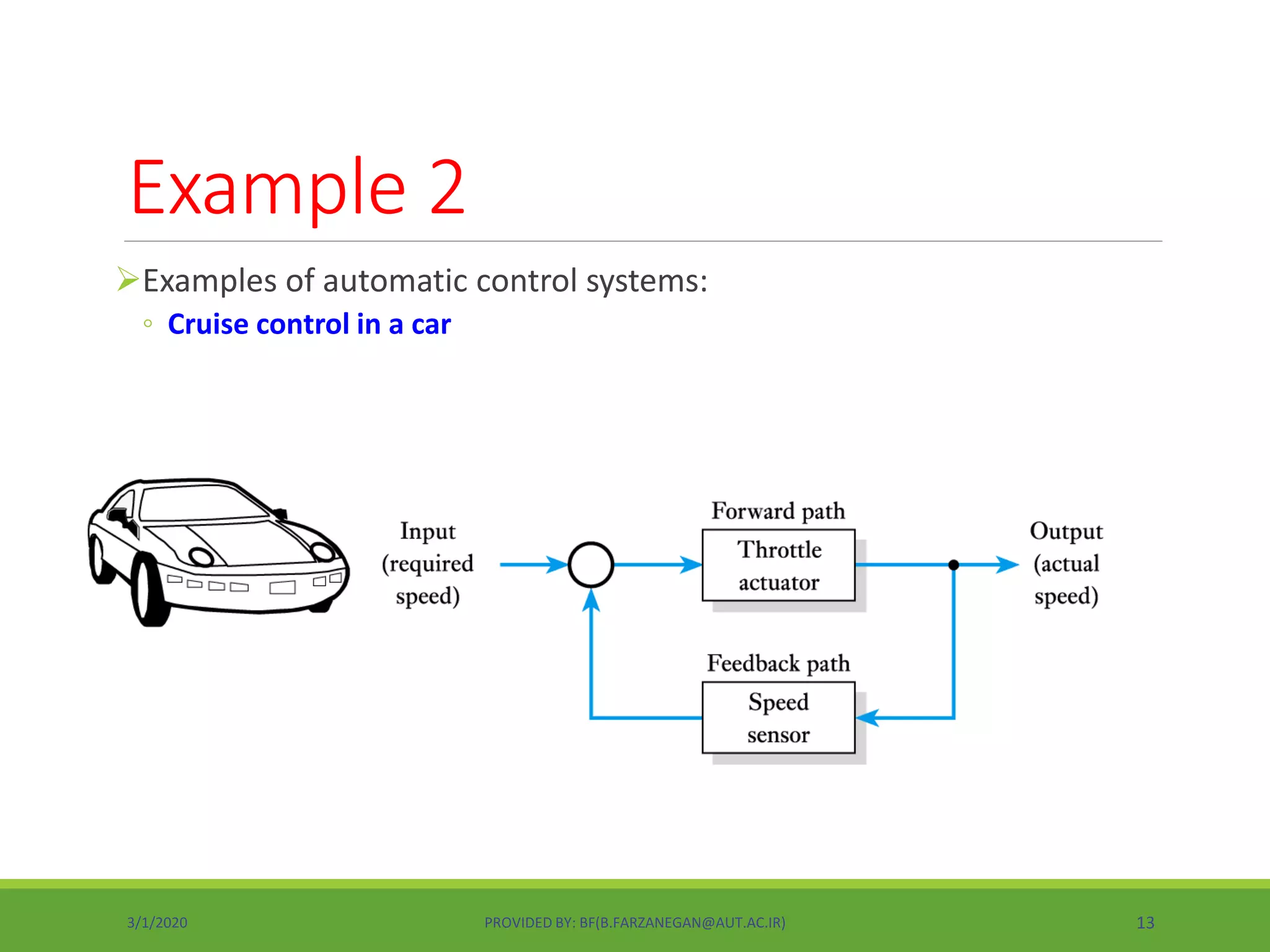
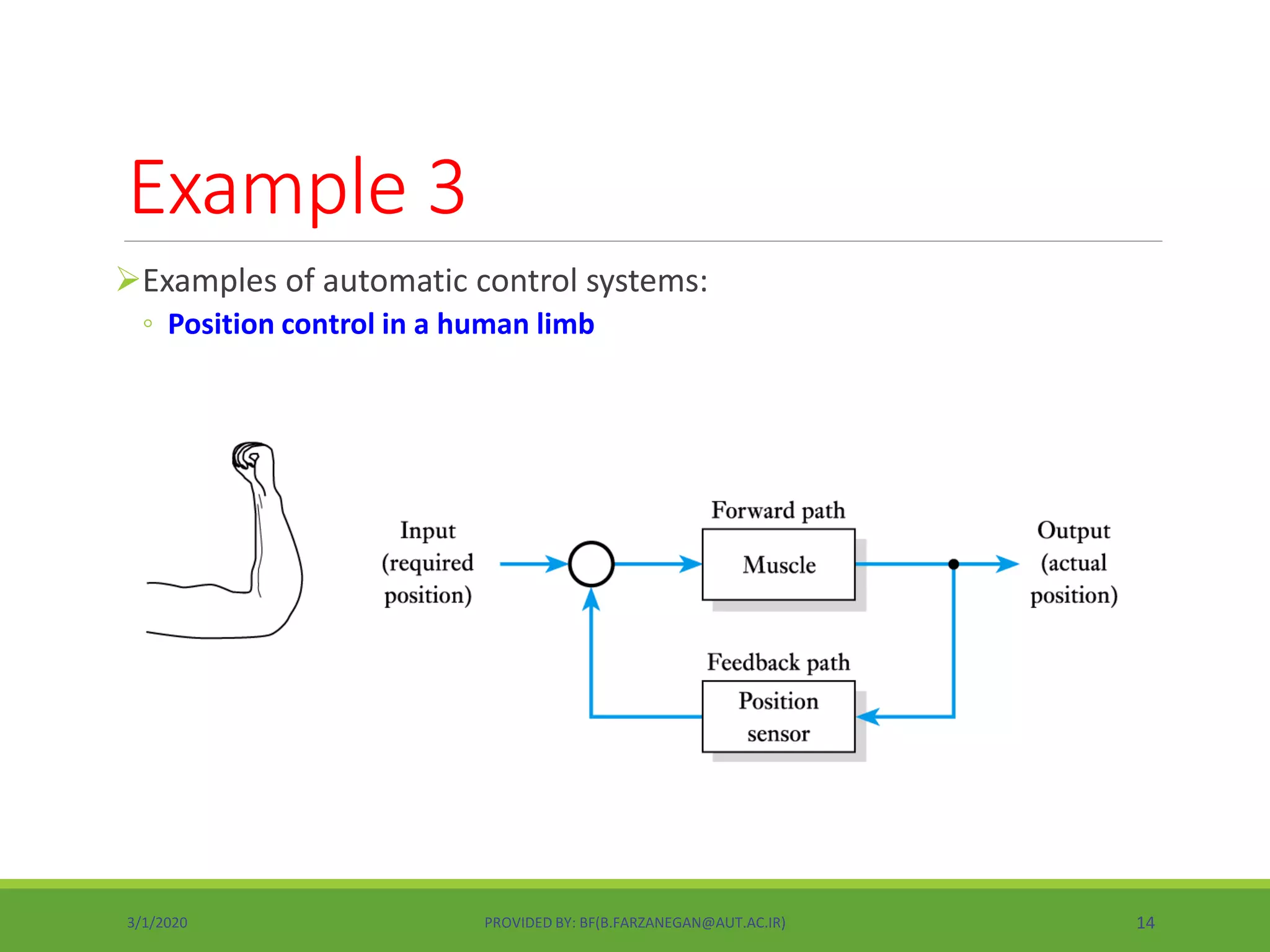
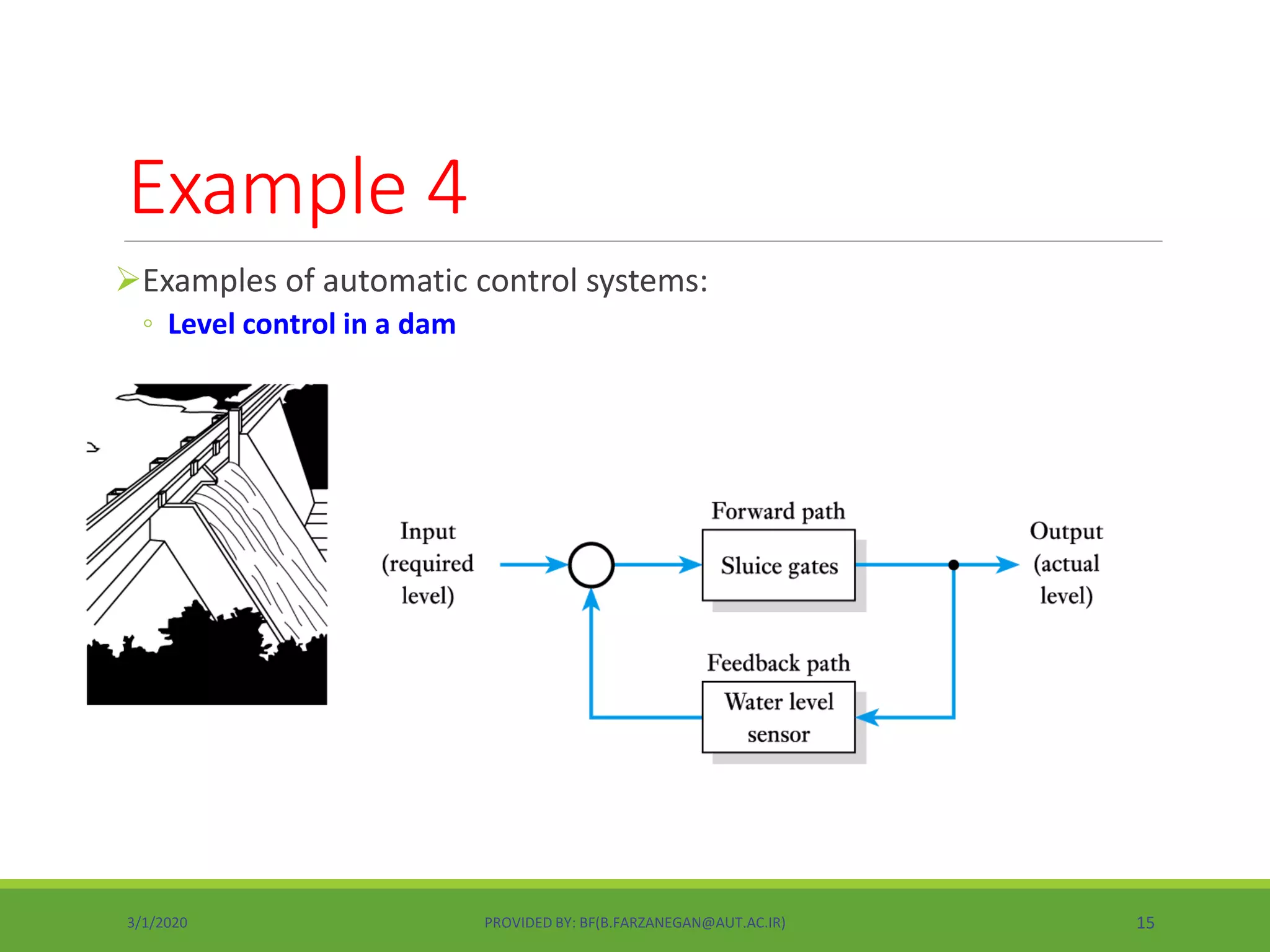
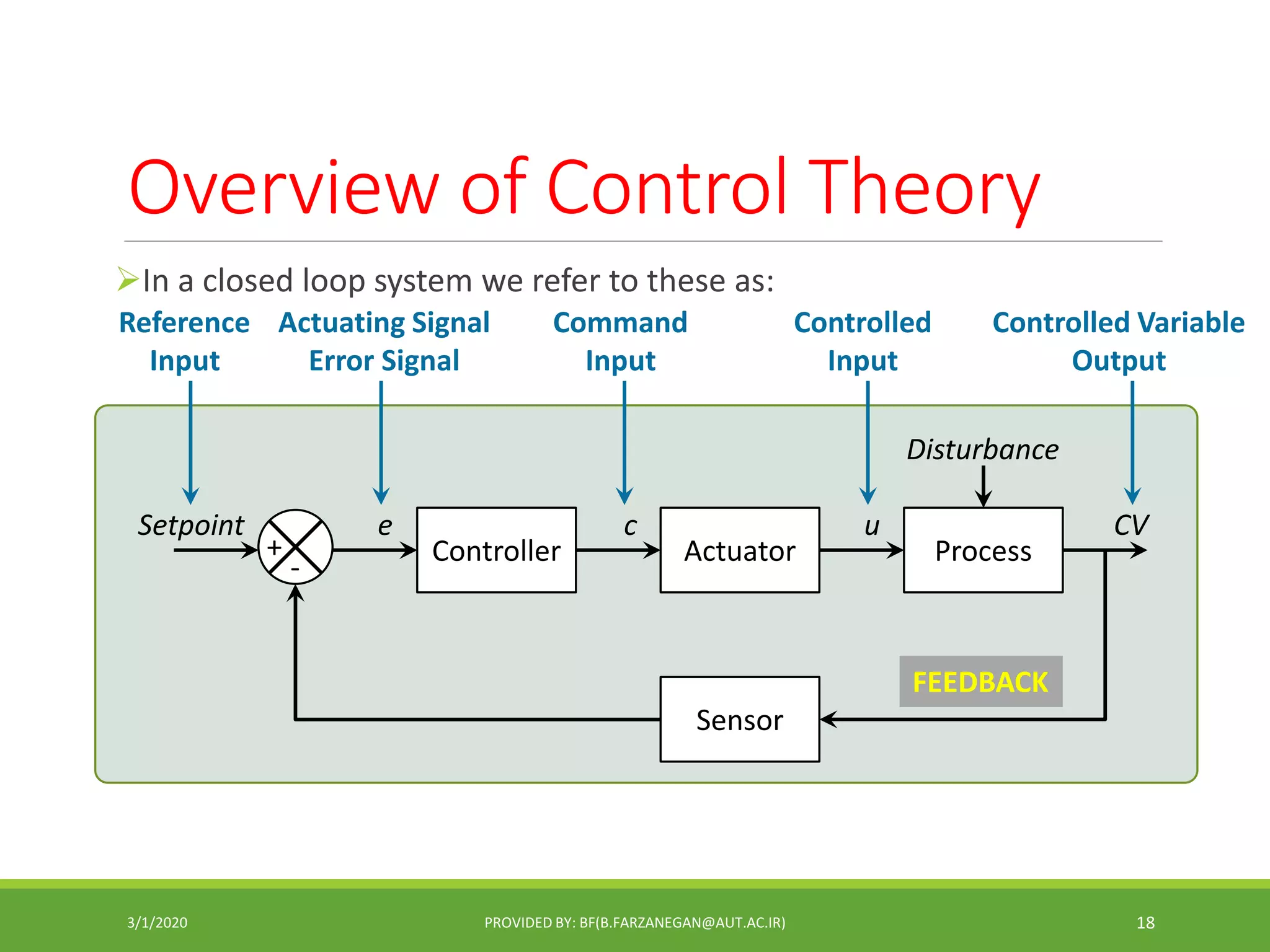
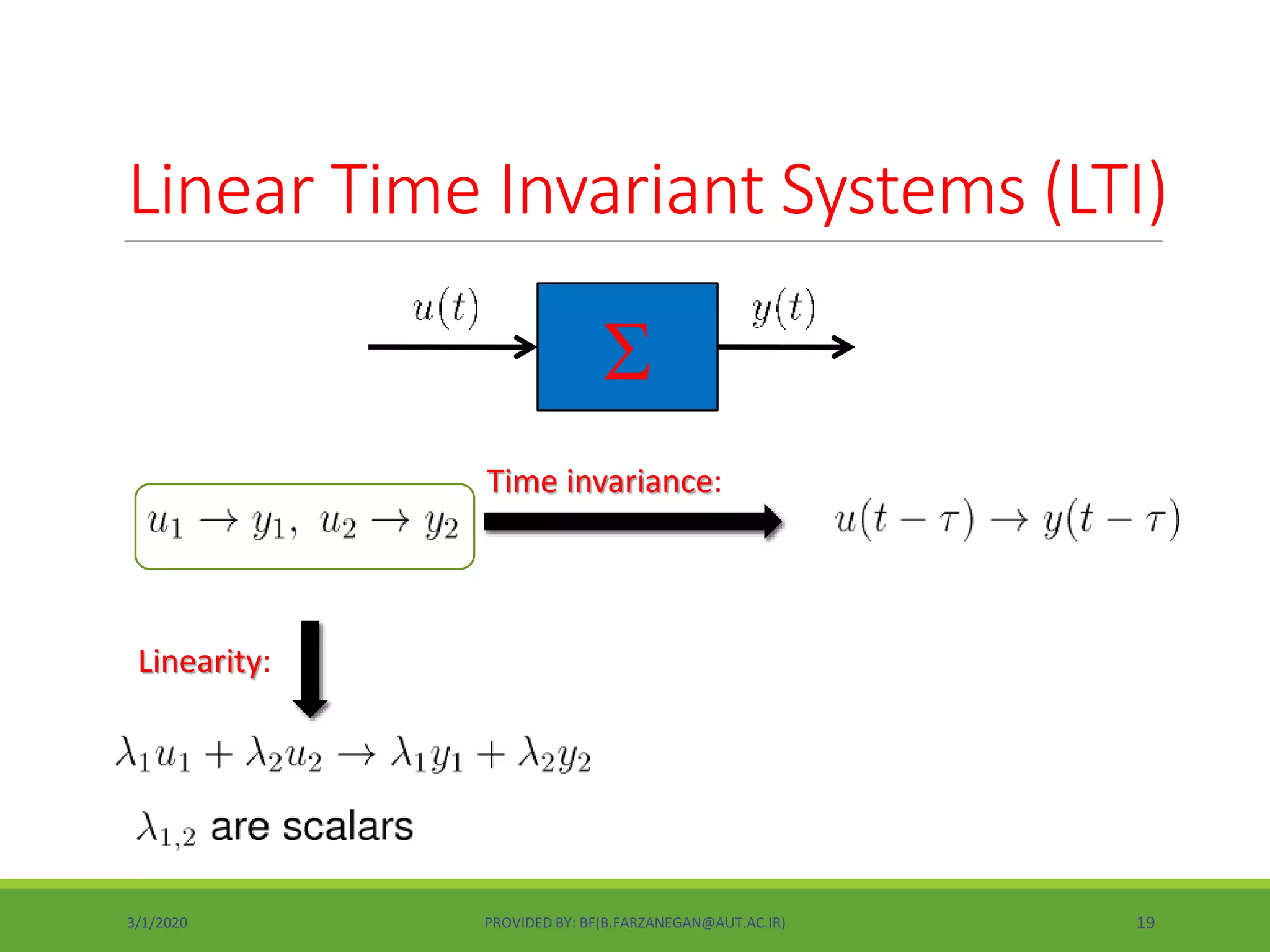
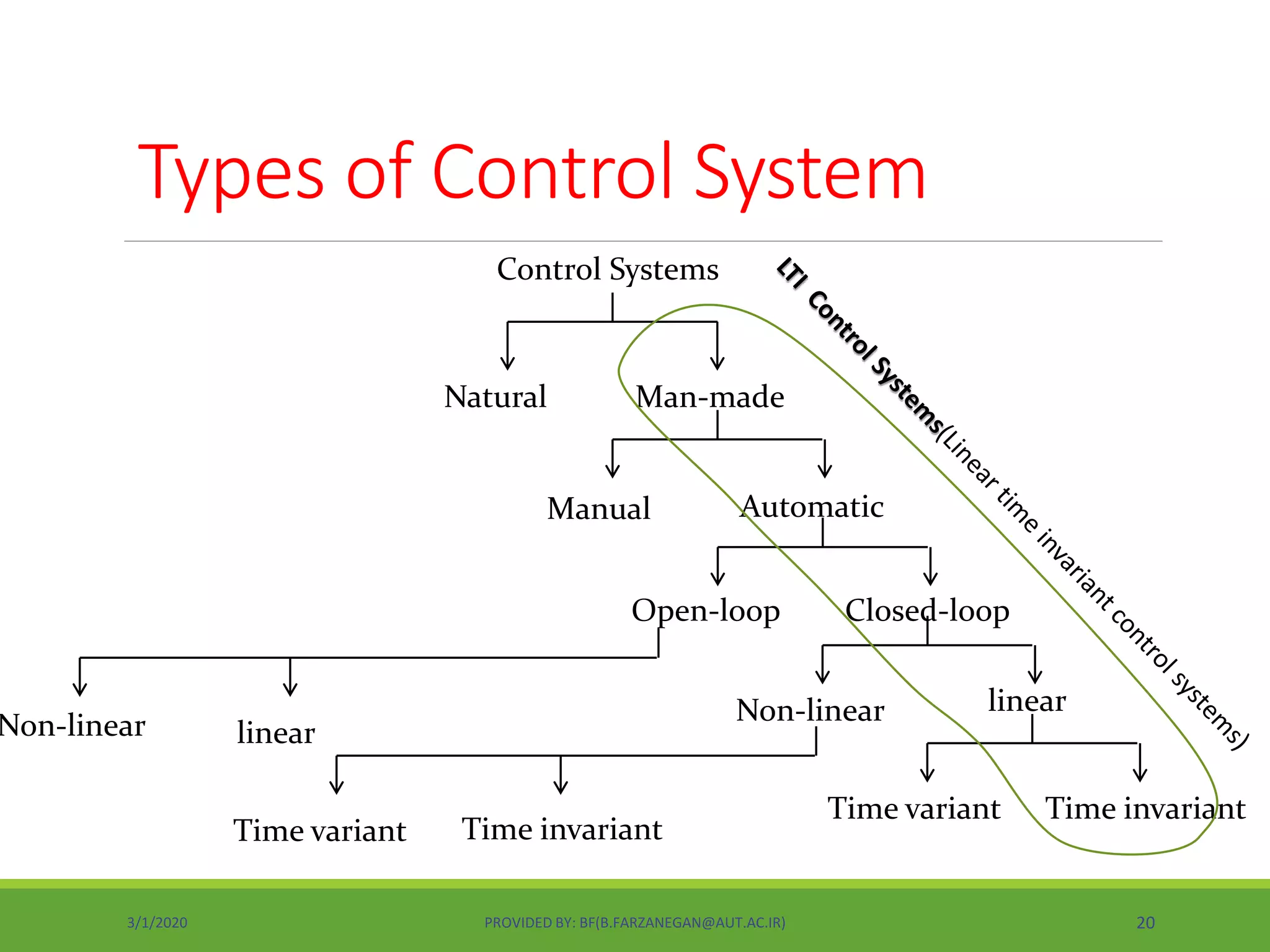
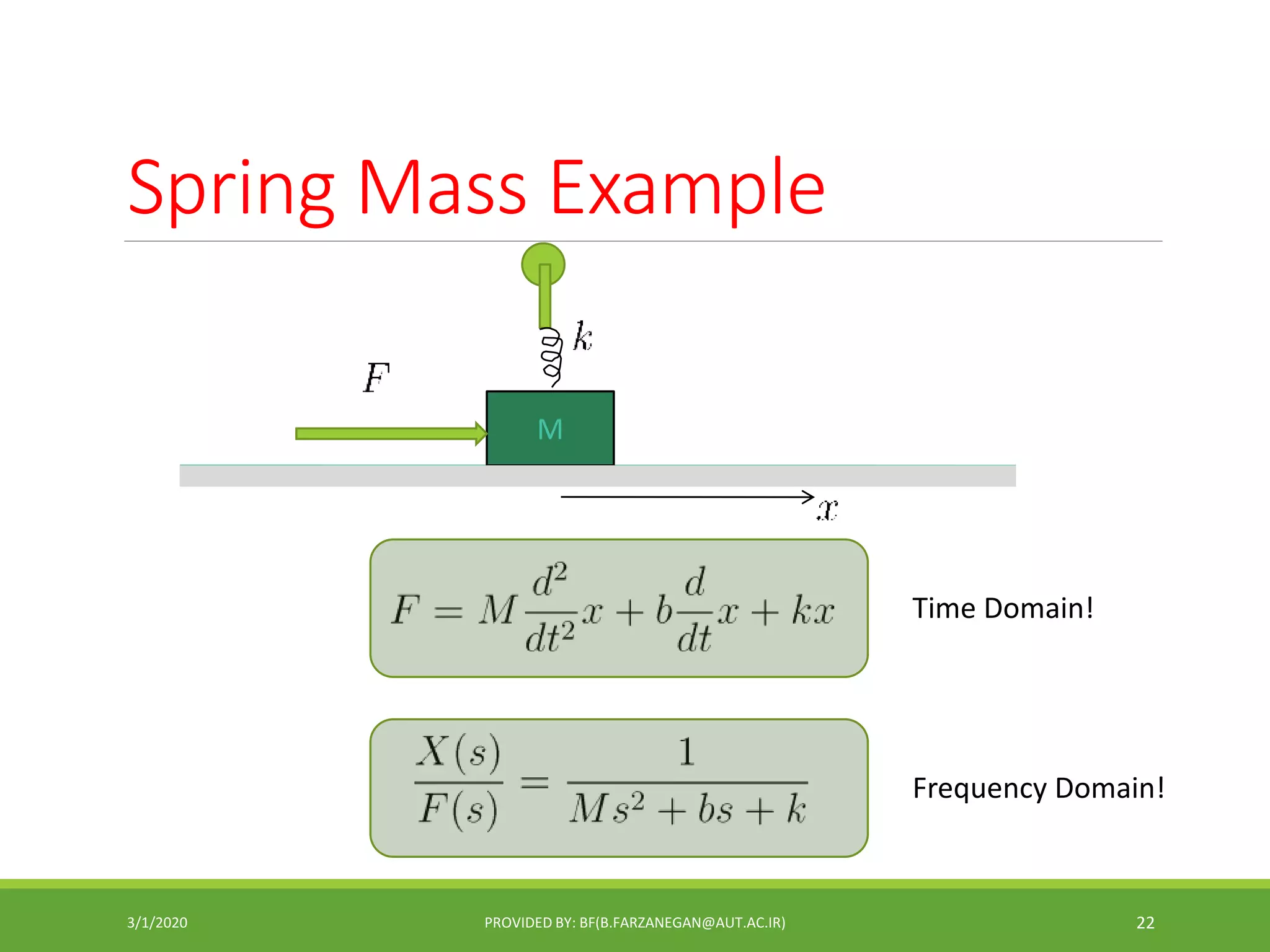
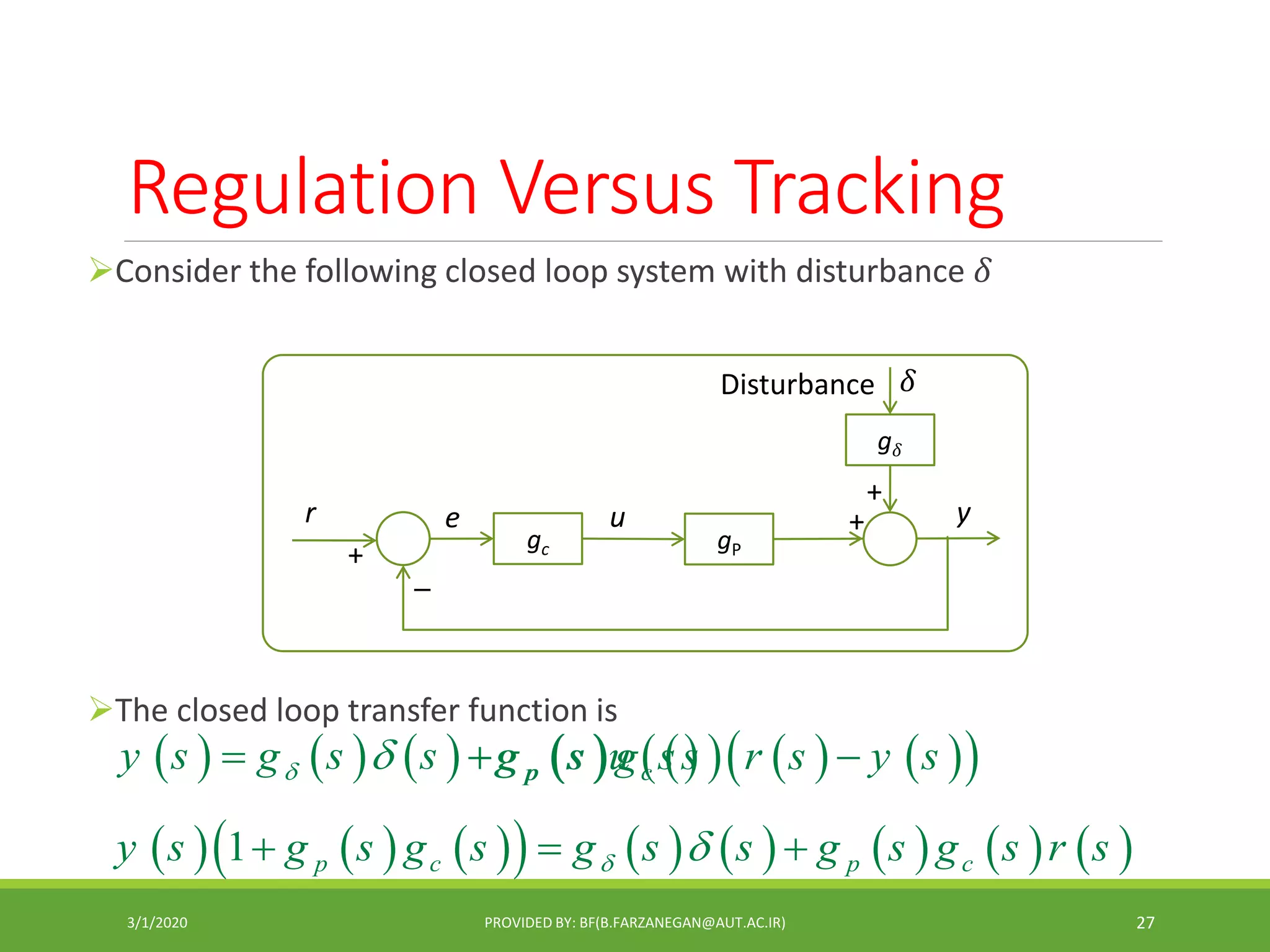
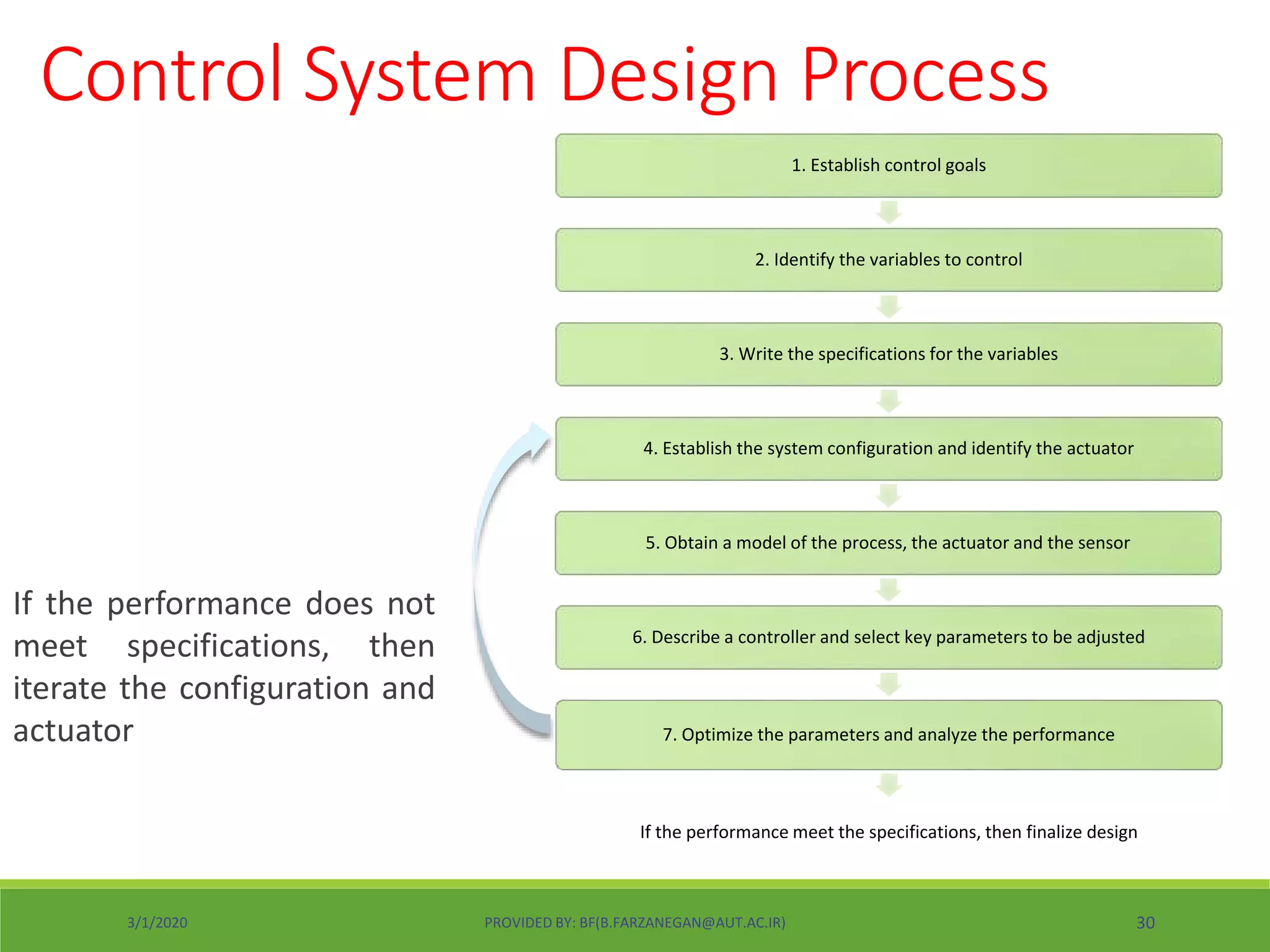
This document provides an overview of control systems and control theory. It discusses topics like stability, controller design using root locus and frequency response, PID controllers, different control structures, and performance requirements. The document is a lecture introduction that outlines key concepts in control systems including open-loop vs closed-loop control, regulation vs tracking problems, and the process of control system design and compensation.