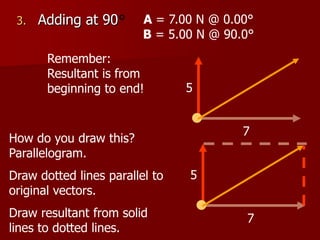
Vectors have both magnitude and direction, while scalars have only magnitude. Vectors are represented by arrows and their magnitude and direction can be shown using coordinate axes. Vectors can be added or subtracted by using the parallelogram method or by calculating the resultant vector's magnitude and direction. Components break vectors down into orthogonal x and y components to allow vectors to be added that are not at right angles.

1. Vector vs. Scalar
Vector Ex. Force
 magnitude & direction Weight
(amount)
Velocity
Scalar Acceleration
 magnitude Ex. Mass
Time
Money
Distance

2. Vector logistics
Vectors are represented by an arrow
Tells
direction
Length tells magnitude
Coordinate axis are used to represent position
North 10 N @ 45
+y 90°
180° +x
West -x East
0°
270° -y
South
Vectors are the same no matter where they are located, as long
as the magnitude and direction are the same!

3. Resultant
 a single vector that replaces two or more vectors
1. Adding vectors A = 5.00 N @ 0.00°
5 B = 7.00 N @ 0.00°
7 R = 12.0 N @ 0.00°
2. Subtracting vectors A = 5.00 N @ 0.00°
(special case of addition) B = 7.00 N @ 180°
5
7
A + B = 5 + -7 = -2 or R = 2.00 N @ 180°

5. 3. Adding at 90 A = 7.00 N @ 0.00°
B = 5.00 N @ 90.0°
Remember:
Resultant is from
beginning to end! 5
7
How do you draw this?
Parallelogram.
Draw dotted lines parallel to 5
original vectors.
Draw resultant from solid 7
lines to dotted lines.

6. How do you calculate the resultant?
Magnitude 
Pythagorean theorem
5
Direction 
SOHCAHTOA
2 2 opp 7
R 5 7 8.60N tan
adj
theta
Is the angle in  first
5
reference to the tan 1
inside
origin? If not, add 7 angle you
back to 0. 35.5 come to
from 0

7. yt. M = 54.0 N @ 10.0°
O = 35.0 N @ 100° R
35
2 2 54
R 54 35 64.4N Steps:
opp
tan 1.
adj
35 2. draw a picture
1
tan
54 3. pythagorean theorem
32.9 +10 = 42.9° 4. inverse tangent
5. add angle back to zero

8. Components
Components  2 vectors that replace 1 vector
1 is always on the x – axis M My
1 is always on the y – axis
A Mx
Ay yt Px
Cx
Py P
Ax C Cy
Components are always at right angles.
Components are independent of each other!

9. A = 87.0 m/s @ 40.0
How do you mathematically find Ay & Ax?
opp
SOHCAHTOA cos
adj sin
adj
hyp
Set angle theta. cos 40
Ax sin(40)
Ay
87 87
Ax 87 cos 40 Ay 87 sin(40)
A
Ay When finding components, it
will always be this way!
Ax = mag cos (angle)
Ax
Ay = mag sin (angle)
y sin, because x is cos

11. Vectors: 90°
To add vectors that are not at 90° to each
other, the vectors must first be broken
into their components.
ex. A = 10.4 m/s @ 75°
B = 6.7 m/s @ 25° R
Ay
A
B
By
Ax
Bx

12. Steps:
1. components  find xtot & ytot
2. draw a picture
3. pythagorean theorem
4. inverse tangent
5. add angle back to zero

13. ex. A = 10.4 m/s @ 75°
B = 6.7 m/s @ 25°
Ax = 10.4 cos 75 = 2.69 Ay = 10.4 sin 75 = 10.0
Bx = 6.7 cos 25 = 6.07 By = 6.7 sin 25 = 2.83
xtot = 8.76 ytot = 12.83
ytot = 12.83
R= (8.762 + 12.832)
R R = 15.5
θ = tan-1 (12.83/8.76)
θ = 55.9°
θ
R = 15.5 m/s at 55.9°
Xtot = 8.76