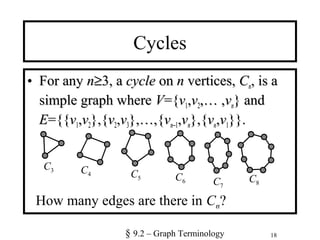
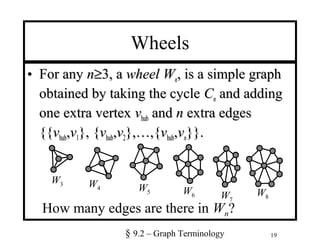
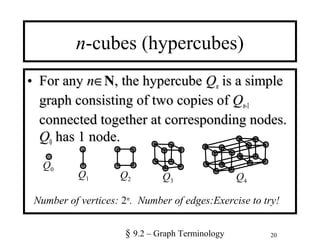
1. The document defines various types of graphs including simple graphs, multigraphs, pseudographs, directed graphs, and bipartite graphs. It discusses properties like vertices, edges, degrees, adjacency, and special graph structures like complete graphs, cycles, wheels, and n-cubes.
2. Key terms are defined, such as the degree of a vertex, adjacent vertices, and handshaking theorems for both undirected and directed graphs. Special graph structures including complete graphs, cycles, wheels, and n-cubes are also described.
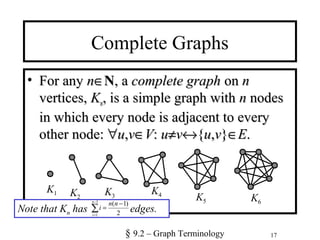
3. Bipartite graphs are introduced as simple graphs whose vertices can be partitioned into two disjoint sets such that every edge connects a vertex in one set to a

![2
§9.1: Graphs and Graph Models
• Correspond to symmetricCorrespond to symmetric
binary relationsbinary relations RR..
• AA simple graphsimple graph GG=(=(VV,,EE))
consists of:consists of:
– a seta set VV ofof verticesvertices oror nodesnodes ((VV corresponds tocorresponds to
the universe of the relationthe universe of the relation RR),),
– a seta set EE ofof edgesedges // arcsarcs // linkslinks:: unordered pairsunordered pairs ofof
[distinct?][distinct?] elementselements uu,,vv ∈∈ VV, such that, such that uRvuRv..
Visual Representation
of a Simple Graph
§ 9.1 – Graphs and Graph Models](https://image.slidesharecdn.com/graphtheory-150703201136-lva1-app6891/85/Graph-theory-2-320.jpg)



















![29
Adjacency Matrices
• MatrixMatrix AA=[=[aaijij], where], where aaijij isis 11 if {if {vvii,, vvjj} is an} is an
edge ofedge of GG,, 00 otherwise.otherwise.
a b
c d
0001
0011
0101
1110
a b
d c
0212
2110
1103
2030
§ 9.3 – Graph Representations & Isomorphism](https://image.slidesharecdn.com/graphtheory-150703201136-lva1-app6891/85/Graph-theory-29-320.jpg)
![30
Incidence Matrices
• MatrixMatrix AA=[=[aaijij]]vxe, where, where aaijij isis 11 ifif eejj incidentincident
withwith vvii,, 00 otherwise.otherwise.
b c
d
e
011010
000101
110000
101100
000011a
1
23
4
5
6
§ 9.3 – Graph Representations & Isomorphism](https://image.slidesharecdn.com/graphtheory-150703201136-lva1-app6891/85/Graph-theory-30-320.jpg)








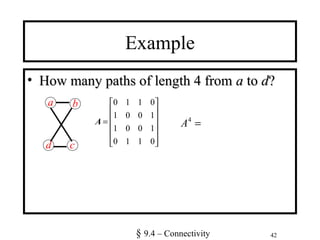
![41
Counting Paths w Adjacency Matrices
• LetLet AA be the adjacency matrix of graphbe the adjacency matrix of graph GG..
• TheThe numbernumber of paths of lengthof paths of length rr fromfrom vvii toto vvjj
is equal tois equal to ((AArr
))i,ji,j. (The notation (. (The notation (MM))i,ji,j denotesdenotes
mmi,ji,j where [where [mmi,ji,j] =] = MM..))
§ 9.4 – Connectivity](https://image.slidesharecdn.com/graphtheory-150703201136-lva1-app6891/85/Graph-theory-41-320.jpg)