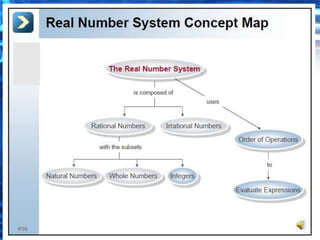
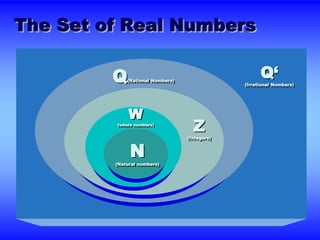
The document discusses sets and operations involving sets of real numbers. It defines key sets such as the real numbers, rational numbers, integers, natural numbers, whole numbers, and irrational numbers. It also covers properties of real numbers like closure, commutativity, associativity, distributivity, identity, and inverse properties as they relate to addition and multiplication. Examples are provided to illustrate set notation and properties. The document contains exercises asking to identify which properties justify certain statements involving real number operations.

1. Engr. Mexieca M. Fidel

2. THE REAL NUMBER
SYSTEM

3. WRITE SETS USING SET NOTATION
A set is a collection of objects called the
elements or members of the set. Set braces
{ } are usually used to enclose the
elements. In Algebra, the elements of a set
are usually numbers.
• Example 1: 3 is an element of the set {1,2,3} Note: This is referred
to as a Finite Set since we can count the elements of the set.
• Example 2: N= {1,2,3,4,…} is referred to as a Natural Numbers or
Counting Numbers Set.
• Example 3: W= {0,1,2,3,4,…} is referred to as a Whole Number
Set.

4. WRITE SETS USING SET NOTATION
A set is a collection of objects called the
elements or members of the set. Set braces
{ } are usually used to enclose the
elements.
• Example 4: A set containing no numbers is shown as { } Note: This
is referred to as the Null Set or Empty Set.
Caution: Do not write the {0} set as the null set. This set contains
one element, the number 0.
• Example 5: To show that 3 “is a element of” the set {1,2,3}, use the
notation: 3  {1,2,3}. Note: This is also true: 3  N
• Example 6: 0  N where  is read as “is not an element of”

5. WRITE SETS USING SET NOTATION
Two sets are equal if they contain
exactly the same elements. (Order
doesn’t matter)
• Example 1: {1,12} = {12,1}
• Example 2: {0,1,3}  {0,2,3}

6. In Algebra, letters called variables are
often used to represent numbers or to
define sets of numbers. (x or y). The
notation {x|x has property P}is an example of
“Set Builder Notation” and is read as:
{x  x has property P}
the set of all elements x such that x has a property P
• Example 1: {x|x is a whole number less than 6}
Solution: {0,1,2,3,4,5}
• Example 2: {x|x is a natural number greater than 12}
Solution: {13,14,15,…}

7. 1-1 Using a number line
-2 -1 0 1 2 3 4 5
One way to visualize a set a numbers
is to use a “Number Line”.
• Example 1: The set of numbers shown above includes
positive numbers, negative numbers and 0. This set is part of
the set of “Integers” and is written:
I = {…, -2, -1, 0, 1, 2, …}

8. 1-1 Using a number line
Graph of -1
o
1
2
11
4
o o
-2 -1 0 1 2 3 4 5
coordinate
Each number on a number line is called the
coordinate of the point that it labels, while the
point is the graph of the number.
• Example 1: The fractions shown above are examples of rational numbers. A
rational number is one than can be expressed as the quotient of two integers,
with the denominator not 0.

9. 1-1 Using a number line
Graph of -1
4 16
2 
o o o o o
-2 -1 0 1 2 3 4 5
coordinate
Decimal numbers that neither terminate nor
repeat are called “irrational numbers”.
• Example 1: Many square roots are irrational numbers, however some square
roots are rational.
• Irrational:
Rational:
2 7 
4 16
o
1
2
11
4
o o
7
Circumference
diameter
 

10. OPERATIONS INVOLVING SETS

20. REAL NUMBERS (R)
Definition:
REAL NUMBERS (R)
- Set of all rational and
irrational numbers.

21. SUBSETS of R
Definition:
RATIONAL NUMBERS (Q)
- numbers that can be expressed as
a quotient a/b, where a and b are
integers.
- terminating or repeating decimals
- Ex: {1/2, 55/230, -205/39}

22. SUBSETS of R
Definition:
INTEGERS (Z)
- numbers that consist of
positive integers, negative
integers, and zero,
- {…, -2, -1, 0, 1, 2 ,…}

23. SUBSETS of R
Definition:
NATURAL NUMBERS (N)
- counting numbers
- positive integers
- {1, 2, 3, 4, ….}

24. SUBSETS of R
Definition:
WHOLE NUMBERS (W)
- nonnegative integers
- { 0 }  {1, 2, 3, 4, ….}
- {0, 1, 2, 3, 4, …}

25. SUBSETS of R
Definition:
IRRATIONAL NUMBERS (Q´)
- non-terminating and non-repeating
decimals
- transcendental numbers
- Ex: {pi, sqrt 2, -1.436512…..}

26. The Set of Real Numbers
Q
Q‘
(Irrational Numbers)
Q
(Rational Numbers)
Z
(Integers)
W
(whole numbers)
N
(Natural numbers)

27. PROPERTIES of R
Definition:
CLOSURE PROPERTY
Given real numbers a and b,
Then, a + b is a real number (+),
or a x b is a real number (x).

28. PROPERTIES of R
Example 1:
12 + 3 is a real number.
Therefore, the set of reals is
CLOSED with respect to
addition.

29. PROPERTIES of R
Example 2:
12 x 4.2 is a real number.
Therefore, the set of reals is
CLOSED with respect to
multiplication.

30. PROPERTIES of R
Definition:
COMMUTATIVE PROPERTY
Given real numbers a and b,
Addition: a + b = b + a
Multiplication: ab = ba

31. PROPERTIES of R
Example 3:
Addition:
2.3 + 1.2 = 1.2 + 2.3
Multiplication:
(2)(3.5) = (3.5)(2)

32. PROPERTIES of R
Definition:
ASSOCIATIVE PROPERTY
Given real numbers a, b and c,
Addition:
(a + b) + c = a + (b + c)
Multiplication: (ab)c = a(bc)

33. PROPERTIES of R
Example 4:
Addition:
(6 + 0.5) + ¼ = 6 + (0.5 + ¼)
Multiplication:
(9 x 3) x 4 = 9 x (3 x 4)

34. PROPERTIES of R
Definition:
DISTRIBUTIVE PROPERTY of
MULTIPLICATION OVER
ADDITION
Given real numbers a, b and c,
a (b + c) = ab + ac

35. PROPERTIES of R
Example 5:
4.3 (0.11 + 3.02) = (4.3)(0.11) + (4.3)(3.02)
Example 6:
2x (3x – b) = (2x)(3x) + (2x)(-b)

36. PROPERTIES of R
Definition:
IDENTITY PROPERTY
Given a real number a,
Addition: 0 + a = a
Multiplication: 1 x a = a

37. PROPERTIES of R
Example 7:
Addition:
0 + (-1.342) = -1.342
Multiplication:
(1)(0.1234) = 0.1234

38. PROPERTIES of R
Definition:
INVERSE PROPERTY
Given a real number a,
Addition: a + (-a) = 0
Multiplication: a x (1/a) = 1

39. PROPERTIES of R
Example 8:
Addition:
1.342 + (-1.342) = 0
Multiplication:
(0.1234)(1/0.1234) = 1

40. EXERCISES
Tell which of the properties of real
numbers justifies each of the following
statements.
1. (2)(3) + (2)(5) = 2 (3 + 5)
2. (10 + 5) + 3 = 10 + (5 + 3)
3. (2)(10) + (3)(10) = (2 + 3)(10)
4. (10)(4)(10) = (4)(10)(10)
5. 10 + (4 + 10) = 10 + (10 + 4)
6. 10[(4)(10)] = [(4)(10)]10
7. [(4)(10)]10 = 4[(10)(10)]
8. 3 + 0.33 is a real number

41. TRUE OR FALSE
1. The set of WHOLE
numbers is closed
with respect to
multiplication.

42. TRUE OR FALSE
2. The set of NATURAL
numbers is closed with
respect to
multiplication.

43. TRUE OR FALSE
3. The product of any two
REAL numbers is a
REAL number.

44. TRUE OR FALSE
4. The quotient of any
two REAL numbers is a
REAL number.

45. TRUE OR FALSE
5. Except for 0, the set of
RATIONAL numbers is
closed under division.

46. TRUE OR FALSE
6. Except for 0, the set of
RATIONAL numbers
contains the
multiplicative inverse for
each of its members.

47. TRUE OR FALSE
7. The set of RATIONAL
numbers is associative
under multiplication.

48. TRUE OR FALSE
8. The set of RATIONAL
numbers contains the
additive inverse for
each of its members.

49. TRUE OR FALSE
9. The set of INTEGERS is
commutative under
subtraction.

50. TRUE OR FALSE
10. The set of INTEGERS
is closed with respect
to division.