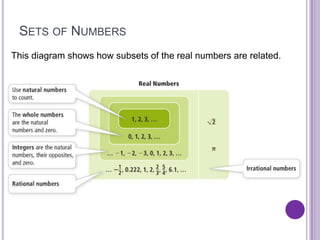
This document defines key concepts in algebra including variables, expressions, real numbers and their subsets. It discusses properties of real numbers such as additive inverses where the sum of a number and its opposite is 0, and multiplicative inverses where the product of a number and its reciprocal is 1. Examples are provided to illustrate these concepts and properties.

1. CHAPTER1: EXPRESSIONS,
EQUATIONS, AND INEQUALITIES
1.1 Patterns and Expressions
1.2 Properties of Real Numbers

2. DEFINITIONS
 A mathematical quantity is anything that can be
measured or counted.
 Quantities whose value stay the same are constants
 Quantities whose values change or vary are called
variable quantities

3. DEFINITIONS
 A variable is a symbol, usually a letter, that
represents one or more numbers.
 Examples: and
 A numerical expression is a mathematical phrase
that contains numbers and operation symbols.
 Examples: and
 An algebraic expression is a mathematical phrase
that contains one or more variables.
 Examples: and

4. SETS OF NUMBERS
 Real Numbers can be graphed on a number line and
contain several subsets
 Natural Numbers are the counting numbers:
1, 2, 3, 4, …
 Whole numbers are the natural numbers and zero
0, 1, 2, 3, 4 ….
 Integers are the positive and negative whole numbers and
zero

5. SETS OF NUMBERS
 Rational numbers are number that can be written as a
ratio of two integers (this includes fractions, terminating
decimals, and repeating decimals)
 Irrational Numbers cannot be written as a ratio of two
integers and have decimal representations that do not
terminate or repeat

6. SETS OF NUMBERS
This diagram shows how subsets of the real numbers are related.

7. EXAMPLE: CLASSIFY EACH NUMBER.

8. PROPERTIES OF REAL NUMBERS
 The properties of real numbers are relationships that are
true for all real numbers (except in one case, zero)
 The opposite (additive inverse) of any number a is –a.
 The Additive Inverse: The sum of a number and its opposite is
0.
 The reciprocal (multiplicative inverse) of any
nonzero number is
 The Multiplicative Inverse: The product of a number and its
reciprocal is 1

9. A set is closed with respect to an
operation if the operation can always be
completed with elements in the set.
Look for clues/key information:
• Does the equation contain 0 or 1?
• What is different about the left and right side of
the equation?

10. EXAMPLE: NAME THE PROPERTY ILLUSTRATED
BY EACH EQUATION.

