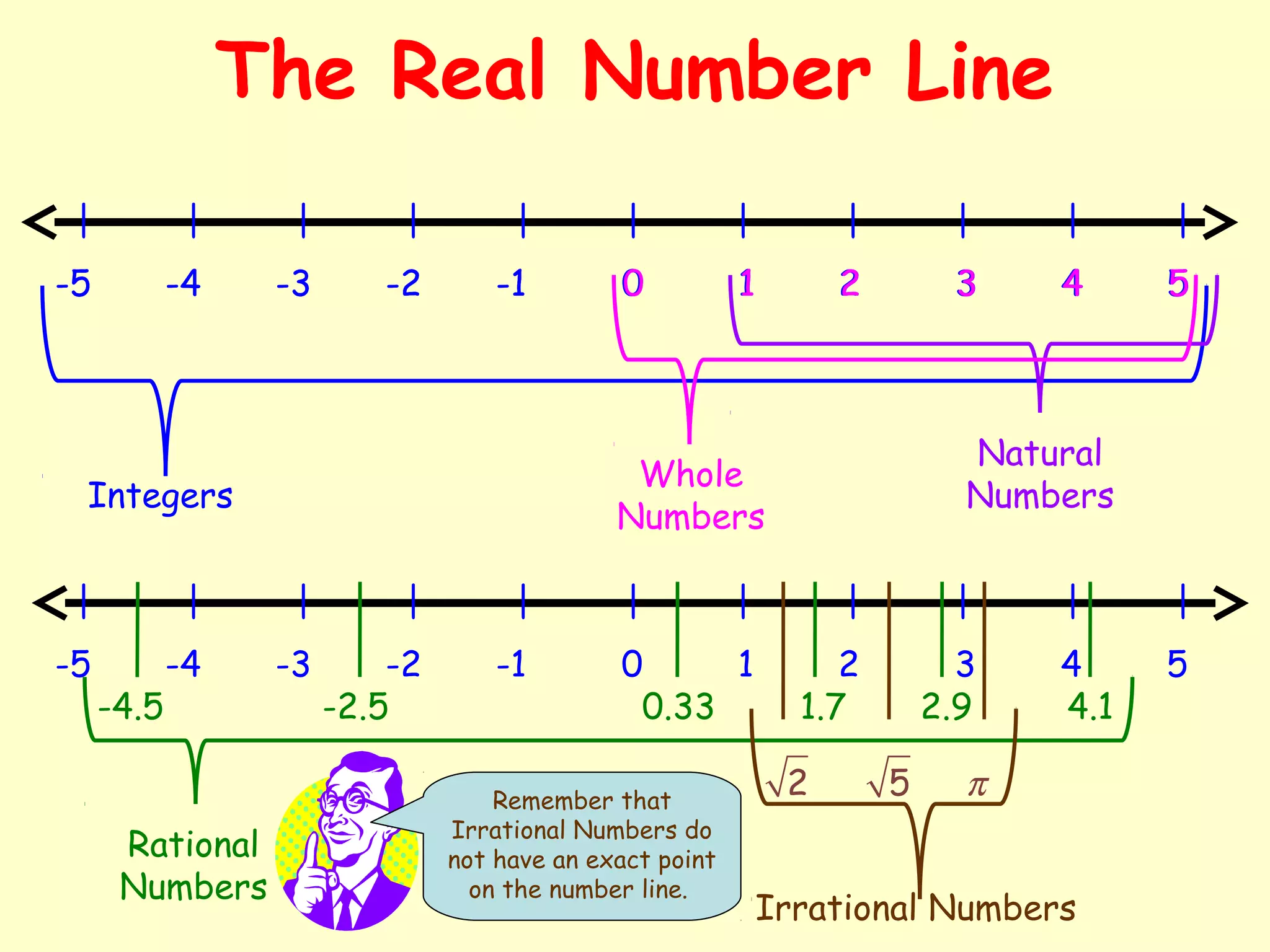
The document discusses the real number system and different types of real numbers. It defines rational numbers as numbers that can be written as a fraction a/b, and irrational numbers as numbers that cannot be written as a fraction, such as the square root of 2. It provides examples of evaluating square roots and comparing real numbers using inequality symbols. It also covers ordering numbers from least to greatest and expressing decimals as rational numbers or repeating decimals.

1. The Real Number System
Real Numbers
Rational Numbers
... -1.5, -1, -0.5, 0, 0.5, 1, 1.5, …
Integers
... -3, -2, -1, 0, 1, 2, 3, …
Whole Numbers
0, 1, 2, 3, 4, 5, 6, …
Natural Numbers
1, 2, 3, 4, 5, 6, …
... 2, 1.816, 0, 1, 2, ...π− −
Irrational
Numbers
2, 3, , 11...π

2. The Real Number Line
| | | | | | | | | | |
-5 -4 -3 -2 -1 0 1 2 3 4 5
Integers
-5 -4 -3 -2 -1 0 1 2 3 4 5
Natural
Numbers
-5 -4 -3 -2 -1 0 1 2 3 4 5
Whole
Numbers
| | | | | | | | | | |
-5 -4 -3 -2 -1 0 1 2 3 4 5
-4.5 -2.5 0.33 1.7 2.9 4.1
Rational
Numbers
2 5 π
Irrational Numbers
Remember that
Irrational Numbers do
not have an exact point
on the number line.

3. Square Roots
A number is a Perfect
Square if it is the product
of two Identical Factors.
• =6 6 36
• =10 10 100
• =2 2 4
− • =−5 5 25
− • =−7 7 49
These are all perfect
squares because they are
the product of two identical
factors.

4. Common Perfect Squares
Here is a list of the first 20 perfect
squares.
I should probably try to remember
those.

5. Evaluating Square Roots
Evaluate the following radicals
16 25 9 81
400 225 169 529
4 5 3 9
A number is a Perfect Square if it is
the product of two Identical Factors.
20 15 13 23

6. More Evaluating Radicals
121− 5.29±
16
81
2.89
12.25
−
−11 ±2.3
4
9
−
1.7
3.5
These are all Rational Numbers
15 20 90 80
3.87 4.47 9.49 8.94
These are all Irrational Numbers

7. More Irrational Roots
Irrational Roots will always fall
between two consecutive integers.
Between what two consecutive
integers is each square root?
35 130− 217
Between
5 and 6
Between
-12 and -11
Between
14 and 15
Asi De Facil That was easy
between
144 2& 1 1− −
between
25 & 36
between
196 & 225

8. Homework
Page 20: 10 – 22 & 28 - 36
Even Numbers Only

9. Expressing a Decimal as a
Rational Number
Write the fraction as
the given number over
the place value.
Reduce the resulting
fraction if possible.
0.3 0.225 0.2375 0.0325
3
10
225
1,000
9
40
2,375
10,000
19
80
325
10,000
13
400
A rational number is any number
that can be written in the form
a
b

10. Expressing Rational Numbers as a Decimal
A rational number is any number
that can be written in the form
Common Fractions Decimal Fractions
Written with a numerator
and a denominator.
1
2
3
4
1
16
To express as a decimal,
perform the division.
.5=
.75=
.0625=
The numerator is written after the decimal
point and the denominator is indicated by
the place value of the last digit.
0.5
0.75
0.0625
15
10 2
= =
75
10
3
0 4
= =
625
10,0 100
1
6
= =
These are all terminating
decimals.
a
b

11. Repeating Decimals
The same number, or pattern of numbers, repeats.
1
3
0.3333333333= 0.3=
2
3
0.6666666667= 0.6=
4
9
0.4444444444= 0.4=
2
11
0.1818181818= 0.18=
4
33
0.1212121212= 0.12=
8
33
0.2424242424= 0.24=
That was easy

12. Symbols of Inequality
Symbol Example Written in Words
> 9 2> 9 is greater than 2
< 2 9< 2 is less than 9
≥ 9 2≥ 9 is greater than
or equal to 2
≤ 2 9≤ 2 is less than or
equal to 9
≠ 2 9≠ 2 is not equal to 9

13. Comparing Real Numbers
Compare the following numbers with an inequality symbol.
17,
1
4
3
Write
each as a
decimal
4.1231, 4.3
Compare
the
decimals
4.1231 4.3<
Write the
answer with
the original
numbers
1
17 4
3
<
2
5
3
, 29
5.6 5., 3852
5.6 5.3852>
2
5 29
3
>
4
3
, 2
1.3 1., 4142
1.3 1.4142<
4
2
3
<
7
11
, 0.63
,0.63 0.63
0.63 0.63>
7
0.63
11
>

14. Ordering Numbers from
Least to Greatest
Order the numbers in each group from least to greatest.
3.2 3.002 3.02
3.002 3.02 3.2
2.021 2.21 2.0021− − −
2.21 2.021 2.0021− − −
5 3 2
5 5 5
12 4 3
5.416 5.75 5.6
1 7
2 5 2.4
2 4
− −
0.5 2 2.2361 1.75 2.4− −
2 1.75 0.5 2.2361 2.4− −
5 2 3
5 5 5
12 3 4
7 1
2 5 2.4
4 2
− −
5.416 5.6 5.75

15. Homework
Page 20: 38 - 50
Even Numbers Only