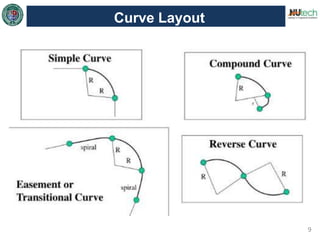
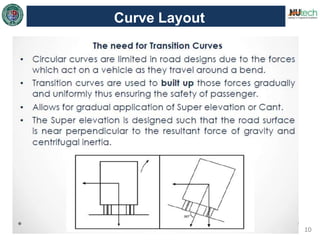
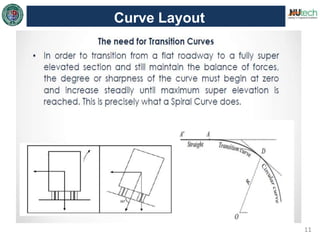
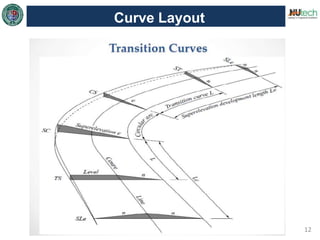
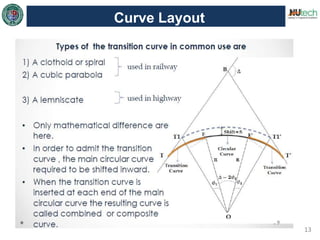
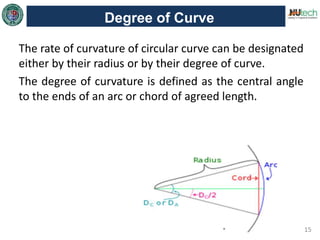
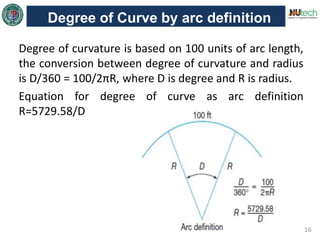
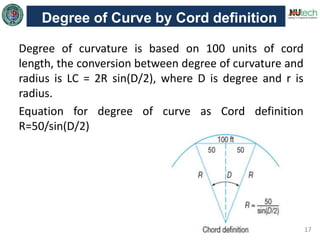
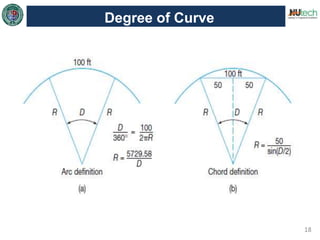
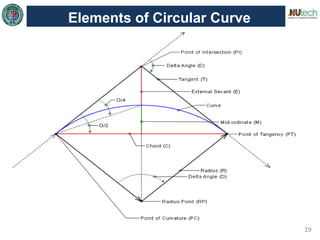
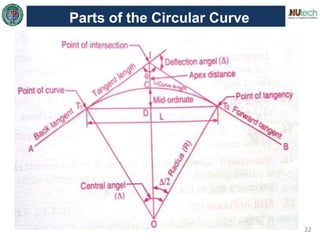
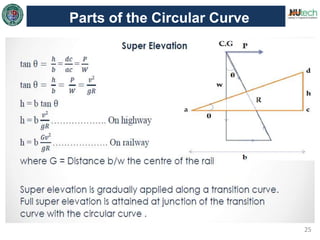
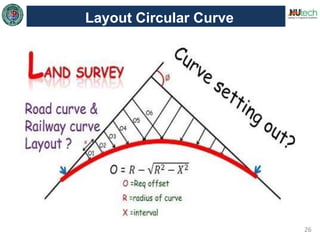
This document discusses horizontal curves in surveying. It covers the objectives of learning about horizontal curve layout, types of curves like simple, compound, and reverse curves. It defines degree of curve and how it is calculated based on the arc or cord length. It describes the elements of a circular curve like point of curvature, point of tangency, radius, chord length, and central angle. Methods for laying out a circular curve are discussed, including linear methods using offsets and bisection, and angular methods like Rankine's method and two theodolite method. Key questions about why curves are needed and defining the degree of curve are also answered.

1. 1
Horizontal Curves
Lec M Rizwan Shahid
Lec#03

2. 2
Key points of the previous lecture
Survey drafting and computation
 Area calculation
 Volume calculation

3. 3
Objectives of the current lecture
 To learn about the Horizontal curve layout
 Types of curves
 Degree of curve
 Superelevation
 Horizontal curve stakeout/ layout methods

4. 4
Curves
Curves are
provided whenever
a road, rail or other
civil engineering
projects changes
its direction from
right to left (vice
versa) or changes
its alignment from
up to down (vice
versa).

5. 5
Curve
There are two types of curves provided primarily for
the comfort and ease of the drivers in the road
namely:
Horizontal Curve
Vertical Curve

6. 6
Curve Layout
Horizontal Curves in Surveying
Horizontal curves are provided to change the
direction or alignment of a road.
Horizontal Curve are circular curves or circular
arcs.
 The sharpness of a curve increases as the radius
is decrease which makes it risky and dangerous.
The main design criterion of a horizontal curve is
the provision of an adequate safe stopping sight
distance.

7. 7
Curve Layout
Types of Horizontal Curve:
Simple Curve:
A simple arc provided in the road to impose a curve
between the two straight lines.
Compound Curve:
Combination of two simple curves combined
together to curve in the same direction.
Reverse Curve:
A reverse curve (or "S" curve) is a section of the
horizontal alignment of a highway or railroad route
in which a curve to the left or right is followed
immediately by a curve in the opposite direction.

8. 8
Curve Layout
Transition or Spiral Curve:
A curve that has a varying radius. Its provided with
a simple curve and between the simple curves in a
compound curve.
A transition curve may be defined as a curve of
varying radius of infinity at tangent point to a design
circular curve radius provided in between the
straight and circular path in order that the
centrifugal force was gradual. This is also known as
easement curve

9. 9
Curve Layout

10. 10
Curve Layout

11. 11
Curve Layout

12. 12
Curve Layout

13. 13
Curve Layout

14. 14
Degree of Curve
Degree of curve or degree of curvature is a measure
of curvature of a circular arc used in civil
engineering for its easy use in layout surveying.
We can determine the degree of any curve by first
finding the circumference of a circle.

15. 15
Degree of Curve
The rate of curvature of circular curve can be designated
either by their radius or by their degree of curve.
The degree of curvature is defined as the central angle
to the ends of an arc or chord of agreed length.

16. 16
Degree of Curve by arc definition
Degree of curvature is based on 100 units of arc length,
the conversion between degree of curvature and radius
is D/360 = 100/2πR, where D is degree and R is radius.
Equation for degree of curve as arc definition
R=5729.58/D

17. 17
Degree of Curve by Cord definition
Degree of curvature is based on 100 units of cord
length, the conversion between degree of curvature and
radius is LC = 2R sin(D/2), where D is degree and r is
radius.
Equation for degree of curve as Cord definition
R=50/sin(D/2)

18. 18
Degree of Curve

19. 19
Elements of Circular Curve

20. 20
Elements of the Circular Curve
• PC = Point of curvature.
• PT = Point of tangency
• PI = Point of intersection of the tangents.
• T = Length of tangent from PC to PI and from PI to
PT.
• R = Radius of simple curve, or simply radius.
• L = Length of chord from PC to PT.
• Lc = Length of curve from PC to PT.
• m = Middle ordinate, the distance from midpoint of
curve to midpoint of chord.
• Sub chord = chord distance between two adjacent
full stations.

21. 21
Elements of the Circular Curve
I = Intersection /central angle. It is the angle of
intersection of the tangents. The angle subtended by
PC and PT at O is also equal to I, where O is the center
of the circular curve.
x = offset distance from tangent to the curve. Note: x
is perpendicular to T.
θ = offset angle subtended at PC between PI and any
point in the curve
D = Degree of curve. It is the central angle subtended
by a length of curve equal to one station. In English
system, one station is equal to 100 ft.

22. 22
Parts of the Circular Curve

23. 23
Parts of the Circular Curve

24. 24
Parts of the Circular Curve

25. 25
Parts of the Circular Curve

26. 26
Layout Circular Curve

27. 27
Layout of Circular Curve
Methods of Setting out of single Circular curve
• Linear Methods
• Angular Methods.
1) Linear Methods
• By offsets or ordinate from the long chord
• By successive bisection of arcs or chords.
•By offsets from the tangents.
•By offsets from the chord produced.

28. 28
Layout of Circular Curve
2) Angular Method
• Used when length of curve is large
• More accurate than the linear methods
• Theodolite and Total Station is used
Deflection Angel/ Rankine method of tangential
angles OR One theodolite method
Two theodolite method
Coordinates

29. 29
Curve Layout
Q-1 Why we need to incorporate horizontal curve.
Ans:-
Horizontal curves are provided to change the direction
or alignment of a road

30. 30
Curve Layout
Q-2 What is degree of curve
Ans:-
The rate of curvature of circular curve can be
designated either by their radius or by their degree of
curve.
The degree of curvature is defined as the central angle
to the ends of an arc or chord of agreed length.
This angle is also the change in forward direction as
that portion of the curve is traveled.
Degree of curve or degree of curvature is a measure of
curvature of a circular arc used in civil engineering for
its easy use in layout surveying.

31. 31
Curve Layout
Q-3 Enlist the angular methods of curve layout
Ans:-
Rankine method of tangential angles OR One
theodolite method
Two theodolite method

32. 32
Topics covered in the lectures
 To learn about the Horizontal curve layout
 Types of curves
 Degree of curve
 Superelevation
 Layout of simple Curve and its method

33. 33