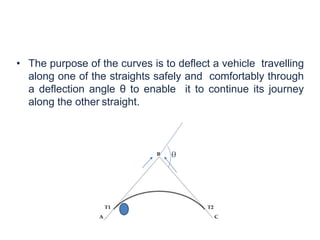
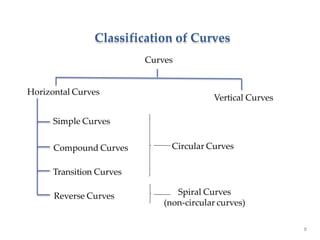
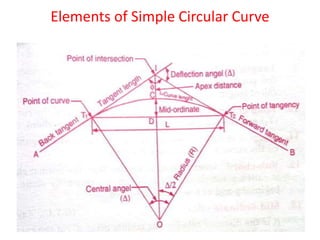
Curves are used to gradually change the direction of transportation routes like roads, railways and pipelines. They connect straight tangents and are usually circular arcs. There are different types of curves classified based on their shape and connection of tangents like simple, compound, reverse etc. Elements like radius, deflection angle, length of curve, tangent length etc are used to design circular curves. Various surveying methods like Rankine's, two theodolite etc are used to establish curves on the ground based on their elements and principles. Compound curves consist of two simple circular curves bending in the same direction and joining at a common point of compound.

1. CURVES

2. • Curves are usually employed in lines
of communication in order that the change in direction at
the intersection of the straight lines shall be gradual.
• The lines connected by the curves are tangent to it and
are called Tangents or Straights.
• The curves are generally circular arcs but parabolic arcs
are often used in some countries for this purpose.
• Most types of transportation routes, such as
highways, railroads, and pipelines, are connected by
curves in both horizontal and vertical planes.
Curves

3. • The purpose of the curves is to deflect a vehicle travelling
along one of the straights safely and comfortably through
a deflection angle θ to enable it to continue its journey
along the other straight.
θ

7. Necessity of Curves
• Straight route of road or track is always desirable, since it provides
economy in construction, transportation and maintenance. But
when there is change in alignment or gradient of road or track, then
it becomes a need to provide curves under following circumstances
• Excessive cutting and filling can be prevented by providing the
change in alignment by curves.
• The obstruction which came in the way of straight alignment can be
made easier by providing by pass with the help of curves
• In the straight route gradient are made more comfortable and easy
providing diversions with help of curves.
• In the straight route costly land comes in the way then it can
avoided by providing diversions with the help of curves

8. Horizontal Curves
Vertical Curves
Simple Curves
Compound Curves
Reverse Curves
Transition Curves
Circular Curves
Spiral Curves
(non-circular curves)
Classification of Curves
Curves
8

9. Classification of Curves
1) Simple Curves: Consist of single circular curve Connecting two
straights. It is tangential to the two straights at the joining ends.
2) T1TT2 is a simple circular curve of radius R joining two straights T1I
and T2I intersecting at I

10. Compound curves: Consist of 2 simple
circular curves of different radii, bending in
the same direction and lying on the same
sides of their common tangents, their
centres being on the same side of the
curve.

11. Reverse curves: Consist of 2 simple
circular curves of equal or unequal radii,
bending in opposite direction with common
tangent at their junction (meeting Point),
their center lying on the opposite sides of
the curve. Also known as Serpentine Curve
or S -curve

12. Transition Curves: Curve usually
introduced between a simple circular curve
and a straight or between two simple
curves. It is also known as easement
curve.
Combined Curves:
Combination of simple
circular and transition
curves . Generally
preferred in railways
and highways

13. Vertical Curves: Curves in vertical plane, used to join two
intersecting grade lines. The reduced level of these
curves change from point to point in a gradual and
systematic manner.
• A vertical summit curve is provided when a rising
gradient joins a falling gradient.
• A vertical sag curve is provided when a falling gradient
joins a rising gradient.

14. Elements of Simple Circular Curve

15. • Back tangent or First Tangent ‐ AT₁ – Previous to the curve
• Forward Tangent or Second tangent‐ B T₂‐ Following the
curve
• Point of Intersection ( P.I.) or Vertex. (v).If the tangents AT₁
and BT₂ .are produced they will meet in a point called the
point of intersection
• Point of curve ( P.C.) –Beginning Point T₁ of a curve. Alignment
changes from a tangent to curve.
• Point of Tangency ‐ PT – End point of curve ( T₂ )
• Intersection Angle (Ø ) -The Angle AVB between tangent AV
and tangent VB

16. • Deflection Angle (Δ ) - The angle at P.I. between tangent
AI and IB
• Tangent Distance/Length – It is the distance between
P.C. and P.I.
• External Distance/Apex Distance – CI - The distance from
the mid point of the curve to P.I
• Length of curve – l -It is the total length of curve from
P.C. to P.T.
• Long Chord – It is the chord joining P.C. to P.T., T₁ T₂ is a
long chord
• Normal Chord: A chord between two successive regular
station on a curve is called normal chord. Normally , the
length of normal chord is 1 chain ( 2o mt).

17. • Sub chord-The chord shorter than normal chord (
shorter than 20 mt) is called sub chord)
• Versed sine – Distance CD -The distance between
mid point of long chord ( D ) and the apex point C, is
called versed sine. It is also called mid‐ ordinate ( M).
• Right hand curve: If the curve deflects to the right of
the direction of the progress of survey.
• Left hand curve : If the curve deflects to the left of
the direction of the progress of survey.

18. Designation of curve
The sharpness of the curve is designated by two
ways.
(1) By radius (R)
(2) By Degree of Curvature (D)
By radius ( R)
Curve is known by the length of its radius‐ R

19. By Degree of Curvature (D)
Chord Definition Arc Definition
The Angle subtended at the
centre of curve by a chord of
30 or 20 mt. is called degree of
curvature.
The Angle subtended at
the centre of curve by an
arc of 30 or 20 mt. length
is called degree of curve.
If an angle subtended at
the centre of curve by a
chord of 20 mt is 5° , the
curve is called 5° curve
Used in America, canada,
India etc.

20. Relation between Degree and Radius of Curve
By Chord Definition
For a 30m chord, from triangle T1OM
Sin D/2 = T1M/OT1
= 15/R
Or R = 15/Sin D/2
Since D is very small, Sin D/2 = D/2
15
R = ________________
D/2 * π/180
R = 1719/D (for 30m chord)
R = 1146/D(for 20m chord)

21. Relation between Degree and Radius of Curve
By Arc Definition
If R is the radius of a curve and D is its degree for a 30m
arc, then
R * D * π/180 = 30
R = (30 * 180)/(D* π)
R = 1719/D
If D is the degree of a curve for a 20m arc, then
R * D * π/180 = 20
R = (20*180)/(D*π)
R = 1146/D

22. Formulae for elements of a simple Circular curve
Length of the curve
Let the length of the curve T1CT2 be l and let R be its radius.
Hence, l = RΔ
l = RΔ*π/180……where Δ is in degrees
If a 30m arc or chord definition is used, then
l= 1719 /D * Δ * π/180
= 30 Δ/D
If a 20m arc or chord definition is used, then
l= 1149 /D * Δ * π/180
= 20 Δ/D

23. Elements of Simple Circular Curve
14.5 20 20
5.5
20

24. Tangent Length
Tangent length, T = IT1 = IT2
= R * Tan(Δ/2)
Long Chord Length
Long Chord length = L = T1DT2
From Triangle OT1D
Sin(Δ/2) = T1D/R
T1D = R Sin(Δ/2)
Hence L = 2R Sin(Δ/2)

25. Apex Distance
Apex distance, IC = IO – CO
= R Sec(Δ/2) - R
= R(Sec(Δ/2) -1)
Mid ordinate
Mid ordinate Oo = CD = CO-DO
= R-R cos(Δ/2)
= R(1- cos(Δ/2))
= R vers Δ/2

26. A circular curve has a 200m radius and 65
degree deflection angle. What is its degree (a)
by arc definition and (b) chord definition. Also
calculate:
1) Length of the curve
2) Tangent Length
3) Length of long chord
4) Apex distance
5) Mid ordinate

27. Radius = 200m
Deflection angle = 65
Degree of Curve:
By Arc Definition:
Assuming a 30m arc length
R*D*π/180 = 30
200*D* π/180 = 30 = > D = 30*180/200 π = 8.595m
By Chord Definition:
Assuming a 30m chord length
R = 15/[D/2 * π/180 ] => D = 15*2*180/ π*200 = 8.595m
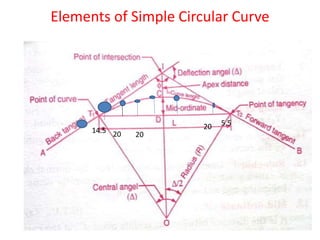
Length of the Curve = RΔ = 200*65* π/180 = 226.89m
Tangent Length = T = Rtan Δ/2 =200*tan(65/2)= 127.41m
Length of the long chord = L = 2Rsin Δ/2 = 2*200*sin(65/2) = 214.91m
Apex distance = R(sec (Δ/2) -1) = 200*(sec(65/2)-1) =37.13m
Mid-ordinate = R(1-cos Δ/2) = 200(1-cos(65/2)) = 31.32m

28. A circular curve has a 150m radius and 35 degree deflection angle. What is its degree
(a) by arc definition and (b) chord definition. Also calculate:
1) Length of the curve
2) Tangent Length
3) Length of long chord
4) Apex distance
5) Mid ordinate
Radius = 150m
Deflection angle = 35
Degree of Curve:
By Arc Definition:
Assuming a 30m arc length
R*D*π/180 = 30
150*D* π/180 = 30 = > D = 30*180/150π = 11.459m
By Chord Definition:
Assuming a 30m chord length
R = 15/[D/2 * π/180 ] => D = 15*2*180/ π*150 =11.459 m
Length of the Curve = RΔ = 150*35* π/180 = 91.629m
Tangent Length = T = Rtan Δ/2 =150*tan(35/2)= 47.29m
Length of the long chord = L = 2Rsin Δ/2 = 2*150*sin(35/2) = 90.21m
Apex distance = R(sec (Δ/2) -1) = 150*(sec(35/2)-1) =7.27m
Mid-ordinate = R(1-cos Δ/2) = 150(1-cos(35/2)) = 6.942m

29. Two straight lines T1I and T2I interest at chainage 375+12, the
angle of deflection being 110. Calculate the chainage of the
tangent points of a right handed circular curve of 400m radius
110
400
T1
T2
I
Chainage of I = 375 +12 = 375(chains) +12 (links)
Assume that length of chain is 20m
Deflection angle = 110
Radius = 400m
Tangent Length = RtanΔ/2 = 400tan(110/2) =571.25m
Length of the curve = RΔ*π/180 = 400*3.14*110/180=767.55
Chainage of Point of Curve(T1) = Chainage of I –Tangent Length
375*20+12*0.2 – 571.25
= 6931.15m
Chainage of Point of Tangency(T2) = Chainage of T1+Length of curve
= 6931.15+767.55
= 7698.70m
Chainage of PC = 346(chains) +2.78(links)
Chainage of PT = 384(chains)+4.67(links)

30. It is required to set out a curve of radius 100m with pegs at
approximately 10m centers. The deflection angle is 60.Draw up
the data necessary for pegging out the curve by each of the
following methods
1)Offsets from long chord
2) Offsets from tangent
R= 100
a b
30
30
Mid ordinate = R(1-cosΔ/2) = 100(1-cos30) = 13.39m
X = 10, 20 , 30
Ox = O0-x2/2R
O10 = 13.39 – 10*10/2*100 = 12.89m
O20 = 13.39 -20*20/2*100 = 11.39m
O30 = 13.39-30*30/2*100 =8.89m
O40 = 13.39-40*40/2*100 = 5.39m
O50 = 13.39-50*50/2*100= 0.89m

31. • Offsets from tangent
R – Sqrt(R2 –X2)
X=10: O10 = 100-SQRT(100*100-10*10) = 0.5M
X= 20 : O20 = 100-SQRT(100*100-20*20)=2.02M
X=30: O30 = 100-SQRT(100*100-30*30) =4.60M
X=40:O40 = 100-SQRT(100*100-40*40)=8.35M
X=50:O50 = 100-SQRT(100*100-50*50)= 13.39M

32. Field Procedure of Rankine’s Method
1. Locate P.C(T1), P.T(T2) and P.I(I)
2. Set up the theodolite exactly at T1 and make its temporary adjustments.
3. Set the Vernier A to zero and bisect the PI. Clamp the lower plate.
4. Release the upper plate and set the Vernier A to read ∆1. The line of
sight is thus directed along T1a.
5. Hold the zero of the tape at T1, take a distance C1(T1a) and swing the
tape with an arrow till it is bisected by the theodolite. This establishes
the first point aon the curve.
6. Set the second deflection angle ∆2 on the scale so that the line of sight is
set along T1b.
7. With the zero of the tape held at a and an arrow at the other
end(chord distance = ab), swing the tape about a, till the arrow is
bisected by the theodolite at b. This establishes the second point on the
curve.
8. Repeat the same steps till the last point on the curve is fixed

33. Two Theodolite Method
• This method is most convenient when the ground is undulating , rough not
suitable for linear measurements.
• In this method, two theodolites are used and thus linear measurements
are completely eliminated.(Most accurate method).
• It is based on the principle that the angle between the tangent and the
chord is equal to the angle subtended by the chord in the opposite
segment.
Therefore
Angle IT1a = 𝛿1 = Angle aT2T1
And
Angle IT1b = 𝛿2 = Angle bT2T1

34. Field Procedure of Two Theodolite method
1. Set up one theodolite at PC(T1) and the other at PT(T2).
2. Set the Vernier A of both the theodolites to zero.
3. Direct the theodolite at T1 towards I and the theodolite at T2
towards T1.
4. Set an angle 𝛿1 in both the theodolites so as to direct the line of
sights towards T1a, and T2a, thus the point a, the point of
intersection of the two line of sights is established on the curve.
5. Similarly, point b is established by setting 𝛿2 in both the
theodolites and bisecting the ranging rod at b.
6. Repeat the same steps, till last point on the curve is fixed.
7. This method is expensive and time consuming, but most accurate.
8. Various points are established independent of each other and thus
the error in establishing a point is not transferred to the
subsequent points.

35. COMPOUND CURVES
• A Compound curve is a combination of two or more simple circular
curves with different radii.
• Two centered compound curve has two circular arcs of different
radii that deviate in the same direction and join at a common
tangent point also known as point of compound curvature.
• T1I and T2I are two straights intersecting at I.
• T1DT2 is the compound curve of radii R1 and R2
• D is the point of compound curvature
• MN is the common tangent making
deflection angles Δ1, Δ2 at M and N
so that
Δ = Δ1 + Δ2

36. From triangle IMN
IM/Sin Δ2 = IN/ SinΔ1 = MN/Sin(180-( Δ1+ Δ2))
Hence,
IM = MN Sin Δ2/Sin(180-( Δ1+ Δ2)) or
IM = MN Sin Δ2/Sin Δ
Also,
IN = MN Sin Δ1/Sin Δ
Common Tangent MN:
MD = R1 Tan Δ1/2 DN = R2 Tan Δ2/2
MN = MD + DN
Or
MN = R1 Tan Δ1/2 + R2 Tan Δ2/2
Length of main tangents IT1 and IT2
IT1 = T1M + MI
= R1 Tan Δ1/2 + MN Sin Δ2/Sin Δ
IT2 = T2N + NI
= R2 Tan Δ2/2 + MN Sin Δ1/Sin Δ

37. TRANSITION CURVE
• A curve of varying radius is known as ‘transition curve’ The radius of such
curve varies from infinity to certain fixed value A transition curve is
provided on both ends of the circular curve
• The transition curve is also called as spiral or easement curve
OBJECTIVE OF PROVIDING TRANSITION CURVES
1. To accomplish gradually the transition from the tangent to the circular
curve, and from the circular curve to the tangent
2. To obtain a gradual increase of curvature from zero at the tangent point
to the specified quantity at the junction of the transition curve with the
circular curve
3. To provide the super elevation gradually from zero at the tangent point to
the specified amount on the circular curve
4. To avoid the overturning of the vehicle

38. REQUIREMENT OF IDEAL TRANSITION CURVES
• It should meet the original straight tangentially
• It should meet the circular curve tangentially
• Its radius at the junction with the circular curve should be the same as
that of the circular curve
• The rate of increase of curvature along the transition curve should be
same as that of in increase of super elevation
• The length should be such that the full super elevation is attained at the
junction with the circular curve
The types of transition curve which are in common use are
• Cubic parabola
• A clothoid or spiral
• A lemniscate

39. SUPERELEVATION
When a vehicle passes from a straight path to curved one, the forces acting
on it are
i.The weight of the vehicle
ii.The centrifugal force both acting through the CG of vehicle
Since the centrifugal force is always acts in the direction perpendicular to the
axis of rotation which is vertical, its direction is always horizontal. The effect
of the centrifugal force is to push the vehicle off the track or rail. In order to
counteract the action, the plane of rails or the road surface is made
perpendicular to the resultant of centrifugal force and weight of the vehicle.
In other word, the outer rail is super elevated or raised above the inner one
Similarly the road should be “ i e the outer edge of the road should be raised
above the inner one, the raising of the outer rail or outer edge above the
inner one, being called as super elevation or cant
The amount of cant is depend on vehicle and radius of curve

40. Let,
W = weight of the vehicle
P = the centrifugal force
v = the speed of the vehicle in m/s
g = =the acceleration due to gravity 9 81 m/s 2
R = the radius of the curve in m
h = the super elevation in m
B = Width of pavement(m)
Θ = angle of super elevation
For equilibrium, the resultant R of these two forces
should be perpendicular to the road surface
Tan θ = P/W also, Tan θ = h/B
Hence, h/B = P/W =
ℎ = 𝐵𝑣2/𝑔𝑅 for highways ℎ = 𝐺𝑣2/𝑔𝑅 for railways , where G is the gauge of track
The amount of super elevation is limited about 1/12 th of the gauge, 1/10 th
being permitted under special circumstances

41. Centrifugal Ratio:
The ratio of the centrifugal force and the weight is called centrifugal ratio.
Centrifugal ratio = P/W = v2/gR
The maximum value of centrifugal ratio is taken as equal to ¼ for roads and 1/8
for railways
For roads, P/W = 1/4 = V2/gR  V = Sqrt(gR/4)
For railways, P/W = 1/8 = V2/gR  v = Sqrt(gR/8)
For a given radius , the speed on a highway can be higher than on railways by √2
times.
Hands off Velocity
For stability, v = Sqrt(gRtanθ )
If a vehicle moves with a velocity v on a curve of radius R with super elevation θ ,
the vehicle steers itself along the curve without the driver using the steering
wheel. Such a velocity is known as hands off velocity.

42. Length of Transition Curves
The length of transition curve should be such that full super
elevation is attained at the end of transition curve applied at a
suitable rate.
By rate of super elevation method
If the rate of application of super elevation is 1 in n of the length
of the curve and h is the super elevation, the length of the
transition curve is given by
L = nh
Where h = Gv2/gR (metres)
The value of n may vary between 300 and 1200

43. By time rate
• Let the time rate of application of super elevation be x cm/s,
length of transition curve be L metre, super elevation be h cm,
and speed of the vehicle be v m/s
• As x cm cant is applied in 1 second, full cant of h cm will be
applied in h/x seconds ( = t seconds)
• Distance travelled = speed * time
= v * t
L = v* h/x
L = Gv3/xgR (metres)

44. By rate of change of radial acceleration
• This rate should be such that the passenger should not
experience any sensation of discomfort when the train
travelling over the curve. It is taken as 30 cm per sec 3.
• Length of the transition curve is given by
L = v3/0.3R ( v is in m/s)
L = V3/14R ( V is in kmph)
If centrifugal ratio is given and comfort condition holds good
L = 4.5 √R ……..For railways
L = 12.8√R……. For roadways

45. Reverse Curve
• A reverse or serpentine curve is defined as a compound curve
having two circular arcs of same or different radii, but curving in
opposite directions with a common tangent.(Point of reverse
curvature)
Uses
• Reverse curves are adopted where the straights are parallel or
when their angle of intersection is too acute.
• Frequently used for railway sidings
• Adopted for roads and railways designed for slow speeds
• They are unavoidable in valley regions
They should be avoided in highways and railways designed for high
speeds due to following reasons:
Sudden change of super elevation is needed from one edge to the
other one , near the point of reverse curvature
Sudden change of curvature and direction reduces the life of vehicle
and gives discomfort to passengers
It is not possible to provide proper super elevation at point of reverse
curvature
It is therefore suggested to provide a straight length or a reversed
transition curve between two branches of reverse curve.

46. Elements of Reverse Curve
Non – Parallel Straights Parallel Straights

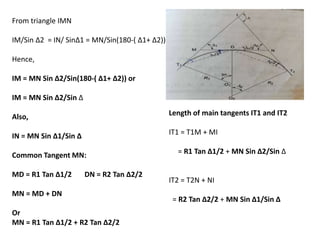
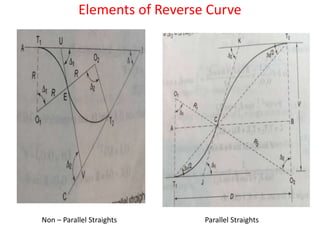
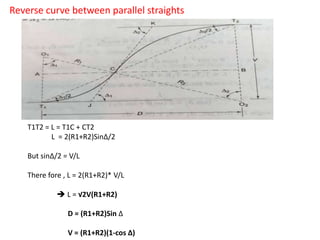
47. Reverse curve between non-straights
Given angles Δ1 & Δ2, length of common tangent (Δ2 > Δ1)- to find out common radius R
and chainage of T1,E and T2
R = d/[tan Δ1/2 + tan Δ2/2] , Chainage of T1 = Chainage of I – IT1
Chainage of E = Chainage of T1 + Length of first arc(𝜋RΔ1/180)
Chainage of T2 = Chainage of E + length of second arc(𝜋RΔ2/180)

48. Reverse curve between parallel straights
T1T2 = L = T1C + CT2
L = 2(R1+R2)SinΔ/2
But sinΔ/2 = V/L
There fore , L = 2(R1+R2)* V/L
 L = √2V(R1+R2)
D = (R1+R2)Sin Δ
V = (R1+R2)(1-cos Δ)

49. Vertical Curves
• A curve used to connect two different grade lines of railways
or highways is called a vertical curve.
• These are provided to avoid an abrupt change in rate of grade
and provide safe and comfortable journey.
• Absence of vertical curves causes sudden impact or jerk to
vehicles which may be dangerous.
• A vertical curve may be circular or parabolic, preferably
parabolic due to following reasons:
• It is flatter at top and hence provides a longer sight distance,
greater the sight distance, lesser is the possibility of any
accident.
• Rate of change of grade is uniform through out and hence
produces best riding qualities
• Simple in computation works.

50. The general equation of a parabolic curve with a vertical axis is
given by
Y = ax2 +bx+c
The slope of the this curve at any point is given by
dy/dx = 2ax + b
The rate of change of slope or rate of change of grade is given by
d2y/ dx2 = 2a = constant
Thus, for a parabola with a vertical axis, the rate of change of
grade is uniform and it ensures a comfortable safe ride

51. Grade:
The grade or gradient of a road/rail can be expressed either in
percentage or ratio
Rate of change of gradient
The rate of the algebraic difference of two gradients meeting
at the apex of a curve to the length of curve is known as rate
of change of gradient.
r = (g1-g2)/L
r=rate of change of gradient, L = Length of curve, g1,g2 =
grades
For first class railways, r is 0.10% per 30m pegs in summit
curves and 0.05% per 30m pegs in sag curves+

52. Types of vertical curves
Summit Curve or Convex curve
This is provided in either of the following three cases:
• When an upgrade is followed by a downgrade
• When a steeper upgrade is followed by a milder upgrade
• When a milder downgrade is followed by a steeper
downgrade

53. Sag Curve or Concave curve or valley curve
• When a downgrade is followed by an upgrade
• When a steeper downgrade is followed by a milder
downgrade
• When a milder upgrade is followed by steeper upgrade

54. Length of vertical curve
Length of the curve = Total change of grade/Permissible rate of
change of grade
For example, If two grades of +1.2% and -0.9% meet, the length
of the curve required for a rate of change of grade of 0.1% per
30m chain will be
L = [1.2-(-0.9)/0.1] * 30 = 630m
Length of a vertical curve should always be an even number of
chains so that half of its can be provided on either side of the
apex.

55. Sight Distance
For safe movement of vehicles on roads, the aspect of visibility play an
important role.
The driver of the vehicle should be able to see clearly at least a certain
portion of road length to avoid collision or accident.
The absolute minimum length of the road required for this purpose is
known as stopping sight distance or non-passing sight distance
As per IRC, SSD is defined as the length of highway required to bring
a vehicle to a stop at various design speeds when the eye of the drive
is 120cm above the pavement and the object causing the stop is
15cm above pavement.
SSD is dependent on efficiency of brakes, frictional resistance between
road and tyres, slope of road, speed of vehicle and reaction time of
driver

56. Sight distance (S) less than the length of the
curve
L = NS2/800h , Where N= g1-g2
Sight distance(S) greater than length of curve(L)
L = 2S – [200(√h1+ √h2)2]/(g1-g2)