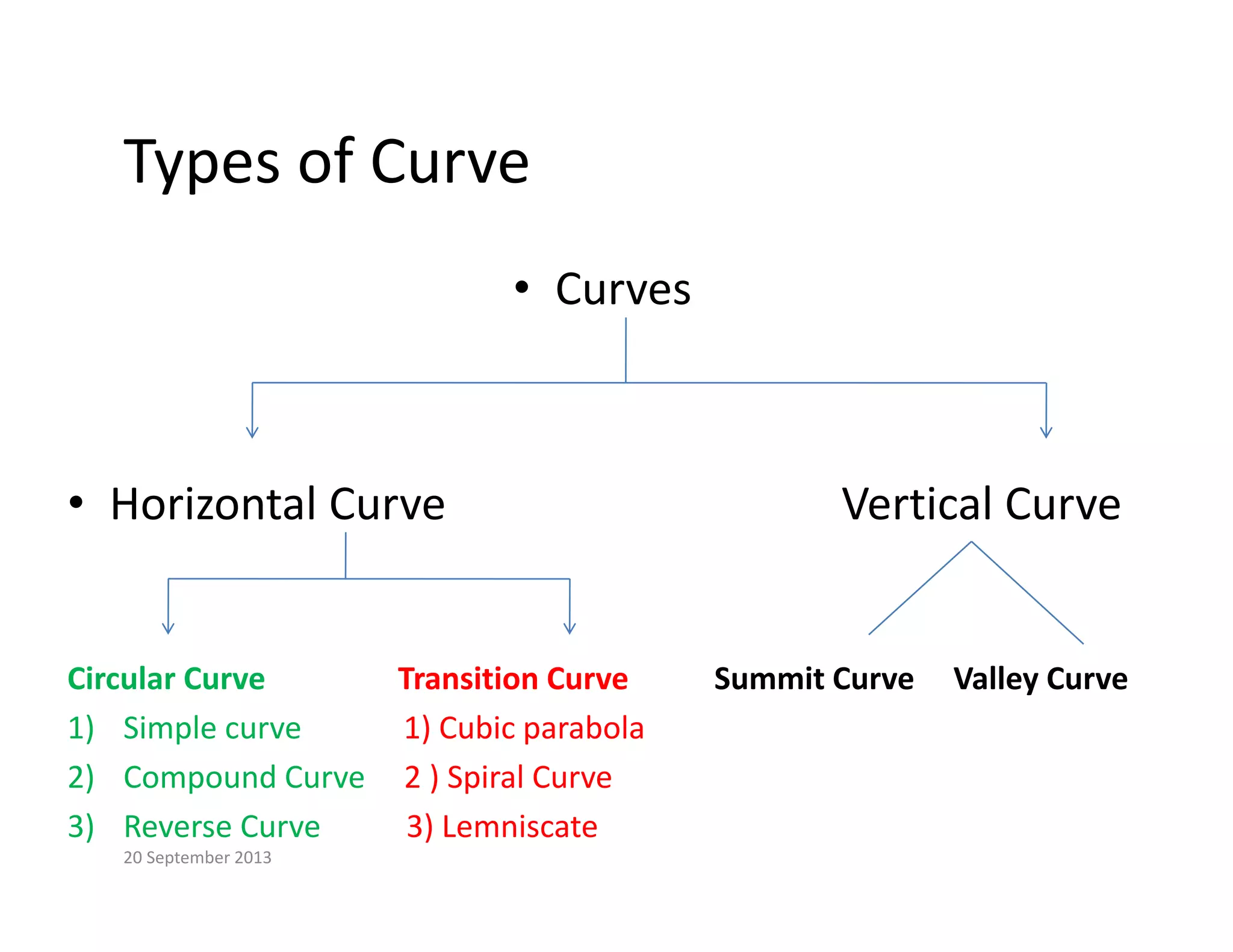
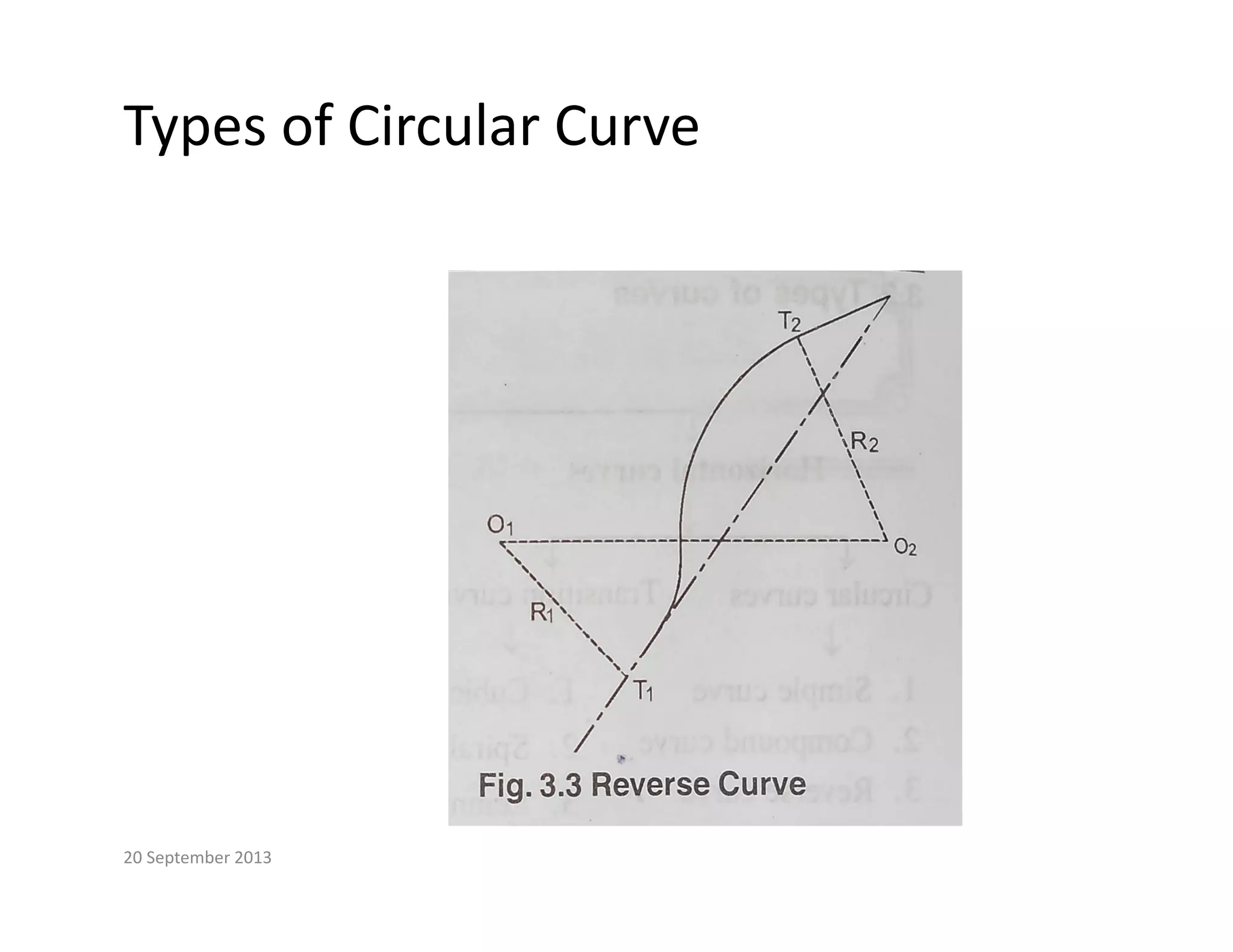
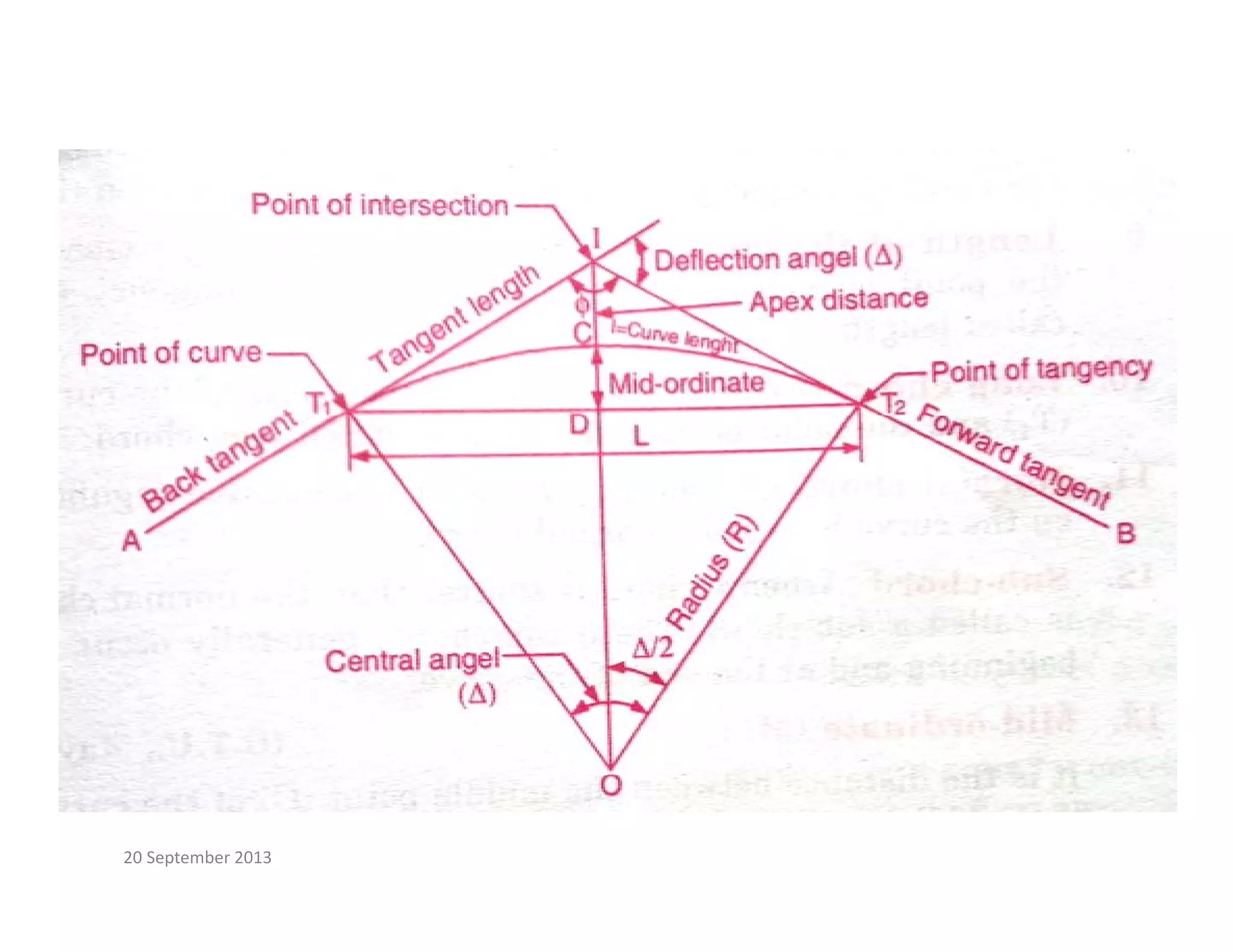
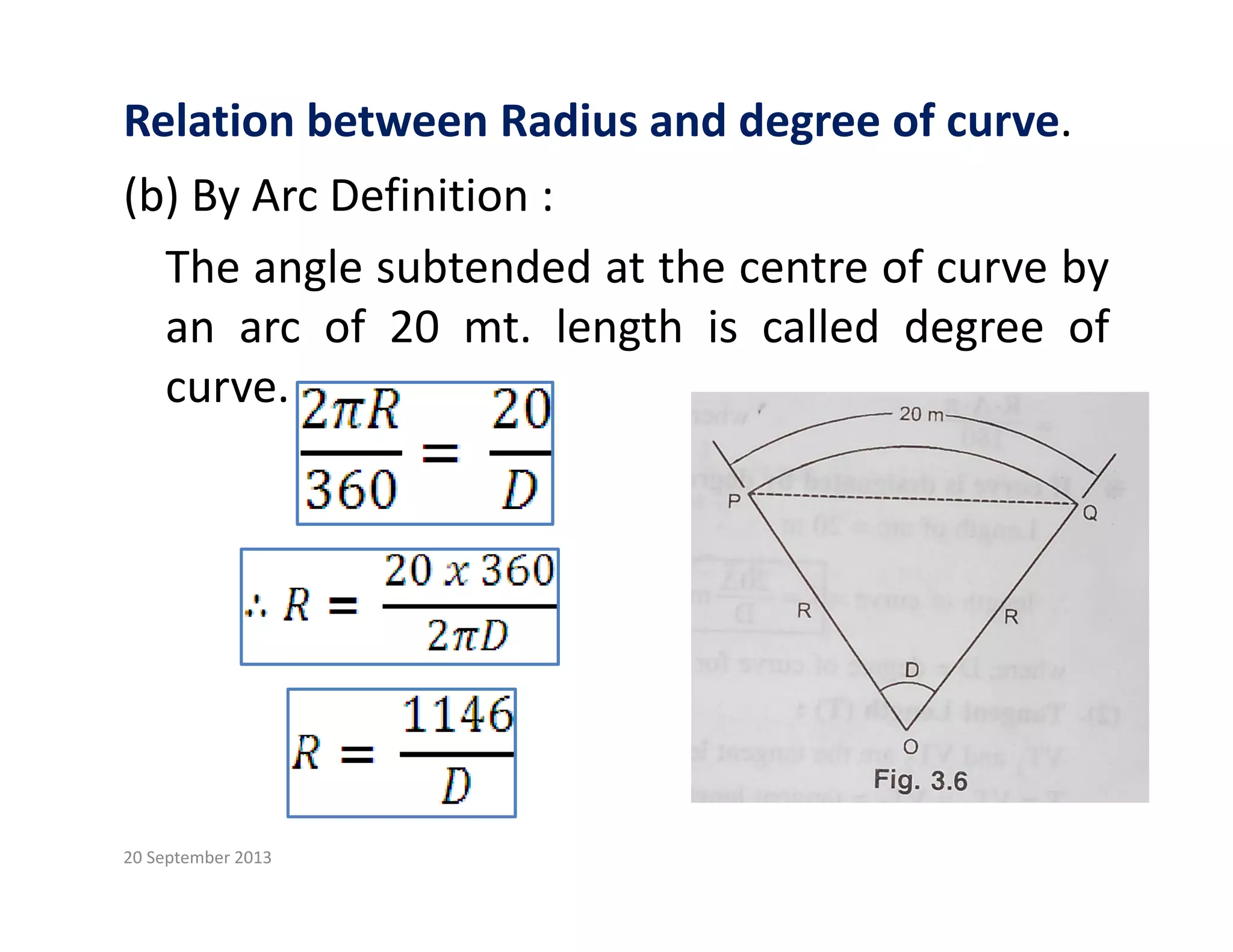
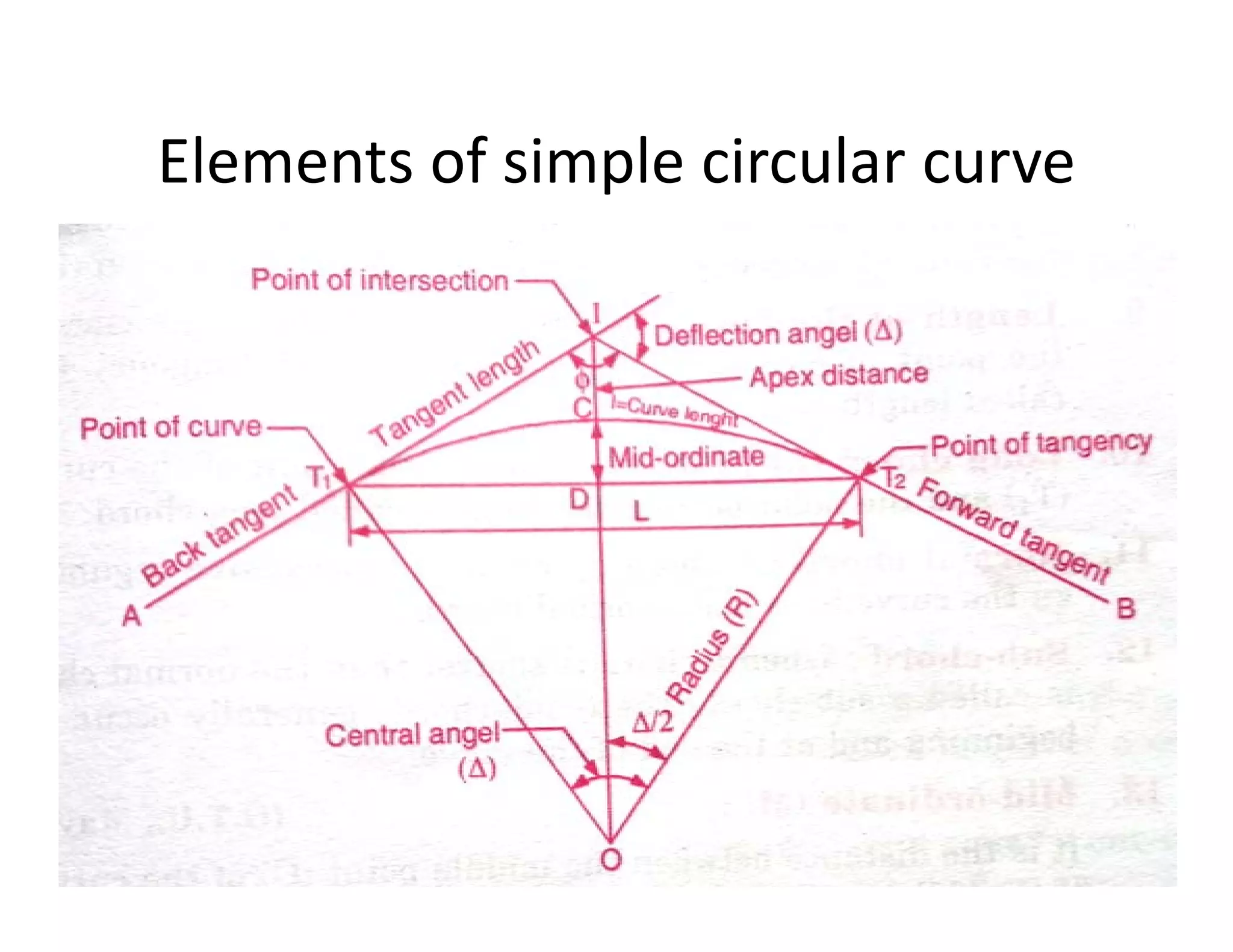
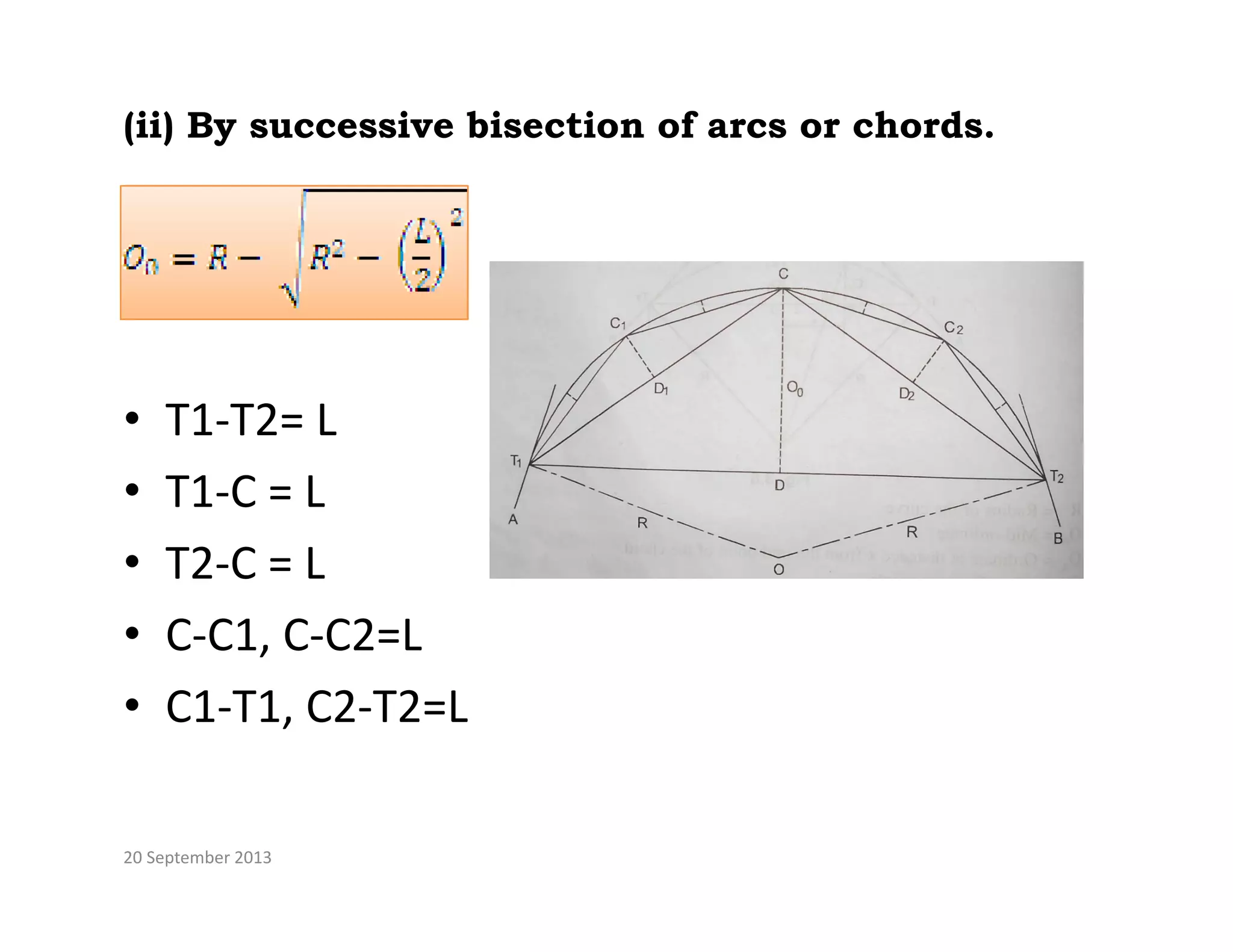
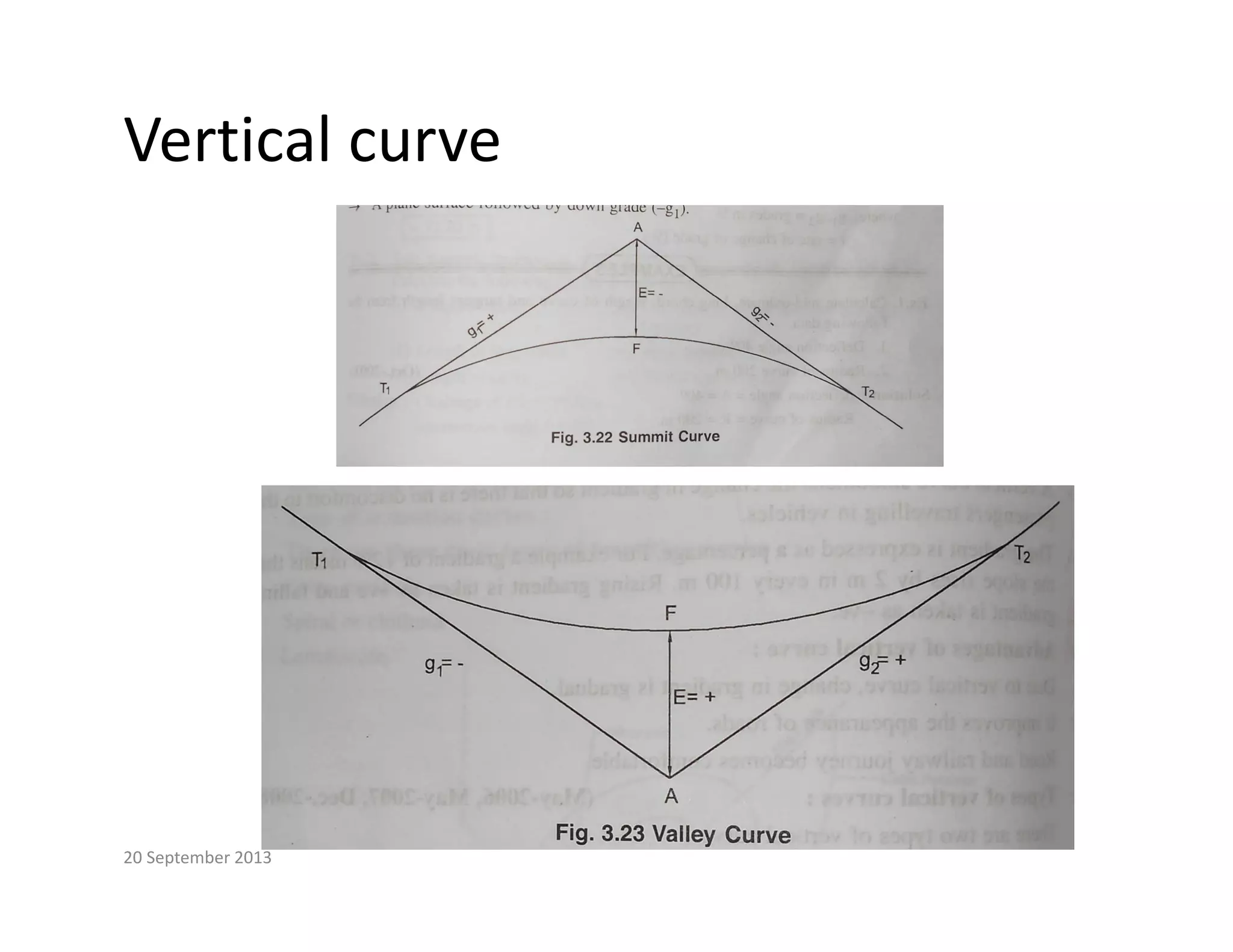
This document provides an overview of circular curves used in surveying and transportation design. It begins with 10 questions asked about curves in previous GTU exams, covering topics like setting out circular curves using different methods, elements of compound and reverse curves, transition curves, and types of vertical curves. The document then outlines the lecture, discussing why curves are used and different types of horizontal and vertical curves. It explains the components, properties, and setting out of simple circular curves, including definition of terms like radius, deflection angle, and chord length. It also covers methods for setting out a circular curve, both linear and angular methods.