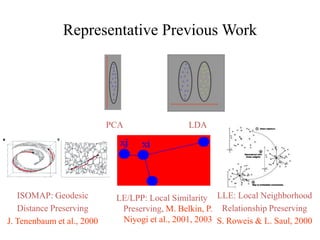
This document discusses dimensionality reduction algorithms and proposes a unified framework. It summarizes previous algorithms like PCA, LDA, ISOMAP and describes how they can be viewed as special cases of a general formulation involving intrinsic and penalty graphs. A new algorithm, Marginal Fisher Analysis, is introduced that utilizes label and local manifold structure information for tasks like face recognition. Experimental results demonstrate its effectiveness. The document also outlines future work on machine learning, event recognition, biometrics and multimedia content analysis.

1. Representative Previous WorkPCALDAISOMAP: Geodesic Distance PreservingJ. Tenenbaum et al., 2000LLE: Local Neighborhood Relationship PreservingS. Roweis & L. Saul, 2000LE/LPP: Local Similarity Preserving, M. Belkin, P. Niyogi et al., 2001, 2003

2. HundredsDimensionality Reduction AlgorithmsStatistics-basedGeometry-based…PCA/KPCAISOMAPLLELE/LPP…LDA/KDAMatrixTensorAny common perspective to understand and explain these dimensionality reduction algorithms? Or any unified formulation that is shared by them?Any general tool to guide developing new algorithms for dimensionality reduction?

3. Our AnswersDirect Graph EmbeddingLinearizationKernelizationOriginal PCA & LDA,ISOMAP, LLE,Laplacian EigenmapPCA, LDA, LPPKPCA, KDATensorizationTypeFormulationCSA, DATERExampleS. Yan, D. Xu, H. Zhang and et al., CVPR, 2005, T-PAMI,2007

4. Direct Graph EmbeddingIntrinsic Graph:S, SP: Similarity matrix (graph edge)Similarity in high dimensional spaceL, B:Laplacian matrix from S, SP;Data in high-dimensional space and low-dimensional space (assumed as 1D space here):Penalty Graph

5. Direct Graph Embedding -- ContinuedIntrinsic Graph:S, SP: Similarity matrix (graph edge)L, B:Laplacian matrix from S, SP;Similarity in high dimensional spaceData in high-dimensional space and low-dimensional space (assumed as 1D space here):Criterion to Preserve Graph Similarity:Penalty Graph Special case B isIdentity matrix (Scale normalization)Problem: It cannot handle new test data.

6. LinearizationIntrinsic GraphLinear mapping functionPenalty GraphObjective function in LinearizationProblem: linear mapping function is not enough to preserve the real nonlinear structure?

7. KernelizationIntrinsic GraphNonlinear mapping:the original input space to anotherhigher dimensional Hilbert space.Penalty GraphConstraint:Kernel matrix:Objective function in Kernelization

8. Tensorization Low dimensional representation is obtained as:Intrinsic GraphPenalty GraphObjective function in Tensorizationwhere

9. Common FormulationS, SP: Similarity matrixIntrinsic graphL, B:Laplacian matrix from S, SP;Penalty graphDirect Graph EmbeddingLinearizationKernelizationTensorizationwhere

10. A General Framework for Dimensionality ReductionD: Direct Graph Embedding L:LinearizationK: KernelizationT: Tensorization

11. New Dimensionality Reduction Algorithm: Marginal Fisher AnalysisImportant Information for face recognition:1) Label information 2) Local manifold structure (neighborhood or margin) 1: ifxi is among the k1-nearest neighbors of xj in the same class;0 :otherwise1: if the pair (i,j) is among the k2 shortest pairs among the data set;0: otherwise

12. Marginal Fisher Analysis: AdvantageNo Gaussian distribution assumption

13. Experiments: Face Recognition

14. SummaryOptimization framework that unifies previous dimensionality reduction algorithms as special cases.A new dimensionality reduction algorithm: Marginal Fisher Analysis.

15. Event Recognition in News VideoOnline and offline video search

16. 56 events are defined in LSCOMAirplane FlyingRiotExisting CarGeometric and photometric variancesClutter backgroundComplex camera motion and object motionMore diverse !

17. Earth Mover’s Distance in Temporal Domain(T-MM, Under Review)Key Frames of two video clips in class “riot”EMD can efficiently utilize the information from multiple frames.

18. Multi-level Pyramid Matching (CVPR 2007, Under Review)One Clip = several subclips (stages of event evolution) .No prior knowledge about the number of stages in an event, and videos of the same event may include a subset of stage only. SmokeLevel-1FireLevel-1Level-0Level-0FireLevel-1SmokeLevel-1Solution: Multi-level Pyramid Matching in Temporal Domain

19. Other Publications & Professional ActivitiesOther Publications: Kernel based Learning:Coupled Kernel-based Subspace Analysis: CVPR 2005 Fisher+Kernel Criterion for Discriminant Analysis: CVPR 2005Manifold Learning:Nonlinear Discriminant Analysis on Embedding Manifold : T-CSVT (Accepted)Face Verification:Face Verification with Balanced Thresholds: T-IP (Accepted)Multimedia:Insignificant Shadow Detection for Video Segmentation: T-CSVT 2005Anchorperson extraction for Picture in Picture News Video: PRL 2005Guest Editor: Special issue on Video Analysis, Computer Vision and Image Understanding

20. Special issue on Video-based Object and Event Analysis, Pattern RecognitionLettersBook Editor:Semantic Mining Technologies for Multimedia DatabasesPublisher: Idea Group Inc. (www.idea-group.com)

21. Future WorkMachine LearningEvent RecognitionBiometricComputer VisionPattern RecognitionWeb SearchMultimedia ContentAnalysisMultimedia

22. AcknowledgementShuicheng Yan UIUCSteve Lin MicrosoftLei Zhang MicrosoftHong-Jiang ZhangMicrosoftShih-Fu ChangColumbiaXuelong Li UKXiaoou TangHong KongZhengkai Liu, USTC

23. Thank You very much!

24. What is Gabor Features?Gabor features can improve recognition performance in comparison to grayscale features. Chengjun Liu T-IP, 2002Five Scales…Input: GrayscaleImageEight OrientationsOutput: 40 Gabor-filteredImagesGabor Wavelet Kernels

25. How to Utilize More Correlations?Pixel RearrangementPixelRearrangementSets of highlycorrelated pixelsColumns of highlycorrelated pixelsPotential Assumption in Previous Tensor-based Subspace Learning:Intra-tensor correlations: Correlations among the features within certain tensor dimensions, such as rows, columns and Gabor features…