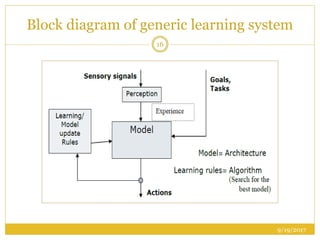
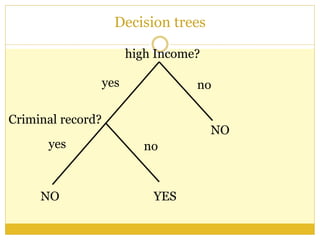
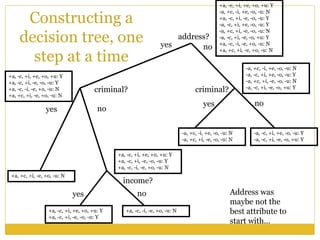
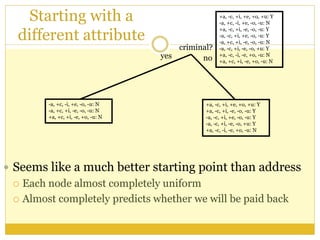
The document outlines foundational concepts of artificial intelligence (AI) and machine learning (ML), emphasizing the importance of learning from experience in AI applications. It distinguishes between deductive and inductive reasoning, explaining various learning types such as supervised, unsupervised, active, and reinforcement learning. Additionally, it discusses the critical role of machine learning in overcoming knowledge acquisition challenges and the significance of decision trees in making predictions based on learned data.

1. PROF.MRS.M.P.ATRE
ASSISTANT PROFESSOR,
PVGCOET
Learning
9/19/2017
1

2. AI : first 3 units
9/19/2017
2
 Foundation
 Searching
 Knowledge Representation

3. Why is learning important?
 So far we have assumed we know how the
world works
 Rules of queens puzzle
 Rules of chess
 Knowledge base of logical facts
 Actions’ preconditions and effects
 Probabilities in Bayesian networks

4. 9/19/2017
4
 At that point “just” need to solve/optimize
 In the real world this information is often not
immediately available
 AI needs to be able to learn from experience

5. What is learning
 Machine Learning is the study of how to build
computer systems that adapt and improve with
experience
 subfield of Artificial Intelligence
 intersects with
 cognitive science,
 information theory,
 and probability theory, among others
9/19/2017
5

6. Reasoning and Learning
9/19/2017
6
 AI deals mainly with deductive reasoning
 Deductive reasoning arrives at answers to queries
relating to a particular situation starting from a set of
general axioms
 Learning represents inductive reasoning
 inductive reasoning arrives at general axioms from a
set of particular instances

7. Deductive Vs Inductive
9/19/2017
7
 Deductive Reasoning (teacher explains, give
examples and then students practice)
 Generalization(or Rule) Specific Examples or Activities
 Inductive Reasoning (teacher presents students
with many examples showing how the concept is
used to make students “NOTICE”)
 Specific Examples or ActivitiesGenralization(or Rule)

8. Classical AI
9/19/2017
8
 suffers from the knowledge acquisition problem in
real life applications
 obtaining and updating the knowledge base is costly
and prone to errors
 So the need for Machine Learning

9. Machine learning serves to solve
the knowledge acquisition
bottleneck by obtaining the
result from data by induction
9/19/2017
9

10. Machine learning is particularly attractive
because
9/19/2017
10
 Some tasks cannot be defined well except by
example
 Working environment of machines may not
be known at design time
 Explicit knowledge encoding may be difficult
and not available
 Environments change over time
 Biological systems learn

11. Wide applications where learning used
9/19/2017
11
 Data mining and knowledge discovery
 Speech/image/video (pattern) recognition
 Adaptive control
 Autonomous vehicles/robots
 Decision support systems
 Bioinformatics
 WWW
 ( Data mining is the practice of examining the large pre-
existing databases in order to generate new information)

12. Defining Learning
9/19/2017
12
 Formally, a computer program is said to learn from
experience E with respect to some class of
tasks T and performance measure P,
 if its performance at tasks in T, as measured
by P, improves with experience E

13. Thus a learning system is characterized by:
9/19/2017
13
 • task T
 • experience E, and
 • performance measure P

14. Example 1
9/19/2017
14
 Learning to play chess
 T: Play chess
 P: Percentage of games won in world tournament
 E: Opportunity to play against self or other players

15. Example 2
9/19/2017
15
 Learning to drive a van
 T: Drive on a public highway using vision sensors
 P: Average distance traveled before an error
(according to human observer)
 E: Sequence of images and steering actions recorded
during human driving.

16. Block diagram of generic learning system
9/19/2017
16

17. So learning system consists of
9/19/2017
17
 Goal: Defined with respect to the task to be
performed by the system
 Model: A mathematical function which maps
perception to actions
 Learning rules: Which update the model
parameters with new experience such that the
performance measures with respect to the goals is
optimized
 Experience: A set of perception (and possibly the
corresponding actions)

18. Taxonomy of Learning Systems
9/19/2017
18
 Or Classification based on above block diagram

19. 1. Goal/Task/Target Function:
9/19/2017
19
 Prediction: To predict the desired output for a
given input based on previous input/output pairs.
 E.g., to predict the value of a stock given other
inputs like market index, interest rates etc.
 Categorization: To classify an object into one of
several categories based on features of the object.
 E.g., a robotic vision system to categorize a machine
part into one of the categories, spanner, hammer etc
based on the parts’ dimension and shape.

20. 9/19/2017
20
 Clustering: To organize a group of objects into
homogeneous segments. E.g., a satellite image
analysis system which groups land areas into
forest, urban and water body, for better utilization
of natural resources.
 Planning: To generate an optimal sequence of
actions to solve a particular problem. E.g., an
Unmanned Air Vehicle which plans its path to
obtain a set of pictures and avoid enemy anti-
aircraft guns.

21. 2.Models
9/19/2017
21
 • Propositional and FOL rules
 • Decision trees
 • Linear separators
 • Neural networks
 • Graphical models
 • Temporal models like hidden Markov models

22. 3.Learning Rules
9/19/2017
22
 often tied up with the model of learning used
 Some common rules :
 gradient descent,
 least square error,
 expectation maximization
 and margin maximization

23. 4. Experiences
9/19/2017
23
 Learning algorithms use experiences in the form of
perceptions or perception action pairs to
improve their performance
 nature of experiences varies with applications
 Supervised learning
 UnSupervised learning
 Active learning
 Reinforcement learning

24. 4.1 Supervised learning:
9/19/2017
24
 A teacher or oracle is available
 It provides the desired action corresponding to a
perception
 A set of perception action pair provides a training set
 Examples :
 an automated vehicle where a set of vision inputs and the
corresponding steering actions are available to the learner

25. 4.2 Unsupervised learning:
9/19/2017
25
 no teacher is available
 learner only discovers persistent patterns in the data
consisting of a collection of perceptions
 also called exploratory learning
 Examples:
 Finding out malicious network attacks from a sequence of
anomalous data packets is an example of unsupervised
learning

26. 4.3 Active learning:
9/19/2017
26
 not only a teacher is available,
 the learner has the freedom to ask the teacher for
suitable perception-action example pairs which will
help the learner to improve its performance
 Examples:
 a news recommender system which tries to learn user’s
preferences and categorize news articles as interesting or
uninteresting to the user.
 The system may present a particular article (of which it is not
sure) to the user and ask whether it is interesting or not.

27. 4.4 Reinforcement learning:
9/19/2017
27
 a teacher is available,
 but the teacher instead of directly providing the
desired action corresponding to a perception,
return reward and punishment to the learner
for its action corresponding to a perception
 Examples:
 a robot in a unknown terrain where its get a punishment when
its hits an obstacle and reward when it moves smoothly

28. Mathematical formulation of the inductive
learning problem
9/19/2017
28
 Extrapolate from a given set of examples so that we
can make accurate predictions about future
examples.
 Supervised versus Unsupervised learning
 Want to learn an unknown function f(x) = y, where x
is an input example and y is the desired output.
 Supervised learning implies we are given a set of (x,
y) pairs by a "teacher."
 Unsupervised learning means we are only given the
x s. In either case, the goal is to estimate f.

29. Inductive Bias
9/19/2017
29
 Inductive learning - inherently conjectural process
because any knowledge created by generalization
from specific facts cannot be proven true; it can only
be proven false.
 Hence, inductive inference is falsity preserving,
not truth preserving

30. 9/19/2017
30
 To generalize beyond the specific training examples,
we need constraints or biases on what f is best.
 That is, learning can be viewed as searching
the Hypothesis Space H of possible f
functions

31. 9/19/2017
31
 A bias allows us to choose one f over another one
 A completely unbiased inductive algorithm could
only memorize the training examples and could not
say anything more about other unseen examples

32. Two types of biases commonly used ML
9/19/2017
32
 Machine Learning : Types of Biases
 Restricted Hypothesis Space Bias
 Allow only certain types of f functions, not arbitrary ones
 Preference Bias
 Define a metric for comparing fs so as to determine
whether one is better than another

33. Inductive Learning Framework
9/19/2017
33

34. 9/19/2017
34
Example

35. 9/19/2017
35
 We lend money to people
 We have to predict whether they will pay us back or not
 People have various (say, binary) features:
 do we know their Address?
 do they have a Criminal record?
 high Income?
 Educated?
 Old?
 Unemployed?

36. 9/19/2017
36
 We see examples: (Y = paid back, N = not)
+a, -c, +i, +e, +o, +u: Y
-a, +c, -i, +e, -o, -u: N
+a, -c, +i, -e, -o, -u: Y
-a, -c, +i, +e, -o, -u: Y
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, -e, -o, +u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N
 Next person is +a, -c, +i, -e, +o, -u. Will we
get paid back?

37. 9/19/2017
37
 We want some hypothesis h that predicts whether we will
be paid back
+a, -c, +i, +e, +o, +u: Y
-a, +c, -i, +e, -o, -u: N
+a, -c, +i, -e, -o, -u: Y
-a, -c, +i, +e, -o, -u: Y
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, -e, -o, +u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N

38. 9/19/2017
38
 Lots of possible hypotheses: will be paid back if…
 Income is high (wrong on 2 occasions in training data)
 Income is high and no Criminal record (always right in
training data)
 (Address is known AND ((NOT Old) OR Unemployed))
OR ((NOT Address is known) AND (NOT Criminal
Record)) (always right in training data)
 Which one seems best? Anything better?

39. Occam’s Razor
9/19/2017
39
 Occam’s razor: simpler hypotheses tend to
generalize to future data better
 Intuition: given limited training data,
 it is likely that there is some complicated hypothesis that is not
actually good but that happens to perform well on the training
data
 it is less likely that there is a simple hypothesis that is not
actually good but that happens to perform well on the training
data
 There are fewer simple hypotheses
 Computational learning theory studies this in much
more depth

40. Occam’s Razor : a problem-solving principle
9/19/2017
40
 Occam’s Razor/ Ockham’s razor is a principle from
philosophy
 Suppose there exist two explanations for an
occurrence
 In this case, the simpler one is usually better
 Another way of saying it is that the more
assumptions you have to make, the more unlikely the
explanation is!

41. Decision trees
high Income?
yes no
NO
yes no
NO
Criminal record?
YES

42. Constructing a
decision tree, one
step at a time
address?
yes no
+a, -c, +i, +e, +o, +u: Y
-a, +c, -i, +e, -o, -u: N
+a, -c, +i, -e, -o, -u: Y
-a, -c, +i, +e, -o, -u: Y
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, -e, -o, +u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N
-a, +c, -i, +e, -o, -u: N
-a, -c, +i, +e, -o, -u: Y
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, -e, -o, +u: Y
+a, -c, +i, +e, +o, +u: Y
+a, -c, +i, -e, -o, -u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N
criminal? criminal?
-a, +c, -i, +e, -o, -u: N
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, +e, -o, -u: Y
-a, -c, +i, -e, -o, +u: Y
+a, -c, +i, +e, +o, +u: Y
+a, -c, +i, -e, -o, -u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N
income?
+a, -c, +i, +e, +o, +u: Y
+a, -c, +i, -e, -o, -u: Y
+a, -c, -i, -e, +o, -u: N
yes no
yes no
yes no Address was
maybe not the
best attribute to
start with…

43. Starting with a
different attribute
yes no
+a, -c, +i, +e, +o, +u: Y
-a, +c, -i, +e, -o, -u: N
+a, -c, +i, -e, -o, -u: Y
-a, -c, +i, +e, -o, -u: Y
-a, +c, +i, -e, -o, -u: N
-a, -c, +i, -e, -o, +u: Y
+a, -c, -i, -e, +o, -u: N
+a, +c, +i, -e, +o, -u: N
criminal?
-a, +c, -i, +e, -o, -u: N
-a, +c, +i, -e, -o, -u: N
+a, +c, +i, -e, +o, -u: N
+a, -c, +i, +e, +o, +u: Y
+a, -c, +i, -e, -o, -u: Y
-a, -c, +i, +e, -o, -u: Y
-a, -c, +i, -e, -o, +u: Y
+a, -c, -i, -e, +o, -u: N
 Seems like a much better starting point than address
 Each node almost completely uniform
 Almost completely predicts whether we will be paid back

44. Hypothesis Spaces
9/19/2017
44
 How many distinct decision trees are there with ‘n’
Boolean attributes?
 =number of Boolean functions
 Number of distinct truth tables with (2^n) rows
 2^(2^n) distinct decision trees
 E.g with 6 Boolean attributes, there are
18,446,744,073,709,551,616 trees

45. Different approach: nearest neighbor(s)
 Next person is -a, +c, -i, +e, -o, +u. Will we get paid
back?
 Nearest neighbor: simply look at most similar example
in the training data, see what happened there
+a, -c, +i, +e, +o, +u: Y (distance 4)
-a, +c, -i, +e, -o, -u: N (distance 1)
+a, -c, +i, -e, -o, -u: Y (distance 5)
-a, -c, +i, +e, -o, -u: Y (distance 3)
-a, +c, +i, -e, -o, -u: N (distance 3)
-a, -c, +i, -e, -o, +u: Y (distance 3)
+a, -c, -i, -e, +o, -u: N (distance 5)
+a, +c, +i, -e, +o, -u: N (distance 5)

46. 9/19/2017
46
 Nearest neighbor is second, so predict N
 k nearest neighbors: look at k nearest neighbors,
take a vote
 E.g., 5 nearest neighbors have 3 Ys, 2Ns, so predict Y
These nearest neighbours are
+a, -c, +i, +e, +o, +u: Y (distance 4)
-a, +c, -i, +e, -o, -u: N (distance 1)
-a, -c, +i, +e, -o, -u: Y (distance 3)
-a, +c, +i, -e, -o, -u: N (distance 3)
-a, -c, +i, -e, -o, +u: Y (distance 3)

47. Another approach: perceptrons
 Place a weight on every attribute, indicating how
important that attribute is (and in which direction it
affects things)
 E.g., wa = 1, wc = -5, wi = 4, we = 1, wo = 0, wu = -1
+a, -c, +i, +e, +o, +u: Y (score 1+4+1+0-1 = 5)
-a, +c, -i, +e, -o, -u: N (score -5+1=-4)
+a, -c, +i, -e, -o, -u: Y (score 1+4=5)
-a, -c, +i, +e, -o, -u: Y (score 4+1=5)
-a, +c, +i, -e, -o, -u: N (score -5+4=-1)
-a, -c, +i, -e, -o, +u: Y (score 4-1=3)
+a, -c, -i, -e, +o, -u: N (score 1+0=1)
+a, +c, +i, -e, +o, -u: N (score 1-5+4+0=0)

48. How to calculate the score?
9/19/2017
48
 wa = 1, wc = -5, wi = 4, we = 1, wo = 0, wu = -1
 1) +a, -c, +i, +e, +o, +u: Y
 Its (+a,+i+e+o+u)= (score 1+4+1+0-1 = 5)
 2) -a, +c, -i, +e, -o, -u: N (score -5+1=-4)
 Its (+c+e)=(-5+1= -4)
 And so on

49. 9/19/2017
49
 Need to set some threshold above which we predict to be
paid back (say, 2)
 May care about combinations of things (nonlinearity) –
generalization: neural networks

50. Reinforcement learning (RL)
 Originates from Dynamic Programming (DP)
 Less exact than DP since it uses experience to
change system’s parameters and/ or structure
 There are three routes you can take to work: A, B, C
 The times you took A, it took: 10, 60, 30 minutes
 The times you took B, it took: 32, 31, 34 minutes
 The time you took C, it took 50 minutes

51. 9/19/2017
51
 What should you do next?
 Exploration vs. exploitation tradeoff
 Exploration: try to explore under-explored options
 Exploitation: stick with options that look best now
 Reinforcement learning usually studied in MDPs**
 Take action, observe, reward and new state
 **MDPs: Markov Decision Processes are a
mathematical framework for modeling sequential
decision problems under uncertainty as well as
reinforcement learning problems.

52. Bayesian approach to learning
 Assume we have a prior distribution over the long term
behavior of A
 With probability .6, A is a “fast route” which:
 With prob. .25, takes 20 minutes
 With prob. .5, takes 30 minutes
 With prob. .25, takes 40 minutes
 With probability .4, A is a “slow route” which:
 With prob. .25, takes 30 minutes
 With prob. .5, takes 40 minutes
 With prob. .25, takes 50 minutes

53. 9/19/2017
53
 We travel on A once and see it takes 30 minutes
 P(A is fast | observation) = P(observation | A is fast)*P(A is
fast) / P(observation) = .5*.6/(.5*.6+.25*.4) = .3/(.3+.1) =
.75
 Convenient approach for decision theory, game theory

54. 9/19/2017
54
Thank you