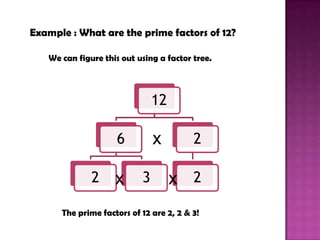
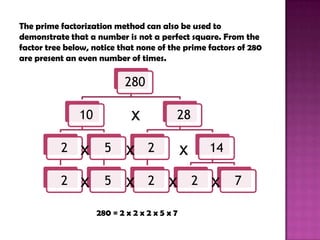
This document discusses using prime factorization to identify perfect squares. It explains that prime factorization is writing a composite number as a product of its prime factors. It then gives examples of finding the prime factors of 12 and 48. The document states that a number is a perfect square if each of its distinct prime factors occurs an even number of times in the prime factorization. It uses prime factorization to show that 64 is a perfect square since the factor 2 appears 6 times.

1. Using Prime Factorization to
Identify Perfect Squares

2. What is Prime Factorization?
Prime factorization is to write a composite
number as a product of its prime factors.
(www.northstarmath.com)
Think back . . .
A Prime Number is a whole number,
greater than 1, that can be evenly divided
only by 1 or itself.

3. Example : What are the prime factors of 12?
We can figure this out using a factor tree.
12
6 x 2
2 x 3 x 2
The prime factors of 12 are 2, 2 & 3!

4. Example : What are the prime factors of 48?
48
6 x 8
2 x 3 x 2 x 4
2 x 3 x 2 x 2 x 2
The prime factors of 48 are, 2, 2, 2, 2, & 3!

5. The prime factorization method can also be used to
demonstrate that a number is not a perfect square. From the
factor tree below, notice that none of the prime factors of 280
are present an even number of times.
280
10 x 28
2 x 5 x 2 x 14
2 x 5 x 2 x 2 x 7
280 = 2 x 2 x 2 x 5 x 7

6. A perfect square has each
distinct prime factor
occurring an even number
of times.

7. Use the Prime Factorization Method to decide if 64 is a
perfect square.
64
2 x 32
2 x 2 x 16
2 x 2 x 2 x 8
2 x 2 x 2 x 2 x 4
2 x 2 x 2 x 2 x 2 x 2
64 = 2 x 2 x 2 x 2 x 2 x 2
The factor 2 appears 6 times (an even number of time).
We can say that 64 is a perfect square because . . .

8. A perfect square has each
distinct prime factor
occurring an even number
of times.