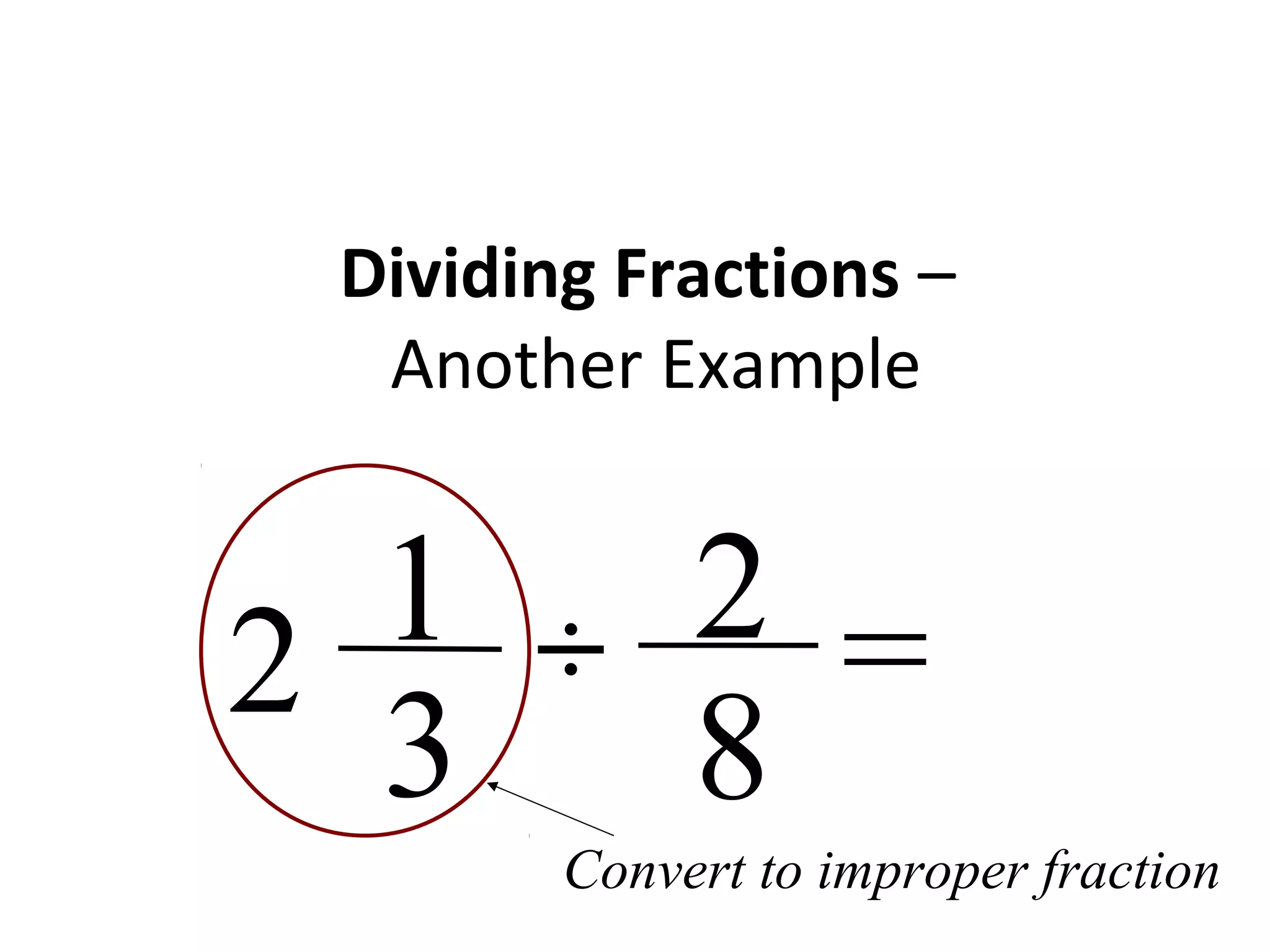
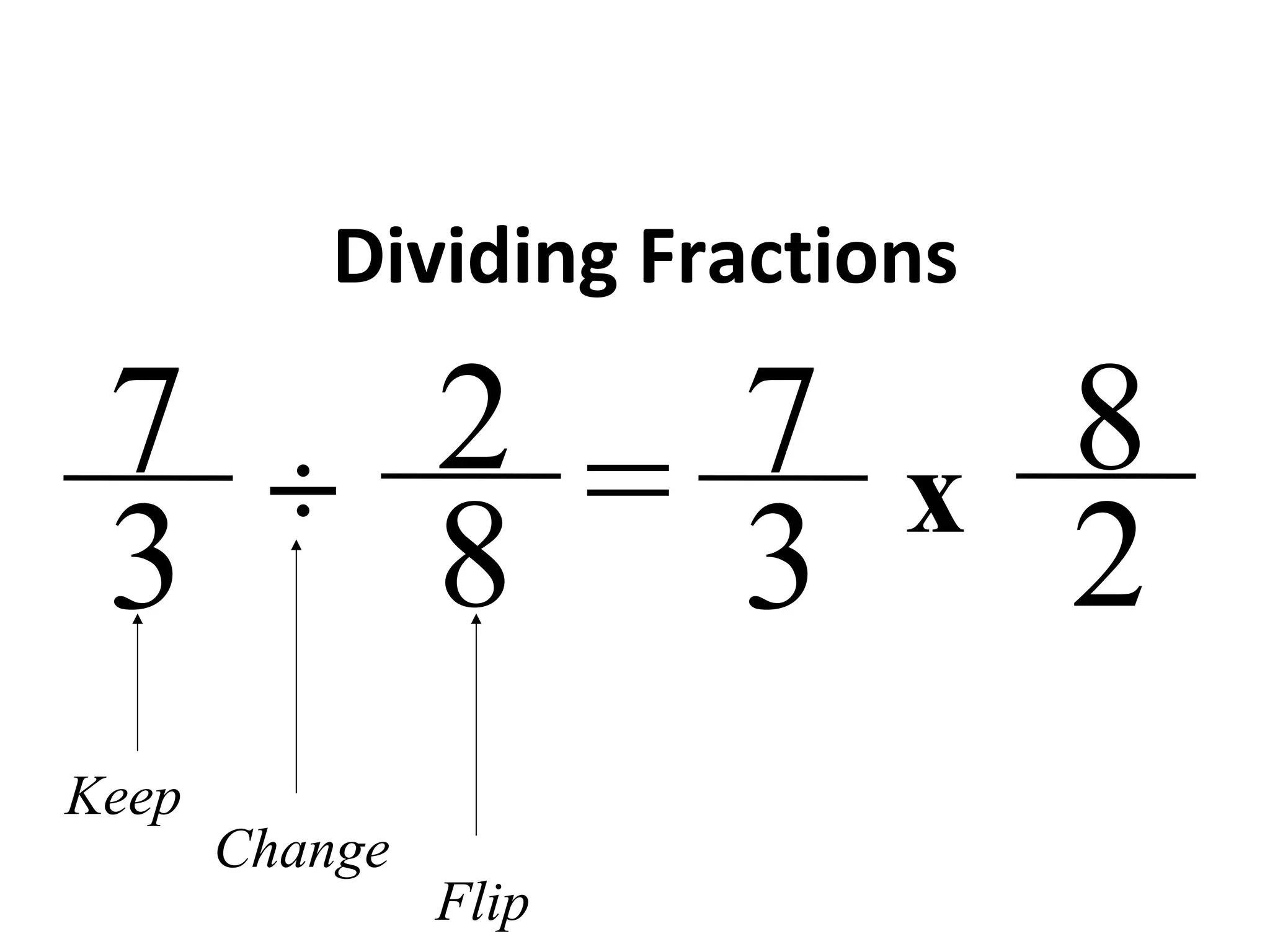
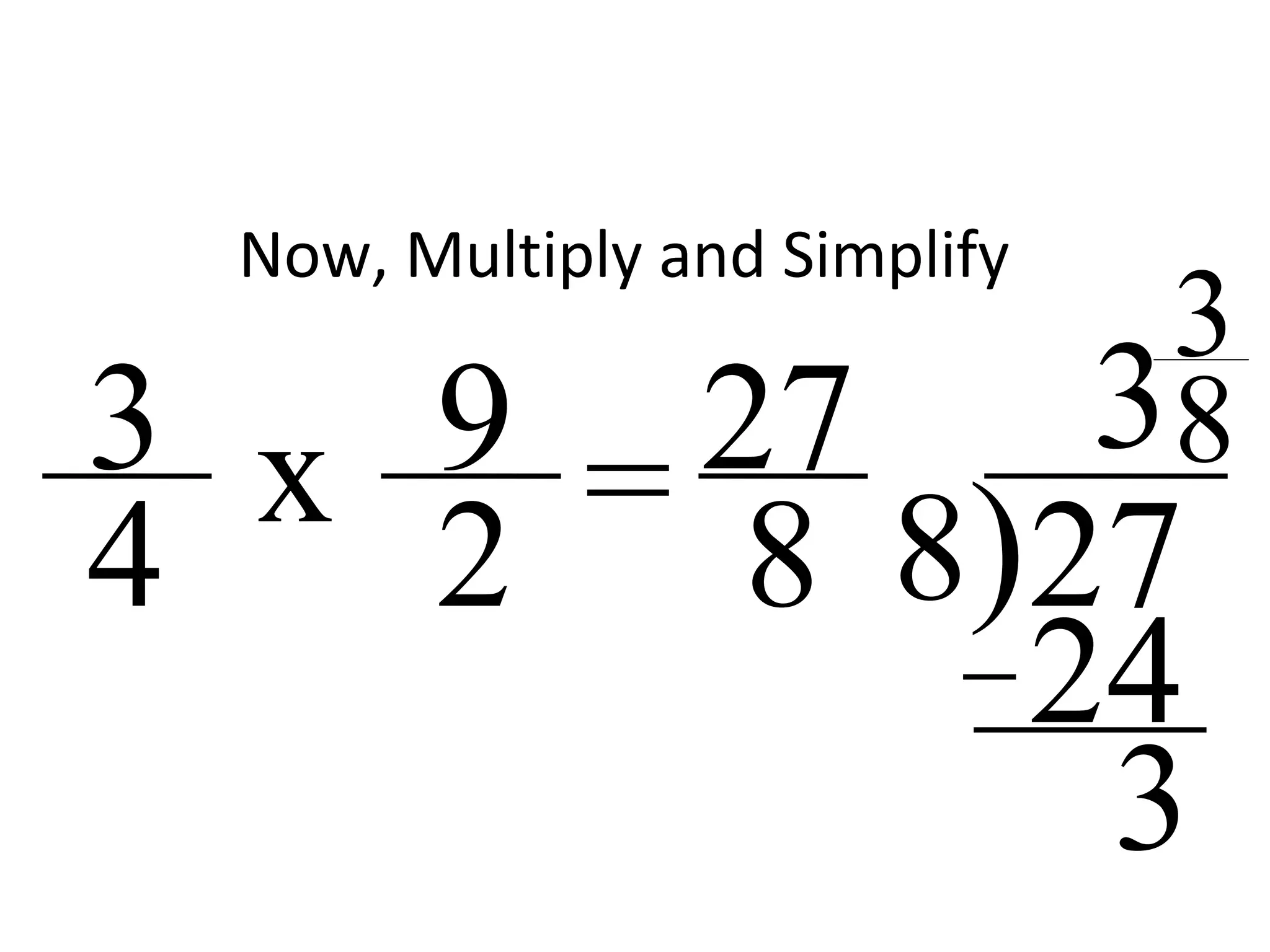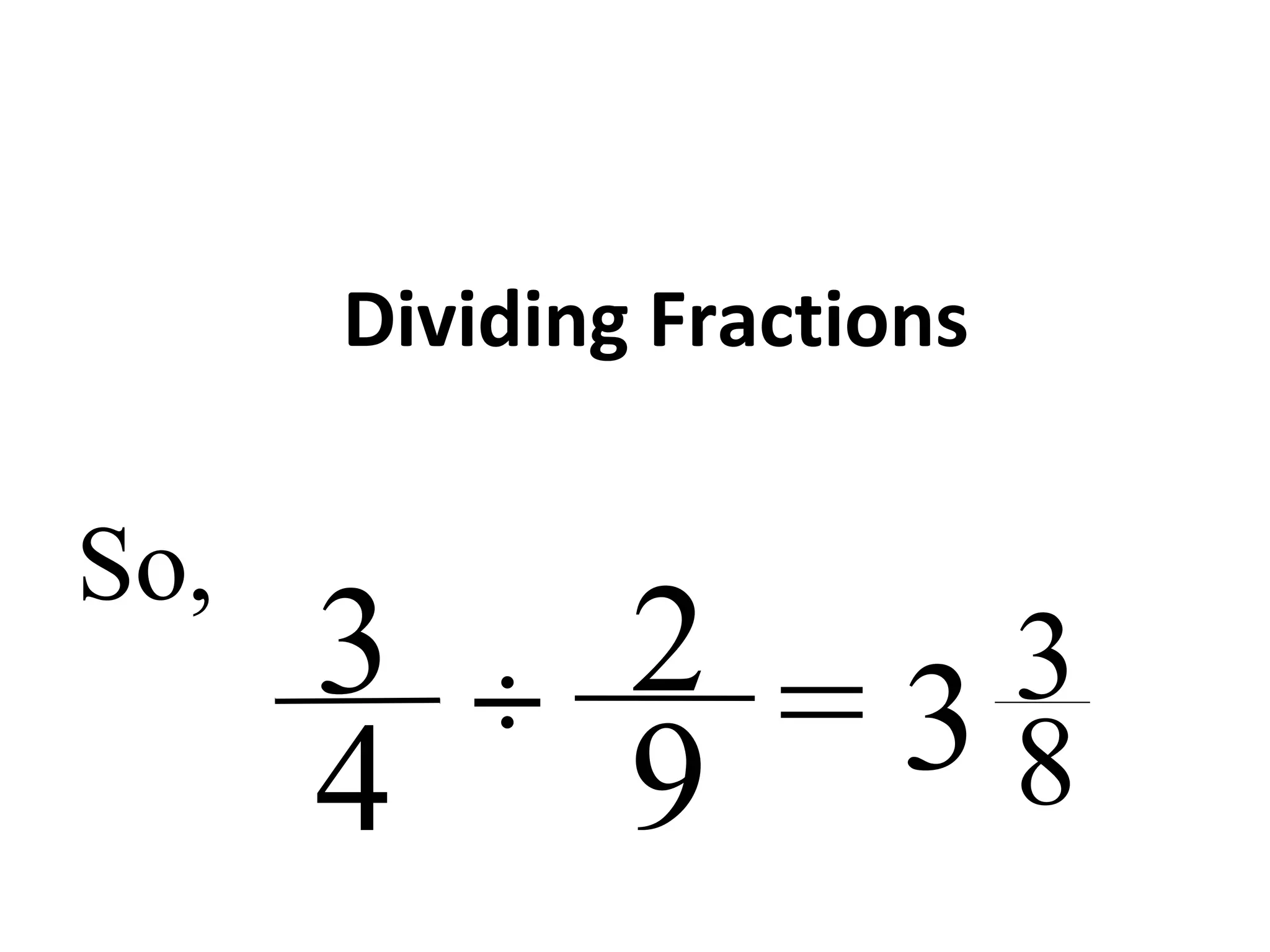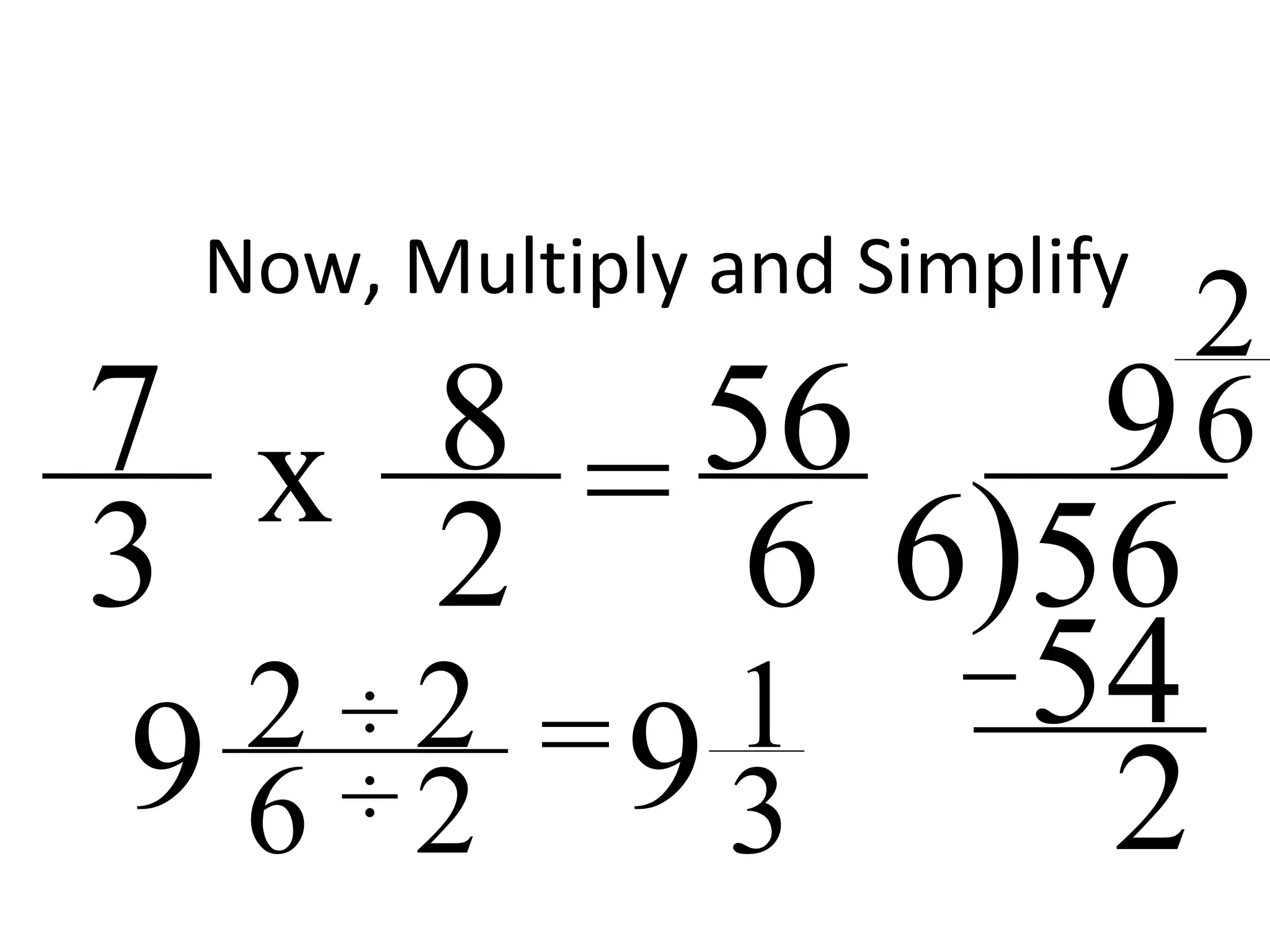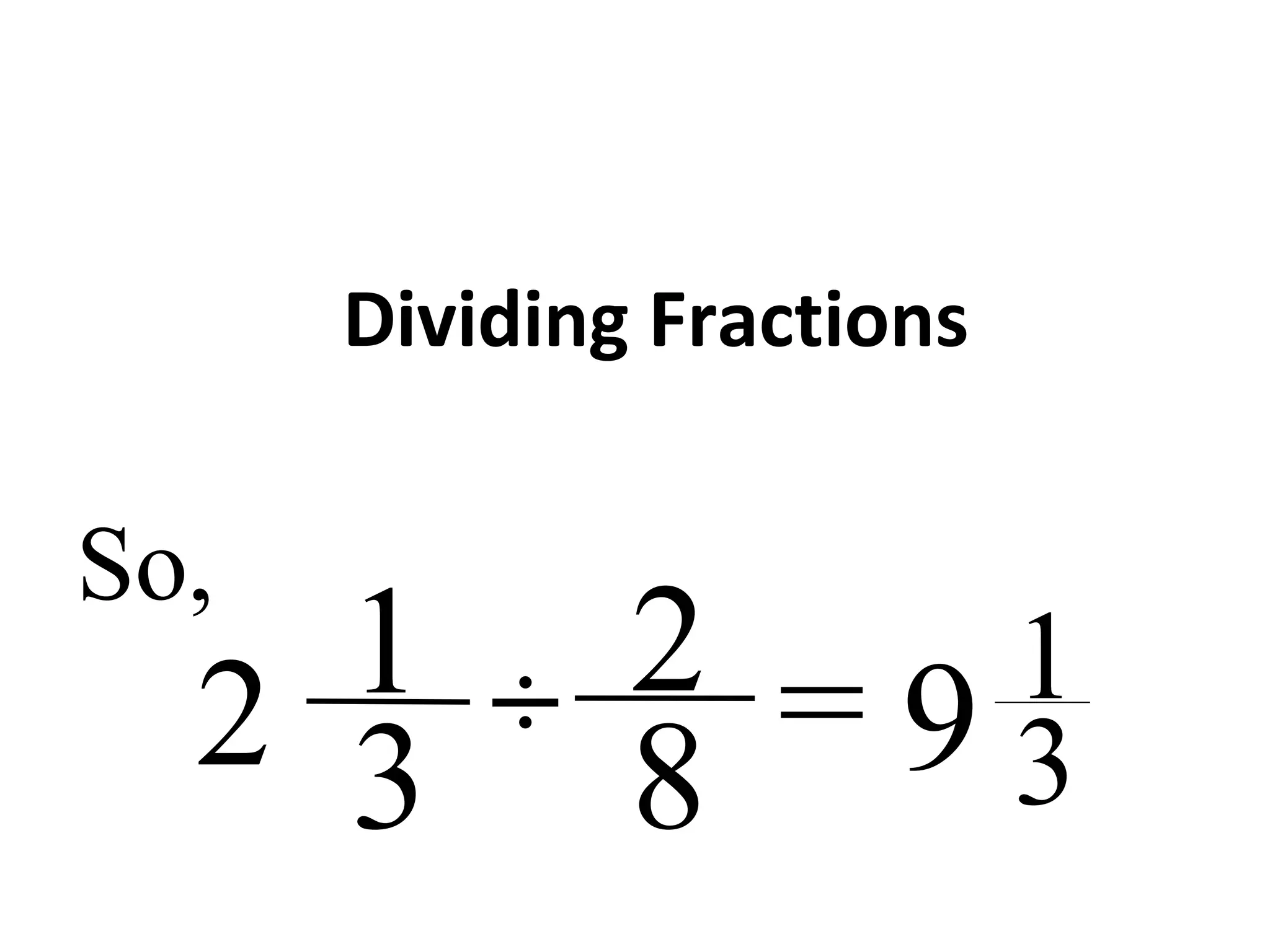This document provides instructions for dividing fractions. It begins by giving examples of dividing whole numbers and fractions. It explains that when dividing fractions between 0 and 1, the quotient will be larger than at least one of the fractions. The steps for dividing fractions are then outlined: 1) convert fractions to improper form, 2) keep the first fraction, 3) change the operation to multiplication, 4) take the reciprocal of the second fraction, 5) multiply the numerators and denominators, and 6) simplify if possible. Several examples are worked through to demonstrate the process.