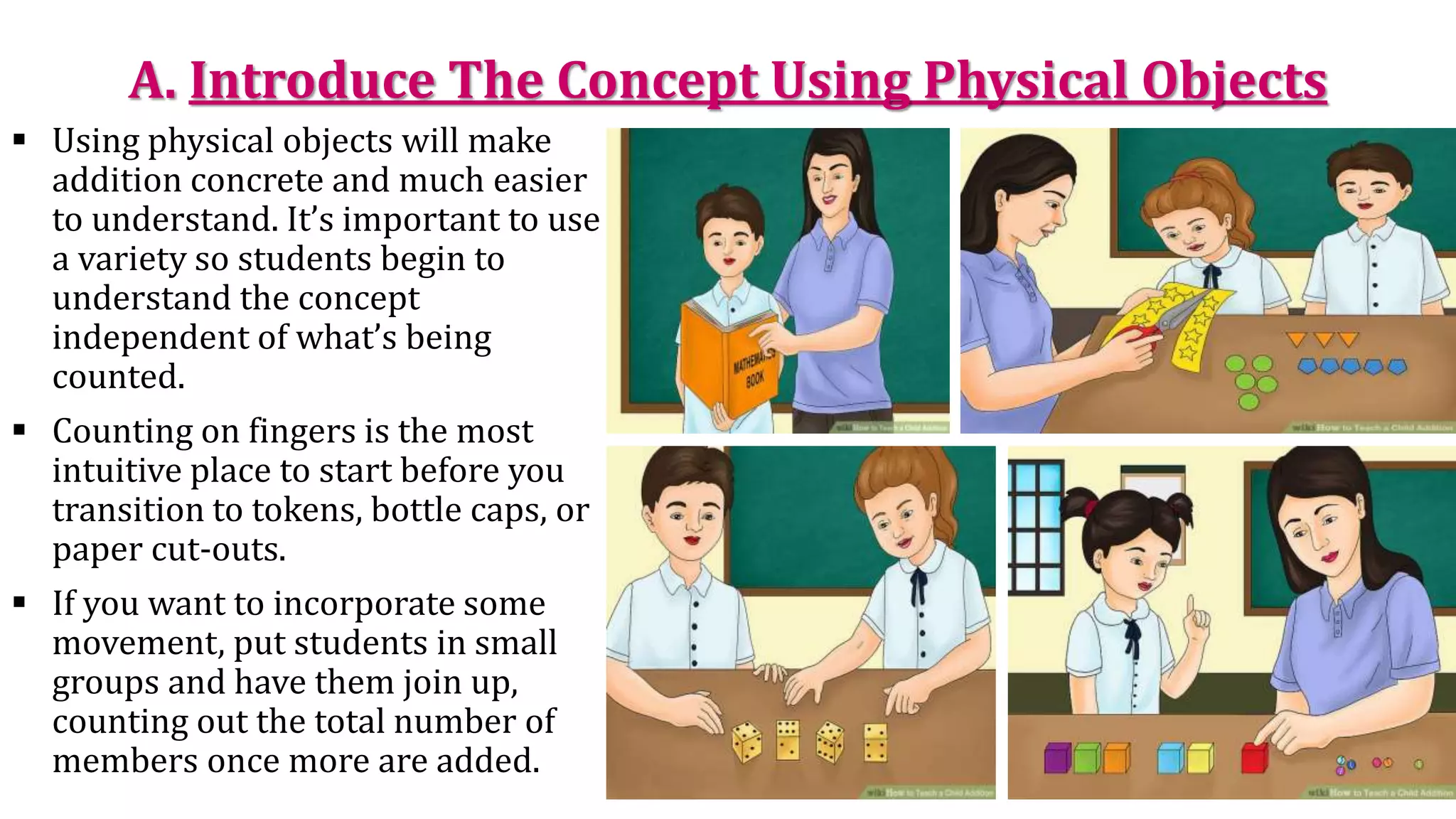
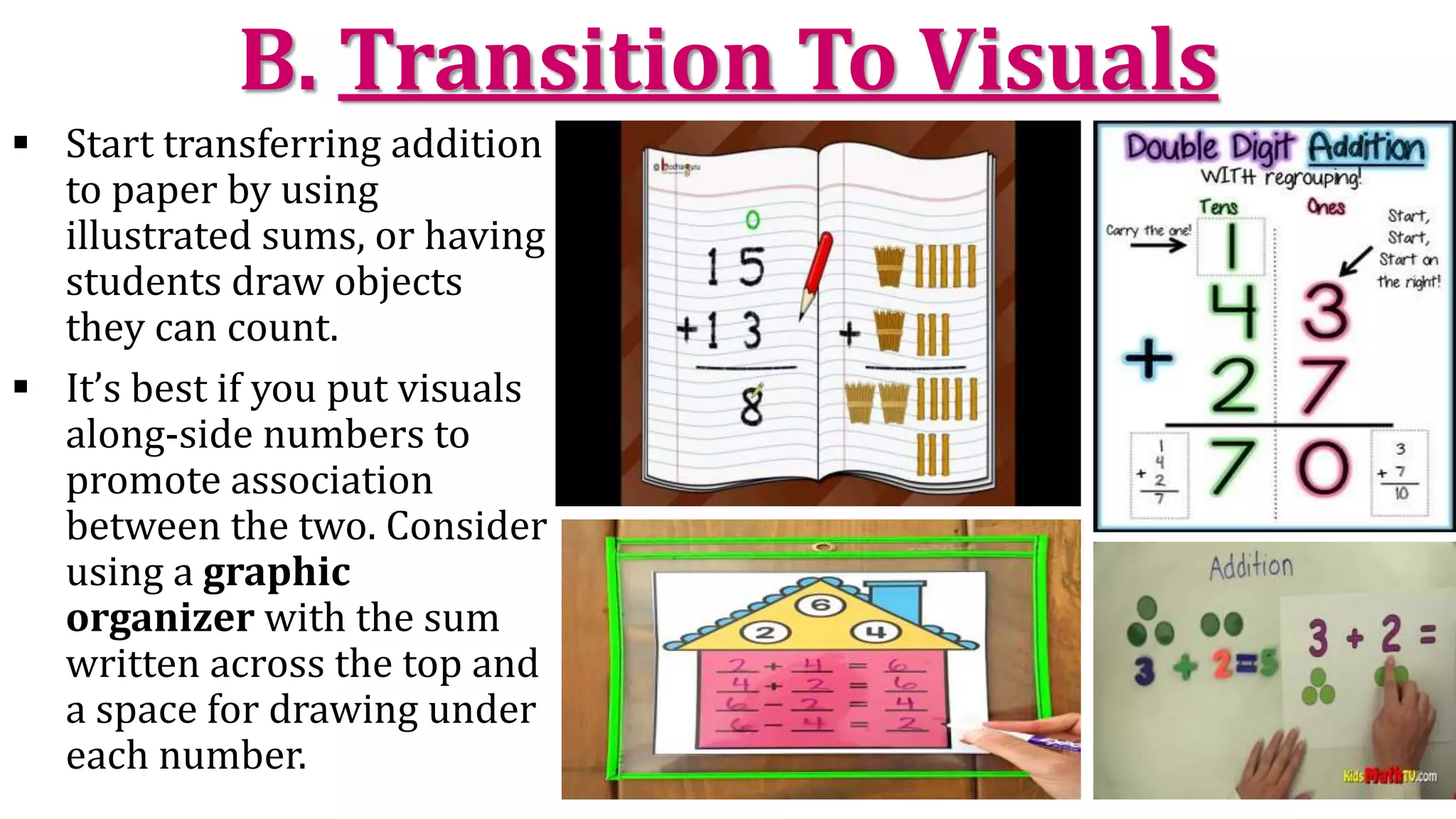
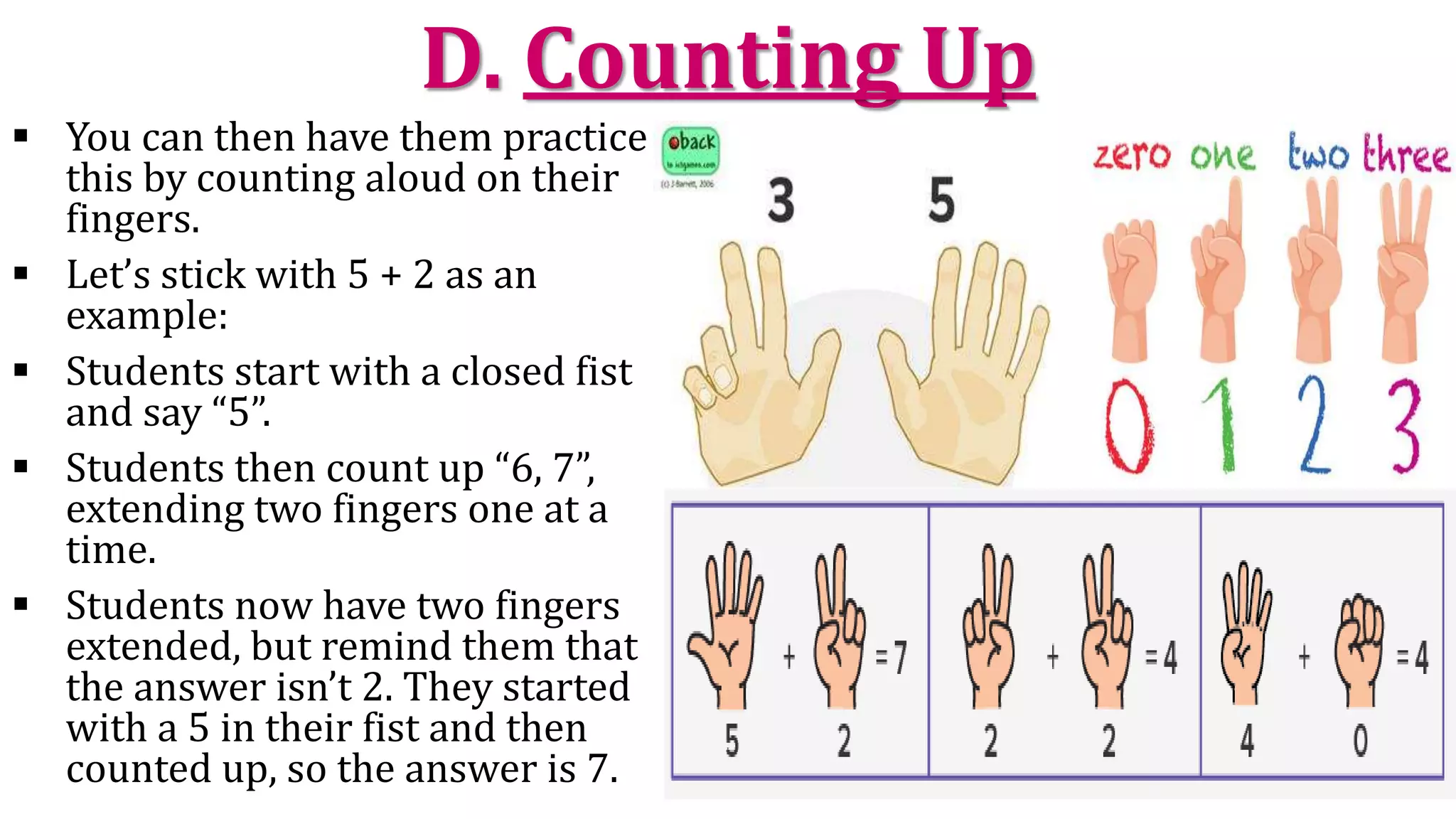
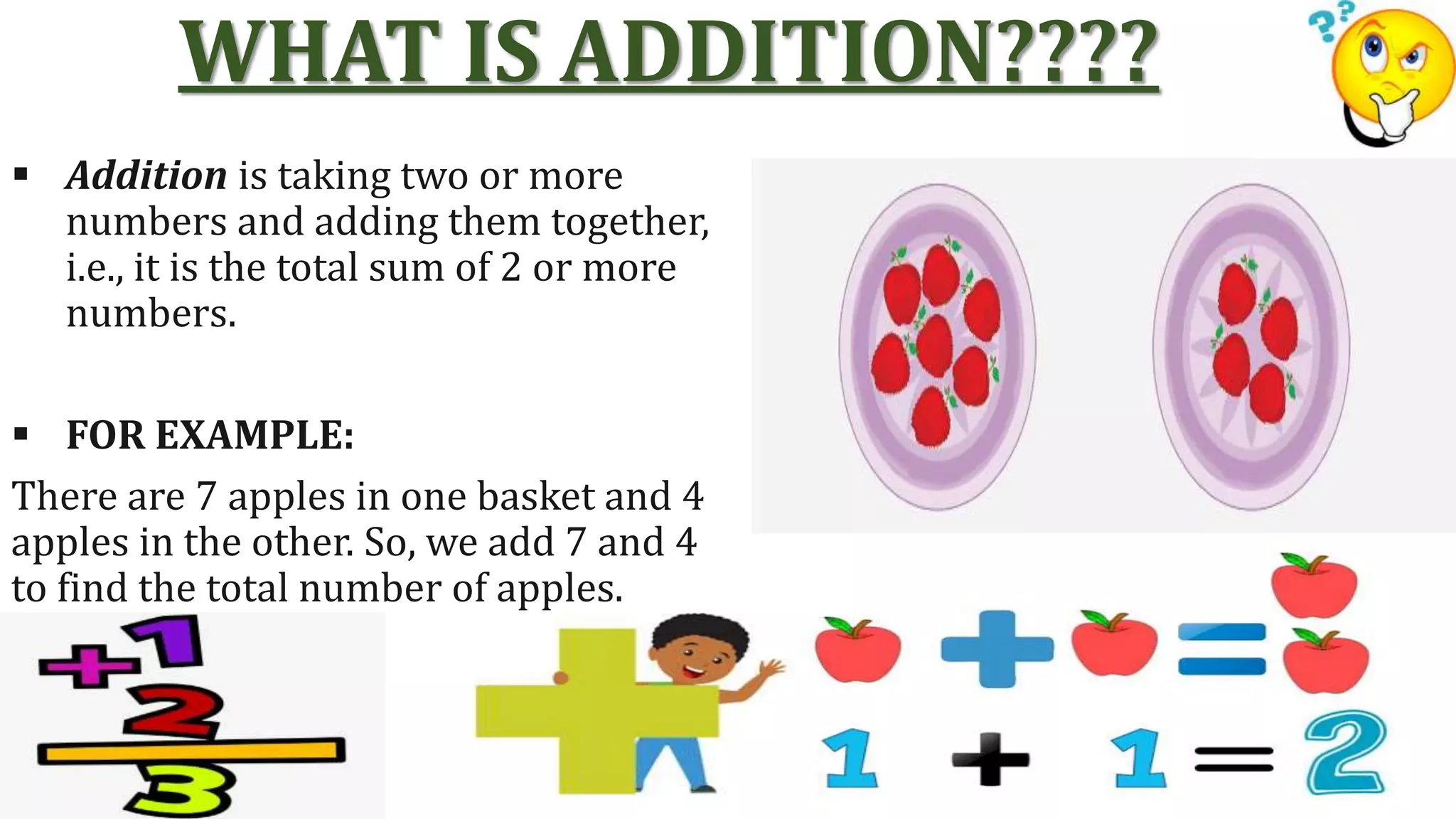
The document explains the concept of addition, defining it as the sum of two or more numbers, and details the properties of addition, including the additive identity, associative, and commutative properties. It emphasizes teaching methods such as using physical objects, visuals, number lines, and word problems to help students grasp addition effectively. The document also includes various teaching strategies and activities to reinforce these concepts.

1. CONCEPT OF ADDITION

2. WHAT IS ADDITION????
 Addition is taking two or more
numbers and adding them together,
i.e., it is the total sum of 2 or more
numbers.
 FOR EXAMPLE:
There are 7 apples in one basket and 4
apples in the other. So, we add 7 and 4
to find the total number of apples.

3. PROPERTIES OF ADDITION!!!!
 ADDITIVE IDENTITY PROPERTY
 ASSOCIATIVE PROPERTY
 COMMUTATIVE PROPERTY

4. 1. ADDITIVE IDENTITY PROPERTY
 Additive Identity is a number, which when added
to any number, gives the sum as the number
itself. It means that additive identity is “0” as
adding 0 to any number, gives the sum as the
number itself. This property is also known as
“the zero property of addition.”
 FOR EXAMPLE:
2 + 0 = 2 0 + 5 = 5
 For any set of numbers, i.e., all integers, rational
numbers, complex numbers, the additive identity
is 0. It is because when you add 0 to any number.
It doesn’t change the number and keeps its
identity.
 However, additive identity cannot be associated
to natural numbers, since 0 is not considered as a
natural number.

5. 2. ASSOCIATIVE PROPERTY
 Associative Property states that
when three or more numbers are
added, the sum is the same
regardless of the grouping of the
numbers. Associative Property gets
its name from the word “Associate”
and it refers to grouping of numbers.
 The associative property always
involves 3 or more numbers.
 The numbers that are grouped
within a bracket become one unit.
 FOR EXAMPLE:
( 2 + 3 ) + 4 = 2 + ( 3 + 4 ) = 9
 Associative property can only be
used with addition and
multiplication and not with
subtraction or division.

6. 3. COMMUTATIVE PROPERTY
 When we add two or
more whole numbers,
their sum is the same
regardless of the order
of the number is called
as “Commutative
Property.”
 FOR EXAMPLE:
2 + 1 = 1 + 2 = 3
 The sum of both 2 + 1
and 1 + 2 is 3. That
means, we can add
whole numbers in any
order.

7. LETS MOVE ON TO AN ACTIVITY!!!!

8. FIND OUT THE PROPERTIES OF ADDITION
 2+3+1=3+2+1 = ___________________
 5+0 = ___________________
 7+ [4+6] = [7+4] +6 = ________________
 8+4+2 = 4+2+8 = ___________
 0+29= _________
 8+2 = 2+8 = _________
 9+ [1+2] +4 = [9+1] +4+2 = __________
 9+ [5+1] = [9+5] +1 = __________
 100+50+1 = 50+100+1 =_________
 0+4 = 4+0 = ___________

9. METHODS OF TEACHING ADDITION......
 Introduce The Concept Using Physical Objects.
 Transition To Visuals.
 Use A Number Line.
 Counting Up.
 Finding The Ten.
 Word Problems.

10. A. Introduce The Concept Using Physical Objects
 Using physical objects will make
addition concrete and much easier
to understand. It’s important to use
a variety so students begin to
understand the concept
independent of what’s being
counted.
 Counting on fingers is the most
intuitive place to start before you
transition to tokens, bottle caps, or
paper cut-outs.
 If you want to incorporate some
movement, put students in small
groups and have them join up,
counting out the total number of
members once more are added.

11. B. Transition To Visuals
 Start transferring addition
to paper by using
illustrated sums, or having
students draw objects
they can count.
 It’s best if you put visuals
along-side numbers to
promote association
between the two. Consider
using a graphic
organizer with the sum
written across the top and
a space for drawing under
each number.

12. C. Use A Number Line
 Most students will still
be adding by counting
out every number in a
sum to reach the total
solution. A number
line, however, removes
the need to count out
the first number in the
sum.
 If the sum is 3 + 1, For
Example, students can
put their finger on the
three to start with, and
then count up ones to
reach 4.

13. D. Counting Up
 You can then have them practice
this by counting aloud on their
fingers.
 Let’s stick with 5 + 2 as an
example:
 Students start with a closed fist
and say “5”.
 Students then count up “6, 7”,
extending two fingers one at a
time.
 Students now have two fingers
extended, but remind them that
the answer isn’t 2. They started
with a 5 in their fist and then
counted up, so the answer is 7.

14. E. Finding The Ten
 Instead of adding two
numbers together as
they are, encourage
students to add them up
to 10, and then add the
remainder to that 10.
 FOR EXAMPLE,
The Process for 7 + 5 is:
7 + 3 = 10
We still need to add an
extra 2, to turn that 3 into
5.
10 + 2 = 12

15. F. Word Problems
 Word problems encourage
students to identify addition
problems even when they aren’t
clearly specified. Start by
introducing them to the language of
addition, such as:
o X Plus Y
o X Extra
o X Added To
o Total Amount
o In All
o Altogether
 Once they’re familiar with the
language, get them started with
simple problem-solving and
reasoning activities.

16. ***SOME FACTS***
 Addition of two whole numbers except for zero will
always give a bigger number.
 When you add numbers (except 0) on a number line,
the result will always shift you to the right.
 The symbol used to indicate Addition is ‘+’ (plus
symbol).
 Addition of small numbers can be done horizontally.
 Large numbers are added in vertical columns
(written under the place value chart).
 The number or values being added are called
addends and the answer is called the sum.
 1 added to a number gives the successor of the
number as the sum.
 To find a missing addend in an addition sum, the
given addend or the sum of all the given addends is
subtracted from the given sum.