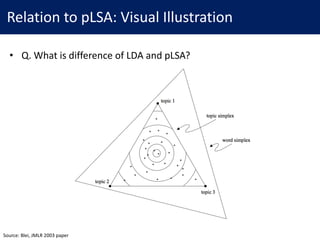
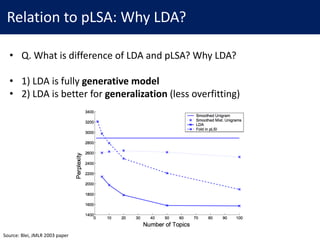
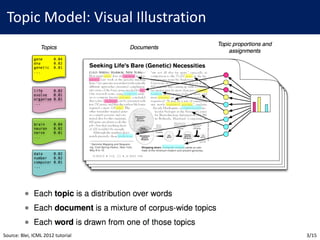
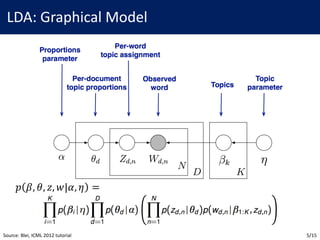
This document provides an overview of Latent Dirichlet Allocation (LDA), a generative probabilistic model for collections of discrete data such as text corpora. It defines key terminology for LDA including documents, words, topics, and distributions. The document then explains LDA's graphical model and generative process, which represents documents as mixtures over latent topics and generates words probabilistically from topics. Variational inference is introduced as an approach for approximating the intractable posterior distribution over topics and learning model parameters.

1. Latent Dirichlet Allocation
2017.05.08.
Sangwoo Mo
1/15

2. Topic Model: Terminology
• Document Model
• Word: element in vocabulary set
• Document: collection of words
• Corpus: collection of documents
• Topic Model
• Topic: collection of words (subset of vocabulary)
• Document is represented by (latent) mixture of topics
• 𝑝 𝑤 𝑑 = 𝑝 𝑤 𝑧 𝑝(𝑧|𝑑) (𝑧: topic)
• Note: document is collection of words (not sequence)
• We call it bag-of-words assumption
• In probability, we call it exchangeability assumption
• 𝑝 𝑤), … , 𝑤, = 𝑝(𝑤- ) , … , 𝑤- , ) (𝜎: permutation)
2/15

3. Topic Model: Visual Illustration
Source: Blei, ICML 2012 tutorial 3/15

4. Topic Model: Why we study it?
• For given corpus, we learn two things
• 1) Topic: from full vocabulary set, we learn important subsets
• 2) Topic proportion: for each document, we learn what is it about
• It can be viewed as dimensionality reduction
• From large vocabulary set, extract basis vectors (topic)
• Represent document in topic space (topic proportion)
• Here, dimension is reduced from 𝑤/ ∈ ℤ2
,
to 𝜃 ∈ ℝ5
• We may use topic proportion to other applications
• e.g. document classification (using 𝜃 as feature)
4/15

5. LDA: Graphical Model
Source: Blei, ICML 2012 tutorial
𝑝 𝛽, 𝜃, 𝑧, 𝑤|𝛼, 𝜂 =
5/15

6. LDA: Generative Process
• 𝜂 ∈ ℝ2, 𝛼 ∈ ℝ5 are model parameters
• For 𝑖 in 1, 𝐾 :
• Choose per-corpus topic distribution 𝛽< ∈ ℝ2 ∼ Dir(𝜂)
• For 𝑖 in 1, 𝐷 :
• Choose per-document topic proportion 𝜃B ∈ ℝ5 ∼ Dir(𝛼)
• For 𝑗 in 1, 𝑁B :
• Choose topic 𝑧B,E ∈ ℤ5 ∼ Multinomial 𝜃B
• Choose word 𝑤B,E ∈ ℤ2 ∼ Multinomial(𝑤B,E|𝑧B,E, 𝛽<)
6/15

7. Aside: Dirichlet Distribution
• Dirichlet distribution is conjugate prior of Multinomial
𝑝 𝜃 𝛼 =
Γ(∑ 𝛼/
<
/P) )
∏ Γ(𝛼/)<
/P)
𝜃)
RST)
⋯ 𝜃<
RVT)
• The parameter 𝛼 controls the shape and sparsity of 𝜃
• high 𝛼 = uniform 𝜃, small 𝛼 = sparse 𝜃
𝛼 = 100 𝛼 = 10 𝛼 = 1 𝛼 = 0.1 𝛼 = 0.01
Source: Blei, ICML 2012 tutorial 7/15

8. LDA: Inference
• Recall:
• Find MAP assignment of latent variables
𝑝 𝛽, 𝜃, 𝑧 𝑤, 𝛼, 𝜂 =
𝑝(𝛽, 𝜃, 𝑧, 𝑤|𝛼, 𝜂)
∫ ∫ ∑ 𝑝(𝛽, 𝜃, 𝑧, 𝑤|𝛼, 𝜂)[]
• Posterior is intractable; We use techniques e.g. MCMC, VI, etc.
• Today, I will only introduce variational inference
8/15

9. LDA: Variational Inference
• Variational Inference (mean field approximation)
• Approximate 𝑝(𝛽, 𝜃, 𝑧|𝑤, 𝛼, 𝜂) with 𝑞(𝛽, 𝜃, 𝑧|𝜆, 𝛾, 𝜑) where
𝑞 𝛽, 𝜃, 𝑧 𝜆, 𝛾, 𝜑 = ∏𝑞 𝛽< 𝜆< ∏ 𝑞 𝜃B 𝛾B ∏𝑞 𝑧B,E 𝜑B,E
Source: Hockenmaier, CS598 Advanced NLP lecture #7 9/15

10. LDA: Variational Inference
• Approximate 𝑝(𝛽, 𝜃, 𝑧|𝑤, 𝛼, 𝜂) with 𝑞(𝛽, 𝜃, 𝑧|𝜆, 𝛾, 𝜑) where
𝑞 𝛽, 𝜃, 𝑧 𝜆, 𝛾, 𝜑 = ∏𝑞 𝛽< 𝜆< ∏ 𝑞 𝜃B 𝛾B ∏𝑞 𝑧B,E 𝜑B,E
• Goal: Minimize 𝐾𝐿(𝑞||𝑝) over (𝜆, 𝛾, 𝜑)
• However, 𝐾𝐿(𝑞||𝑝) is intractable since
𝑝 𝛽, 𝜃, 𝑧 𝑤, 𝛼, 𝜂 =
𝑝(𝛽, 𝜃, 𝑧, 𝑤|𝛼, 𝜂)
∫ ∫ ∑ 𝑝(𝛽, 𝜃, 𝑧, 𝑤|𝛼, 𝜂)[]
is intractable; Thus, we optimize alternative objective
10/15

11. LDA: Variational Inference
• Recall: Want to minimize 𝐾𝐿(𝑞||𝑝), but it is intractable
• Alternative Goal: Maximize ELBO 𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 where
𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 = 𝐸f log 𝑝 𝛽, 𝜃, 𝑧, 𝑤 𝛼, 𝜂 − 𝐸f[log 𝑞(𝛽, 𝜃, 𝑧|𝛼, 𝜂)]
• Since log 𝑝(𝑤|𝛼, 𝜂) = 𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 + 𝐾𝐿(𝑞||𝑝),
minimizing 𝐾𝐿(𝑞||𝑝) is equal to maximizing 𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂
11/15

12. LDA: Variational Inference
• Maximize ELBO 𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 where
𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 = 𝐸f log 𝑝 𝛽, 𝜃, 𝑧, 𝑤 𝛼, 𝜂 − 𝐸f[log 𝑞(𝛽, 𝜃, 𝑧|𝛼, 𝜂)]
• Final Goal: maximize 𝐿 𝜆, 𝛾, 𝜑; 𝛼, 𝜂 over 𝜆, 𝛾, 𝜑, 𝛼, 𝜂
• Idea: divide hard problem into two (relatively) easy problems
• 1) maximize 𝐿 𝜆, 𝛾, 𝜑, 𝛼, 𝜂 over 𝜆, 𝛾, 𝜑
• 2) maximize 𝐿 𝜆, 𝛾, 𝜑, 𝛼, 𝜂 over (𝛼, 𝜂)
Source: Hockenmaier, CS598 Advanced NLP lecture #7 12/15

13. LDA: Variational EM
• Variational EM (EM: Expectation Maximization)
• E-step: optimize local parameter 𝜆, 𝛾, 𝜑 (w.r.t. 𝛼, 𝜂)
• M-step: optimize global parameter 𝛼, 𝜂 (w.r.t. 𝜆, 𝛾, 𝜑)
Source: Blei, NIPS 2016 tutorial 13/15

14. LDA: Variational EM
• Variational EM (EM: Expectation Maximization)
• E-step: optimize local parameter 𝜆, 𝛾, 𝜑 (w.r.t. 𝛼, 𝜂)
• M-step: optimize global parameter 𝛼, 𝜂 (w.r.t. 𝜆, 𝛾, 𝜑)
• Each subproblem is simple one-variable constraint optimization
• We can solve it by taking derivative of Lagrangian to zero1
• e.g. optimize 𝐿 over 𝜑 (since 𝜑 ∼ Multinomial, ∑ 𝜑E/
5
/P) = 1)
1. In fact, 𝐿[l] cannot be solved analytically. Authors suggest to use Netwon-Raphson method for efficient implementation.
See A.3 and A.4 of Blei 2003 for detail.
Source: Blei, JMLR 2003 paper 14/15

15. LDA: Variational EM
• Variational EM (EM: Expectation Maximization)
• E-step: optimize local parameter 𝜆, 𝛾, 𝜑 (w.r.t. 𝛼, 𝜂)
• M-step: optimize global parameter 𝛼, 𝜂 (w.r.t. 𝜆, 𝛾, 𝜑)
Source: Hockenmaier, CS598 Advanced NLP lecture #7 15/15

16. Appendix

17. Relation to pLSA: Graphical Model
• Q. What is difference of LDA and pLSA?
Source: Blei, JMLR 2003 paper

18. Relation to pLSA: Visual Illustration
• Q. What is difference of LDA and pLSA?
Source: Blei, JMLR 2003 paper

19. Relation to pLSA: Why LDA?
• Q. What is difference of LDA and pLSA? Why LDA?
• 1) LDA is fully generative model
• Caveat: but we cannot use LDA to generate document
since it only generates bag-of-words, not sequence
• 2) LDA is better for generalization (less overfitting)
• LDA is generalization of pLSA (pLSA = LDA w/ uniform prior)
• pLSA has 𝐾𝑉 + 𝐾𝑁 parameters, but LDA has 𝐾𝑉 + 𝐾

20. Relation to pLSA: Why LDA?
• Q. What is difference of LDA and pLSA? Why LDA?
• 1) LDA is fully generative model
• 2) LDA is better for generalization (less overfitting)
Source: Blei, JMLR 2003 paper

21. ELBO (Evidence Lower Bound)
Source: Blei, JMLR 2003 paper

22. de Finetti's theorem
• Q. We only assumed exchangeability (not i.i.d.)
𝑝 𝑤), … , 𝑤, = 𝑝(𝑤- ) , … , 𝑤- , ) (𝜎: permutation)
• Why is it reasonable to factorize 𝑝 𝑤 𝛽, 𝑧 ? ⇒ de Finetti’s theorem!
• Statement: Exchangeable r.v. is mixture of conditional i.i.d. r.v.s
• Since word is generated by topic (fixed conditional distribution)
and topic is exchangeable within document, by de Finetti’s thm,
there is (mixture proportion) 𝑝(𝜃) s.t.
𝑝 𝑤, 𝑧 = ∫ 𝑝 𝜃 ∏𝑝 𝑧E 𝜃 𝑝 𝑤E 𝑧E 𝑑𝜃