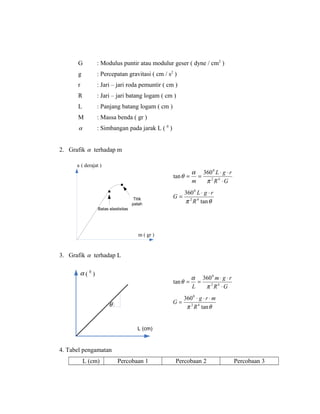
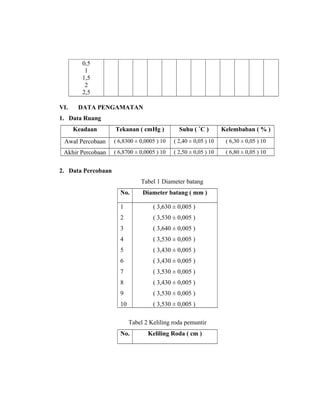
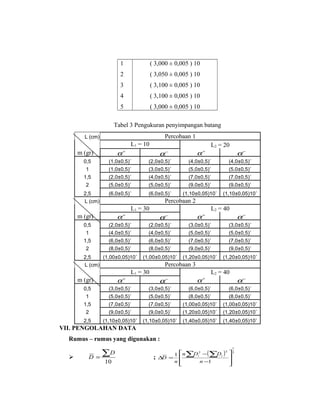
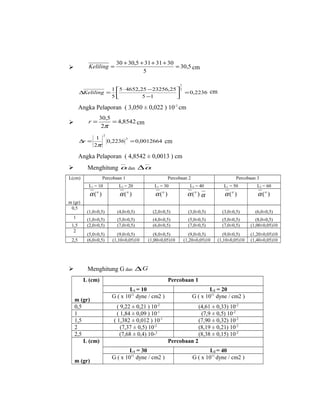
Dokumen ini membahas tentang percobaan untuk menentukan modulus puntir batang logam dengan menggunakan alat pemuntir dan berbagai alat ukur. Teori yang dijelaskan mencakup hubungan antara gaya, simpangan, dan parameter fisik lainnya, serta cara melakukan pengamatan dan pengolahan data. Selain itu, prosedur percobaan dan rumus-rumus yang digunakan untuk analisis data juga dijabarkan secara rinci.

1. I. MAKSUD
1. Mengamati bahwa puntiran diteruskan pada arah memanjang.
2. Menentukan modulus puntir batang logam.
II. ALAT
1. Alat pemuntir
2. micrometer sekrup
3. jangka sorong
4. mistar gulung
5. beban
III. TEORI
Bila sebatang logam pejal dengan panjang L dan jari-jari R, salah satu ujungnya
dijepit dan ujung yang lain dipuntir dengan gaya F, maka akan terjadi
simpangan atau pergeseran sebesar α˚ (lihat gambar 1).
Gambar 1.
Besar pergeseran (α˚) untuk setiap logam berbeda-beda, tergantung koefisien
kekenyalannya. Hubungan tersebut dinyatakan sebagai berikut :
2 ML
G= ......................................................……………………………..... (1)
πθR 4
Atau
360 ⋅ g ⋅ r ⋅ L ⋅ m
G= ………………...............................................…………. (2)
π 2 R 4α

2. Dengan :
G = modulus puntir (modulus geser = koefisien kekenyalan)
g = percepatan gravitasi
R = jari-jari batang
L = panjang batang dari penjepit ke jarum petunjuk sekala
m = massa beban yang menyebabkan puntiran
α˚ = besar simpangan pada jarak L
r = jari-jari roda pemuntir
M = momen gaya
θ = sudut punter dalan rad
Catatan tambahan :
• Modulus Geser atau adalah bilangan yag menggambarkan perubahan benda
yang elastis, atau suatu konstanta yang menyatakan besarnya gaya yang
diperlukan untuk memuntir suatu bahan per satuan luar tiap satu derajat.
• Modulus Young adalah perbandingan regangan terhadap regangan ke satu
arah.
• Modulus Bulk adalah perbandingan regangan terhadap regangan ke segala
arah.
• Berikut adalah grafik hubungan variabel – variabel yang dipakai :

3. • Maksudnya puntiran diteruskan kearah memanjang pada tujuan percobaan
adalah bahwa di semua tempat di sepanjang batang mengalami puntiran.
• Saat pembebanan, batang tidak boleh melengkung karena salah satu syarat
dari percobaan ini dalah di setiap bagian batang harus sama partikelnya.
Kalau melengkung berarti partikel didalamnya tidak sama.
• Tegangan adalah gaya yang terjadi per satuan luas penampang. Tegangan
berlawanan arah dengan arah gayanya.
• Regangan adalah rasio antara perubahan panjanga dengan panjang mula –
mulanya dimana pada regangan akan searah dengan arah gayanya.
• Momen gaya semakin besar bila titik pusat semakin mendekati pinggiran.
IV. TUGAS PENDAHULUAN
1. Buktikan rumus (2) dan sebutkan besaran-besarannya dalam SI.
2. Gambarkan grafik α˚ terhadap massa m (dari rumus) dan terngakan cara
mendapatkan G dari grafik tersebut.
3. Gambarkan grafik α˚ terhadap jarak jarum penunjuk ke ujung yang dijepit L
(dari rumus) dan terangkan cara mendapatkan G dari grafik tersebut.
4. Buatlah tabel ( kosong ) yang hendak dipakai pada pengamatan.
Jawaban :

4. 1. Bila sebatang logam akan diselidiki adalah L. Diamati dari bagian batangnya,
bila dipuntir oleh alat pemuntir, maka puntiran yang terjadi sejauh :
R ⋅θ
F= ; dimana R = jari – jari busur lingkaran
L
∆x F
Regangan geser = = tan θ dan Tegangan Geser =
L A
Tegangangeser F A F A
Modulus geser ( G ) = Re gangangeser = ∆x L = θ
Batang :
Diketahui : ∆x = R ⋅ θ
R ⋅θ
Regangan geser =
L
∂F
Tegangan geser =
2πR ⋅ ∂R
∂τ
Torsi : ∂τ = R ⋅ ∂F ∂F =
R
Maka :
∂F 2πR ⋅ ∂R L ⋅ ∂F L ⋅ ∂τ
G= = =
R ⋅θ L 2πR ⋅ R ⋅ θ ⋅ ∂R 2πR 3 ⋅ θ ⋅ ∂R
R τ
G ⋅ 2πR 3 ⋅ θ ⋅ ∂R = L∂τ G ⋅ 2πθ ∫ R 3 ⋅ ∂R = L ∫ ∂τ
0 0
2 2 Lτ
G ⋅ ⋅ R 4πθ = Lτ G= ( rumus 1 terbukti)
4 πθ ⋅ R 4
π
Diketahui : θ rad = ×α
180
τ = F ⋅r = m⋅ g ⋅r
Maka didapat rumus :
360 0 L ⋅ M ⋅ g ⋅ r
G= ( rumus 2 terbukti )
π 2 R 4α 0
Keterangan :

5. G : Modulus puntir atau modulur geser ( dyne / cm2 )
g : Percepatan gravitasi ( cm / s2 )
r : Jari – jari roda pemuntir ( cm )
R : Jari – jari batang logam ( cm )
L : Panjang batang logam ( cm )
M : Massa benda ( gr )
α : Simbangan pada jarak L ( 0 )
2. Grafik α terhadap m
a ( derajat )
α 360 0 L ⋅ g ⋅ r
. . tan θ =
m
=
π 2R4 ⋅G
360 0 L ⋅ g ⋅ r
Titik G=
patah π 2 R 4 tan θ
Batas elastisitas
m ( gr )
3. Grafik α terhadap L
α(0)
α 360 0 m ⋅ g ⋅ r
tan θ = =
L π 2R4 ⋅G
360 0 ⋅ g ⋅ r ⋅ m
θ G=
π 2 R 4 tan θ
L (cm)
4. Tabel pengamatan
L (cm) Percobaan 1 Percobaan 2 Percobaan 3

6. L1 = 10 L2 = 20 L1 = 30 L2 = 40 L1 = 50 L2 = 60
m (gr) α + α− α + α− α + α− α + α− α + α− α + α−
0,5
1
1,5
2
2,5
V. PERCOBAAN YANG HARUS DILAKUKAN
1. Ukurlah garis tengah batang pada beberapa tempat dengan arahpengukuran
yang berbeda-beda.
2. Pasang batang logam yang akan diselidiki pada alat pemuntir. Keraskan
sekrup-sekrup seperlunya.
3. Pasang jarum penunjuk pada jarak tertentu dari ujung penjepit (10, 20, 30,
40, 50, 60 cm ).
4. Atur sedemikian rupa sehingga poros batang tepat pada poros skala busur
pengukur.
5. Berilah pembebanan awal sehingga tali pemutar tegang, tunggu sesaat dan
amati kedudukan jarum pemutar.
6. Berilah berturut-turut pembebanan tambahan, tunggu sesaat dan amatilah
kedudukan jarum penunjuk (dicatat dalam bentuk table).
7. Lakukan pengurangan beban secara berturut-turut dan amati kedudukan
jarum penunjuk (apakah kembali pada posisi semula).
8. Ulangi langkah V.3 sampai V.7 untuk kedudukan jarum yang berbeda-beda.
9. Ulangi seluruh percobaan V dengan batang logam yang lain.
L (cm) Percobaan 1 Percobaan 2 Percobaan 3
L1 = 10 L2 = 20 L1 = 30 L2 = 40 L1 = 50 L2 = 60
m (gr) α + α− α + α− α + α− α + α− α + α− α + α−

7. 0,5
1
1,5
2
2,5
VI. DATA PENGAMATAN
1. Data Ruang
Keadaan Tekanan ( cmHg ) Suhu ( ˚C ) Kelembaban ( % )
Awal Percobaan ( 6,8300 ± 0,0005 ) 10 ( 2,40 ± 0,05 ) 10 ( 6,30 ± 0,05 ) 10
Akhir Percobaan ( 6,8700 ± 0,0005 ) 10 ( 2,50 ± 0,05 ) 10 ( 6,80 ± 0,05 ) 10
2. Data Percobaan
Tabel 1 Diameter batang
No. Diameter batang ( mm )
1 ( 3,630 ± 0,005 )
2 ( 3,530 ± 0,005 )
3 ( 3,640 ± 0,005 )
4 ( 3,530 ± 0,005 )
5 ( 3,430 ± 0,005 )
6 ( 3,430 ± 0,005 )
7 ( 3,530 ± 0,005 )
8 ( 3,430 ± 0,005 )
9 ( 3,530 ± 0,005 )
10 ( 3,530 ± 0,005 )
Tabel 2 Keliling roda pemuntir
No. Keliling Roda ( cm )

8. 1 ( 3,000 ± 0,005 ) 10
2 ( 3,050 ± 0,005 ) 10
3 ( 3,100 ± 0,005 ) 10
4 ( 3,100 ± 0,005 ) 10
5 ( 3,000 ± 0,005 ) 10
Tabel 3 Pengukuran penyimpangan batang
L (cm) Percobaan 1
L1 = 10 L2 = 20
m (gr) α +
α −
α +
α−
0,5 (1,0±0,5)˚ (2,0±0,5)˚ (4,0±0,5)˚ (4,0±0,5)˚
1 (1,0±0,5)˚ (3,0±0,5)˚ (5,0±0,5)˚ (5,0±0,5)˚
1,5 (2,0±0,5)˚ (4,0±0,5)˚ (7,0±0,5)˚ (7,0±0,5)˚
2 (5,0±0,5)˚ (5,0±0,5)˚ (9,0±0,5)˚ (9,0±0,5)˚
2,5 (6,0±0,5)˚ (6,0±0,5)˚ (1,10±0,05)10˚ (1,10±0,05)10˚
L (cm) Percobaan 2
L1 = 30 L2 = 40
m (gr) α +
α −
α +
α−
0,5 (2,0±0,5)˚ (2,0±0,5)˚ (3,0±0,5)˚ (3,0±0,5)˚
1 (4,0±0,5)˚ (4,0±0,5)˚ (5,0±0,5)˚ (5,0±0,5)˚
1,5 (6,0±0,5)˚ (6,0±0,5)˚ (7,0±0,5)˚ (7,0±0,5)˚
2 (8,0±0,5)˚ (8,0±0,5)˚ (9,0±0,5)˚ (9,0±0,5)˚
2,5 (1,00±0,05)10˚ (1,00±0,05)10˚ (1,20±0,05)10˚ (1,20±0,05)10˚
L (cm) Percobaan 3
L1 = 30 L2 = 40
m (gr) α +
α −
α +
α−
0,5 (3,0±0,5)˚ (3,0±0,5)˚ (6,0±0,5)˚ (6,0±0,5)˚
1 (5,0±0,5)˚ (5,0±0,5)˚ (8,0±0,5)˚ (8,0±0,5)˚
1,5 (7,0±0,5)˚ (7,0±0,5)˚ (1,00±0,05)10˚ (1,00±0,05)10˚
2 (9,0±0,5)˚ (9,0±0,5)˚ (1,20±0,05)10˚ (1,20±0,05)10˚
2,5 (1,10±0,05)10˚ (1,10±0,05)10˚ (1,40±0,05)10˚ (1,40±0,05)10˚
VII. PENGOLAHAN DATA
Rumus – rumus yang digunakan :
1
 D =
∑D ; 1 n ∑ i −(∑ i )
∆ = 
D
D2 D
2
2

10 n n −1 
 

9. 1 1
2
2
 R= D ; ∆ =
R ∆D
2 2
1
 Keliling =
∑ Keliling ; ∆Keliling =
1 n ∑ i2 − (∑ i ) 2

kel kel 2

5 n  n −1 
 
2 2
Keliling ∂r 2 1 2
 r= ; ∆r 2 = ∆keliling = ∆keliling
2π ∂kel 2π
α+ +α −
 α= ;
2
∂α ∂α 1 1
α
∆ = ∆α + + ∆α − = ∆α + + ∆α−
∂α + ∂α − 2 2
360 0 L ⋅ m ⋅ g ⋅ r
 G= ;
π 2 R 4α 0
2 2 2 2 2
∂G 2 ∂G 2 ∂G 2 360 0 L ⋅ m ⋅ g 2
∆ 2 =
G ∆r + ∆R + ∆α = ∆r +
∂r 3 ∂R ∂α π2R4α
2 2 2
4 ⋅ 360 0 L ⋅ m ⋅ g ⋅ r 2 360 0 L ⋅ m ⋅ g ⋅ r 2 360 0 ⋅ m ⋅ g ⋅ r 2
∆R + ∆α + ∆L
π 2 R5α π 2 R 4α 2 π 2 R 4α
2
360 0 ⋅ L ⋅ g ⋅ r
, dimana ∆L dan ∆m adalah 0.
2
+ ∆m
π 2 R 4α
 G=
∑G ; ∆G =
∑∆G untuk setiap L
5 5
Cara Grafik :
α(0)

∆α
tan θ = ; ∆ tan θ
θ ∆m
360 0 L ⋅ g ⋅ r
m (gr) G=
π 2 R 4 tan θ

10. 2 2 2 2
∂G 2 ∂G 2 ∂G 2
∆G = ∆r + ∆R + ∆tan θ
∂r 3 ∂R ∂ tan θ
2 2 2 2 2
360 0 L ⋅ g 2 4 ⋅ 360 0 L ⋅ g ⋅ r 2 360 0 L ⋅ g ⋅ r 2
= ∆r + ∆R + ∆ tan θ
π 2 R 4 tan θ 3 π 2 R 5 tan θ π 2 R 4 tan 2 θ 3
Ambil 3 dari 6 L sebagai sample
α(0)

∆α
tan θ = ; ∆ tan θ
θ ∆L
360 0 ⋅ g ⋅ r ⋅ m
L (cm) G=
π 2 R 4 tan θ
2 2 2 2
∂G 2 ∂G 2 ∂G 2
∆G = ∆r + ∆R + ∆tan θ
∂r 3 ∂R ∂ tan θ
2 2 2 2 2
360 0 m ⋅ g 2 4 ⋅ 360 0 m ⋅ g ⋅ r 2 360 0 ⋅ M ⋅ g ⋅ r 2
= ∆r + ∆R + ∆ tan θ
π 2 R 4 tan θ 3 π 2 R 5 tan θ π 2 R 4 tan 2 θ 3
Ambil 3 dari 5 m sebagai sample
Perhitungan :
3,63 + 3,53 + 3,64 + 3,53 + 3,43 + 3,43 + 3,53 + 3,43 + 3,53 + 3,53
 D =
10
=3,521 mm = 0,3521 cm
1
1 0,5159  2
∆ =
D = 0,02394 mm = 0,002394
10  10 −1 
 
Angka Pelaporan ( 3,521 ± 0,024 ) 10-1 cm
1
 R= × 0,3521 = 0,17605 cm
2
2
1 2
∆ =
R 0,002394 = 0,000001433 cm
2
Angka Pelaporan ( 1,176050 ± 0,0000014 ) 10-1 cm

11. 30 + 30,5 + 31 + 31 + 30
 Keliling = = 30,5 cm
5
1
1 5 ⋅ 4652,25 − 23256,25  2
∆Keliling =  = 0,2236
cm
5 5 −1 
Angka Pelaporan ( 3,050 ± 0,022 ) 10-1 cm
30,5
 r= = 4,8542 cm
2π
2
1 2
∆r = 0,2236 = 0,0012664 cm
2π
Angka Pelaporan ( 4,8542 ± 0,0013 ) cm
 Menghitung α dan ∆α
L(cm) Percobaan 1 Percobaan 2 Percobaan 3
L1 = 10 L2 = 20 L1 = 30 L2 = 40 L1 = 50 L2 = 60
α( )
o
α( ) o
α( ) o
α( ) α
o
α( )
o
α (o )
m (gr)
0,5
(1,0±0,5) (4,0±0,5) (2,0±0,5) (3,0±0,5) (3,0±0,5) (6,0±0,5)
1 (1,0±0,5) (5,0±0,5) (4,0±0,5) (5,0±0,5) (5,0±0,5) (8,0±0,5)
1,5 (2,0±0,5) (7,0±0,5) (6,0±0,5) (7,0±0,5) (7,0±0,5) (1,00±0,05)10
2
(5,0±0,5) (9,0±0,5) (8,0±0,5) (9,0±0,5) (9,0±0,5) (1,20±0,05)10
2,5 (6,0±0,5) (1,10±0,05)10 (1,00±0,05)10 (1,20±0,05)10 (1,10±0,05)10 (1,40±0,05)10
 Menghitung G dan ∆ G
L (cm) Percobaan 1
L1 = 10 L2 = 20
G ( x 1011 dyne / cm2 ) G ( x 1011 dyne / cm2 )
m (gr)
0,5 ( 9,22 ± 0,21 ) 10-2 (4,61 ± 0,33) 10-2
1 ( 1,84 ± 0,09 ) 10-1 (7,9 ± 0,5) 10-2
1,5 ( 1,382 ± 0,012 ) 10-1 (7,90 ± 0,32) 10-2
2 (7,37 ± 0,5) 10-2 (8,19 ± 0,21) 10-2
2,5 (7,68 ± 0,4) 10-2 (8,38 ± 0,15) 10-2
L (cm) Percobaan 2
L1 = 30 L2 = 40
G ( x 1011 dyne / cm2 ) G ( x 1011 dyne / cm2 )
m (gr)

12. 0,5 (1,382 ± 0,012) 10-1 (1,23 ± 0,04) 10-1
1 (1,382 ± 0,030) 10-1 (1,475 ± 0,022) 10-1
1,5 (1,382 ± 0,013) 10-1 (1,580 ± 0,013) 10-1
2 (1,38 ± 0,07) 10-1 (1,64 ± 0,08) 10-1
2,5 (1,382 ± 0,05) 10-1 (1,54 ± 0,04) 10-1
L (cm) Percobaan 3
L1 = 50 L2 = 60
G ( x 1011 dyne / cm2 ) G ( x 1011 dyne / cm2 )
m (gr)
0,5 (1,54 ± 0,07) 10-1 (9,2 ± 0,6) 10-2
1 (1,843 ± 0,034) 10-1 (1,38 ± 0,08) 10-1
1,5 (1,975 ± 0,020) 10-1 (1,66 ± 0,07) 10-1
2 (2,048 ± 0,013) 10-1 (1,84 ± 0,06) 10-1
2,5 (2,10 ± 0,09) 10-1 (1,98 ± 0,05) 10-1
 Menghitung G dan ∆G
Percobaan L ( cm ) G ( x 1011 dyne / cm2 )
L1 = 10 ( 1,13 ± 0,04 ) 10-1
L2 = 20 ( 7,39 ± 0,030 ) 10-2
1
L1 = 30 ( 1,382 ± 0,035 ) 10-1
L2 = 40 ( 1,493 ± 0,039 ) 10-1
2
L1 = 50 ( 1,90 ± 0,05 ) 10-1
L2 = 60 ( 1,56 ± 0,06 ) 10-1
3
G ( 1,367 ± 0,010 ) 10-1
Cara Grafik :
1. Grafik simpangan α terhadap massa ( m )
 Grafik simpangan α terhadap massa ( m ) pada L = 10 cm

13. 0,5 + 1 + 1,5 + 2 + 1,5
X = = 1,5 gr
5
1+1+ 2 + 5 + 6
Y= = 3 derajat
5
Titik sentroid : ( X, Y ) = ( 1,5 , 3 )
∆α 5,1 − 4,2
tan θ = = =3
∆m 2,2 −1,9
∆α 5,6 − 4,6
tan θ1 = = = 6,67
∆m 1,9 −1,75
∆α 3,8 − 3,6
tan θ2 = = = 0,57
∆m 2,4 − 2,05
∆θ1 = tan θ − tan θ1 = 3 − 6,67 = 3,37
∆θ2 = tan θ − tan θ2 = 3 − 0,57 = 2,43
3,37 + 2,43
∆θ = = 2,9
2
Angka pelaporan : ( 3,0 ± 2,9 )

14. 360 0 L ⋅ g ⋅ r 360 ⋅ 10 ⋅1000 ⋅ 48,542
G= = = 6258602565 = 0,625 x 1011 dyne/cm2
π 2 R 4 tan θ 9,689 ⋅ 0,0009609 ⋅ 3
2 2 2
360 ⋅10 ⋅1000 2 4 ⋅ 360 ⋅10 ⋅1000 ⋅ 48,542 2
∆ =
G ⋅ 0,00127 + 0,00000143
9,689 ⋅ 0,0009609 ⋅ 3 3 9,689 ⋅ 0,000169 ⋅ 3
2 2
360 ⋅10 ⋅1000 ⋅ 48,542 2
+ ⋅ 2,9 = 1,190894 ⋅1010 + 3,140555 ⋅1010 +1,62 ⋅1010
9,689 ⋅ 0,0009609 ⋅ 9 3
= 0,595 ⋅1011 dyne/cm2
Angka pelaporan : ( 6,3 ± 6,0 ) 10-1 ( x 1011 dyne/cm2 )
 Grafik simpangan α terhadap massa ( m ) pada L = 20 cm

15. 0,5 + 1 + 1,5 + 2 + 1,5
X = = 1,5 gr
5
4 + 5 + 7 + 9 + 11
Y= = 7,2 derajat
5
Titik sentroid : ( X, Y ) = ( 1,5 , 7,2 )
∆α 5,2 − 4,2
tan θ = = = 3,57
∆m 0,9 − 0,62
∆α 11 −10,4
tan θ1 = = = 4,286
∆m 2,1 −1,96
∆α 8,8 − 8,0
tan θ2 = = = 1,74
∆m 2,4 −1,94
∆ 1 = tan θ − tan θ1 = 3,57 − 4,286 = 0,716
θ
∆ 2 = tan θ − tan θ2 = 3,57 −1,74 =1,83
θ
0,716 +1,83
θ
∆ = =1,273
2
Angka pelaporan : ( 3,57 ± 1,27 )
360 0 L ⋅ g ⋅ r 360 ⋅ 10 ⋅ 1000 ⋅ 48,542
G= = = 5257687885 = 0,526 x1011 dyne/cm2
π R tan θ
2 4
9,689 ⋅ 0,0009609 ⋅ 3,57
2 2 2
360 ⋅10 ⋅1000 2 4 ⋅ 360 ⋅10 ⋅1000 ⋅ 48,542 2
∆ =
G ⋅ 0,00127 + 0,00000143
9,689 ⋅ 0,0009609 ⋅ 3,57 3 9,689 ⋅ 0,000169 ⋅ 3,57
2 2
360 ⋅10 ⋅1000 ⋅ 48,542 2
+ ⋅1,27 = 1,4097 ⋅1010 + 2,224 ⋅1010 +1,42 ⋅1010
9,689 ⋅ 0,0009609 ⋅12,7 3
= 0,505 ⋅1011 dyne/cm2
Angka pelaporan : ( 5,3 ± 5,1 ) 10-1 ( x 1011 dyne/cm2 )
 Grafik simpangan α terhadap massa ( m ) pada L = 30 cm

16. 0,5 + 1 + 1,5 + 2 + 1,5
X = = 1,5 gr
5
2 + 4 + 6 + 8 + 10
Y= = 6 derajat
5
Titik sentroid : ( X, Y ) = ( 1,5 , 6 )
∆α 8,8 − 7,4
tan θ = = = 2,54
∆m 2,4 −1,85
∆θ = 0
Angka pelaporan : ( 2,5 ± 0,0 )
360 0 L ⋅ g ⋅ r 360 ⋅10 ⋅ 1000 ⋅ 48,542
G= = = 7389742421 = 0,73 x 1011 dyne/cm2
π R tan θ
2 4
9,689 ⋅ 0,0009609 ⋅ 2,54
2 2 2
360 ⋅10 ⋅1000 2 4 ⋅ 360 ⋅10 ⋅1000 ⋅ 48,542 2
∆ =
G ⋅ 0,00127 + 0,00000143
9,689 ⋅ 0,0009609 ⋅ 2,54 3 9,689 ⋅ 0,000169 ⋅ 2,54
2 2
360 ⋅10 ⋅1000 ⋅ 48,542 2
+ ⋅0 = 1,66 ⋅1010 + 3,77 ⋅1010 + 0
9,689 ⋅ 0,0009609 ⋅ 6,45 3

17. = 0,543 ⋅1011 dyne/cm2
Angka pelaporan : ( 7,3 ± 5,4 ) 10-1 ( x 1011 dyne/cm2 )
0,63 + 0,53 + 0,73
G= = 0,63 ( x 1011 dyne/cm2 )
3
0,6 + 0,51 + 0,54
∆G = = 0,55 ( x 1011 dyne/cm2 )
3
Angka pelaporan : ( 6,3 ± 5,5 ) 10-1 ( x 1011 dyne/cm2 )
2. Grafik simpangan α terhadap panjang batang ( L )
 Grafik simpangan α terhadap panjang batang ( L ) pada m = 0,5 gr

18. 10 + 20 + 30 + 40 + 50 + 60
X = = 35 gr
6
1+ 4 + 2 + 2 + 3 + 6
Y= = 3 derajat
6
Titik sentroid : ( X, Y ) = ( 35, 3 )
∆α 4,8 − 4,2
tan θ = = = 0,12
∆m 50 − 45
∆α 6,2 − 4,8
tan θ1 = = = 0,15
∆m 44 − 40
∆α 3,8 − 3,4
tan θ 2 = = = 0,033
∆m 60 − 48
∆ 1 = tan θ − tan θ1 = 0,12 − 0,15 = 0,03
θ
∆θ2 = tan θ − tan θ2 = 0,12 − 0,033 = 0,087
0,03 + 0,087
∆θ = = 0,0585
2
Angka pelaporan : ( 1,2 ± 0,6 ) 10-1
360 0 m ⋅ g ⋅ r 360 ⋅ 0,5 ⋅1000 ⋅ 48,542
G= = = 0,782 x1011 dyne/cm2
π 2 R 4 tan θ 9,689 ⋅ 0,0009609 ⋅ 0,12
2 2 2
360 ⋅ 0,5 ⋅1000 2 4 ⋅ 360 ⋅ 0,5 ⋅1000 ⋅ 48,542 2
∆ =
G ⋅ 0,00127 + 0,00000143
9,689 ⋅ 0,0009609 ⋅ 0,12 3 9,689 ⋅ 0,000169 ⋅ 0,12
2 2
360 ⋅ 0,5 ⋅1000 ⋅ 48,542 2
+ ⋅ 0,0585 = 1,86 ⋅1010 + 2,47 ⋅1010 + 2,46 ⋅1010
9,689 ⋅ 0,0009609 ⋅ 0,0144 3
= 0,679 ⋅1011 dyne/cm2
Angka pelaporan : ( 7,8 ± 6,8 ) 10-1 ( x 1011 dyne/cm2 )
 Grafik simpangan α terhadap panjang batang ( L ) pada m = 1 gr

19. 10 + 20 + 30 + 40 + 50 + 60
X = = 35 gr
6
1+ 5 + 4 + 5 + 5 + 8
Y= = 4,67 derajat
6
Titik sentroid : ( X, Y ) = ( 35, 4,67 )
∆α 8,2 − 7,4
tan θ = = = 0,12
∆m 55 − 50
∆α 8,0 − 7,2
tan θ1 = = = 0,2
∆m 46 − 42
∆α 6,0 − 5,6
tan θ 2 = = = 0,04
∆m 58 − 48
∆ 1 = tan θ − tan θ1 = 0,12 − 0,2 = 0,08
θ
∆ 2 = tan θ − tan θ2 = 0,12 − 0,04 = 0,08
θ
0,08 + 0,08
∆θ = = 0,08
2
Angka pelaporan : ( 1,2 ± 0,8 ) 10-1
360 0 m ⋅ g ⋅ r 360 ⋅1 ⋅1000 ⋅ 48,542
G= = = 0,156 x1011 dyne/cm2
π R tan θ
2 4
9,689 ⋅ 0,0009609 ⋅ 0,12

20. 2 2 2
360 ⋅1 ⋅1000 2 4 ⋅ 360 ⋅1 ⋅1000 ⋅ 48,542 2
∆ =
G ⋅ 0,00127 + 0,00000143
9,689 ⋅ 0,0009609 ⋅ 0,12 3 9,689 ⋅ 0,000169 ⋅ 0,12
2 2
360 ⋅1 ⋅1000 ⋅ 48,542 2
+ ⋅ 0,08 = 0,144 ⋅1010 + 0,759 ⋅1010 + 0,203 ⋅1010
9,689 ⋅ 0,0009609 ⋅ 0,0144 3
= 0,111 ⋅1011 dyne/cm2
Angka pelaporan : ( 1,56 ± 1,11 ) 10-1 ( x 1011 dyne/cm2 )
0,78 + 0,156
G= = 0,468 ( x 1011 dyne/cm2 )
2
0,68 + 0,11
∆G = = 0,395 ( x 1011 dyne/cm2 )
3
Angka pelaporan : ( 4,7 ± 4,0 ) 10-1 ( x 1011 dyne/cm2 )
VII. TUGAS AKHIR
1. Buatlah grafik hubungan antara α dengan m untuk tiap harga L tertentu
(ambil α˚ = 0 untuk m = 0)
2. Buatlah grafik hubungan antara α˚ dengan L9m) untuk tiap harga m
tertentu.
3. Sesuaikan hasil diatas dengan gambar grafik dan rumus
4. Hitunglah harga m/ α˚ untuk tiap L dari grafik α˚ terhadap m kemudian
hitung harga G untuk tiap harga L secara grafis, lalu ambil rata-ratanya.
5. Hitung harga L/ α˚ untuk tiap m secara grafis (L terhadap α˚), kemudian
hitung harga G untuk tiap m secara grafis, lalu ambil rata-ratanya.
6. Bahan apaqkah yang diukur tersebut? Berdasarkan apakah peryataan itu
dikemukakan (sebut sumber litelatur/table-tabel).
7. Apakah pada saat pembebanan, batang yang diukur boleh melengkung?
Jelaskan!
8. Tentukan dengan cara yang sama, harga G untuk batang logam yang lain.
9. Berdasarkan pertanyaan 8, bahan apakah yang diselidiki?
Jawaban :

21. 1. Telah dibuat di pengolahan data.
2. Telah dibuat di pengolahan data.
3. Telah dibuat di pengolahan data.
4. Telah dibuat di pengolahan data.
5. Telah dibuat di pengolahan data.
6. Bahan yang dipakai adalah . Hal ini dapat terbukti dengan melihat nilai G
atau modulus punter batang tersebut dan mencocokannya dengtan tabel
yang terdapat di laboratorium fisika dasar.
7. Saat pembebanan, batang tidak boleh melengkung karena salah satu syarat
dari percobaan ini adalah batang yang dipakai harus sama partikelnya.
Sedangkan kalau batang melelngkung, batang tersebut tidak sama
partikelnya.
8. Pada percobaan ini hanya digunakan satu buah batang logam.
9. Pada percobaan ini hanya digunakan satu buah batang logam.
VIII. ANALISA
Setelah melakukan percobaan ini terdapat beberapa hal yang perlu
dianalisa yaitu sebagai berikut :
Setelah didapat hasil dari pengolahan data, saya membandingkan hasil
yang didapat dari rumus dan hasil yang didapat dari kedua grafik. Berikut
hasilnya :
G dari rumus :
( 1,367 ± 0,010 ) 10-1 ( x 1011 dyne / cm2 )
G dari grafik simpangan α terhadap massa ( m ) :
( 6,3 ± 5,5 ) 10-1 ( x 1011 dyne/cm2 )
G dari grafik simpangan α terhadap panjang batang ( L ) :
( 1,56 ± 1,11 ) 10-1 ( x 1011 dyne/cm2 )
Terlihat dari hasil di atas ternyata G yang diperoleh berbeda. Hal ini
mungikn disebabkan oleh :

22.  Kesalahan ketika melihat simpangan pada busur yang mempengaruhi data
pengamatan.
 Kesalahan pada pemasangan jarum yang seharusnya berada di tengah.
 Kesalahan ketika melakukan perhitungan sehingga didapat G yang
berbeda.
 Kesalahan dalam pembuatan grafik.
IX. KESIMPULAN
Setelah melakukan percobaan ini maka dapat diambil beberapa
kesimpulan yaitu diantaranya :
1. Modulus Geser atau adalah bilangan yag menggambarkan perubahan
benda yang elastis, atau suatu konstanta yang menyatakan besarnya gaya
yang diperlukan untuk memuntir suatu bahan per satuan luar tiap satu
derajat. Pada percobaan ini terlihat pada saat batang tambahkan beban
maka logam akan memuntir dan pada saat dikurangi beban maka batang
tidak akan langsung kembali ke posisi awal, karena batang tersebut
mempunyai daya elastisitas sehingga saat dibebani partikel – partikel pada
batang tersebut bertambah.
2. Puntiran diteruskan ke arah memanjang maksudnya adalah bahwa di
semua tempat di sepanjang batang mengalami puntiran. Hal ini
disebabkan karena setiap batang memiliki daya elastisitasnya masing –
masing. Semakin mendekati beban maka daya puntiran batang akan
semakin besar. Hal ini ditandai dengan simpangan pada busur derajat akan
semakin besar bila mendekati beban.
3.

23. Gambar diatas menunjukan grafik hubungan antara besar simpangan
dengan massa beban yang ditambahkan. Dari grafik dapat terlihat bahwa
semakin banyak beban yang akan ditambahkan maka simpangan pada
busurpun akan semakin besar. Hal ini terjadi di setiap titik pada batang
tersebut. Hal ini seperti telah diulas di atas terjadi karena adanya daya
elastisitas pada batang logam. Semua logam memiliki daya elastisitasnya
masing – masing. Daya elastisitas setiap logam berbeda – beda. Apabila
beban terus ditambahkan maka grafik akan mendekati batas elastisitas
batang yang dapat didefinisikan batas dimana suatu batang logam telah
mencapai daya elastisitasnya yang maksimum. Setelah ditambahkan beban
kembali maka batang akan mencapai titik patah yang menyebabkan
batang logam akan patah.
X. DAFTAR PUSTAKA
Team. 2004. Modul Praktikum Fisika Dasar. Bandung : Laboratorium Fisika
Dasar – ITENAS.
Tyler. F. ” A laboratory of Physics ”. Edward Arnold 1967.