Percobaan ini bertujuan untuk mempelajari karakteristik aliran fluida tak mampu mampat dalam sistem perpipaan dengan menggunakan orificemeter dan menentukan faktor-faktor seperti koefisien orificemeter, hilang tekanan akibat gesekan, panjang ekivalen perlengkapan pipa, dan karakteristik pompa. Prosedur percobaan meliputi peneraan orificemeter, pengukuran laju alir, dan penentuan bilangan Reynold,

1. BAB I
PENDAHULUAN
1.1 Latar Belakang
Perilaku fluida merupakan hal yang penting dalam teknik proses pada
umumnya dan merupakan salah satu dasar yang diperlukan untuk mempelajari satuan-
satuan proses. Proses-proses di industri kimia acap kali memerlukan pengaliran fluida
melalui pipa, saluran dan peralatan proses. Para sarjana kimia biasanya berhadapan
dengan masalah aliran didalam pipa tertutup yang penuh dengan fluida bergerak. Tetapi
mereka juga sering menemukan masalah dimana fluida yang mengalir dalam pipa tidak
terisi penuh.
Di industri kimia, penggunaan energi sangat penting. Sedangkan didalam
suatu sistem perpipaan, pada proses perpindahan massa terdapat energi yang hilang dari
fluida.
1.2 Tujuan Percobaan
Percobaan ini bertujuan untuk :
1.2.1 Dapat melakukan peneraan orificemeter.
1.2.2 Dapat menentukan koefisien orificemeter (Co).
1.2.3 Dapat menentukan friction losses pada sistem perpipaan (Ғ)
1.2.4 Dapat menentukan panjang ekivalen dari perangkat perlengkapan sistem
perpipaan (Le).
1.2.5 Dapat menentukan karekteristik pompa.

2. 1.3 Ruang Lingkup
Fluida terbagi menjadi dua, yaitu: fluida cair dan fluida gas. Berdasarkan
pengaruh tekanan dan temperatur terhadap densitas, fluida dibagi menjadi dua:
1. Fluida incompressible (tak mampu mampat)
Adalah fluida yang jika tekanan dan suhunya berubah maka akan mengakibatkan
ketidakberubahan densitas fluida secara signifikan.
Contoh: zat cair ( air,larutan)
2. Fluida compressible (mampu mampat)
Adalah fluida yang jika temperature dan tekanan berubah sedikit saja maka akan
mengakibatkan perubahan densitas fluida secara signifikan.
Contoh: gas
Dalam percobaan ini yang akan digunakan adalah fluida incompressible (tak
mampu mampat) yaitu air dalam suatu sistem perpipaan yang digunakan untuk
mempelajari energi yang hilang akibat adanya faktor gesekan dan adanya bagian-bagian
dari perlengkapan pipa. Dimana pada sistem perpipaan tersebut tidak terdapat konsumsi
dan regenerasi yang dilakukan oleh fluida (air). Selain itu kondisi yang terjadi
diasumsikan steady state dan tidak melibatkan alat penukar panas.

3. BAB II
TINJAUAN PUSTAKA
Fluida merupakan zat yang mampu mengalir dan menyesuaikan diri dengan
bentuk tempatnya. Pada suhu dan tekanan tertentu, setiap fluida mempunyai densitas
atau rapat massa tertentu. Walaupun densitas fluida bergantung pada suhu dan tekanan,
perubahan densitas karena perubahan variable itu mungkin besar dan mungkin kecil.
Jika densitas itu hanya sedikit terpengaruh oleh perubahan yang agak besar pada suhu
dan tekanan tertentu, maka fluida tersebut disebut fluida tak mampu mampat
(incompressible). Tetapi apabila densitasnya peka terhadap perubahan variable tekanan
dan temperature disebut fluida mampu mampat (compressible). Zat cair biasanya
dianggap fluida tak mampu mampat. Sedangkan gas merupakan fluida mampu mampat.
Untuk mempelajari karakteristik aliran fluida tak mampu mampat dalam
sistem perpipaan, yang meliputi pipa beserta alat perlengkapannya berlaku hukum
Bernoulli.Persamaan Bernoulli ini diturunkan dari persamaan neraca energi yaitu:
d [m( u + g.z +
2
2
v
)]sys = ( U + ρ
P
+ g.z +
2
2
v
)in dmin – ( U + ρ
P
+ g.z +
2
2
v
)out dmout +
dQ – dw
dengan asumsi bahwa sistem dalam keadaan steady state, maka nilai akumulasi = 0
maka persamaannya menjadi:
( U + ρ
P
+ g.z +
2
2v
)in dmin – ( U + ρ
P
+ g.z +
2
2
v
)out dmout = dQ – dW
kedua ruas dibagi aliran massa
( U + ρ
P
+ g.z +
2
2
v
)in – ( U + ρ
P
+ g.z +
2
2
v
)out = dQ/dm – dW/dm
input – output = akumulasi
ρ
P∆
+ g. z∆ +
2
2
v∆
= - W – ( U∆ –Q )
Karena fluida yang digunakan adalah fluida yang incompresible liqiud maka

4. U∆ – Q = Ғ,
sehingga persamaan diatas menjadi:
( ρ
P∆
+ g. z∆ +
2
2
v∆
) = -W – Ғ ( Persamaan Bernoulli )
2.1 Pengukuran laju alir
Untuk mengukur laju alir fluida di dalam pipa digunakan orificemeter.
Orificemeter adalah alat untuk mengukur laju alir fluida didalam pipa. Persamaan baku
orificemeter dapat diturunkan dari persamaan Bernoulli.
( ρ
P∆
+ g. z∆ +
2
2
v∆
) = -W – Ғ
Dengan menggunakan asumsi :
1. z∆ diabaikan karena pada sistem yang ditinjau yaitu orifice ketinggian aliran
masuk sama dengan tinggi aliran keluar.
2. W dapat diabaikan karena sistem yang ditinjau adalah orificemeter, dimana pada
sistem tersebut tidak terdapat pompa.
3. F dapat diabaikan karena diasumsikan fluida adalah fluida ideal dimana tidak
terjadi gaya tarik menarik dengan dinding orificemeter.
Sehingga persamaan Bernoulli diatas menjadi :
ρ
P∆
-
2
2
v∆
= 0
P∆ = P2–P1 v2
= v2
2
– v1
2
Maka di dapat persamaan :
ρ
12 PP −
+
2
2
1
2
2 vv −
= 0 ……………………….(1)
Dari neraca massa :

5. (laju alir massa masuk)–(laju alir massa keluar)+(konsumsi)–(regenerasi)= (akumulasi)
min – mout + konsumsi – regenerasi = akumulasi
karena tidak ada reaksi kimia yang terjadi maka konsumsi dan regenerasi dapat
diabaikan atau nilainya mendekati nol. Sedangkan untuk akumulasi karena sisitem
diasumsikan steady state maka akumulasi dapat diabaikan atau sama dengan nol.
Dari asumsi diatas maka diperoleh:
inm – outm = 0
inm = outm
laju alir massa (m) sendiri merupakan hasil perkalian antara densitas(ρ) fluida dengan
debit (Q)
inm = outm
ρ1.Q1 = ρ2.Q2
ρ1.A1.v1 = ρ2.A2.v2
karena fluida yang digunakan adalah fluida tak mampu mampat maka ρ1 = ρ2
A1.v1 = A2 .v2 ( persamaan kontinuitas )
v1 =
1
2
A
A
* v2 …………………………………..(2)
persamaan (1) dan (2)
ρ
12 PP −
=
2
2
2
2
1 vv −
ρ
12 PP −
=
2
)*( 2
2
2
2
1
2
vv
A
A
−
ρ
12 PP −
=
2
)(* 2
2
1
22
2 v
A
A
v −
ρ
12 PP −
=
2
)1)(( 2
1
22
2 −
A
A
v
2
2v =
]1)[(
)(2
2
1
2
12
−
−
A
A
PP
ρ
2v =
])(1[
)(2
2
1
2
21
A
A
PP
−
−
ρ

6. Dengan asumsi yang digunakan untuk merumuskan kecepatan fluida dimana tidak
terdapat beda ketinggian (∆Z = 0) dan tidak ada kerja yang digunakan (W = 0), maka
perlu digunakan factor koreksi ( Co )
2v = Co .
])(1[
)(2
2
1
2
21
A
A
PP
−
−
ρ
Q ≅ A2.v2
Q = Co.A2.
])(1[
)(2
2
1
2
21
A
A
PP
−
−
ρ
Q = Co.A2.
])(1[
2
2
1
2
A
A
−ρ 21 PP −
Harga Co.A2.
])(1[
2
2
1
2
A
A
−ρ
tetap, maka dimisalkan sebagai k sehingga dapat ditulis
Q = k 21 PP − dimana 21 PP − = manometerh∆
Maka untuk kalibrasi orificemeter dapat dilakukan dengan membuat grafik Q terhadap
h∆
Q
h∆
Slope dari grafik diatas adalah harga nilai dari konstanta k. apabila harga k di ketahui
maka kita dapat menentukan harga factor koreksi (Co)
2.2 Bilangan Reynold
Bilangan Reynold (NRe) adalah suatu bilangan tanpa dimensi yang berlaku
pada saat zat alir dengan viskositas μ dan densitas ρ yang mengalir dengan laju v
melalui suatu pipa ( atau melalui suatu rintangan ) dengan diameter D
NRe = µ
ρ Dv **
Pada sistem perpipaan tertutup baik untuk aliran laminer maupun aliran turbulen
memiliki harga NRe = 10.000 dengan syarat alirannya stedi state dan berkembang
penuh (McCabe, Smith dan Harriot, Operasi Teknik Kimia jilid 1).

7. 2.3 Faktor Gesekan
Apabila di dalam aliran fluida terdapat gaya gesekan dengan pipa maka dapat
digunakan persamaan fanning :
)5(....
.2
.)(
)4(....
..2
2
2
air
cairHg
LV
Dhg
LV
DF
f
ρ
ρρ ∆−
=
=
Dimana Ғ : Hilang tekan karena gesekan (N/m2
)
ƒ : factor gesekan
v : kecepatan rata-rata fluida (m/s)
l : panjang pipa (m)
ρ : densitas fluida (kg/m3
)
D: diameter pipa (m)
gc: 1 (tetapan konvensional) (kg.m/N.s2
)
Persamaan fanning berlaku tergantung pada jenis kekasaran pipa dan jenis
aliran. Besarnya gaya gesek didalam pipa dapat dihitung juga dengan persamaan
Bernoulli. Adapun asumsi yang digunakan adalah sebagai berikut :
1. Kecepatan di sepanjang pipa tetap
2. Tidak terdapat perbedaan ketinggian.
3. Tidak ada kerja masuk.
F
PP
FW
V
Zg
P
=
−
−−=
∆
+∆+
∆
ρ
ρ
12
2
2
2.4 Panjang Ekivalen
Panjang ekivalen adalah panjang pipa lurus yang dapat digunakan untuk
menggantikan sambungan (misal : valve, elbow, sambungan T, dll) dimana pada laju
alir yang sama memberikan pressure drop atau friction losses yang sama.

8. Ғ =
D
vlf e
2
...2
……….. (1)
ρ
P∆
= - Ғ ………………(2)
persamaan (1) dan (2) :
ρ
12 PP −
=
D
vlf e
2
...2
el =
ρ
12 PP −
2
..2 vf
D
Dalam penentuan factor fanning dapat dilakukan dengan menggunakan 3 cara yaitu:
1. Dengan menggunakan grafik NRe terhadap factor gesekan Ғ . Apabila
menggunakan grafik maka ada data yang diperlukan yaitu tingkat kekerasan pipa
harus diketahui.

9. 2. Menggunakan persamaan rumus empirik yaitu factor fanning fungsi dari
bilangan Reynold ƒ = φ (NRe)
Untuk aliran laminar : NRe < 2000
Re
16
N
f =
untuk aliran turbulen : NRe > 4100
25,0
Re
079,0
N
f =
3. Menggunakan data-data percobaan
2.5 Pompa
Pompa digunakan dalam sistem aliran untuk meningkatkan energi mekanik
fluida yang mengalir. Peningkatan itu digunakan untuk mempertahankan aliran. Energi
mekanik yang diberikan pompa harus dikurangi dengan rugi gesekan. Tetapi pada
prakteknya digunakan efisiensi pompa. Untuk mengetahui kerja pompa yang diberikan
pada sistem maka kita dapat menggunakan persamaan Bernoulli dengan menggunakan
asumsi yaitu:
1. Kecepatan di sepanjang pipa sama ( v∆ =0)
2. Factor gesekan pompa diabaikan
3. Tidak terdapat perbedaan ketinggian ( z∆ =0)
Maka persamaan Bernoulli :
ρ
P∆
= - W
Karakteristik pompa dapat ditentukan berdasarkan:
1. Kerja Pompa (W) :

10. air
airHg hg
W
W
PP
ρ
ρρ
ρ
∆−
=
−=
−
)(
12
2. Head pompa (H)
air
airHg
g
hg
H
g
W
H
ρ
ρρ
.
)( ∆−
=
=
3. Daya pompa ( P )
WmP .=
( ) QhgP
Q
P
P
airHgf ..∆−=





∆
=
ρρ
ρ
ρ
4. Efisiensi pompa ( η )
%100x
P
P
act
=η
P = Daya teoritis yang didapat dari persamaan bernoulli
P act = Daya poros yang disuplai oleh pompa
BAB III
METODOLOGI PERCOBAAN

11. 3.1 Alat dan Bahan
1. Alat
• Pipa, tangki, pompa 1 buah
• Orificemeter 1 buah
• Manometer pipa U 2 buah
• Viskometer 1 buah
• Piknometer 1 buah
• Stopwatch 1 buah
• Gelas ukur 1000 ml 1 buah
2. Bahan
• Aquadest
• Air kran
3.2 Prosedur Kerja

12. 1. Peneraan Orificemeter
Mengisi tangki dengan air hingga ketinggian tertentu
Mengalirkan air dari tangki dengan bantuan pompa ke pipa yang telah di
pasang orificemeter kemudian ukur perbedaan ketingguan manometer
Mengukur waktu yang diperlukan air untuk mencapai volume tertentu
Mengukur t dan V untuk perbedaan manometer yang lain
2. Penentuan faktor gesekan pipa
Mengisi tangki dengan air kran sampai ketinggian tertentu
Menentukan volum control yang akan digunakan pada sistem
Memasang manometer pada pipa yang akan ditentukan factor
gesekannya
Mengalirkan air pada pipa yang sudah ditentukan dengan bantuan
pompa secara recycle
Mencatat h∆ pada manometer yang dipasang pada orificemeter
dan pipa
3. Penentuan panjang ekivalen
Menentukan volum control yang akan digunakan sebagai sistem
Memasang manometer pada perlengkapan pipa yang akan diukur

13. panjang ekivalennya
Mengalirkan air pada system yang telah ditentukan dengan bantuan
pompa secara recycle
Mencatat h∆ manometer yang dipasang pada perlengkapan pipa dan
orificemeter
4. Efesiensi pompa
Menentukan volum control yang akan digunakan sebagai sisitem
Mengalirkan air pada pipa
Mencatat h∆ pada orificemeter, serta waktu alir
3.3 Skema Alat

14. BAB IV
HASIL PERCOBAAN
4.1 Kurva Kalibrasi Orificemeter

15. Kalibrasi Orificemeter
y = 0.0014x
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.05 0.1 0.15 0.2 0.25 0.3
Ah (m)
Q(m3/s)
4.2 Kurva hubungan Q (m3
/s) terhadap Co (Faktor koreksi orifice)
Grafik Q (m3/s) terhadap Co
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
Co
Q(m3/s)
4.3 Kurva Karakteristik Pompa
Kurva karakteristik pompa
y = 3E-05x + 0.0001
R2
= 0.9847
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 1 2 3 4 5 6 7 8 9 10
W
Q(m3/s)

16. Kurva hubungan Q (m3/s) terhadap n (efisiensi)
y = 9263.4x - 1.3521
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
0 0.00005 0.0001 0.00015 0.0002 0.00025 0.0003 0.00035 0.0004
Q (m3/s)
n
Kurva hubungan Q (m3/s) terhadap H (Head total)
y = 0.0003x + 0.0001
R2
= 0.9847
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
H
Q(m3/s)
4.4 Kurva hubungan Q (m3
/s) terhadap F (friction losses)
Kurva hubungan Q (m3/s) terhadap F (friction Losses)
pada pipa D 1.25 in
y = 0.0004x + 0.0001
R2
= 0.9162
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
F
Q(m3/s)
Kurva hubungan Q (m3/s) terhadap F (friction Losses)
pada pipa D 1 in
y = 0.0004x + 0.0001
R2
= 0.9803
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
F
Q(m3/s)

17. Kurva hubungan Q (m3/s) terhadap F (friction Losses)
pada pipa D 0.75 in
y = 0.0003x + 7E-05
R2
= 0.9842
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
F
Q(m3/s)
4.5 Kurva hubungan Q (m3
/s) terhadap Le (Panjang Ekivalen)
Kurva hubungan Q (m3/s) terhadap Le (Panjang Ekivalen)
pada pipa D 1.25 in
y = 0.0007x
R2
= 1
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Le
Q(m3/s)
Kurva hubungan Q (m3/s) terhadap Le (Panjang Ekivalen)
pada pipa D 1 in
y = 0.0004x - 2E-18
R2
= 1
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Le
Q(m3/s)
Kurva hubungan Q (m3/s) terhadap F (friction Losses)
pada pipa D 0.75 in
y = 0.0003x + 7E-05
R2
= 0.9842
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
F
Q(m3/s)

18. Kurva hubungan Q (m3/s) terhadap Le (Panjang Ekivalen)
pada Elbow
y = 0.0007x + 6E-19
R2
= 1
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5
Le
Q(m3/s)
Kurva hubungan Q (m3/s) terhadap Le (Panjang Ekivalen)
pada sambungan T
y = 0.0007x + 6E-19
R2
= 1
0
0.00005
0.0001
0.00015
0.0002
0.00025
0.0003
0.00035
0.0004
0 0.1 0.2 0.3 0.4 0.5
Le
Q(m3/s)

19. BAB V
PEMBAHASAN
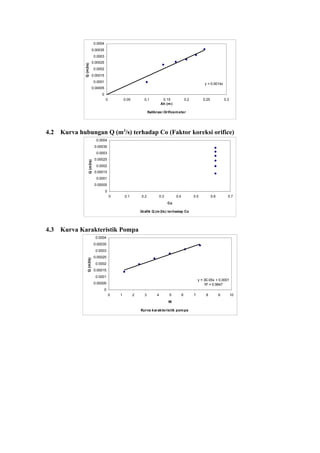
5.1. Pengaruh koofisien koreksi (Co) terhadap debit (Q)
Grafik Co terhadap Q (debit) berupa grafik dengan garis lurus sehingga dapat
disimpulkan dengan meningkatnya atau menurunya harga Q maka harga Co tidak akan
mengalami perubahan (konstan). Hal ini sesuai dengan perumusan hubungan Q
terhadap √∆h :
Q = Co.A2.
h
A
A
g
ƥ
−
−
])(1[
)(2
2
1
2
21
ρ
ρρ
Hal itu dapat terjadi karena koefisien orifice (Co) merupakan suatu faktor
koreksi dari adanya pengecilan atau pembesaran mendadak dalam sistem perpipaan,
sehingga dengan ukuran (diameter) Co yang tetap akan membuat faktor koreksi Co
bernilai konstan untuk setiap debit laju alir yang berbeda.
Dari data literatur, harga Co relatif konstan selama nilai NRe > 2000. Harga Co
untuk aliran turbulen sebesar 0.61 ( McCabe, Smith and Harriot ). Pada percobaan
didapat harga Co sebesar 0.61432, hasil ini cukup mendekati dengan harga Co dari
literatur.
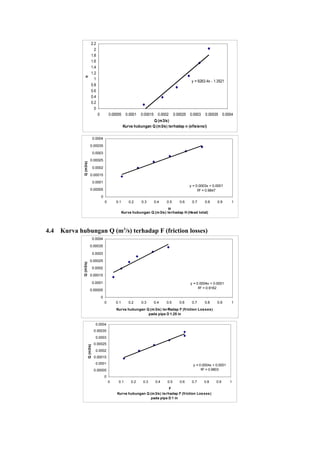
5.2. Pengaruh Friction losses (Ғ) pada pipa lurus terhadap debit (Q)
5.2.1 Diameter pipa berubah dengan debit tetap
Dari grafik Ғ terhadap Q dapat dilihat bahwa pipa yang diameternya paling kecil
memiliki nilai friction losses (Ғ) yang paling besar. Hal ini disebabkan oleh ruang
gerak fluida (air kran) untuk mengalir lebih sempit sehingga hampir seluruh
permukaan fluida (air kran) bergesekan dengan dinding pipa.
5.2.2 Diameter pipa tetap dan debit berubah
Dari grafik Ғ terhadap Q dapat dilihat nilai Ғ meningkat seiring dengan
meningkatnya laju alir volumetrik (Q). Hal ini dapat terjadi karena energi kinetik
yang dibawa oleh fluida sebagian berubah bentuk menjadi energi panas yang
dihasilkan oleh gesekan antara fluida dengan dinding pipa, sehingga dapat
disimpulkan semakin cepat fluida mengalir maka hilang energi akibat gesekan
akan semakin besar pula.

20. 5.3. Pengaruh Panjang Ekivalen (Le) terhadap Debit (Q)
Panjang ekivalen merupakan panjang pipa lurus yang mewakili panjang dari
sistem perlengkapan pipa dimana dapat memberikan friction losses yang sama dan
pressure drop yang sama. Dari grafik dapat dilihat semakin besar debit (Q) yang
diberikan maka panjang ekivalen yang diperlukan semakin besar pula.
5.4. Pengaruh Tinggi Tekan, Efisiensi, dan Kerja Pompa terhadap Debit (Q)
5.4.1 Pengaruh Efisiensi (η) pompa terhadap debit (Q)
Pada percobaan ini efisiensi pompa yang diperoleh kecil sekali. Hal ini disebabkan
oleh pengambilan sistem kontrol yang digunakan untuk menentukan efisiensi
pompa. Seharusnya sistem kontrol yang digunakan adalah sistem pompa. Tetapi
karena keterbatasan alat yang digunakan sistem yang dipakai adalah sistem yang
paling dekat dengan letak pompa yaitu sistem orificemeter.
5.4.2 Pengaruh kerja, daya, dan tinggi tekan total
Laju alir massa fluida yang di keluarkan semakin banyak jika laju alir yang
diberikan semakin besar. Untuk memperbesar laju alir tersebut, dibutuhkan daya
hisap pompa (P) yang besar sehingga kerja yang dihasilkan pompa (W) akan
semakin besar pula. Hal ini dapat dilihat dari grafik W terhadap Q dan P terhadap
Q dimana nilai P dan W meningkat seiring dengan bertambahnya nilai Q.
5.4.3 Pengaruh tinggi tekan total (H) terhadap debit (Q)
Tinggi tekan total yang dihasilkan dari percobaan ini adalah 0.4427m atau sekitar
45 cm. Nilai ini tidak sesuai dengan sistem yang digunakan pada percobaan yang
tingginya sekitar 180 cm. Hal ini disebabkan oleh sistem kontrol yang digunakan
bukan sistem pompa melainkan sistem yang terdekat dengan letak pompa yaitu
sistem kontrol orificemeter.

21. BAB VI
KESIMPULAN
 Harga Co yang diperoleh dari percobaan adalah 0.61432
 Friction losses untuk setiap pipa:
Untuk D = 1.25 in diperoleh harga Ғ = 0.2479 m2
/s2
Untuk D = 1.00 in diperoleh harga Ғ = 0.4132 m2
/s2
Untuk D = 0.75 in diperoleh harga Ғ = 0.5547 m2
/s2
 Panjang ekivalen untuk system perlengkapan pipa:
Valve 1 : 0.3667 m
Valve 2 : 0.6341 m
Valve 3 : 1.0286 m
Elbow : 0.3667 m
Sambungan T : 0.3667 m
 Karakteristik pompa ditentukan oleh kerja yang dihasilkan pompa, daya pompa,
efisiensi, dan tinggi tekan total dari pompa.dari percobaan ini diperoleh:
W : 4.3384 watt
P : 1.2364 watt
η : 0.9891 %
H : 0.4427 m

22. BAB VII
DAFTAR PUSTAKA
1. Mc.Cabe, Smith and Carnot, “Operasi Teknik Kimia I”, Terj. Ir.G. Jasjfi,
Erlangga,1999
2. Noel de Nevers, “Fluid Mechanics For Chemichal Engineering”, McGraw
Hill,1973.
3. Perry, J.H, “Chemichal Engineers Handbook”,McGraw Hill,1973.

23. Lampiran D
Contoh Perhitungan
D.1 Menentukan densitas air kran
3
3
/456.996
0261.0
0065.26
0261.0
793.996
0153.26
mkg
piknoV
airm
air
m
aquades
aquadesm
piknoV
=
=
=
=
=
=
ρ
ρ
D.2 Menentukan Viskositas air
cp
aqaqt
aqairairt
air
846.0
148.67*996.793
0.97156456.9965.129
=
∗∗
=
∗
∗∗
=
ρ
µρ
µ
D.3 Menghitung Gaya Gesekan pada pipa
Diameter 1.25 in
22
/062.0
456.996
1.0*8,9*)13600456.996(
.)(
sm
F
F
hgHgair
F
P
=
−
=
−=
∆−
−=
∆
ρ
ρρ
ρ
D.4 Menghitung Panjang Ekivalen
Pada Valve 1
m
Vf
DhgHgair
Le
2031.0
1451.0*1474.0*4*456.996
1.0*8,9*)13600456.996(
..4.
2..)(
2
2
=
−
−=
∆−
−=
ρ
ρρ
D.5 Menghitung faktor gesekan
Diameter 1.25 in

24. 0369.0
4.1*1451.0*2
035052.0*062.0
.2
.
2
2
=
=
=
LV
DF
f
D.6 Menghitung Koefisien Orifice
61432.0
1
46497.9
443.1
456.996
1.0.*8.9*)13600456.996(*2
*443.1
00014.0
1
.)(2
2
2
1
2
2
=








−





−
−
−
−
=








−





∆−
=
E
E
E
A
A
air
hgHgair
A
Q
Co
ρ
ρρ