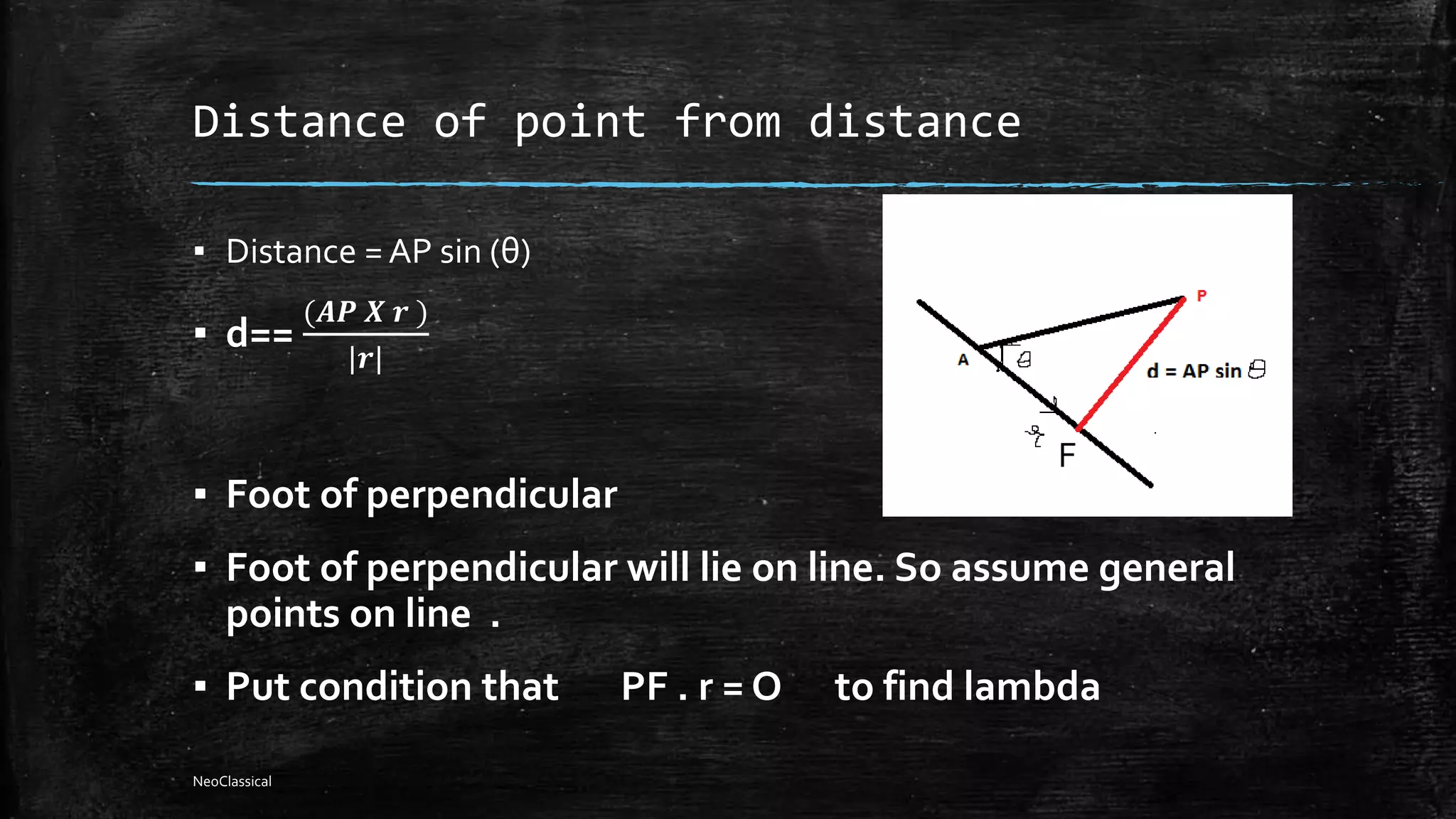
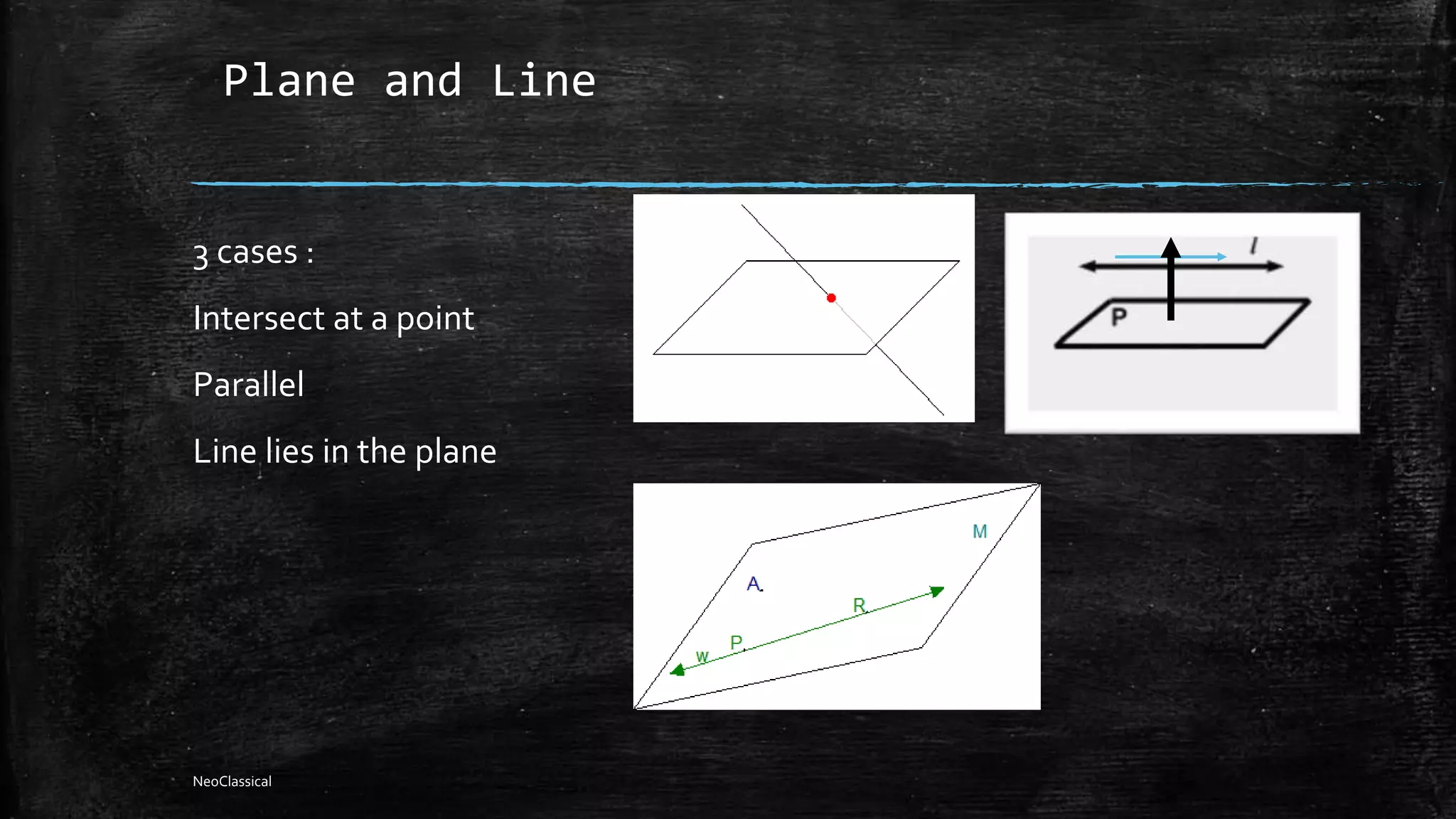
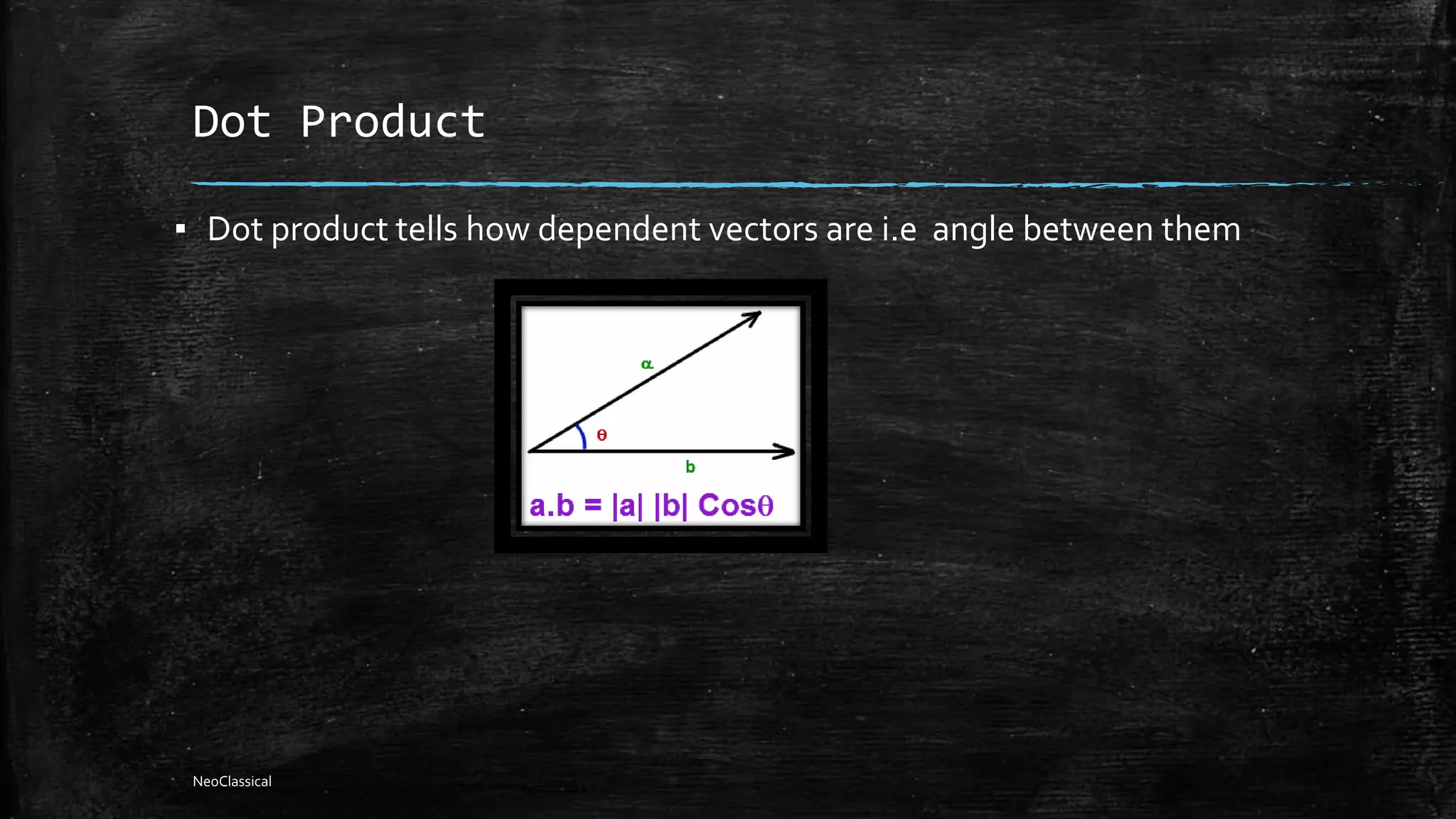
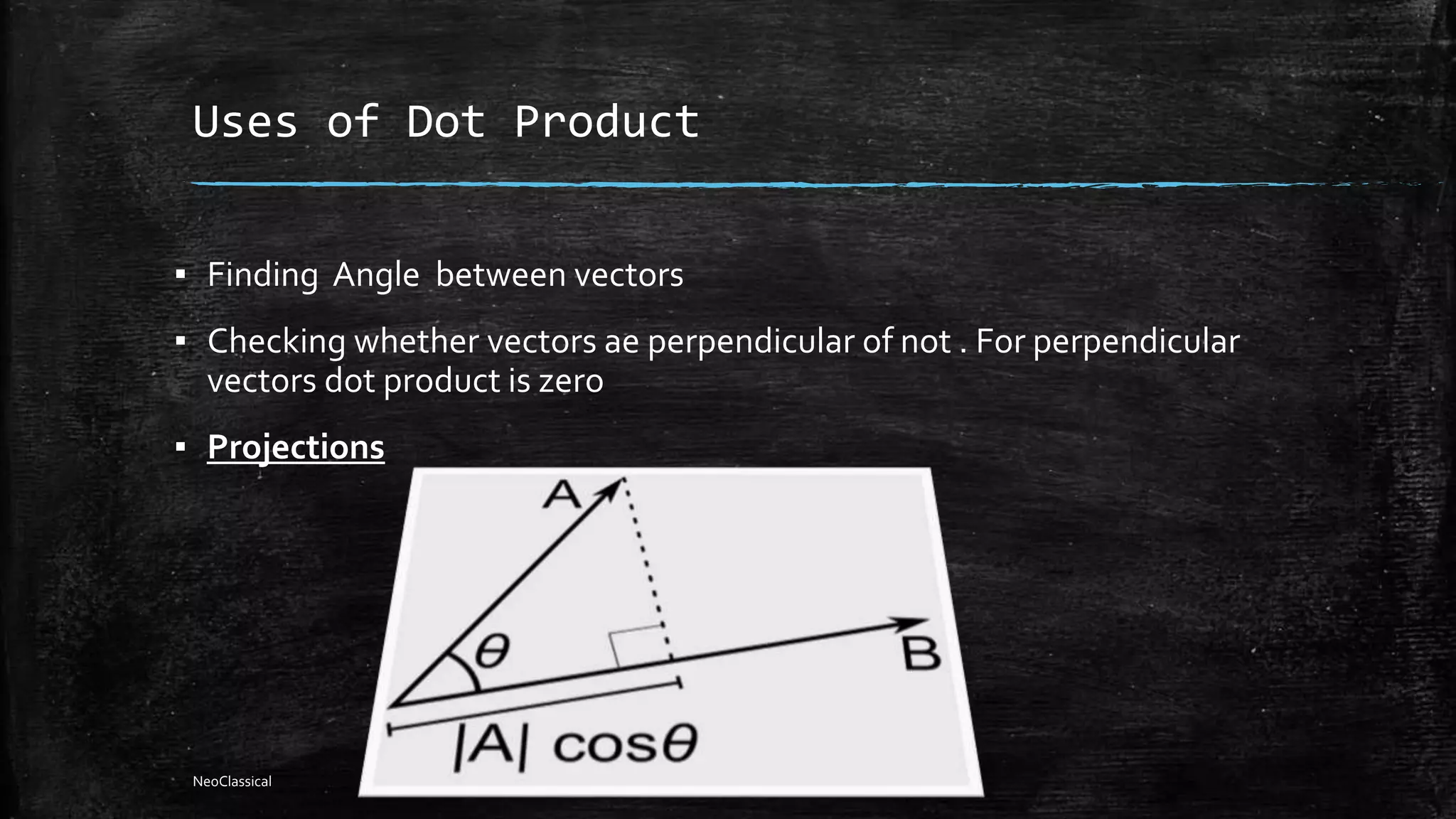
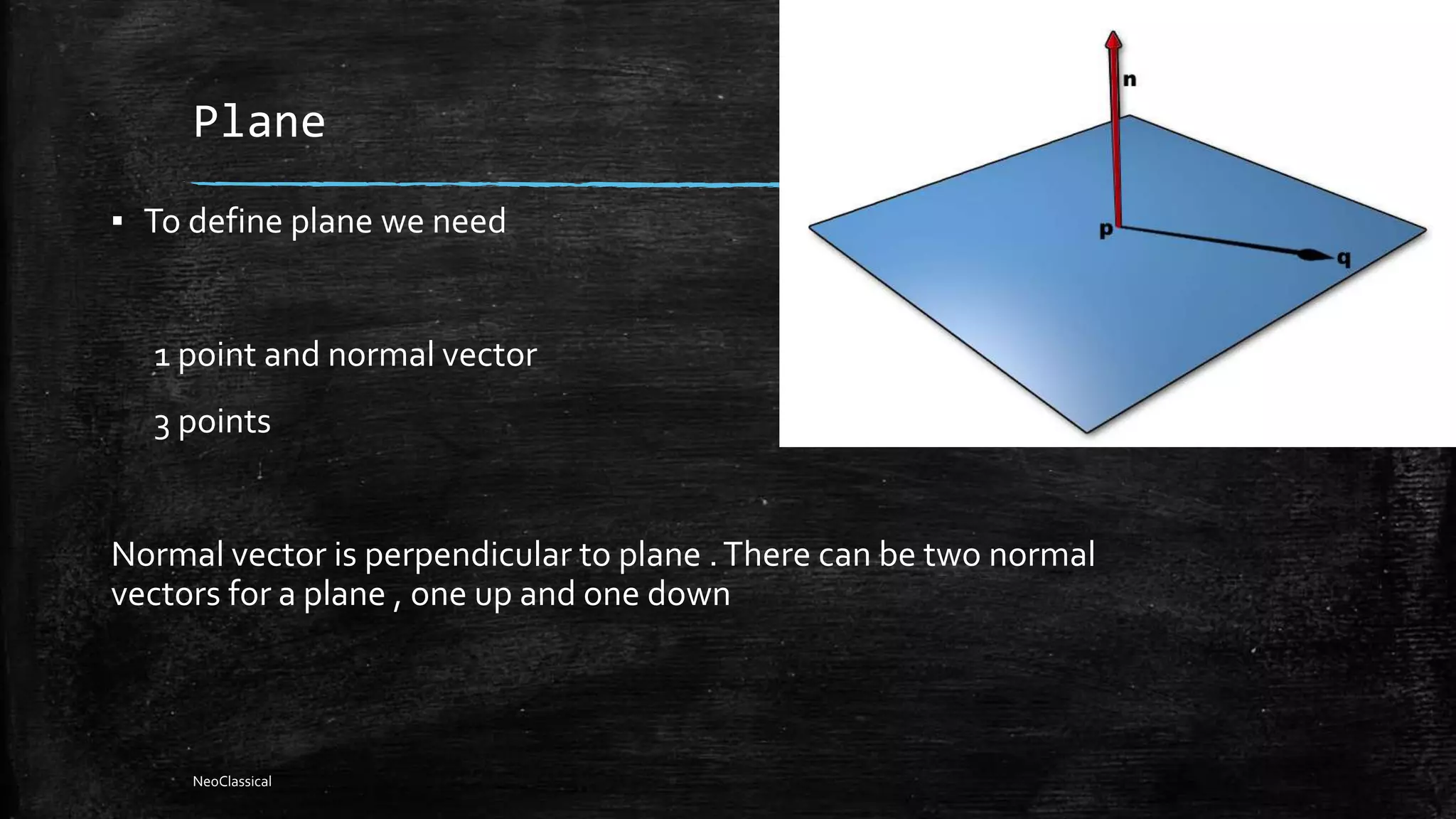
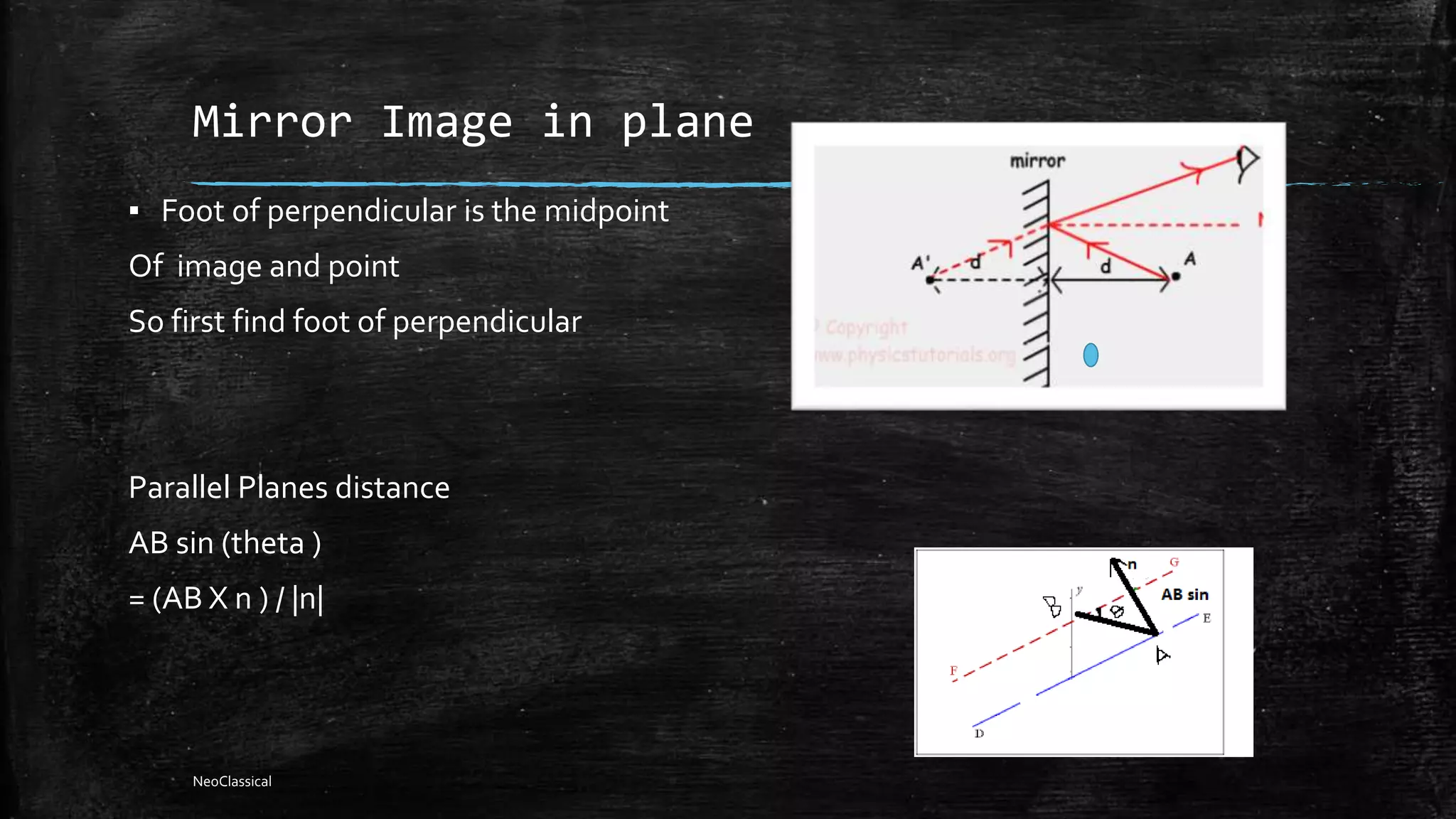
This document discusses various concepts related to vectors and 3D geometry including dot products, cross products, planes, lines, and their relationships. Dot products can be used to find the angle between vectors and determine if vectors are perpendicular. Cross products give a vector perpendicular to both input vectors. Plane equations can be defined using a point and normal vector, three points, or two vectors in the plane. Lines are defined by two points or a point and direction vector. The intersection of planes and lines, parallelism, and distances between lines and points and planes are also covered.

1. Vectors and 3D

2. Vector
▪ Head –Tail
Head
Tail
NeoClassical

3. Dot Product
▪ Dot product tells how dependent vectors are i.e angle between them
NeoClassical

4. Uses of Dot Product
▪ Finding Angle between vectors
▪ Checking whether vectors ae perpendicular of not . For perpendicular
vectors dot product is zero
▪ Projections
NeoClassical

5. ▪ Dot product can be used to find magnitude of a vector due to the following
property
a . a = |a|2
Example to find |A+B| we calculate
|A+B|2 = (A+B) .(A+B) = |A|2 + |B|2 + 2 A .B
Similarly for |A+B+C| we have to its dot product with itself
|A+B+C|2 = (A+B+C) .(A+B+C)
NeoClassical

6. CROSS PRODUCT
▪ AxB : Result is a vector ,whose magnitude is |A| |B| sin θ and direction is given
by right hand thumb rule
“(AxB) vector is perpendicular to both A and B  It is
perpendicular to plane containing A and B”
Whenever it is given to find out a vector perpendicular
to two vectors , cross product will be used
Example : Find a plane perpendicular to two given planes
, then the normal vector of third plane will be the
cross product of normal vectors of given planes
NeoClassical

7. ▪ Order is Important (AXB) ≠ (BXA)
▪ (AXB) = -(BXA)
▪ If vectors are give in rectangular coordinate system i.e in
terms of i,j,k
NeoClassical

8. Cross Product for calculating area
▪ Area of parallelogram :
Area of Triangle = ½ (A X B )
For calculation area of any other figure like quadrilateral , Pentagon just
break them into trianglesNeoClassical

9. ▪ For parallel vectors , Cross product is zero
If two vectors A and B are parallel : A = λ B
Example :
NeoClassical

10. Scalar Triple Product
▪ STP or box product = A.(BXC) denoted as [ A B C ]
▪ First cross product then dot product
▪ Geometric interpretation :Volume of Parallelepiped = [A B C ]
▪ Tetrahedron = (1/6) [A B C]
▪ A ,B ,C are adjacent sides
NeoClassical

11. Properties :
▪ Position of Dot and cross can be interchanged
A.(BXC) = (AXB).C
Can be cyclically permuted  [a b c] =[b c a] = [c a b]
If order is not maintained it becomes negative [ a b c] = - [ a c b]
Important : If Box product of three vectors A,B,C is zero ,
then they are coplanar . Reverse is also true
Coplanartiy :::Think of Box product
NeoClassical

12. Example
▪ Prove [ (a+b) (b+c) (c+a) ] = 2 [a b c ]
NeoClassical

13. Plane
▪ To define plane we need
1 point and normal vector
3 points
Normal vector is perpendicular to plane .There can be two normal
vectors for a plane , one up and one down
NeoClassical

14. Equation of plane
▪ Point on plane and normal vector is known
( r – a) . n = 0 r.n = a.n
In rectangular coordinate system Given point (x1,y1,z1)
a(x-x1) + b(y-y1) + c(z-z1) = 0
Coefficient of x , y and z give normal vector
Example : Plane = 3x+ 4y + 7z = 8
Normal vector  3 i + 4 j + 7 kNeoClassical

15. If two vectors in a plane are known
▪ As we know that normal vector is a vector perpendicular to plane .
So , if two vectors in plane are known , normal vector will be a vector
perpendicular to both these vectors
In the given figure , two vectors(Band C) in the plane (or parallel
to the plane) are known , So normal vector will be the cross
Product of Band C
n = (BXC)
NeoClassical

16. If three points are known
▪ Three points  Plane is fixed
Write any two vectors (AB , AC or BC )
These are in plane
Normal vector will be perpendicular to all of
these
n = (AB X BC) or (ACXBC) or (AB XAC)
Normal vector is known and point on plane is also known .
So we can equation of plane easily
NeoClassical

17. Perpendicular Distance of a point from
plane
▪ General Equation of plane  ax +by + cz =d
▪ Whenever we have to assume a plane , we will use general
equation of plane
NeoClassical

18. Foot of perpendicular
Equation of plane ax+by+cz=d
NormalVector : a i + b j +c k
Point Q (X1 , Y1 , Z1 )
Foot of perpendicular : X ( h,k,l )
Now QX is parallel to normal vector  QX = λ n
(h-X1)i + ( k-Y1 ) j + (l-Z1 ) = λ(a i + b j +c k)
 h = X1 + λ a , k =Y1 + λ b , l = Z1 + λ c
Put h,k,l in equation of plane and find λ
NeoClassical

19. Mirror Image in plane
▪ Foot of perpendicular is the midpoint
Of image and point
So first find foot of perpendicular
Parallel Planes distance
AB sin (theta )
= (AB X n ) / |n|
NeoClassical

20. Line
▪ For defining line we need
▪ Two points
▪ One point and slope
Direction vector is parallel to line
b  direction vector
NeoClassical

21. Equation of line
▪ One point and direction vector
▪ Direction vector = a i + b j + c k
▪ (Xo ,Y0 , Z0 )  Point on line
NeoClassical

22. If two points are given
▪ If two points are given , direction vector can be found out easily
A and B are given points , So AB is direction vector
Unit direction vector give direction cosine
Direction vector : a i + b j + c k
Unit direction vector (a i + b j + c k )/ √(𝑎2 + 𝑏2 + 𝑐2) √(𝑎2 + 𝑏2 + 𝑐2)
A
B
NeoClassical

23. ▪ General point on line = (Xo +λa,Y0 + λb, Z0 + λc)
NeoClassical

24. Line and Line
NeoClassical

25. ▪ Parallel : If their Direction vectors are parallel
Condition for Parrallel lines :
𝒂𝟏
𝒂𝟐
=
𝒃𝟏
𝒃𝟐
=
𝒄𝟏
𝒄𝟐
▪ A is point on Line 1
▪ B is point on line 2
▪ Distance = |AB sin θ |
|AB sin θ | is the magnitude of cross
Product ofAB and unit direction vector
ABsin(
NeoClassical

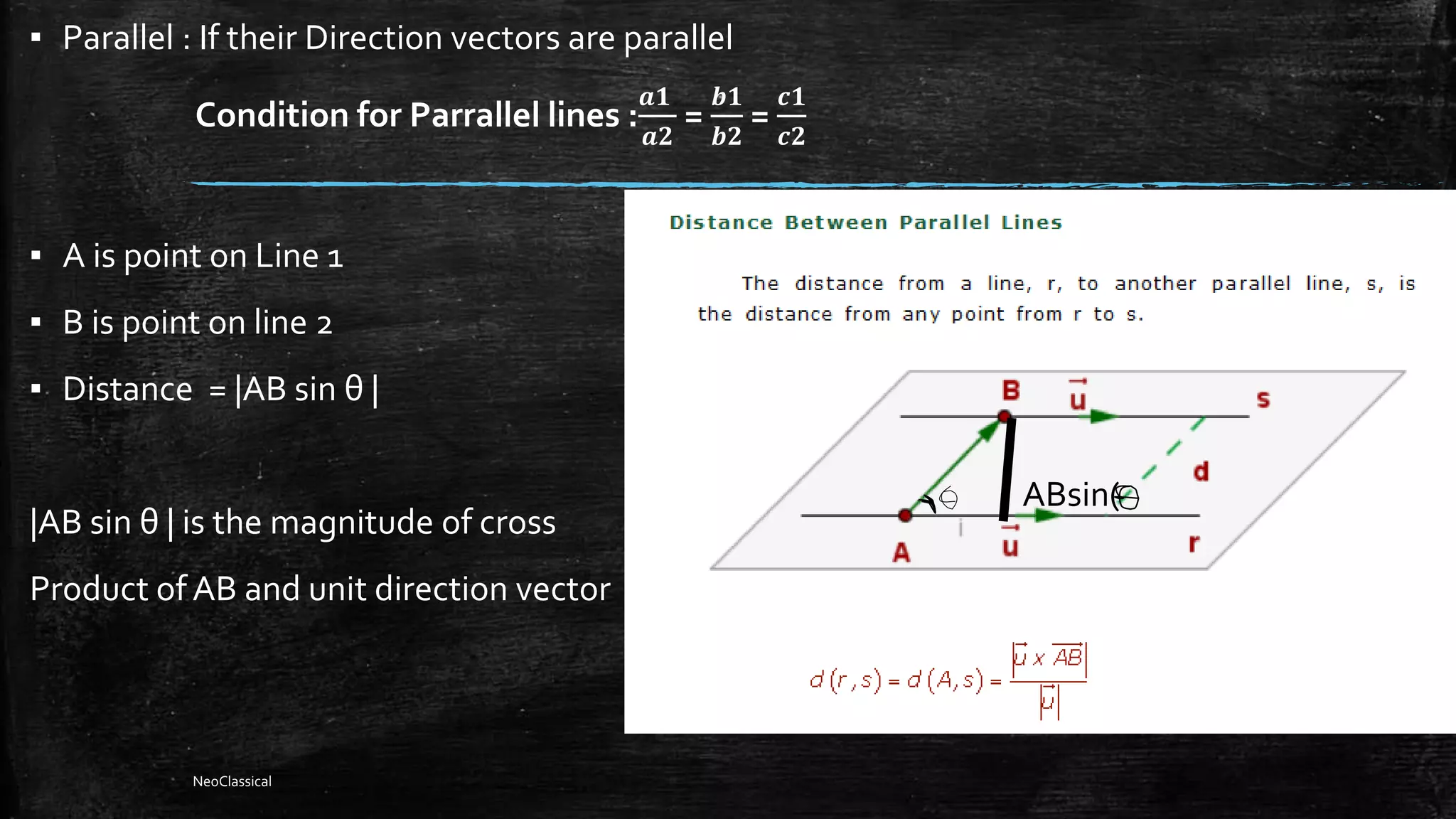
26. Distance between skew lines
▪ Skew lines are neither parallel nor intersecting
▪ Skew Lines have perpendicular direction vectors
▪ They form parallelepiped
▪ A is point on first line , B point on 2nd line
▪ Volume of parallelepiped = | [ u AB v ] |
▪ Volume = area X distance
▪ Area = |u X v|
NeoClassical

27. Point of Intersection
▪ First check whether they are parallel or not
▪ Assume general points on line and equate them
▪ Example :General points on Lines
Line 1: x= 4+t, y= 19+6t, z= 12+5t
Line 2: x= -3+2p, y= -15+8p, z= -19+8p
4+t= -3+2p 19+6t = -15+8p 12+5t = -19+8p
Solve any two to find t and p
But don’t forget to check the third equations .Lines may be skew
NeoClassical

28. ▪ 4 + 2t = 2 + s -5 + 4t = -1 + 3s 1 + 3t = 2s
▪ Solving 1 and 2 we get t=-5 and s =-8
▪ Putting this is third … LHS = -14 RHS = -16 (not satisfied)
▪ Lines are not parallel  they are skew
1) : x = 4 + 2t, y = -5 + 4t, z = 1 + 3t
2) : x = 2 + s, y = -1 + 3s, z = 2s
NeoClassical

29. Distance of point from distance
▪ Distance = AP sin (θ)
▪ d==
(𝑨𝑷 𝑿 𝒓 )
|𝒓|
▪ Foot of perpendicular
▪ Foot of perpendicular will lie on line. So assume general
points on line .
▪ Put condition that PF . r = O to find lambda
F
NeoClassical

30. Plane and Line
3 cases :
Intersect at a point
Parallel
Line lies in the plane
NeoClassical

31. ▪ If parallel Normal vector of plane and
Direction vector of plane will be perpendicular
▪ If line lies in plane then direction vector will be perpendicular to
normal vector plus point on line will lie on plane as well
▪ Example : Plane : 3x+y-z=4 Line : Direction : 1 i -2j + k Point (1,2,1)
Normal vector = 3i + j –k (1 i -2j + k). ( 3i + j –k ) = O
Also (1,2,1 ) satisfies 3x+y-z =4  Line lies in plane
n
NeoClassical

32. Point of intersection
▪ Assume General point on line
▪ Point of intersection will be the point common to both line and plane
, so it will satisfy the equation of plane also .
Put general point in plane’s equation and find parameter , λ
NeoClassical

33. Family of Planes
▪ Any plane passing through intersection of two planes P1 and P2 can be written as P1
+ λ P2 =O
▪ Whenever it is given that a plane passes through a intersection of planes take it as P1 +
λ P2 =O
▪ Angle b/w planes  Angle b/w their normal vectors
▪ Angle b/w lines  Angle b/wTheir direction vectors
▪ Angle b/w line and plane  90 – (Angle b/w Normal and direction vector)
NeoClassical

34. Distance of a point from plane measured
along line
Check this :
http://www.meritnation.com/ask-answer/question/find-the-distance-
of-the-point-1-2-3-from-the-plane-x-y-z/three-dimensional-
geometry/1811158
NeoClassical