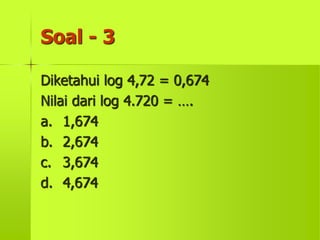
Logaritma adalah plog a = m, di mana p disebut bilangan pokok, a disebut bilangan logaritma, dan m disebut hasil logaritma. Logaritma dengan basis 10 biasanya ditulis tanpa basis 10. Sifat-sifat logaritma meliputi plog(ab) = plog a + plog b, plog(a/b) = plog a - plog b, dan plog(an) = n x plog a. Soal-soal logaritma meliputi menentukan nilai logaritma berdas

2. Pengertian Logaritma
Plog a = m artinya a = pm
Keterangan:
p disebut bilangan pokok
a disebut bilangan logaritma atau
numerus dengan a > 0
m disebut hasil logaritma atau eksponen
dari basis

3. Logaritma dengan basis 10
 Pada bentuk plog a = m, maka:
10log a = m cukup ditulis log a = m.
 Basis 10 pada logaritma tidak perlu
dituliskan.
 Contoh:
10log 3  dituliskan log 3
10log 5  dituliskan log 5

4. Sifat-sifat Logaritma
1. plog (a x b) = plog a + plog b
2. plog (a : b) = plog a - plog b
3. plog (a)n = n x plog a
n m
a = plog (a)n
m
4. plog
n
m plog a
=

6. Contoh Soal
1. Jika 2log x = 3
Tentukan nilai x = ….
Jawab:
2log x = 3  x = 23
x = 8.

7. Contoh Soal
2. Jika 4log 64 = x
Tentukan nilai x = ….
Jawab:
4log 64 = x  4x = 64
4x = 44
x = 4.

8. Contoh Soal
3. Nilai dari 2log 8 + 3log 9 = ….
Jawab:
= 2log 8 + 3log 9
= 2log 23 + 3log 32
= 3 + 2
= 5

9. Contoh Soal
4. Nilai dari 2log (8 x 16) = ….
Jawab:
= 2log 8 + 2log 16
= 2log 23 + 2log 24
= 3 + 4
= 7

10. Contoh Soal
5. Nilai dari 3log (81 : 27) = ….
Jawab:
= 3log 81 - 3log 27
= 3log 34 - 3log 33
= 4 - 3
= 1

11. Contoh Soal
6. Nilai dari 2log 84 = ….
Jawab:
= 2log 84
= 4 x 2log 23
= 4 x 3
= 12

12. Contoh Soal
7. Nilai dari 2log 84 = ….
Jawab:
= 2log 84 
= 2 x 2log 23
= 2 x 3
= 6
2
4 2log 8
=

13. Contoh Soal
8. Jika log 100 = x
Tentukan nilai x = ….
Jawab:
log 100 = x  10x = 100
10x = 102
x = 2.

15. Soal - 1
log 3 = 0,477 dan log 2 = 0,301
Nilai log 18 = ….
a. 1,552
b. 1,525
c. 1,255
d. 1,235

16. Pembahasan
log 3 = 0,477 dan log 2 = 0,301
log 18 = log 9 x 2
= log 9 + log 2
= log 32 + log 2
= 2 (0,477) + 0,301
= 0,954 + 0,301
= 1,255

17. Jawaban
log 3 = 0,477 dan log 2 = 0,301
Nilai log 18 = ….
a. 1,552
b. 1,525
c. 1,255
d. 1,235
c. 1,255

18. Soal - 2
log 2 = 0,301 dan log 5 = 0,699
Nilai log 5 + log 8 + log 25 = ….
a. 2
b. 3
c. 4
d. 5

19. Pembahasan
log 2 = 0,301 dan log 5 = 0,699
= log 5 + log 8 + log 25
= log 5 + log 23 + log 52
= log 5 + 3.log 2 + 2.log 5
= 0,699 + 3(0,301) + 2(0,699)
= 0,699 + 0,903 + 1,398
= 3,0

20. Jawaban
log 2 = 0,301 dan log 5 = 0,699
Nilai log 5 + log 8 + log 25 = ….
a. 2
b. 3
c. 4
d. 5
b. 3

21. Soal - 3
Diketahui log 4,72 = 0,674
Nilai dari log 4.720 = ….
a. 1,674
b. 2,674
c. 3,674
d. 4,674

22. Pembahasan
log 4,72 = 0,674
log 4.720 = log (4,72 x 1000)
= log 4,72 + log 1000
= log 4,72 + log 103
= 0,674 + 3
= 3,674

23. Jawaban
Diketahui log 4,72 = 0,674
Nilai dari log 4.720 = ….
a. 1,674
b. 2,674
c. 3,674
d. 4,674
c. 3,674

24. Soal - 4
Diketahui log 3 = 0,477 dan
log 5 = 0,699. Nilai log 135 = ….
a. 2,778
b. 2,732
c. 2,176
d. 2,130

25. Pembahasan
log 3 = 0,477 dan log 5 = 0,699.
log 135 = log (27 x 5)
= log 27 + log 5
= log 33 + log 5
= 3(0,477) + 0,699
= 1,431 + 0,699
= 2,130

26. Jawaban
Diketahui log 3 = 0,477 dan
log 5 = 0,699. Nilai log 135 = ….
a. 2,778
b. 2,732
c. 2,176
d. 2,130
d. 2,130

27. Soal - 5
Diketahui log 3 = a dan log 2 = b.
Maka log 18 = ….
a. 2a – b
b. 2a + b
c. a + 2b
d. a – 2b

28. Pembahasan
Diketahui log 3 = a dan log 2 = b.
log 18 = log (9 x 2)
= log 9 + log 2
= log 32 + log 2
= 2.log 3 + log b
= 2(a) + b
= 2a + b

29. Jawaban
Diketahui log 3 = a dan log 2 = b.
Maka log 18 = ….
a. 2a – b
b. 2a + b
c. a + 2b
d. a – 2b
b. 2a + b

30. Soal - 6
Diketahui plog 27 = 3x
Maka plog 243 = ….
a. 4x
b. 5x
c. 6x
d. 7x

31. Pembahasan
plog 27 = 3x
33 = p3x
Maka: x = 1 dan p = 3
plog 243 = 3log (3)5
= 5.3log 3
= 5 . X
= 5x

32. Jawaban
Diketahui plog 27 = 3x
Maka plog 243 = ….
a. 4x
b. 5x
c. 6x
d. 7x
b. 5x

33. Soal - 7
Diketahui log 2 = 0,301
Maka log 50 = ….
a. 0,699
b. 1,301
c. 1,699
d. 2,301

34. Pembahasan
log 2 = 0,301
log 50 = log (100 : 2)
= log 100 – log 2
= log 102 – log 2
= 2 – 0,301
= 1,699

35. Jawaban
Diketahui log 2 = 0,301
Maka log 50 = ….
a. 0,699
b. 1,301
c. 1,699
d. 2,301
c. 1,699

36. Jangan Lewatkan
Program Khusus
Pembahasan Soal-soal
UN 2001 s.d. 2005