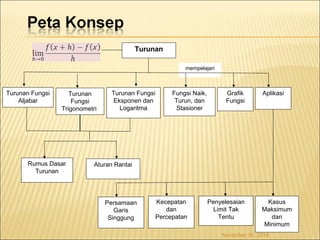
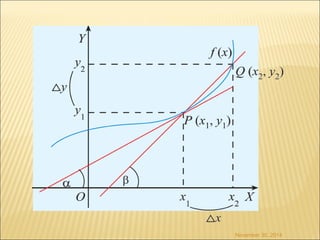
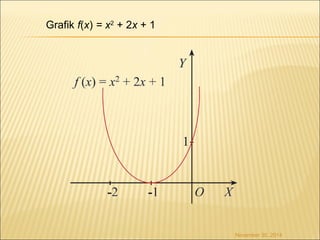
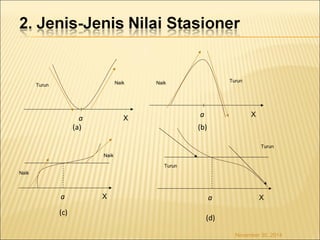
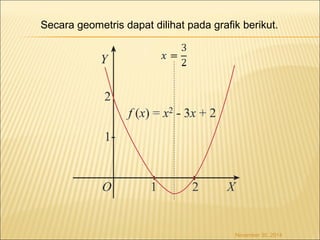
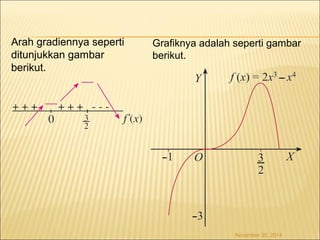
Dokumen ini membahas konsep turunan dalam kalkulus, mencakup definisi, aturan dasar, aplikasi dalam menentukan maksimum dan minimum, serta berbagai contoh fungsi. Terdapat penjelasan tentang cara menghitung turunan fungsi aljabar, eksponen, logaritma, dan trigonometri, serta cara menganalisis grafik fungsi. Beberapa metode dalam menentukan kecepatan, percepatan, dan limit tak tentu juga diuraikan dalam konteks penggunaan turunan.

1. Bab 8
Turunan
November 30, 2014

2. Turunan
mempelajari
Kasus
Maksimum
dan
Minimum
Penyelesaian
Limit Tak
Tentu
Kecepatan
dan
Percepatan
Rumus Dasar Aturan Rantai
Turunan
Persamaan
Garis
Singgung
Grafik Aplikasi
Fungsi
Fungsi Naik,
Turun, dan
Stasioner
Turunan Fungsi
Eksponen dan
Logaritma
Turunan Fungsi
Aljabar
November 30, 2014
Turunan
Fungsi
Trigonometri

3. 1. Tentukan gradien dari garis f(x) = x2 + 2x di titik (a, b).
2. Diketahui f’(x) = 2x + 2. Tentukan .
3. Samakan hasil 1 dan 2? Apa sebenarnya hubungan antara
soal 1 dan 2?
November 30, 2014

4. 1. Pengertian Turunan
Turunan suatu fungsi f(x) didefinisikan sebagai berikut.
Bentuk limit sudah disinggung di Bab 7.
Coba diingat lagi!
November 30, 2014

5. Contoh:
Dengan menggunakan definisi turunan, tentukan turunan
pertama fungsi f(x) = x2 + 1.
Jawab:
November 30, 2014

6. 2. Turunan Ditinjau Dari Sudut Pandang Geometri
Misalkan diketahui fungsi y = f(x). Secara geometri turunan
fungsi diartikan sebagai gradien (kemiringan).
Gradien garis singgung di titik P(a, b) yang terletak pada
fungsi y = f(x) adalah sebagai berikut.
m = f’(a) =
f a h f a
) ( ) ( lim0
Secara geometris, ilustrasinya dapat dilihat pada gambar
berikut.
November 30, 2014
h
h
+ -
®

7. November 30, 2014

8. Contoh:
Tentukan gradien garis singgung kurva yang memiliki
persamaan untuk x ≠ 0 di x = 2.
Jawab:
Gradien garis singgung kurva y = f(x) untuk x = 2 adalah
m = f'(2) = –1.
Dengan kata lain, laju perubahan fungsi f(x) di x = 2 adalah –1.
November 30, 2014

9. Jika n bilangan rasional, a dan c konstanta sedangkan f'(x)
turunan dari f(x) maka berlaku rumus turunan
Jika f(x) = c maka turunannya adalah f'(x) = 0.
Jika f(x) = xn maka turunannya adalah f'(x) = nxn – 1.
Jika f(x) = axn maka turunannya adalah f'(x) = anxn – 1.
November 30, 2014

10. Contoh:
Tentukan turunan dari f(x) = 6x4.
Jawab:
f(x) = 6x4
Mengacu rumus di atas, diperoleh nilai
a = 6
n = 4
Jadi, f'(x) = 6(4x4 – 1)
= 24x3
November 30, 2014

11. 1. Turunan Fungsi Sinus
Jika f(x) = sin x, maka turunannya adalah f'(x) = cos x
2. Turunan Fungsi Kosinus
Jika f(x) = cos x, maka turunannya adalah f'(x) = –sin x.
Dengan menggunakan rumus
akan diperoleh
a. Jika f(x) = a sin x maka f'(x) = a cos x.
b. Jika f(x) = a cos x maka f'(x) = –a sin x.
c. Jika f(x) = tan x maka f'(x) = sec2 x.
d. Jika f(x) = csc x maka f'(x) = –csc x cot x.
e. Jika f(x) = sec x maka f'(x) = sec x tan x.
f. Jika f(x) = cot x maka f'(x) = –csc2 x.
November 30, 2014

12. a. f(x) = c u(x), turunannya f'(x) = c u'(x).
b. f(x) = u(x) ± v(x), turunannya f'(x) = u'(x) ± v'(x).
c. f(x) = u(x) v(x), turunannya f'(x) = u'(x) v(x) + u(x) v'(x).
u x
d. f(x) = , v(x) ≠ 0, turunannya
e. f(x) = u(x)n, turunannya f'(x) = n(u(x))n – 1u'(x).
f x = u x v x -u x v x ( )
'( ) '( ) ( ) ( ) '( ) v 2 ( x
)
November 30, 2014
( )
v x

13. Contoh:
Tentukan f'(x) jika diketahui f(x) = (7x2 – 5)8.
Jawab:
f(x) = {u(x)}8
u(x) = 7x2 – 5
Dengan demikian, u'(x) = 14x.
f'(x) = 8(7x2 – 5)8 – 1 (14x)
= 112(7x2 – 5)7
Jadi, f'(x) = 112(7x2 – 5)7.
November 30, 2014

14. Misal terdapat fungsi y = f(u(x)), turunan fungsinya
ditentukan dengan rumus
Misalkan terdapat fungsi y = f(u(v(x))), turunan fungsinya
dapat ditentukan dengan
November 30, 2014

15. Contoh 1:
Tentukan turunan fungsi y = (3x – 2)2.
Jawab:
Misalkan u = 3x – 2. Dengan demikian,
y = u2 Þ
u = 3x – 2 =
Jadi,
= 2u × 3 = 2(3x – 2)(3) =18x – 12.
November 30, 2014

16. Contoh 2:
Tentukan turunan fungsi y = cos (sin (2x – 1 )).
Jawab:
Misalkan u = 2x – 1
v = sin u
y = cos v
November 30, 2014

17. 1. Turunan Fungsi Eksponen (y = ex)
Jika y = ex maka y' = ex.
Secara umum, dapat ditentukan turunan fungsi y = eax + b
Jika y = eax + b maka y' = aeax + b
November 30, 2014

18. Contoh:
Tentukan turunan dari fungsi berikut.
a. y = e5x
b. y = e–x + 3
Jawab:
a. y = e5x maka y' = 5e5x
b. y = e –x + 3 maka y' = –e –x + 3
November 30, 2014

19. ln x = y Û x = ey Jika y = ln x maka
Secara umum, dapat ditentukan turunan y = ln u, dengan
u = f(x), adalah sebagai berikut.
Jika y = ln u, dengan u = f(x) maka
November 30, 2014

20. Perhatikan turunan fungsi-fungsi berikut.
a. y = 2 ln x maka
b. y = ln (kx + c)
Misalkan u = kx + c. Oleh karena itu, u' = k
sehingga
c. y = ln (6x5 – 3x2 + 2x)
u = 6x5 – 3x2 + 2x.
Oleh karena itu, u' = 30x4 – 6x + 2
sehingga
November 30, 2014

21. 1. Pengertian Fungsi Naik, Fungsi Turun, dan Nilai
Stasioner
f(x)
Grafik fungsi f(x) naik pada interval a < x < b dan interval
d < x < e.
Grafik fungsi turun pada interval b < x < c.
Grafik fungsi tidak naik dan tidak turun (stasioner) pada
interval c < x < d.
November 30, 2014
Y
0 a b C d e X

22. Cara menentukan interval suatu fungsi naik atau turun.
Misalkan diberikan fungsi y = f(x).
a. Grafik f(x) naik jika f'(x) > 0.
b. Grafik f(x) turun jika f'(x) < 0.
c. Grafik f(x) stasioner (tidak naik dan tidak turun) jika f'(x) = 0.
November 30, 2014

23. Contoh:
Tentukan interval yang menyebabkan fungsi f(x) = x2 + 2x + 1
naik atau turun, serta titik stasionernya.
Jawab:
f(x) = x2 + 2x + 1 Þ f'(x) = 2x + 2 = 2(x + 1).
Fungsi naik jika f'(x) > 0 Þ 2(x + 1) > 0 Û x > –1.
Fungsi turun jika f'(x) < 0 Þ 2(x + 1) < 0 Û x < –1.
Fungsi stasioner jika f'(x) = 0 Þ 2(x + 1) = 0 Û x = –1
sehingga f(–1) = 0. Jadi, titik stasionernya (–1, 0).
Secara geometris, dapat dilihat pada grafik f(x) = x2 + 2x + 1
berikut.
November 30, 2014

24. November 30, 2014
Grafik f(x) = x2 + 2x + 1

25. Turun Naik
a X
Naik Turun
a X
Naik
a X
Naik
(a) (b)
(c)
Turun
a X
Turun
(d)
November 30, 2014

26. Misalkan x = a adalah stasioner.
 Jika pada x < a, f(x) turun dan x > a , f(x) naik maka
x = a adalah titik balik minimum. (Gambar (a))
 Jika pada x < a ,f(x) naik dan x > a, f(x) turun maka x = a
adalah titik balik maksimum. (Gambar (b))
 Jika pada x < a, f(x) naik dan x > a, f(x) juga naik
maka x = a adalah titik belok. (Gambar (c))
 Jika pada x < a, f(x) turun dan x > a, f(x) juga turun
maka x = a adalah titik belok. (Gambar (d))
November 30, 2014

27. Contoh:
Tentukan nilai-nilai stasioner fungsi f(x) = x2 – 3x + 2 dan
jenisnya.
Jawab:
f(x) = x2 – 3x + 2 Þ f'(x) = 2x – 3.
Nilai stasioner dicapai jika f'(x) = 0, yaitu di titik .
Untuk fungsinya turun.
Untuk maka fungsinya naik.
Dengan demikian, nilai stasioner pada yaitu
adalah titik balik minimum, tepatnya adalah titik November 30, 2014

28. Secara geometris dapat dilihat pada grafik berikut.
November 30, 2014

29. Dalam menggambar grafik suatu fungsi f(x), langkah-langkah
yang perlu kalian perhatikan adalah sebagai
berikut.
1. Menentukan titik potong fungsi f(x) dengan sumbu-sumbu
koordinat (sumbu X dan sumbu Y).
2. Menentukan titik-titik stasioner atau titik ekstrem dan
jenisnya.
3. Menentukan titik-titik sembarang dalam fungsi untuk
memperhalus grafik.
November 30, 2014

30. Contoh:
Sketsalah grafik fungsi f(x) = 2x3 – x4.
Jawab:
Langkah 1:
f(x) = 2x3 – x4 = x3(2 – x) = 0
x = 0 atau x = 2 Þ (0, 0) dan (2, 0).
Titik potong dengan sumbu Y, x = 0 sehingga f(0) = 0 Þ (0, 0)
Langkah 2:
f(x) = 2x3 – x4 Þ f'(x) = 6x2 – 4x3 = 2x2(3 – 2x) = 0
x = 0 atau
November 30, 2014

31. a) Untuk x = 0
Untuk x < 0 maka f'(x) > 0 Þ fungsi f(x) naik.
Untuk x = 0 merupakan nilai di mana terdapat titik belok
Untuk maka f'(x) > 0 Þ f(x) naik.
Jadi x = 0 merupakan nilai di mana terdapat titik belok.
b) Untuk
Untuk maka f'(x) > 0 Þ f(x) naik.
Untuk maka f'(x) < 0 Þ f(x) turun.
Jadi titik balik maksimum
November 30, 2014

32. Grafiknya adalah seperti gambar
berikut.
November 30, 2014
Arah gradiennya seperti
ditunjukkan gambar
berikut.

33. 1. Menentukan Persamaan Garis Singgung Kurva
 Persamaan garis di titik (a, b) dan bergradien m adalah
y – b = m(x – a).
 Karena gradien garis singgung f(x) di titik (a, b) adalah
y' = f'(a), persamaannya dapat dirumuskan dengan
y – b = f'(a)(x – a)
November 30, 2014

34. Contoh:
Tentukan persamaan garis singgung fungsi f(x) = x2 di titik
(2, 4).
Jawab:
f(x) = x2
f'(x) = 2x.
f'(2) = 2(2) = 4.
Oleh karena itu, persamaan garis singgungnya adalah
y – 4 = 4(x – 2)
Û y = 4x – 4
November 30, 2014

35. 2. Perhitungan Kecepatan dan Percepatan
s
D
Kecepatan rata-rata = v(t) =
Ds = perubahan jarak; Dt = perubahan waktu.
Jika Δt → 0, kecepatan v(t) dirumuskan dengan
ds
v(t) = atau v(t) =
s
D
lim
Misalkan percepatan pada saat t dinotasikan dengan a(t).
a(t) =
November 30, 2014
t
D
dt
t
t D
D ®0
2
2
dt
d s
dv ÷ø
çè
= d
æ
ds
ö = dt
dt
dt

36. Contoh:
Suatu benda bergerak sepanjang garis lurus. Jarak yang
ditempuh benda tersebut dalam waktu t detik adalah
meter.
Tentukan kecepatan benda pada waktu t = 2 detik.
Jawab:
Kecepatan benda saat t = 2 detik adalah sebagai berikut.
v(t) = = 2t2 – 9t + 10
v(2) = 2(2)2 – 9(2) + 10
Hal ini berarti pada saat t = 2 detik, benda berhenti sesaat
karena pada waktu itu kecepatannya nol.
November 30, 2014
ds
dt

37. 3. Menentukan Limit Tak Tentu
Salah satu manfaat turunan adalah menentukan nilai limit
fungsi jika limit tersebut memiliki bentuk tak tentu. Aplikasi ini
sering disebut dengan dalil L’Hopital.
Jika f(x) dan g(x) memiliki turunan di x = a dan f(a) = g(a) = 0,
sedangkan f'(a) dan g'(a) tidak nol, berlaku rumus berikut.
November 30, 2014
f a
'( )
'( )
f x
lim '( )
= =
'( )
f x
lim ( )
( )
g a
g x
g x
x ® a x ®
a

38. Contoh:
Tentukan nilai .
Jawab:
f(x) = x – 2
g(x) = x2 – 4
Kita cek, f(2) = 0 dan g(2) = 0. Akibatnya, .
Kita gunakan dalil L’Hopital:
Diperoleh f'(x) = 1 dan g'(x) = 2x.
1
lim 1
-
lim 2
Jadi, .
November 30, 2014
4
® x ® 2
x
2 2 2
4
= =
-
x
x x

39. 4. Menyelesaikan Kasus Maksimum atau Minimum
Contoh:
Suatu persegi panjang mempunyai keliling 200 cm.
Tentukan panjang dan lebarnya agar luas bangun itu
maksimum.
Jawab:
Misalkan panjang = p dan lebarnya = l.
Kelilingnya adalah
K = 2p + 2l
Û 200 = 2p + 2l
Û p = 100 – l
Luasnya L = pl = (100 – l)l = 100l – l2.
November 30, 2014

40. Agar luasnya maksimum, turunan fungsi L harus nol.
November 30, 2014
=100 – 2l = 0 Û l = 50
ds
dt
p = 100 – l
= 100 – 50
= 50
Dengan demikian, agar luas bangun itu maksimum,
lebarnya 50 cm dan panjangnya 50 cm.