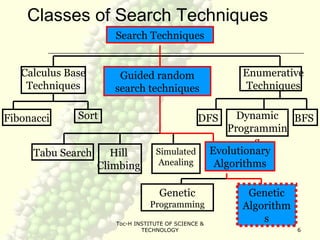
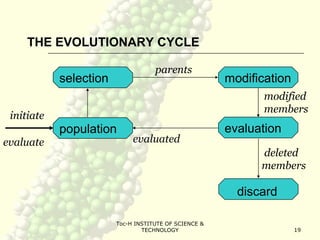
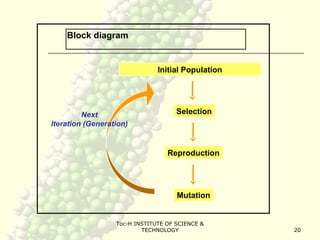
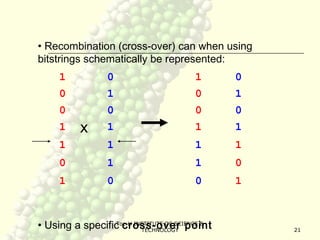
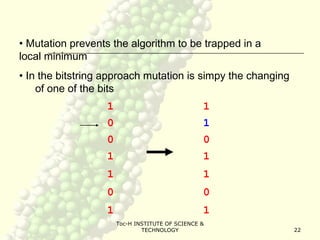
Genetic algorithms (GA) are a class of optimization algorithms inspired by biological evolution. GAs use concepts like natural selection and genetic inheritance to evolve solutions to problems by iteratively selecting better solutions. A GA encodes potential solutions as strings called chromosomes and uses genetic operators like crossover and mutation to generate new solutions, evaluating them to select the fittest ones. This process is repeated until a termination condition is reached, such as a solution meeting criteria or a fixed number of generations. GAs are well-suited for complex problems where little is known about the search space.

1. Toc-H INSTITUTE OF SCIENCE & TECHNOLOGY 1
Introduction to
Genetic Algorithms
BY
PREMSANKAR.C
CS S7
ROLL NO :25

2. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 2
Genetic Algorithms (GA) Overview
 Originally developed by John Holland (1975)
 A class of optimization algorithms
 Inspired by the biological evolution process
 Uses concepts of “Natural Selection” and
“Genetic Inheritance” (Darwin 1859)
 Particularly well suited for hard problems where
little is known about the underlying
search space
 Widely-used in business, science and
engineering
 GA’s are a subclass of Evolutionary Algorithm

3. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 3
History of GA’s
Evolutionary computing developed in
the 1960’s.
GA’s were created by John Holland in
the mid-70’s.
 The computer model introduces
simplifications (relative to the real
biological mechanisms)
General Introduction to GA’s

4. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 4
INTRODUCTION
 genetic algorithms are best for
searching for new solutions
 making use of solutions that have
worked well in the past
 It works on large population of
solutions that are repeatedly
subjected to selection pressure
(survival of the fittest)

5. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 5
 Each solution is encoded as a
chromosome (string) also called a
genotype
 chromosome is given a measure of
fitness via a fitness function.
Possible information encoding
 Bit strings (0101 ... 1100)
 Real numbers (43.2 -33.1 ... 89.2)
 Permutations of element (E11 E3 E7 ... E1 E15)
 Lists of rules (R1 R2 R3 ... R22 R23)
 Program elements (genetic programming)

6. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 6
Classes of Search Techniques
Search Techniques
Calculus Base
Techniques
Guided random
search techniques
Enumerative
Techniques
BFSDFS Dynamic
Programmin
g
Tabu Search Hill
Climbing
Simulated
Anealing
Evolutionary
Algorithms
Genetic
Programming
Genetic
Algorithm
s
Fibonacci Sort

7. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 7
Genetic Algorithms vs Traditional
Algorithm
1.GA’s work with a coding of parameter set,
not the parameter themselves.
2.GA’s search from a population of points,
not a single point.
3. Application of GA operators causes
information from the previous
generation to be carried over to the next.
4.GA’s use probabilistic rules, not
deterministic rules.

8. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 8
BASIC Components of a GA
A problem definition as input, and
 Encoding principles (gene, chromosome)
 Initialization procedure (creation)
 Selection of parents (reproduction)
 Genetic operators (mutation, recombination)
 Evaluation function (environment)
 Termination condition

9. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 9
Initialization
Start with a population of randomly generated
individuals, or use
- A previously saved population
- A set of solutions provided by a human expert
- A set of solutions provided by another heuristic
algorithm

10. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 10
ENCODING
 Each chromosome has one binary string.
Each bit in this string can represent some
characteristic of the solution.
 The binary string of chromosome example

11. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 11
FITTNESS FUNCTION
 Determine the fitness of each
member of the population
 Perform the objective function on
each population member
 . FitnessScaling adjusts down the
fitness values of the super-
performers and adjusts up the lower
performers.

12. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 12
Genetic Operators
 Three major operations of genetic algorithm
are
Selection replicates the most successful
solutions found in a population
Recombination decomposes two distinct
solutions and then randomly mixes their parts
to form new solutions
 Mutation randomly changes a candidate
solution(0-1)

13. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 13
MUTATIONMUTATION
Purpose: to simulate the effect of errors that
happen with low probability during duplication
For binary encoding we can switch randomly
chosen bits from 1 to 0 or from 0 to 1.
Results:
- Movement in the search space
- Restoration of lost information to the population

14. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 14
SELECTION(reproduction)
 Purpose: to focus the search in
promising regions of the space
 Inspiration: Darwin’s “survival of
the fittest” .
 Example: the probability of
selecting a string with a fitness
value of f is f/ft, ft is the sum of all
of the fitness values in the
population

15. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 15
CROSSOVERCROSSOVER (Recombination )
 A. One-point crossover
B. Two-point crossover
•Crossover selects genes from parent chromosomes
and creates a new one
•choose some crossover point
•everything before this point copies from the first
parent and then everything after the crossover copies
from the second parent
•Causes an exchange of genetic material between
two parents

16. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 16
Single Point Crossover Example
Parent 1 1 0 0 $ 1 0 0 1 0 1 0
Parent 2 0 0 1 $ 0 1 1 0 1 1 1
Child 1 1 0 0 $ 0 1 1 0 1 1 1
Child 2 0 0 1 $ 1 0 0 1 0 1 0
Double Point Crossover Example
Parent 1 1 1 0 1 0 0 $ 1 0 0 1 $ 0 1 1
Parent 2 0 1 0 1 1 0 $ 0 0 1 0 $ 1 0 1
Child 1 1 1 0 1 0 0 $ 0 0 1 0 $ 0 1 1
Child 2 0 1 0 1 1 0 $ 1 0 0 1 $ 1 0 1

17. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 17
Termination condition
 A solution is found that satisfies minimum
criteria
 Fixed number of generations reached
 Allocated budget (computation
time/money) reached
 The highest ranking solution's fitness is
reaching
 A satisfactory solution has been achieved
 No improvement in solution quality

18. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 18
SIMPLE GENETIC ALGORITHM
1. Create a Random Initial State
2. Evaluate Fitness
3. Crossover ( recombination)
4. Reproduce
5. Repeat until successful.
6. Terminate

19. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 19
THE EVOLUTIONARY CYCLE
selection
population evaluation
modification
discard
deleted
members
parents
modified
members
evaluated
initiate
evaluate

20. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 20
Initial Population
Selection
Reproduction
Mutation
Next
Iteration (Generation)
Block diagram

21. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 21
• Recombination (cross-over) can when using
bitstrings schematically be represented:
• Using a specific cross-over point
1
0
0
1
1
0
1
0
1
0
1
1
1
0
X
1
0
0
1
1
1
0
0
1
0
1
1
0
1

22. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 22
• Mutation prevents the algorithm to be trapped in a
local minimum
• In the bitstring approach mutation is simpy the changing
of one of the bits
1
0
0
1
1
0
1
1
1
0
1
1
0
1

23. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 23
ADVANTAGES OF GENETIC ALGORITHMS
 A fastest search technique
 GAs will produce "close" to optimal
results in a "reasonable" amount of
time
 Suitable for parallel processing
 Fairly simple to develop
 Makes no assumptions about the
problem space

24. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 24
DRAWBACKS
 Number of permutations of functions and
variables. The search space is vast.
 Most GPs are limited in the available
operators and terminals they can use.
 It requires a lot of computer work, even
when a good set of operations, terminals
and controlling algorithm are chosen

25. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 25
APPLICATIONS OF GENETIC ALGORITHMS
 genetic programming
 Scheduling: Facility, Production, Job, and
Transportation Scheduling
 Design: Circuit board layout, Communication
Network design, keyboard layout, Parametric
design in aircraft
 Machine Learning: Designing Neural
Networks, Classifier Systems, Learning rules
 Image Processing: Pattern recognition

26. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 26
CONCLUSION
 GAs are a powerful tool for global
search
 GA are best for searching for new
solutions and making use of
solutions that have worked well in
the past

27. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 27
ANY OUESTIONS ?

28. Toc-H INSTITUTE OF SCIENCE &
TECHNOLOGY 28