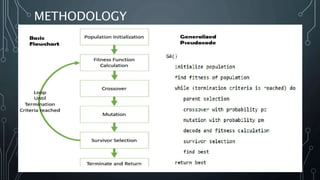
The document discusses genetic algorithms, which are optimization techniques inspired by Darwinian evolution and utilize processes like selection, crossover, and mutation to evolve solutions over generations. A numerical example illustrates the application of a genetic algorithm to solve the equation a +2b +3c +4d = 30, detailing steps including initialization, evaluation, selection, crossover, and mutation. The process continues iteratively to improve fitness until satisfactory results are achieved.

1. GENETIC-ALGORITHM
PRESENTATION
ARTIFICIAL INTELLIGENCE

2. GROUP-MEMBERS
• M. Usama Razzaq 2013-MC-159
• M. Talal Pansota 2013-MC-161
• M. Zubair 2013-MC-165
• Jahanzeb Kahout 2013-MC-167
• S. M. Jari Abbas 2013-MC-169
• Asif Nawaz 2013-MC-173
• Hamza Saeed 2013-MC-179
• M. Farooq 2013-MC-181

3. INTRODUCTION
• Genetic Algorithm is based on the heuristic method “survival of
the fittest”, Unlike the conventional exhaustive tree search
techniques modern heuristic algorithms quickly converge to
sub-optimal solutions after examining only a small fraction of
the “search space’ and have been successfully applied to
complex optimization problems. Search-based optimization
technique and it involves evolutionary computation.
• It is inspired from Darwinian Theory of evolution. In
evolutionary systems, populations evolve by selective
pressures, mating between individuals, and alterations such as
mutations.
• In genetic algorithms, genetic operators evolve solutions in the

4. METHODOLOGY

5. METHODOLOGY
A genetic algorithm
simulates Darwinian
theory of evolution
using highly parallel,
mathematical
algorithms that,
transform a set
(population) of
solutions (typically
strings of 1's and 0's)
into a new population,
using operators such
as: reproduction,
mutation and
crossover.

6. NUMERICAL EXAMPLE
• Lets start with a simple example, consider the following
equation a +2 b +3 c +4 d = 30. As a solution we have to
determine the values of a,b,c,d that satisfy this equation using
genetic algorithm.
• Objective Function: f (x) = ((a + 2b + 3c + 4d) - 30), our
objective is minimizing the value of function f(x) so as to
satisfy the above equation.
• As to simplify this example, we make a “restriction” that the
values of a,b,c,d would be from the (0 – 30). It will serve as an
initial condition and would simplify the problem to make the
computation speedy and efficient

7. STEP#1| INITIALIZATION
• For initialization, we should have the initial data sets on which
genetic algorithm is to be applied. It is either given or can be
randomly generated.
• We selected the population of 6 chromosomes (individual data-
set). Random values of genes are also selected

8. STEP#2 | EVALUATION
• The values of the given population are put in the objective
function to calculate the individual function.
chromosomes
Genes (values) Objective function
a b c d ((a + 2b + 3c + 4d) - 30
1 12 5 23 8 F_obj[1] 93
2 2 21 18 3 F_obj[2] 80
3 10 4 13 14 F_obj[3] 83
4 20 1 10 6 F_obj[4] 46
5 1 4 13 19 F_obj[5] 94
6 20 5 17 1 F_obj[6] 55

9. STEP#3 | SELECTION
• The fittest chromosome have the highest probability of being
selected for the next generation. Compute fitness probability
by computing fitness of individual chromosome. To avoid the
“divide by zero” problem the value of F_obj is added by 1.
F_obj Values
Fitness ( 1/ (1+
F_obj))
Individual
Probability (P[i] =
Fitness[i] / Total)
cummulative
Probability
F_obj[1] 93 Fitness[1] 0.010638298 P[1] 0.125824361 C[1] 0.125824
F_obj[2] 80 Fitness[2] 0.012345679 P[2] 0.146018394 C[2] 0.271843
F_obj[3] 83 Fitness[3] 0.011904762 p[3] 0.140803452 C[3] 0.412646
F_obj[4] 46 Fitness[4] 0.021276596 P[4] 0.251648722 C[4] 0.664295
F_obj[5] 94 Fitness[5] 0.010526316 P[5] 0.124499894 C[5] 0.788795
F_obj[6] 55 Fitness[6] 0.017857143 p[6] 0.211205177 C[6] 1
Total
0.084548793

10. STEP#3 | CONTINUED
• From the probabilities
calculated in the previous
slide, it can be seen that
chromosome#4 and
chromosome#6 are the fittest
for the next generation. For
the selection process, we use
the roulette wheel.
• The requirement is that the
fittest individuals have a
greater chance of survival than
weaker ones. This replicates
nature in that fitter individuals
will tend to have a better
probability of survival and will
go forward to form the mating
pool for the next generation.

11. STEP#3 | CONTINUED
• We have calculated the
probabilities so that roulette
wheel criterion can be
implemented. It begins by
generating random number R
from 0-1 range.
• For next generation, criterion,
we create R[1] > P[1] & R[1] <
P[2]
then chromosome[2] is
selected
from this criterion, following
new population is
created.chromosome genes
new old a b c d
chromosom
e[1]
chromosom
e[2] 2 21 18 3
chromosom
e[2]
chromosom
e[3] 10 4 13 14
chromosom
e[3]
chromosom
e[1] 12 5 23 8
chromosom
e[4]
chromosom
e[6] 20 5 17 1
chromosom
e[5]
chromosom
e[3] 10 4 13 14
chromosom
e[6]
chromosom
e[4] 20 1 10 6

12. STEP#4 | CROSSOVER
• For crossover techniques, one
cut-point method is employed.
Select a portion in the parent
chromosome then exchanging
sub-chromosome. Parent
chromosome which will mate
is randomly selected and the
number of mate Chromosomes
is controlled using crossover-
rate (ρc) parameters.
• Pseudocode for the cross-over
is as follows:

13. STEP#4 | CONTINUED
• Chromosome K is selected as parent if R[k] < pc, lets suppose pc
= 25% . This means chromosome[k] would be selected for
crossover if R[k] < 0.25
• We have 6 randomly generated data points
• From the given data, chromosome[1,4,5] is
selected for crossover because it meets the
criterion. All 3 combinations for crossover.
• After chromosome selection, the next is the
position of crossover. It is done by generating
random numbers from 1--- ( chromosome length -1)
that is from (1-3)
• Lets suppose C[1] = 1, C[2] = 1, C[3] = 2 are the random numbers
generated from the above criterion. What this means that during
crossover in chromosome 1&2, swapping would be done after first

14. STEP#4 | CONTINUED
New set of chromosome formed after crossover New set of population

15. STEP#5 | MUTATION
• Mutation process is done by
replacing the gene at random
position with a new value. Mutation
rate parameter determines the
mutations in the population
• The process is as follows. Firstly,
calculate the total length of gene in
the population. total
gene = genes in chromosome *
number of population = 4 * 6 =
24
• Mutation process is done by
generating a random integer from (1
to 24). If generated random number
is smaller than mutation rate(ρm)
define ρm 10%, it is expected that
10% (0.1) of total gene in the
population that will be mutated
• number of mutations = 0.1 * 24 =
2.4 ≈ 2
• Suppose generation of random
number yield 12 and 18 which
corresponds to mutation in
chromosome 3 gene4 and
Chromosome 5 gen number 2. The
value of mutated gens at mutation
point is replaced by random number
between 0-30. Suppose generated
random number are 2 and 5 then
Chromosome composition after

16. ITERATION
• Finishing mutation process then we have one iteration or one
generation of the genetic algorithm. We can now evaluate the
objective function after one generation:
• As can be seen, clearly the objective and fitness function has
improved. This process is continued until best or desirable results
are achieved. For our case after 50 iterations
• Chromosome = [07; 05; 03; 01] This means that: a = 7, b = 5, c = 3,
d = 1 If we use the number in the problem equation a +2 b +3 c +4
chromosomes
genes objective function
a b c d ((a +2b+3c+4d)-30)
1 2 5 17 1 37
2 10 4 13 14 83
3 12 5 23 2 69
4 20 4 13 14 93
5 10 5 18 3 56
6 20 1 10 6 46