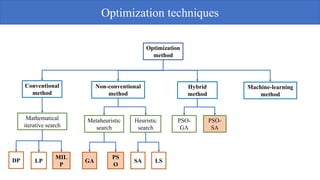
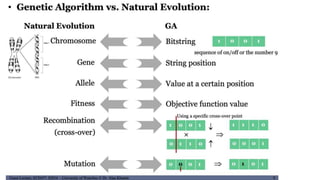
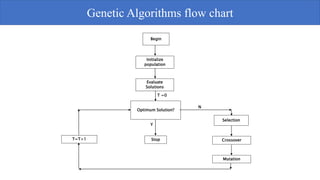
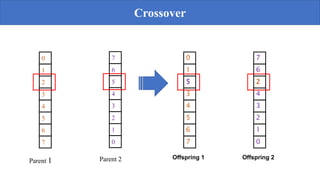
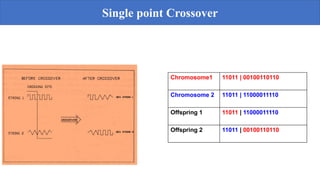
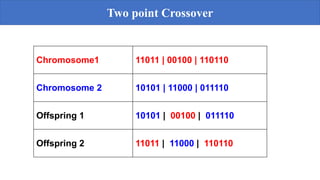
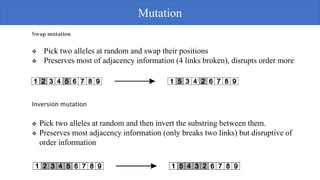
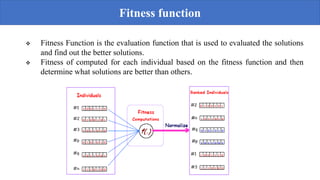
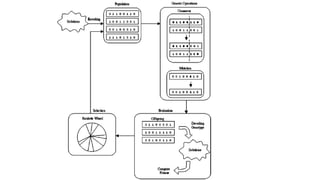
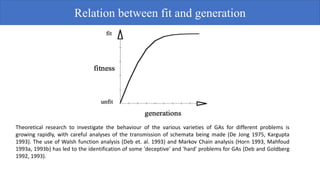
Genetic algorithms are a probabilistic search algorithm that iteratively transforms a population of potential solutions into a new generation using Darwinian principles of natural selection and genetic operations like crossover and mutation. John Holland developed the original genetic algorithm in the 1970s using binary representations, selection proportional to fitness, and crossover and mutation to produce new individuals. Genetic algorithms represent potential solutions as strings and evolve the population through generations to arrive at an optimal solution.

1. Genetic algorithm

2. Optimization
method
Conventional
method
Hybrid
method
Machine-learning
method
Non-conventional
method
MIL
P
LP
Metaheuristic
search
Mathematical
iterative search
PSO-
GA
DP
Heuristic
search
PSO-
SA
GA
PS
O
SA LS
Optimization techniques

3. Genetic Algorithms
Definition:
The genetic algorithm is a probabilistic search algorithm that iteratively
transforms a set (called a population) of mathematical objects (typically fixed-
length binary character strings), each with an associated fitness value, into a new
population of offspring objects using the Darwinian principle of natural
selection and using operations that are patterned after naturally occurring genetic
operations, such as crossover (recombination) and mutation.
Developed by John Holland, University of Michigan (1970’s):
The original form of the GA, as illustrated by John Holland in 1975 had distinct
features: a bit string representation, proportional selection and cross-over to
produce new individuals.

5. Genetic Algorithms

6. Begin
Initialize
population
Optimum Solution?
T=T+1
Selection
Crossover
Mutation
N
Evaluate
Solutions
Y
Stop
T =0
Genetic Algorithms flow chart

7. Parent 1 Parent 2
0
1
5
3
5
4
7
6
7
6
2
4
2
3
0
1
0
1
2
3
5
4
7
6
7
6
5
4
2
3
0
1
Offspring 1 Offspring 2
Crossover

8. Chromosome1 11011 | 00100110110
Chromosome 2 11011 | 11000011110
Offspring 1 11011 | 11000011110
Offspring 2 11011 | 00100110110
Single point Crossover

9. Chromosome1 11011 | 00100 | 110110
Chromosome 2 10101 | 11000 | 011110
Offspring 1 10101 | 00100 | 011110
Offspring 2 11011 | 11000 | 110110
Two point Crossover

10.  Assign 'heads' to one parent, 'tails' to the other
 Flip a coin for each gene of the first child
 Make an inverse copy of the gene for the second child
 Inheritance
Uniform Crossover

11.  Mutation introduces randomness into the population.
 Why ‘Mutation’
The idea of mutation is to reintroduce divergence into a
converging population.
 Mutation is performed on small part of population,
 in order to avoid entering unstable state.
1 1 0 1 0 10 0
0 1 0 1 0 10 1
1 0
0 1
Parent
Child
Mutation

12. Swap mutation
 Pick two alleles at random and swap their positions
 Preserves most of adjacency information (4 links broken), disrupts order more
Inversion mutation
 Pick two alleles at random and then invert the substring between them.
 Preserves most adjacency information (only breaks two links) but disruptive of
order information
Mutation

13.  Fitness Function is the evaluation function that is used to evaluated the solutions
and find out the better solutions.
 Fitness of computed for each individual based on the fitness function and then
determine what solutions are better than others.
Fitness function

14.  The selection operation copies a single individual, probabilistically
selected based on fitness, into the next generation of the population.
 Several possible ways
 Keep the strongest
 Keep some of the weaker solutions
Survival of The Strongest
0.93 0.51 0.72 0.31 0.12 0.64Previous generation
Next generation
0.93 0.72 0.64
Selection

15. Chance to be selected as parent proportional to fitness
Roulette wheel
To avoid problems with fitness function
Tournament
As the name suggests tournaments are played between two
solutions and the better solution is chosen and placed in the
mating pool.
Parent selection

17.  Individual - Any possible solution
 Population - Group of all individuals
 Search Space - All possible solutions to the problem
 Chromosome - Blueprint for an individual
 Trait - Possible aspect (features) of an individual
 Allele - Possible settings of trait (black, blond, etc.)
 Locus - The position of a gene on the chromosome
 Genome - Collection of all chromosomes for an individual
Genetic Algorithms main terminology

18. Genetic algorithms differ from traditional algorithms in four
ways (Goldberg, 1989):
1. GAs usually work with a coding of the parameter set, not the parameters
themselves.
2. GAs search from a population of points, not a single point.
3. GAs use payoff (objective function) information, not derivatives or other
auxiliary knowledge.
4. GAs use probabilistic transition rules, not deterministic rules.

19. Theoretical research to investigate the behaviour of the various varieties of GAs for different problems is
growing rapidly, with careful analyses of the transmission of schemata being made (De Jong 1975, Kargupta
1993). The use of Walsh function analysis (Deb et. al. 1993) and Markov Chain analysis (Horn 1993, Mahfoud
1993a, 1993b) has led to the identification of some 'deceptive' and 'hard' problems for GAs (Deb and Goldberg
1992, 1993).
Relation between fit and generation

20.  Parallel GAs, where multiple processors are used in parallel to run the GA (Adeli and Cheng 1994, Levine
1994).
 Distributed GAs, where multiple populations are separately evolved with few interactions between them
(Whitley and Starkweather 1990)
 GAs with niching and speciation, where the population within the GA is segregated into separate 'species'
(Horn 1993, Horn and Nafpliotis 1993, Horn et. al. 1994).
 Messy GAs (mGA), which use a number of 'exotic' techniques such as variablelength chromosomes and a
two-stage evolution process (Deb 1991, Deb and Goldberg, 1991).
 Multiobjective GAs (MOGAs), which allow multiple objectives to be optimised with GAs (Schaffer 1985,
Srinivas and Deb 1995, Bentley and Wakefield 1997).
 Hybrid GAs (hGAs), where GAs are combined with local search algorithms (George 1994, Radcliffe and
Surrey 1994a).
 Structured GAs (sGAs), which allow parts of chromosomes to be switched on and off using evolveable
'control genes' (Dasgupta and McGregor 1992, Parmee and Denham 1994).
 GAs with diploidy and dominance, which can improve variation and diversity in addition to performance
(Smith & Goldberg, 1992b).
 Mutation-driven GAs, such as Harvey's SAGA (Harvey, 1997), which uses converged populations modified
primarily by mutation to allow the constant 'incremental evolution' of new solutions to varying fitness
functions.

21. Machine learning (Goldberg 1989, Goldberg et. al. 1992b, Holland 1992,
Smith and Goldberg 1992a, Horn et. al. 1994).
Strategy acquisition (Greffenstette, 1991).
Ordering problems (Kargupta et al. 1992, Schaffer & Eshelman 1995).
Control systems (Husbands et al. 1996).
Fault-tolerant systems (Thompson, 1995).
Scheduling (Yamada and Nakano, 1995).
Data mining (Radcliffe and Surrey 1994b).
Set covering and partitioning (Levine 1994).
Signal timing (Foy et. al., 1992).
Composition of music (Horner and Goldberg, 1991)
Evolution of engineering designs (Bentley & Wakefield, 1996a,b)
Some Applications of Genetic Algorithms

22. Adaptive antenna arrays and radar absorbers (Chambers et. al., 1995).
Airfoil and aircraft geometries (Husbands, Jermy, McIlhagga, & Ives 1996).
Analogue filters (Reeves et al., 1994).
Building heating systems (Dickinson and Bradshaw, 1995).
Floorplans (Koakutsu et al., 1992).
Sizes of gas pipes (Boyd, 1994).
Hydraulic networks (Donne et al., 1994).
Microwave absorbing materials (Tennant and Chambers, 1994).
Satellite Booms (Keane and Brown, 1996).
Servo and micro motors (Hameyer and Belmans, 1996).
Spacecraft systems (Garipov et. al., 1994).
Structural topology (Rozvany and Zhou 1994).
Transmission towers (Cai and Thierauf, 1996).
VLSI layouts (Schnecke and Vornberger 1995).
GAs have been used to optimize