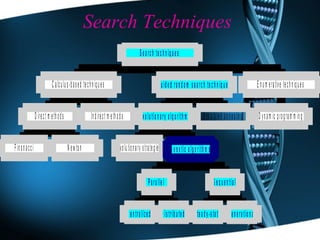
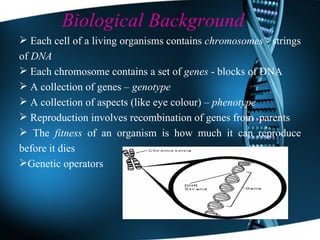
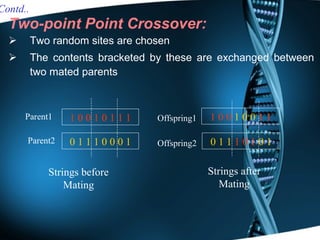
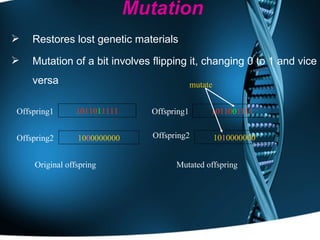
Genetic algorithms are optimization techniques inspired by Darwin's theory of evolution. They use operations like selection, crossover and mutation to evolve solutions to problems by iteratively trying random variations. The document outlines the history, concepts, process and applications of genetic algorithms, including using them to optimize engineering design, routing, computer games and more. It describes how genetic algorithms encode potential solutions and use fitness functions to guide the evolution toward better outcomes.

1. Genetic Algorithms Presentation By: Divya Rani R, Fazeelath Naziya

5. Search Techniques

10. Simple Genetic Algorithm Step 1: Encoding of the problem in a binary string Step 2: Random generation of a population Step 3: Calculate fitness of each solution Step 4: S elect pairs of parent strings based on fitness Step 5: Generate new string with crossover and mutation until a new population has been produced Repeat step 2 to 5 until satisfying solution is obtained

12. Permutation Encoding – Every chromosome is a string of numbers, which represents the number in the sequence. Used in ordering problems. Ex: Traveling Sales Person Problem Encoding: Chromosome represents the order of cities, in which the salesman will visit them Contd.. 8 5 6 7 2 3 1 4 9 Chromosome B 1 5 3 2 6 4 7 9 8 Chromosome A

13. Value Encoding – Every chromosome is a string of some values. Values can be form numbers, real numbers or characters. Ex: Finding weights for neural network The problem : To find the weights of synapses connecting input to hidden layer and hidden layer to output layer Encoding: Each value chromosome represent the corresponding weights Contd.. Chromosome A 1.2324 5.3243 0.4556 2.3293 2.4545 Chromosome B ABDJEIFJDHDIERJFDLDFLFEGT Chromosome C (back), (back), (right), (forward), (left)

18. Contd.. 100.0 1170 Total 30.9 361 10011 4 5.5 64 01000 3 49.2 576 11000 2 14.4 169 01101 1 % Of Total Fitness String No.

39. Conclusion Genetic algorithms are original systems based on the supposed functioning of the Living. The method is very different from classical optimization algorithms. These algorithms are nevertheless extremely efficient, and are used in many fields.

41. Thank You