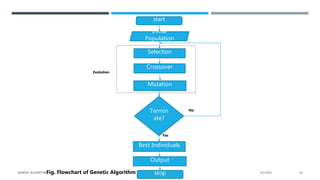
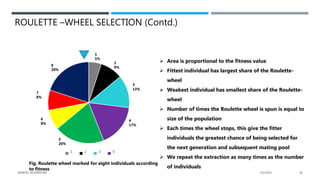
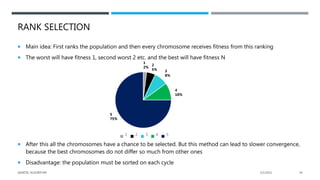
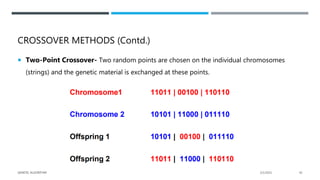
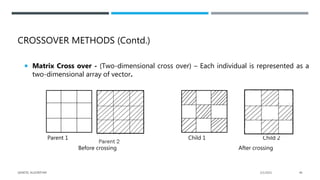
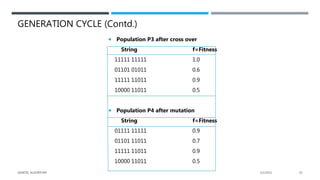
The document presents a comprehensive overview of genetic algorithms (GAs), which are search-based optimization techniques inspired by the principles of natural selection and genetics. It outlines their history, key concepts, and components including fitness functions, selection methods, crossover techniques, and the mapping of biological processes to computational problems. Additionally, it highlights the advantages and limitations of GAs, making them suitable for solving complex optimization problems.