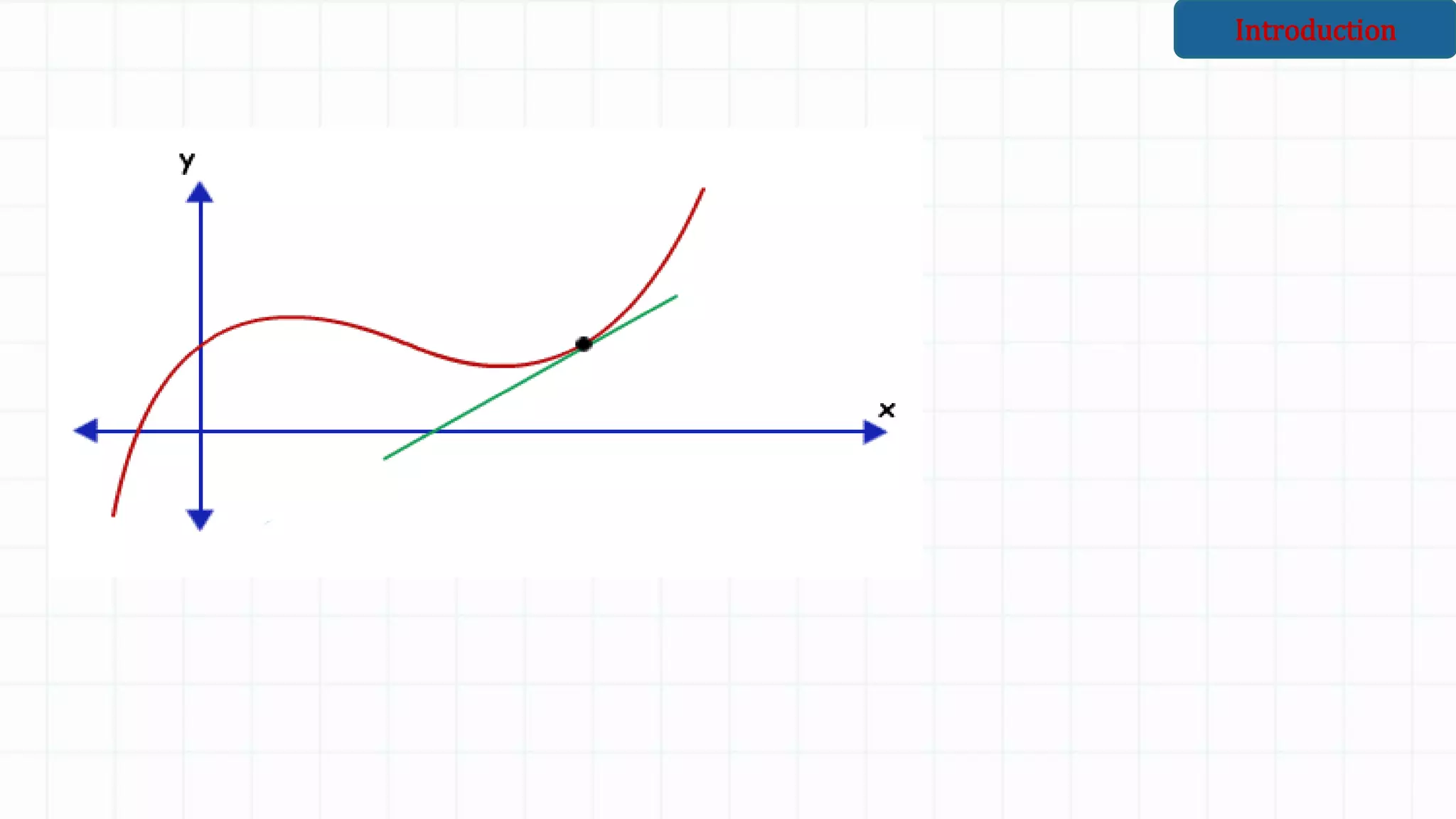
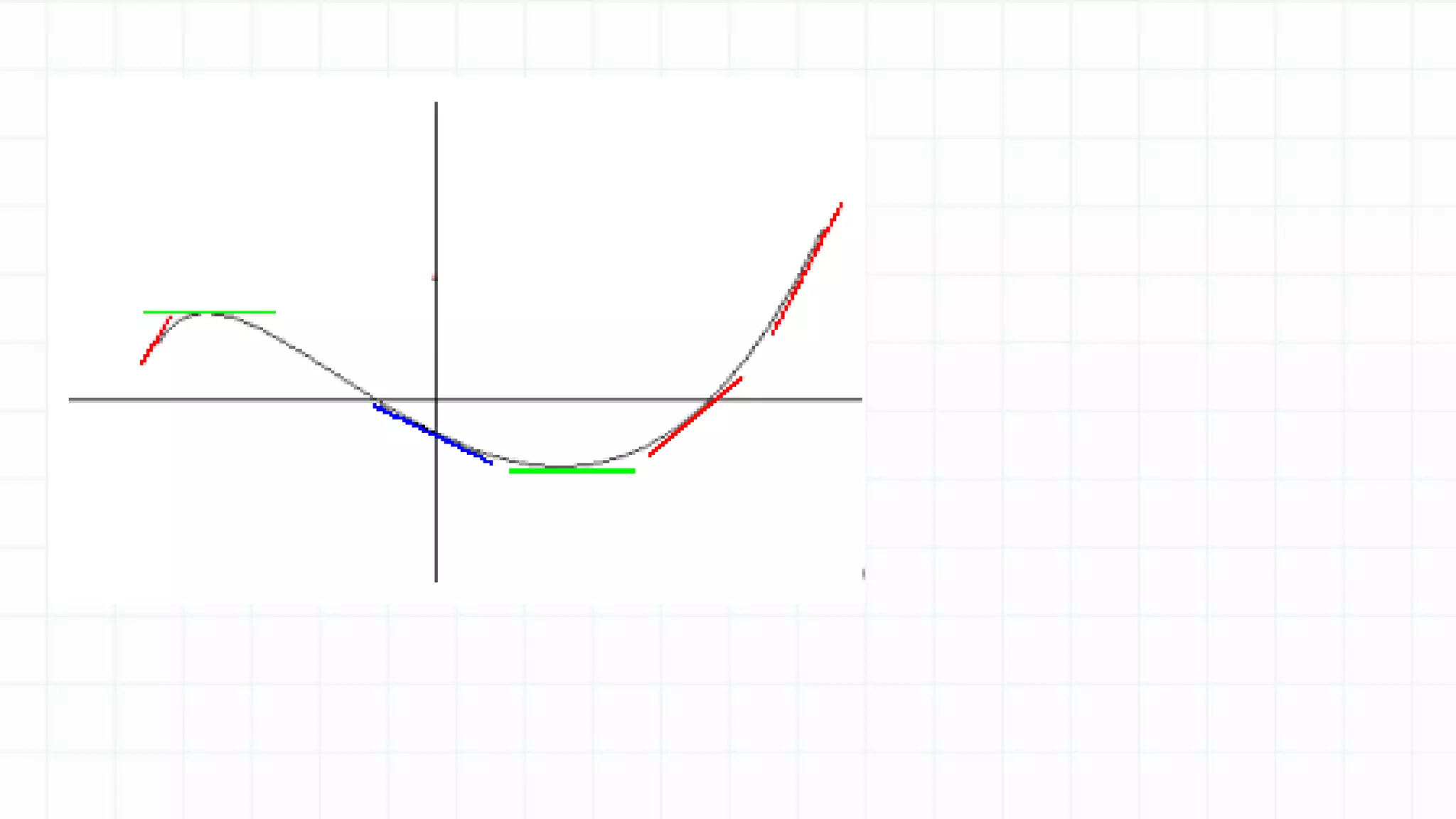
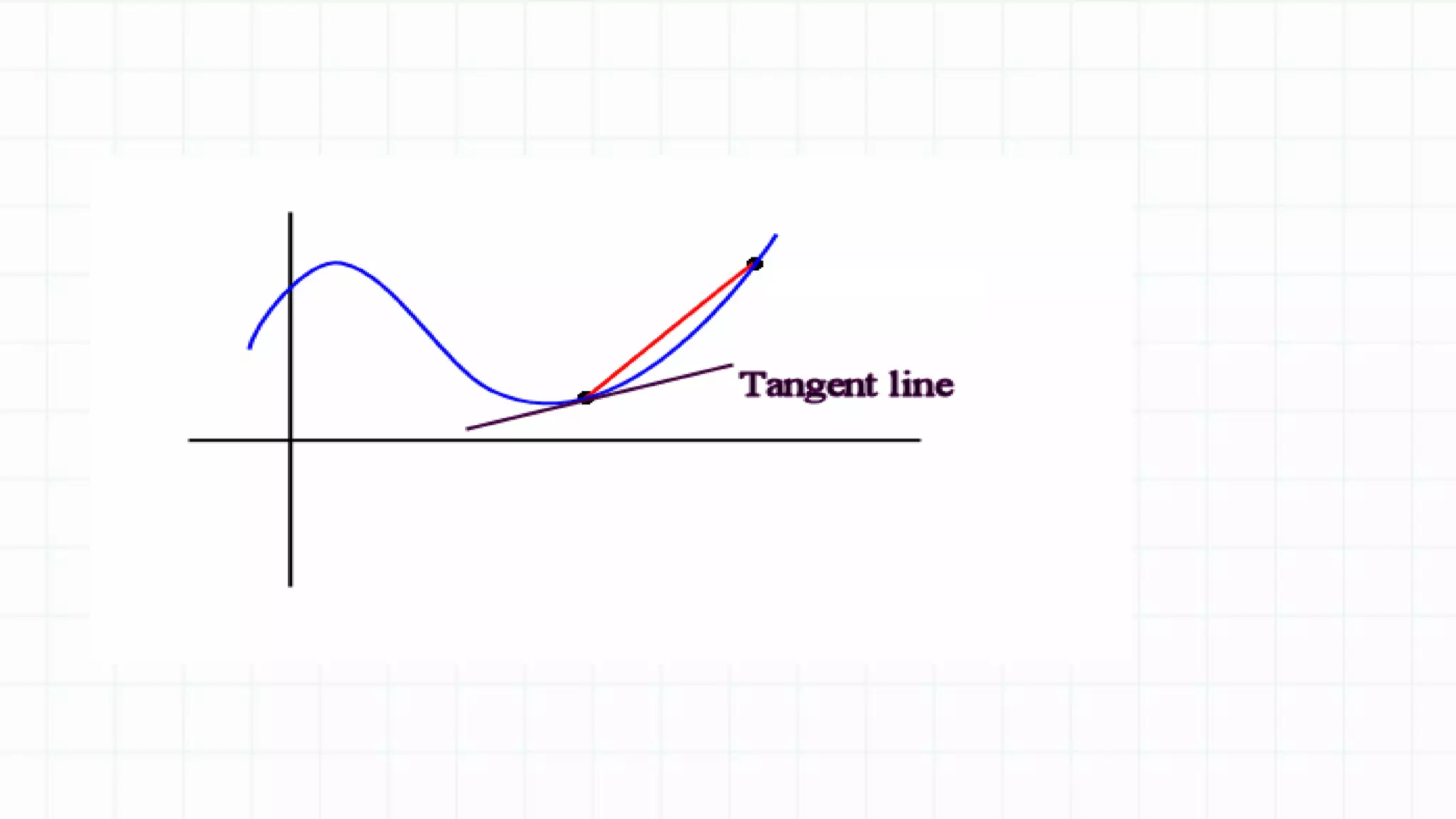
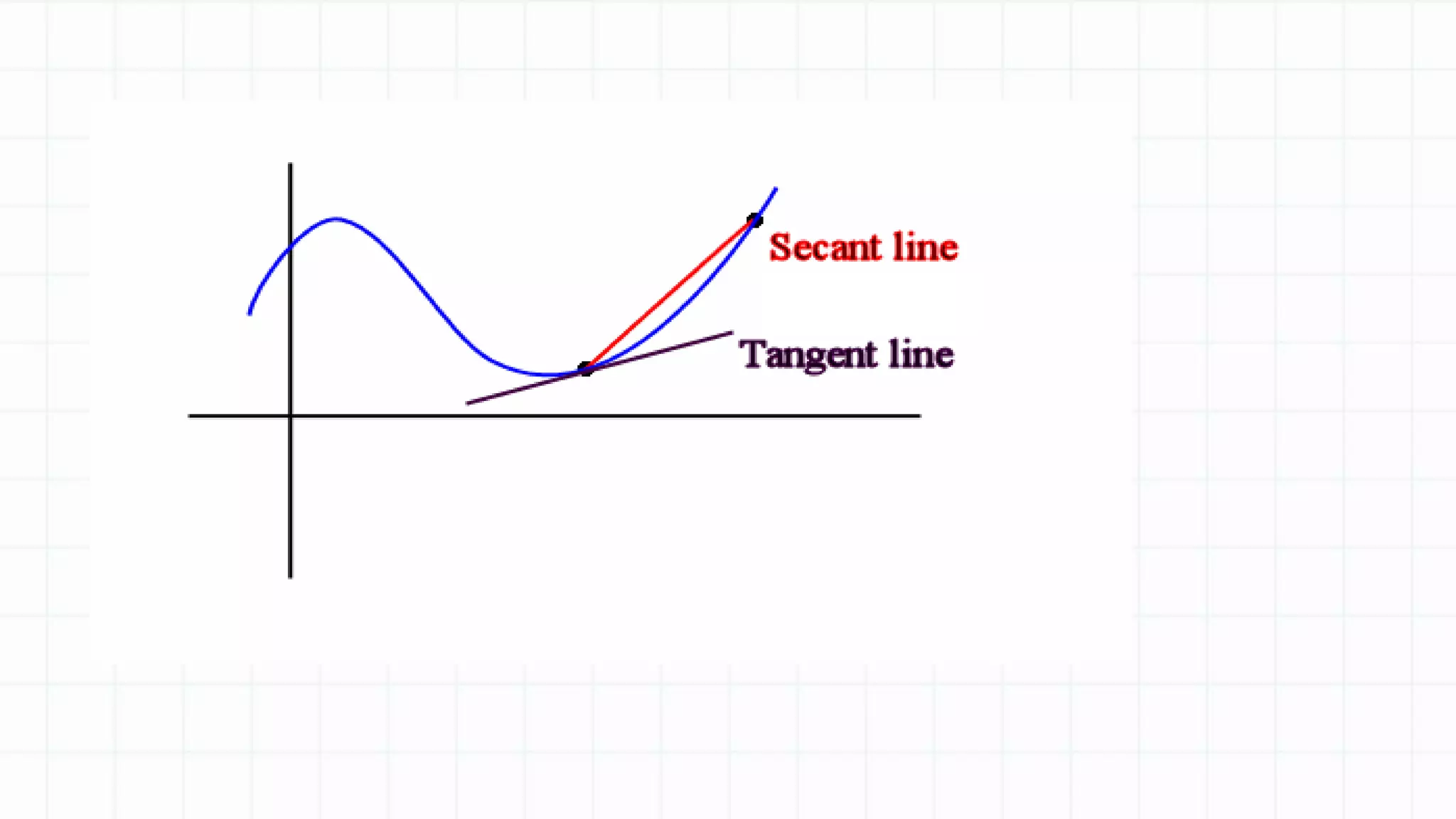
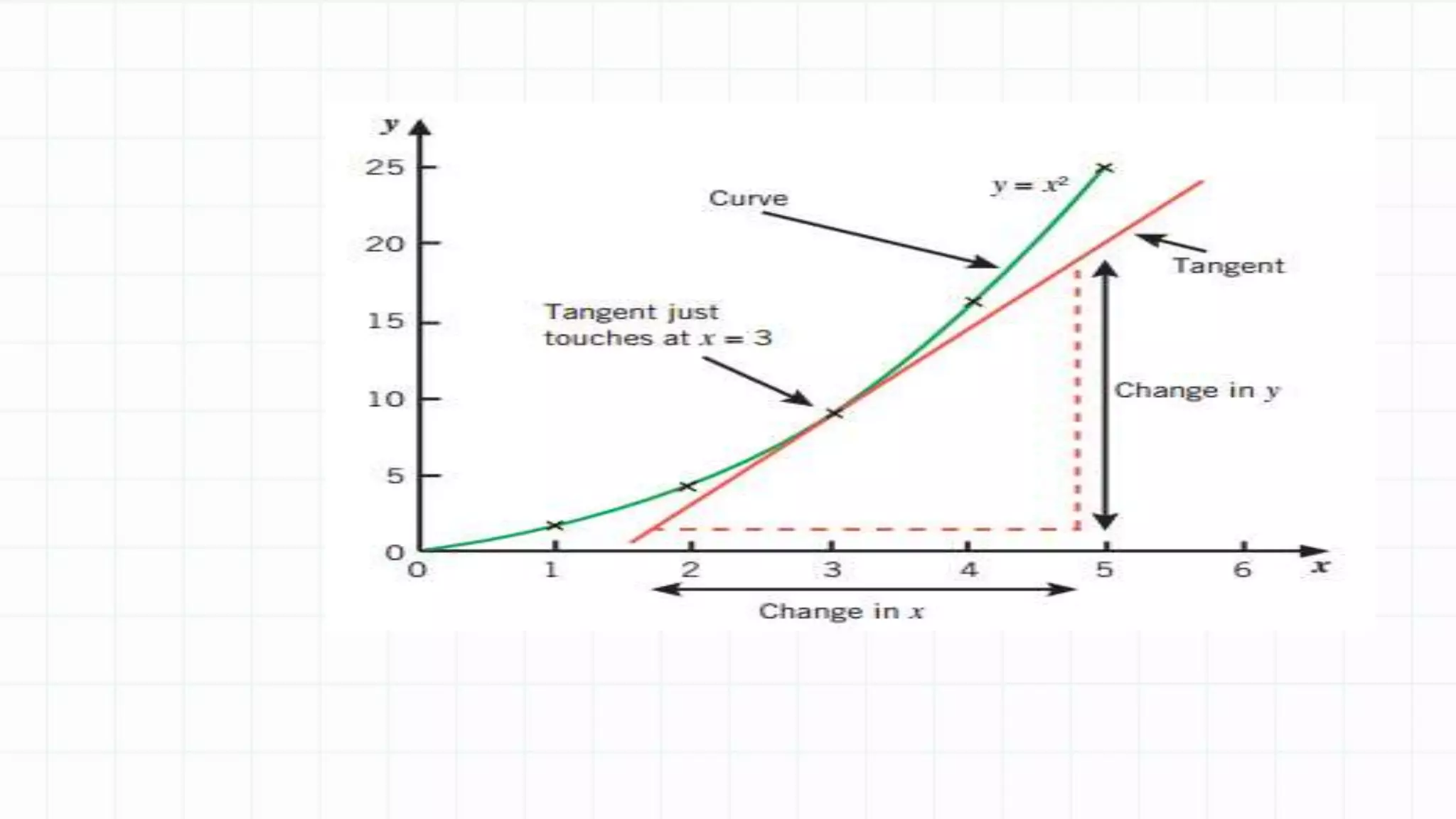
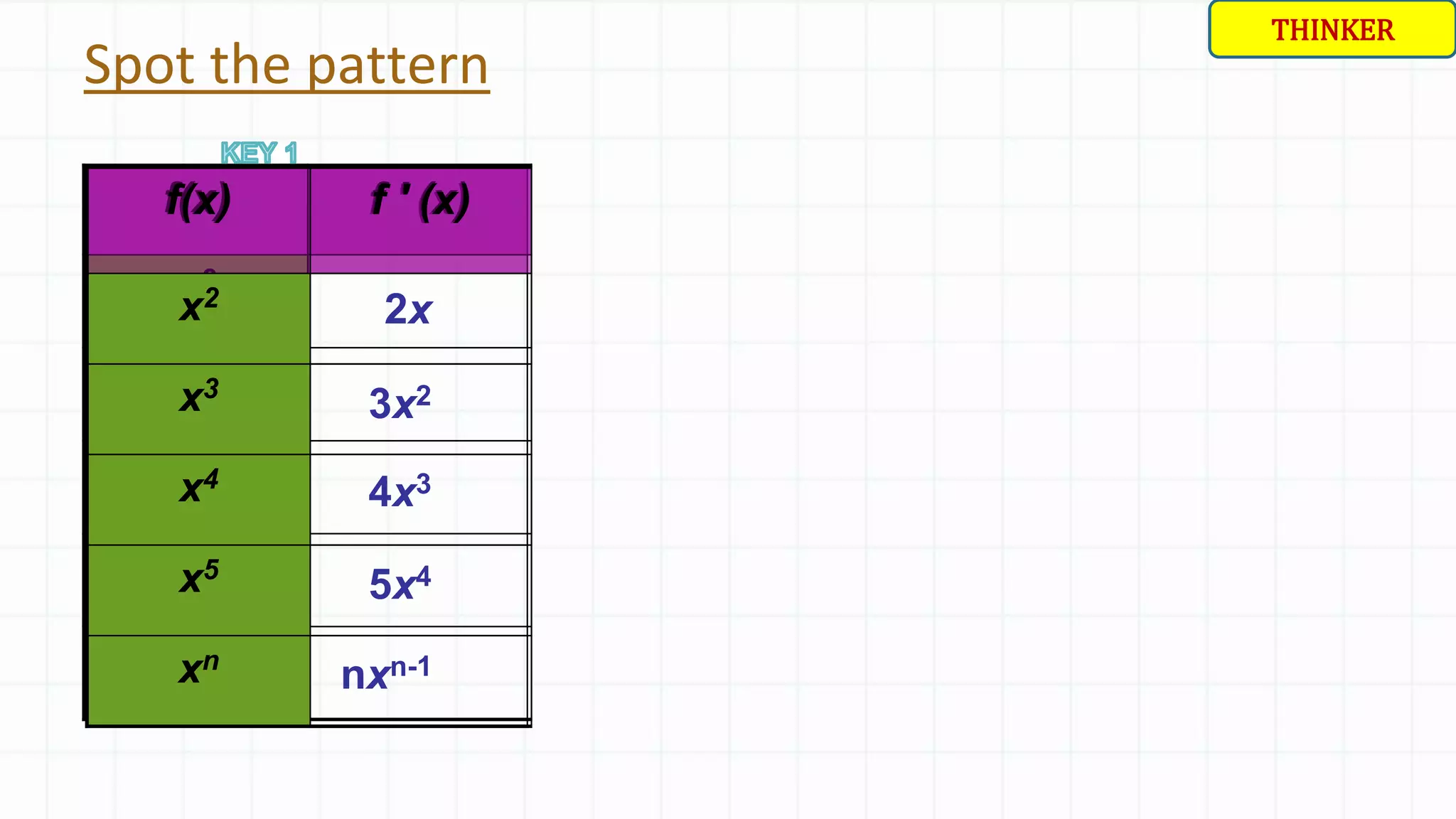
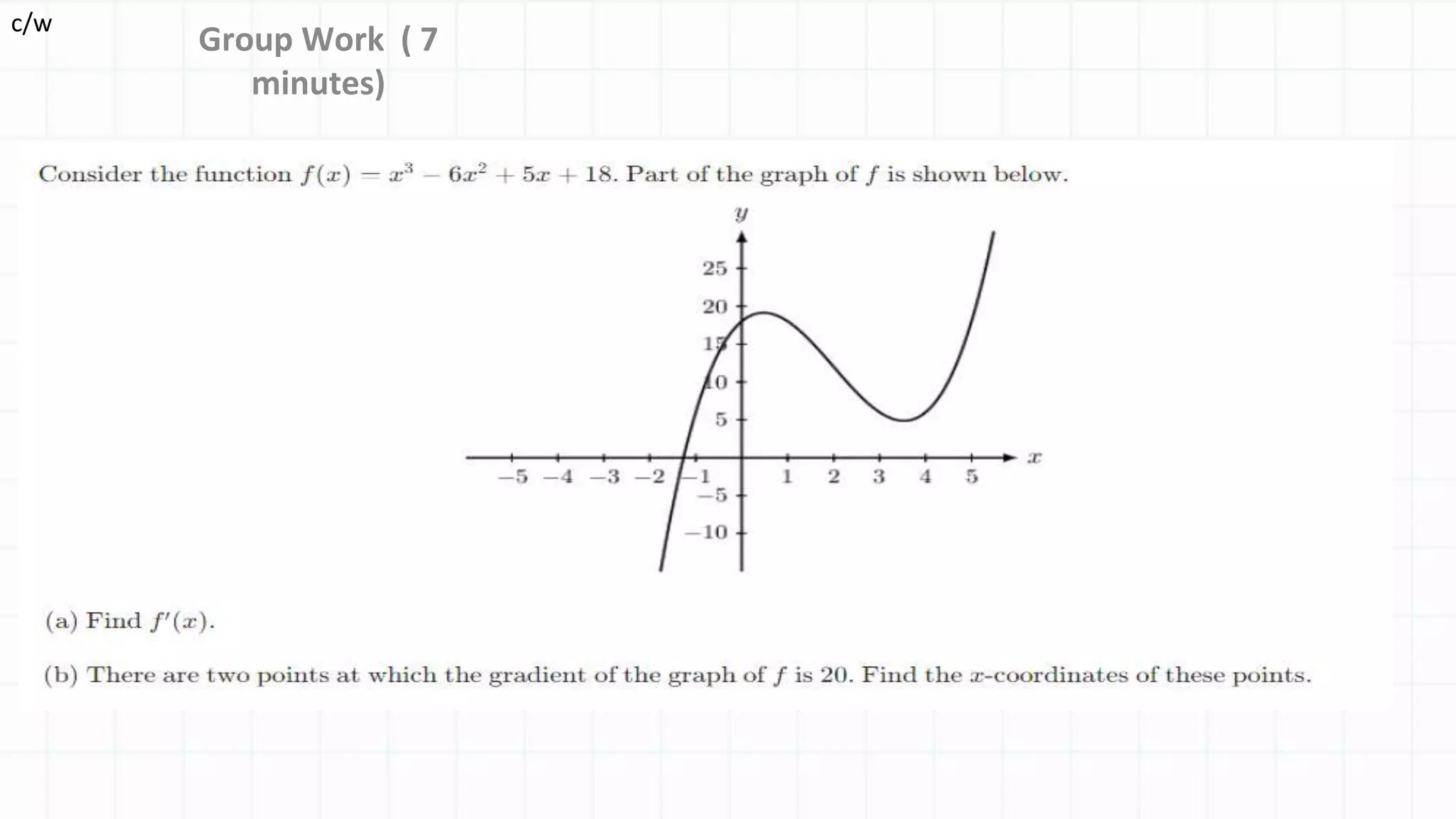
The document discusses differentiation and finding the derivative of functions. It begins with lesson objectives of understanding how differentiation can be used to find the gradient of a curve and learning the basic rules of differentiation. It then defines differentiation as finding the gradient function, also called the derivative. Several examples are provided to illustrate the pattern for finding the derivative of functions like x^2, x^3, etc. The basic rules of differentiation are outlined, including how to take the derivative of sums and constant functions. Students are then instructed to practice applying these rules through examples.

1. STARTER
If Y = 4x 5 + 12 x 2 + 2x and x = 5. Find the value of Y.
12810
Fastest Fingers!!! 4 minutes

2. STARTER
https://www.transum.org/Software/SW/Starter_of_the_day
/starter_March16.ASP
Coins the tables!!! 4 minutes

3. Date: 05-03-2023
UNIT 12:
Analyzing Rates of CHANGE: Differential calculus
INQUIRER THINKER KNOWLEDGEABLE COMMUNICATOR ASSESSMENT REFLECTION
PRINCIPLED
FEEDBACK HOTS
TOPIC: Differentiation PAGE NO: 522- 545

4. Lesson Objectives
 To Understand the application of Differentiation in
finding the gradient of a curve.
 To understand the rules of Differentiation.

5. Pair Work
Research ( 5 Minutes)
RATE OF CHANGE
Gradient of curve
Relationship between rate rate of
change and gradient of curve

6. Introduction

11. Lesson Objectives
 To Understand the application of Differentiation in
finding the gradient of a curve.
 To understand the rules of Differentiation.

12. DIFFERENTIATION
▪ It is the algebraic process used to find the gradient
function of any given function.
▪ The gradient function is called the Derivative.

13. Notation
The most common notations are:
The derivative of a function f(x) with respect to x is defined as f’(x).
 Leibnitz notation used for f’(x) is dy
dx

14. f(x) f ′ (x)
x2
x3
x4
x5
xn
Spot the pattern
f(x) f ′ (x)
x2
x3
x4
x5
xn
f(x) f ′ (x)
x2
x3
x4
x5
xn
2x
3x2
4x3
5x4
nxn-1
THINKER

15. Rule of thumb:
▪ Multiply by the power and reduce the power by 1.

16. f(x) f ′ (x)
2x2
3x2
4x2
5x2
ax2
Spot the pattern
f(x) f ′ (x)
2x2
3x2
4x2
5x2
ax2
f(x) f ′ (x)
2x2
3x2
4x2
5x2
ax2
4x
6x
8x
10x
2ax
THINKER

17. Rules for differentiation
There are 4 rules for differentiating – remember these and you
can differentiate anything …
Rule Examples
1. f(x) = x6  f ′ (x) =
2.
f(x)= 4x3  f ′ (x) =
3. f(x) = 65  f ′ (x) =
f(x) = g(x) + h(x)
 f ′ (x) = g′ (x) + h′ (x)
f(x)= x6 + 4x2 + 65  f ′ (x) =
6 x 6 - 1 = 6 x 5
4 x 3 x 3-1
= 12 x 2 or 12 x 2
0
6 x 5 + 8x

18. ▪
APPLY YOUR
Knowledge

19. https://www.transum.org/software/SW/Starter_of_the_day/Students/Dif
ferentiation.asp

20. Group Work ( 7
minutes)
c/w

21. 25/10/2021
c/w

22. Check your understanding – page 509 - 510
25/10/2021
c/w
Question 2
Question 5
Question 6