Uploaded byPratima Nayak ,Kendriya Vidyalaya Sangathan
Introduction to coordinate geometry by pratima nayak
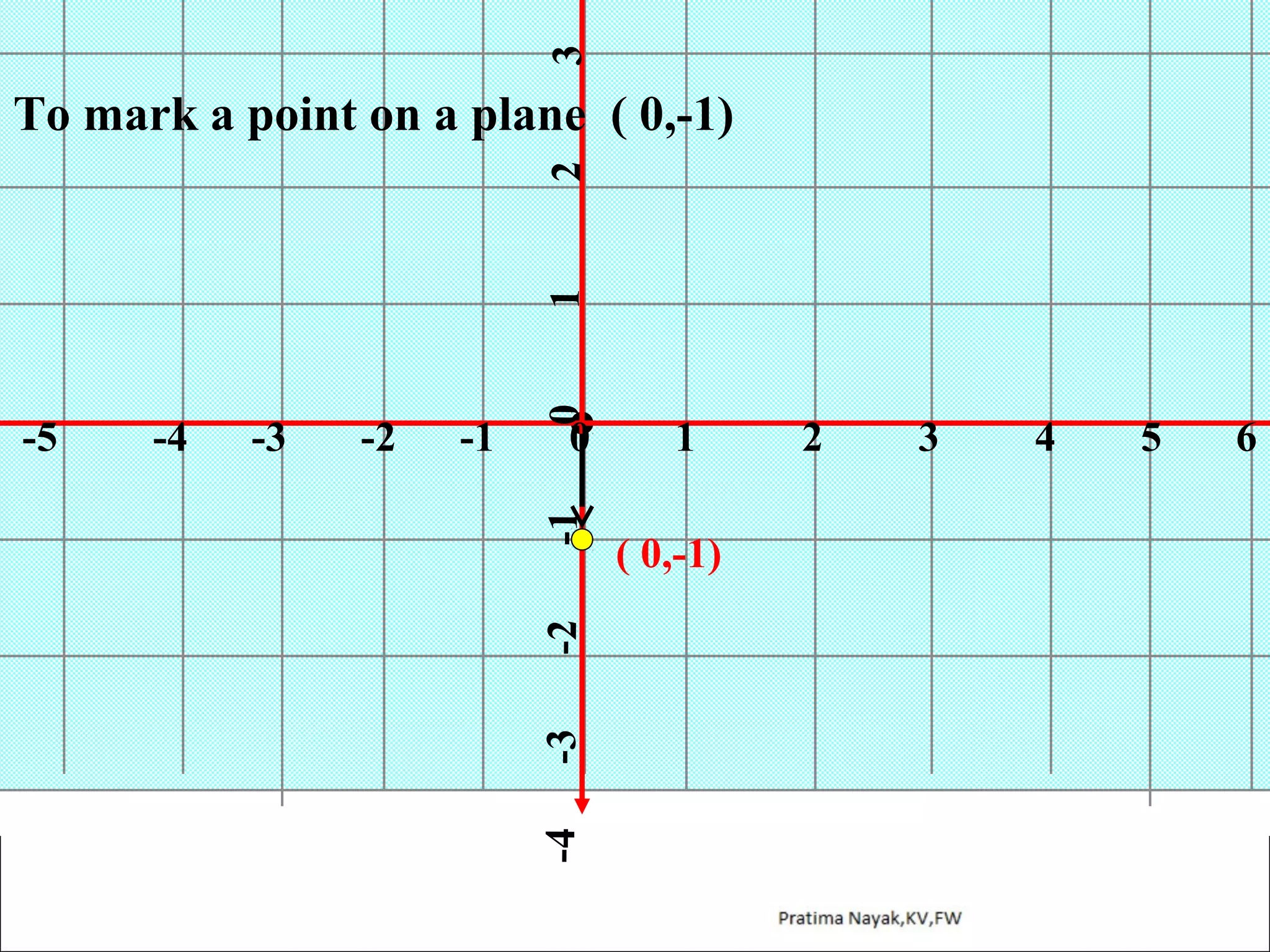
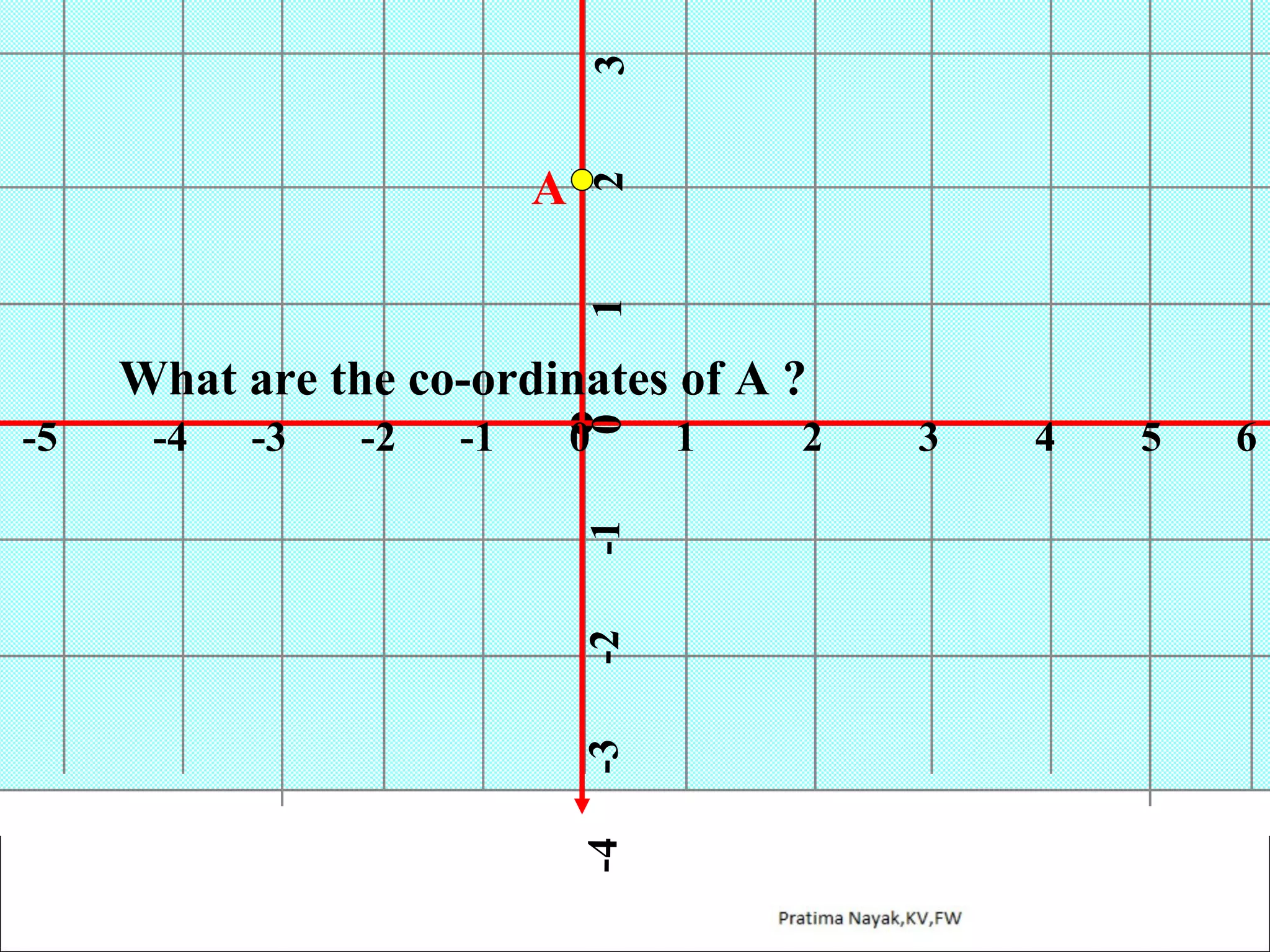
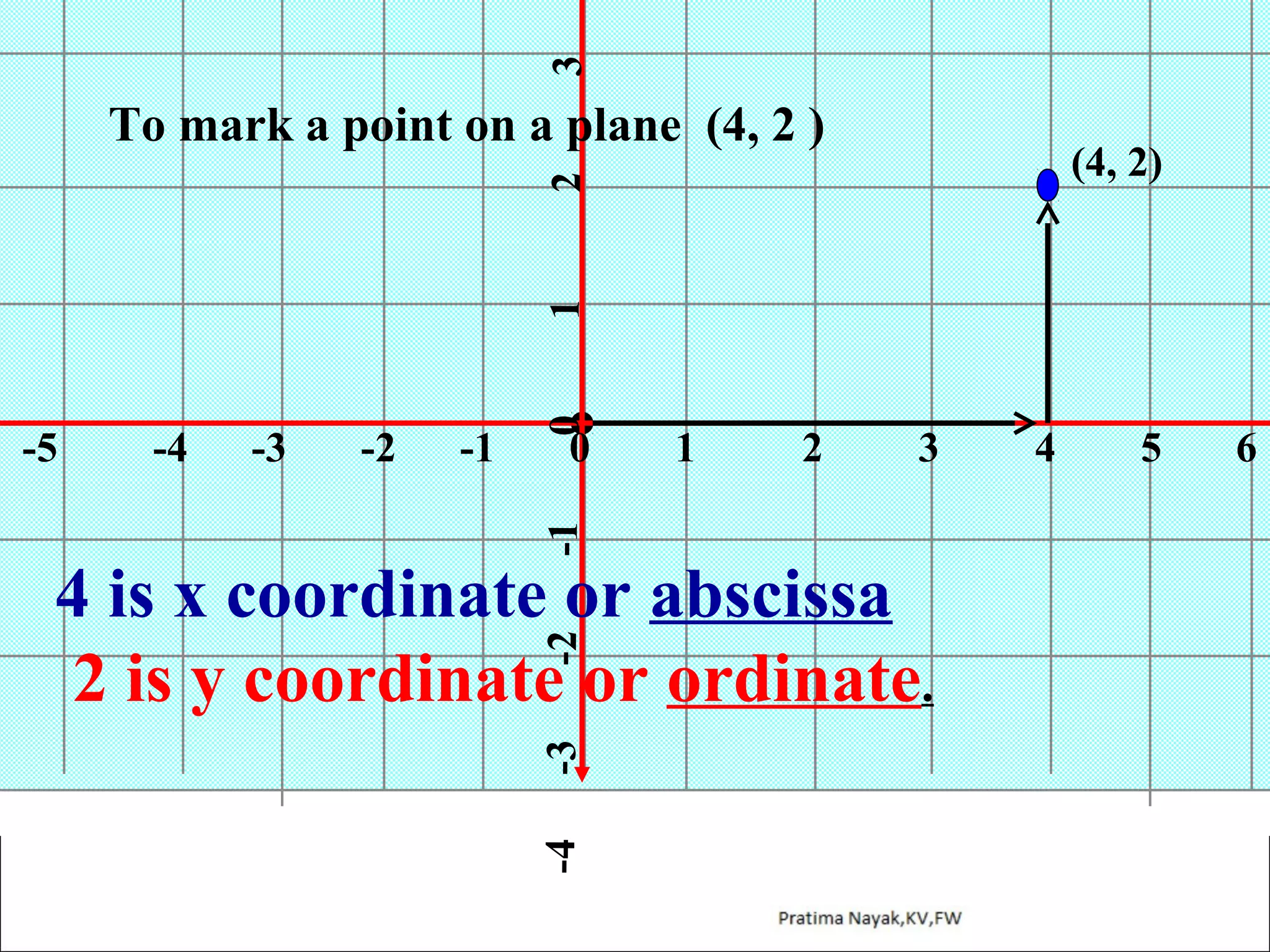
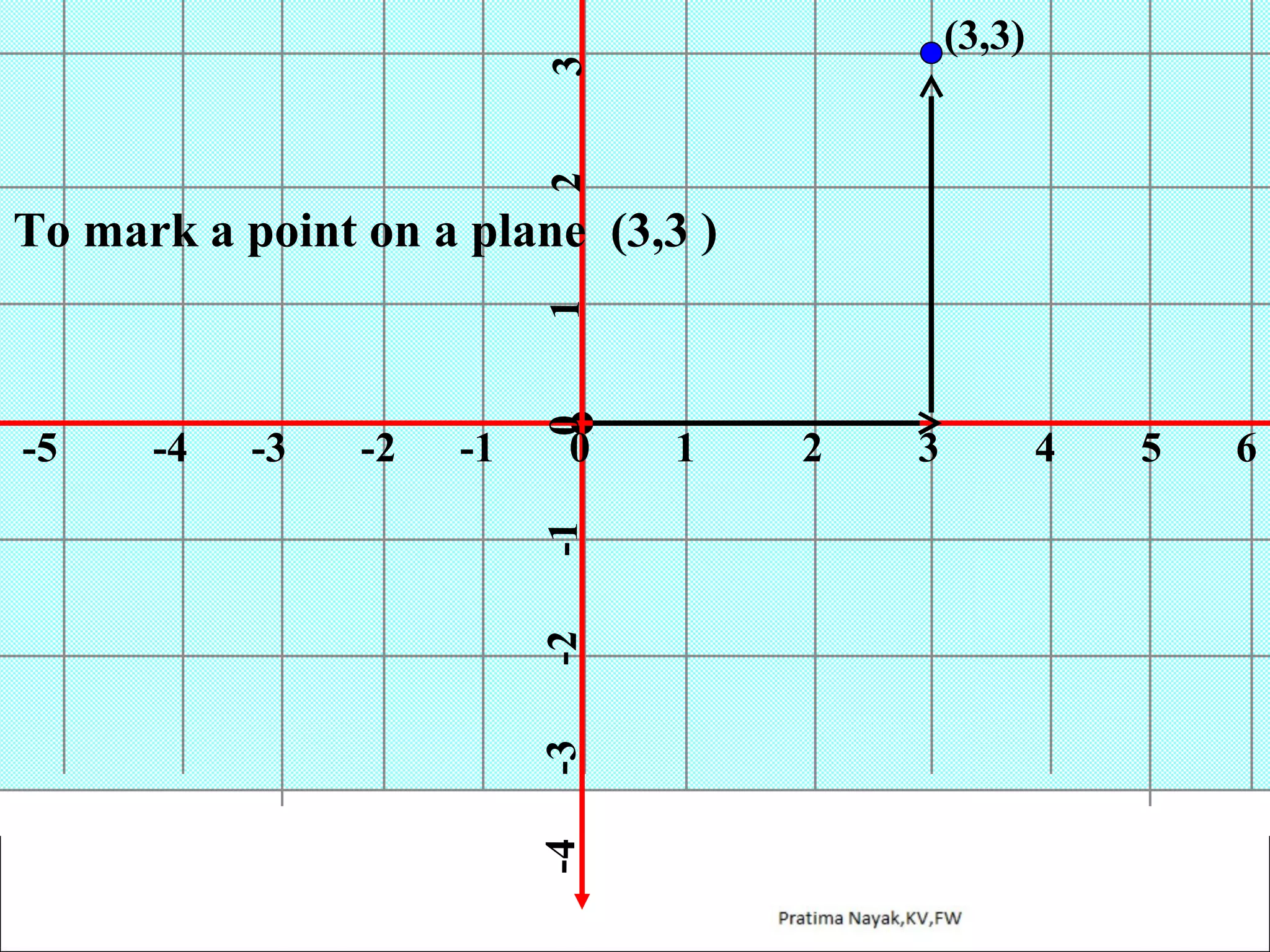
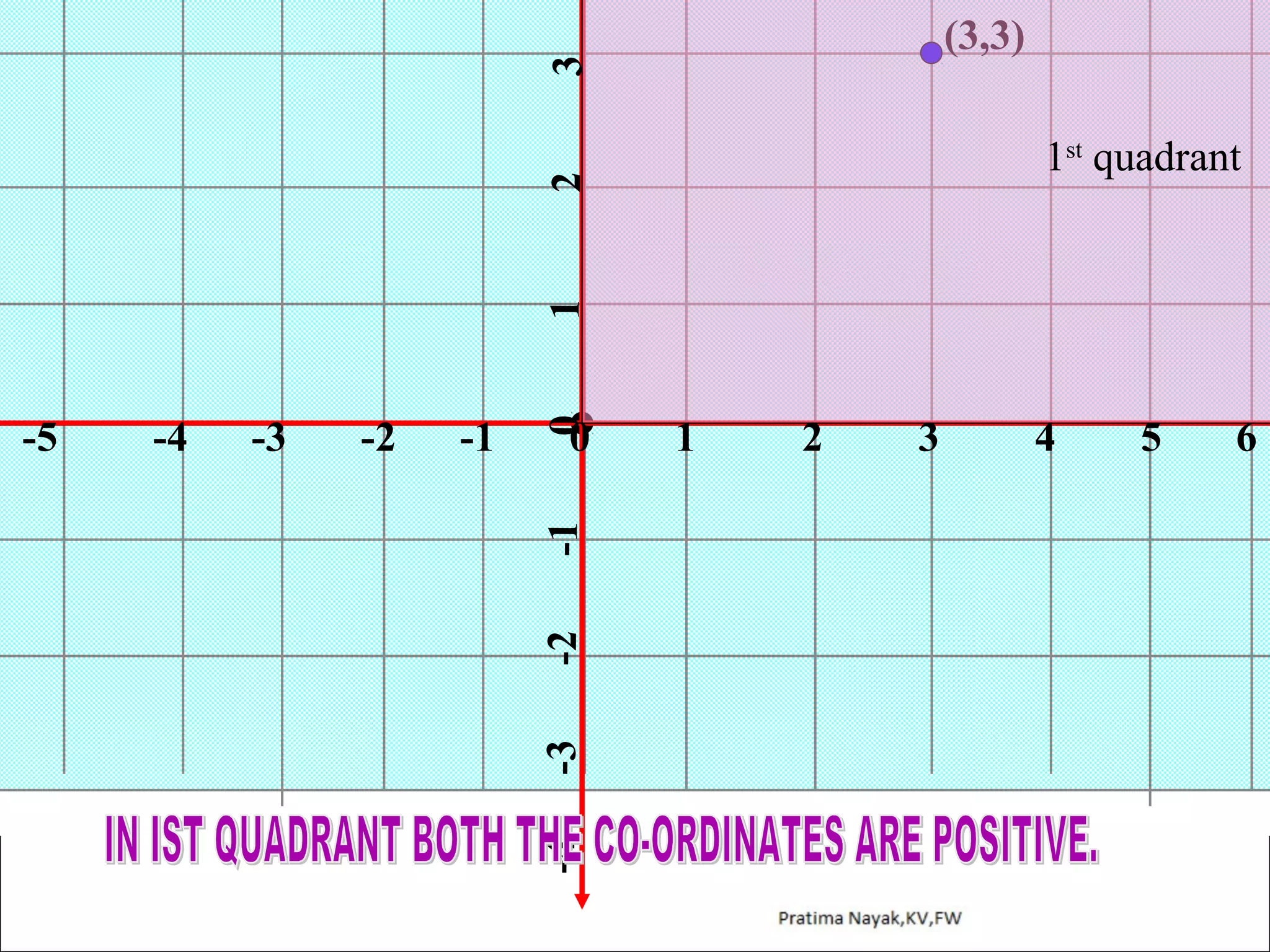
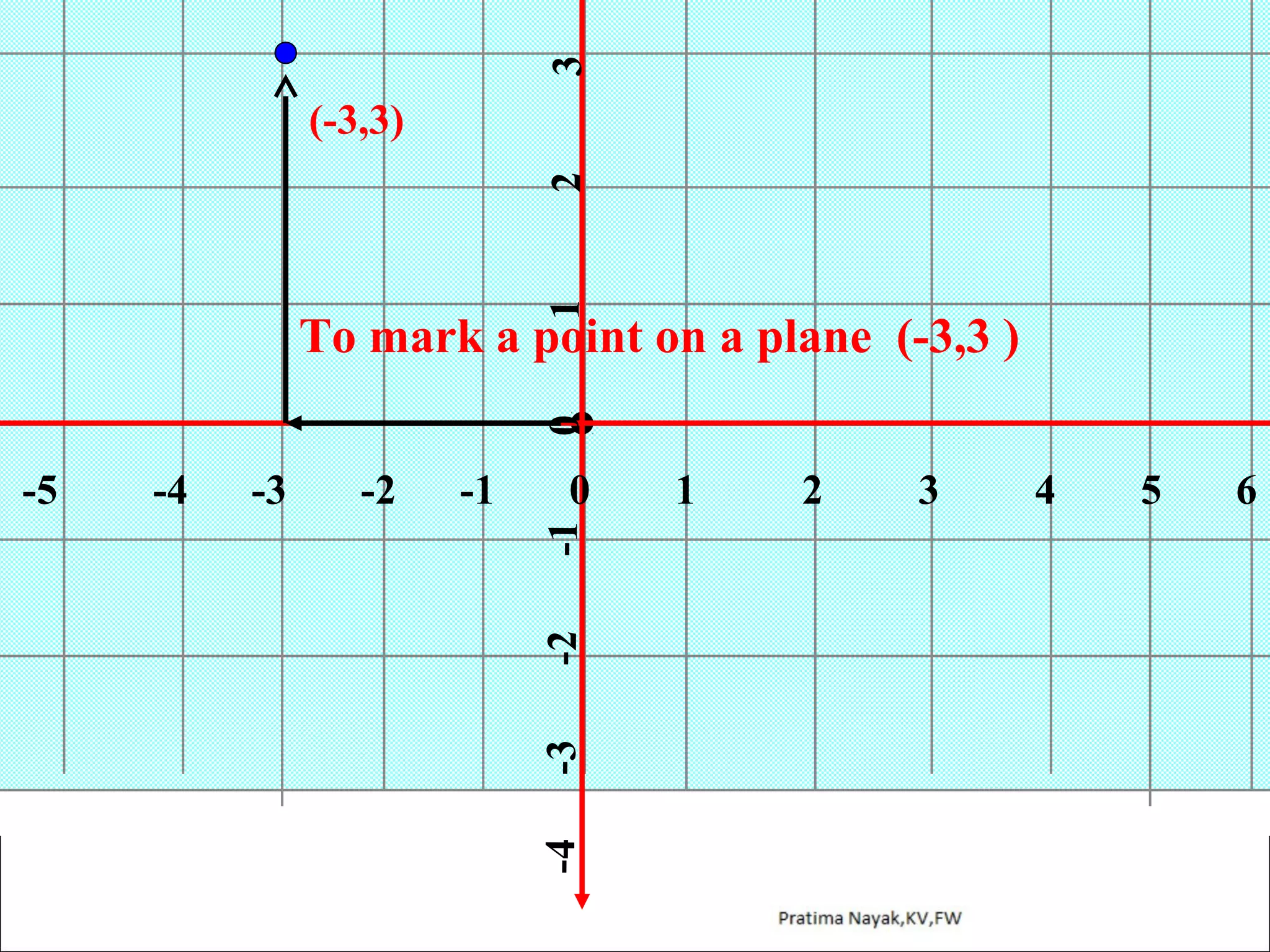
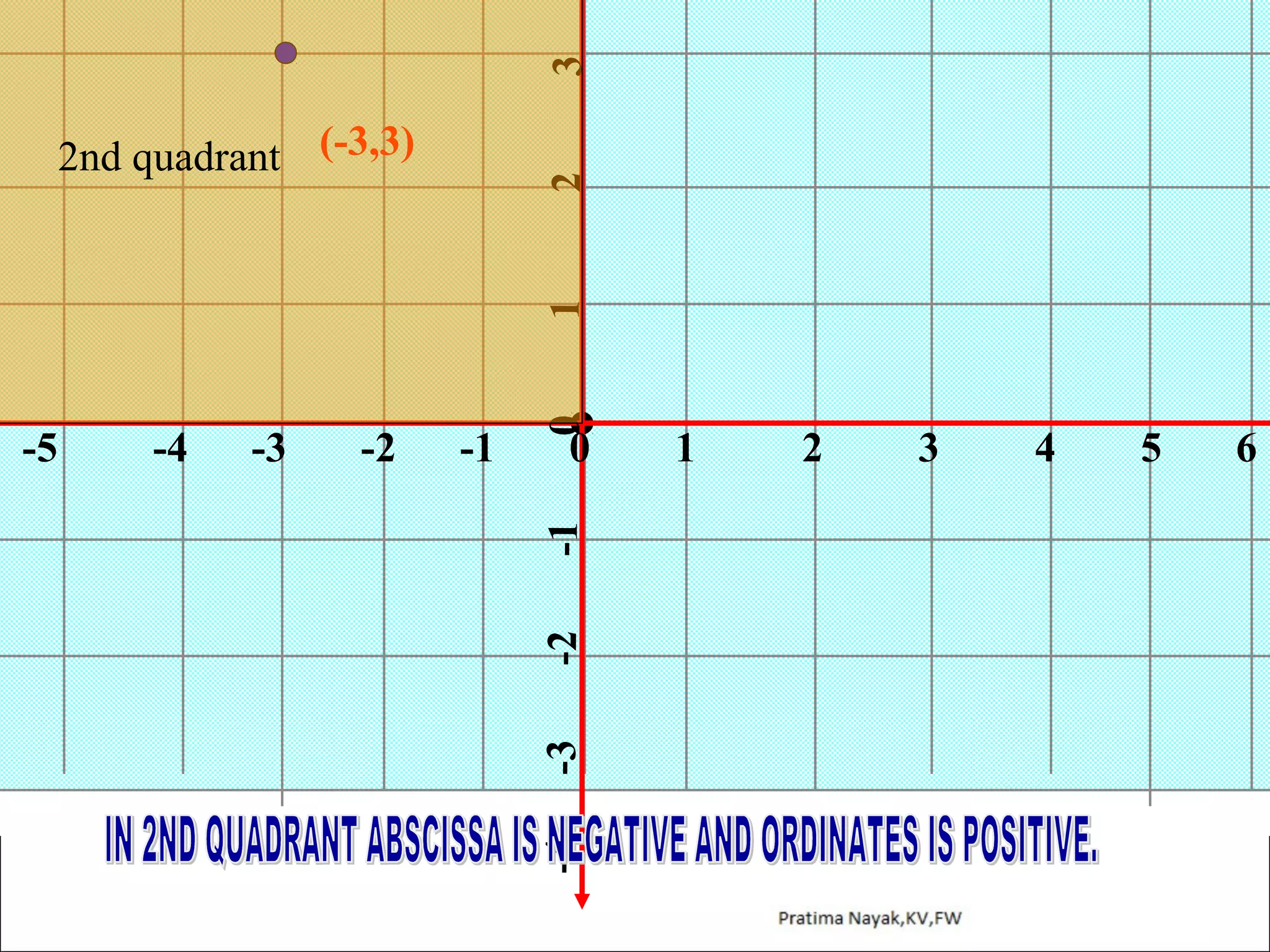
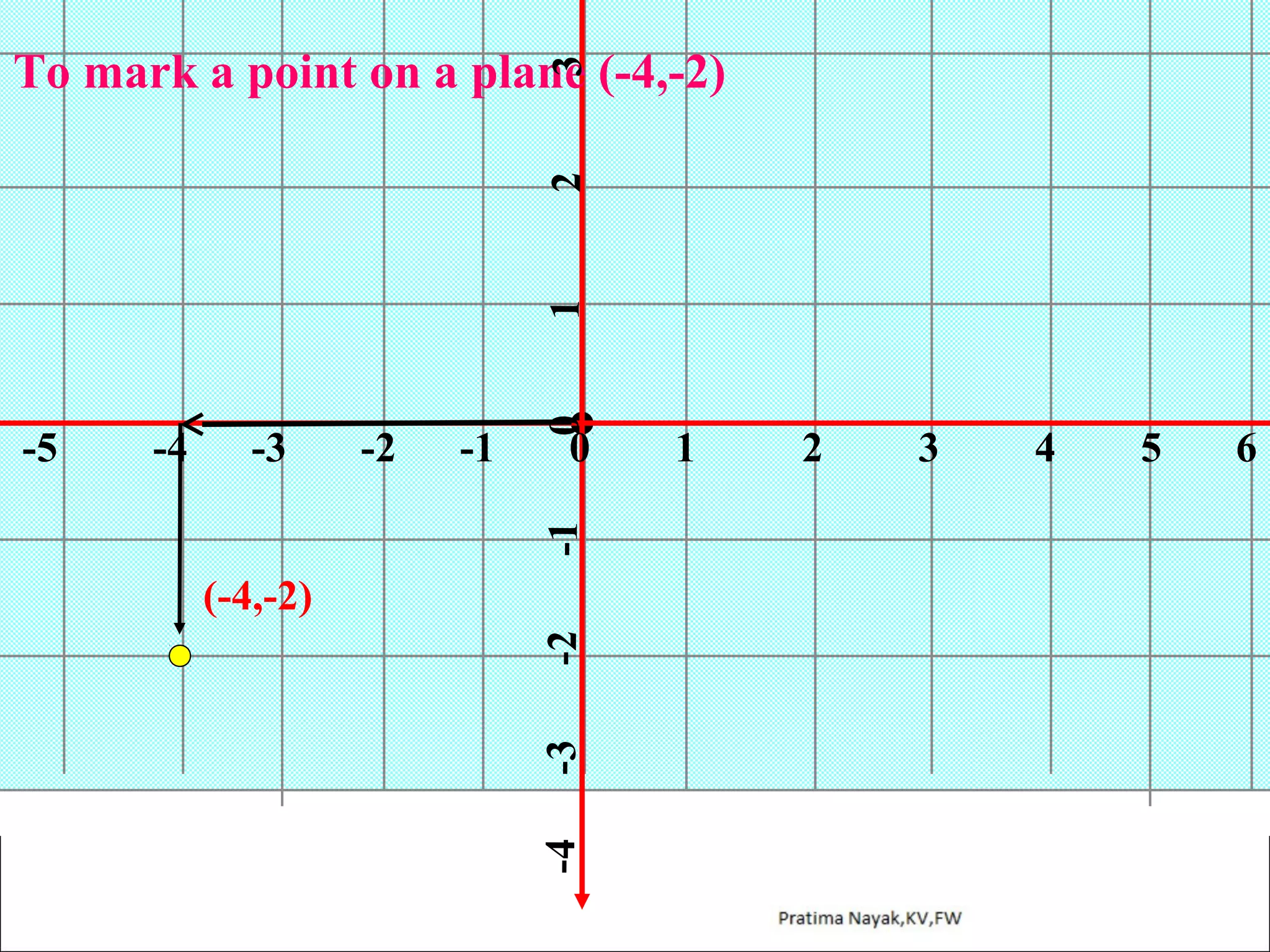
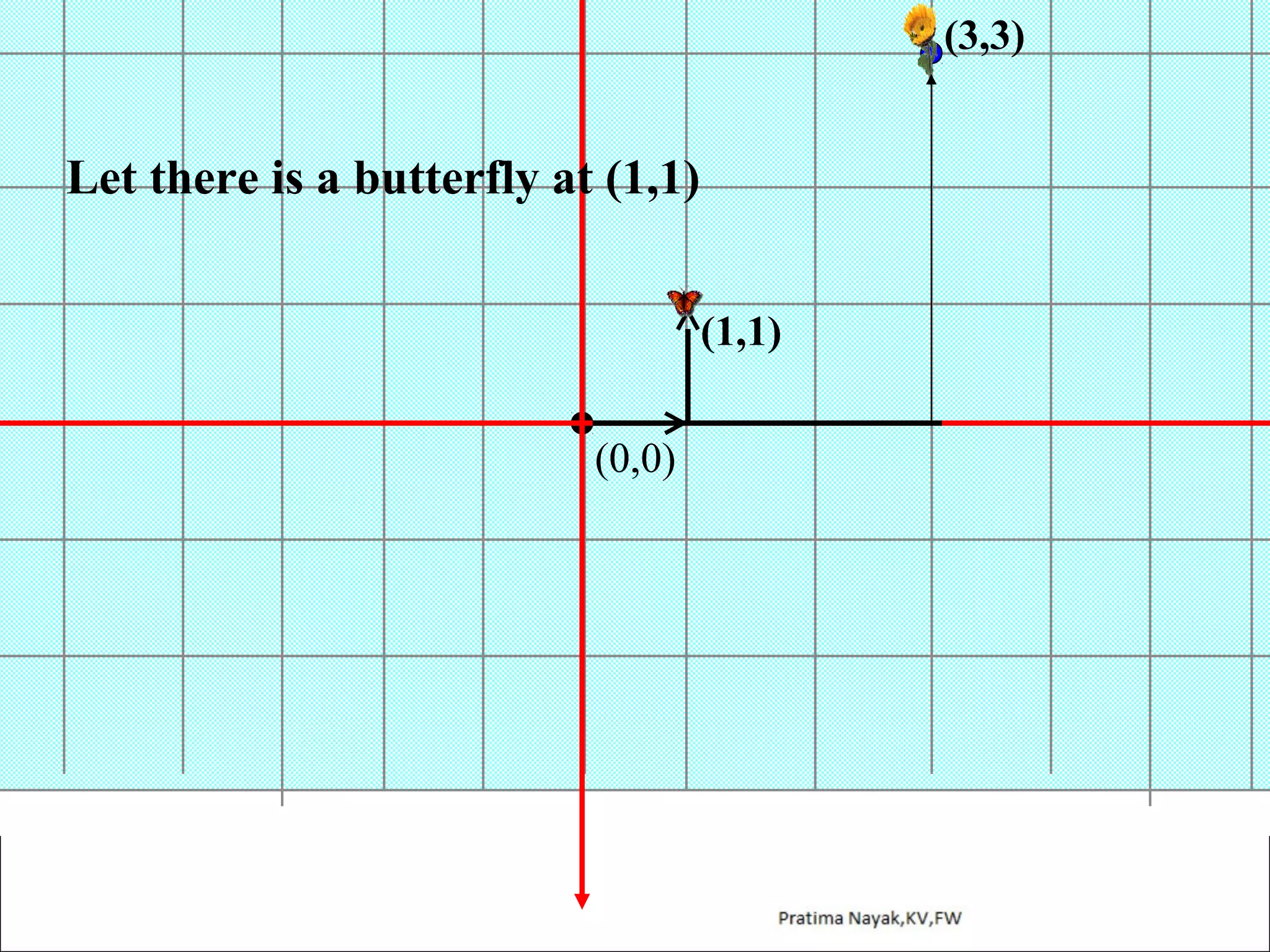
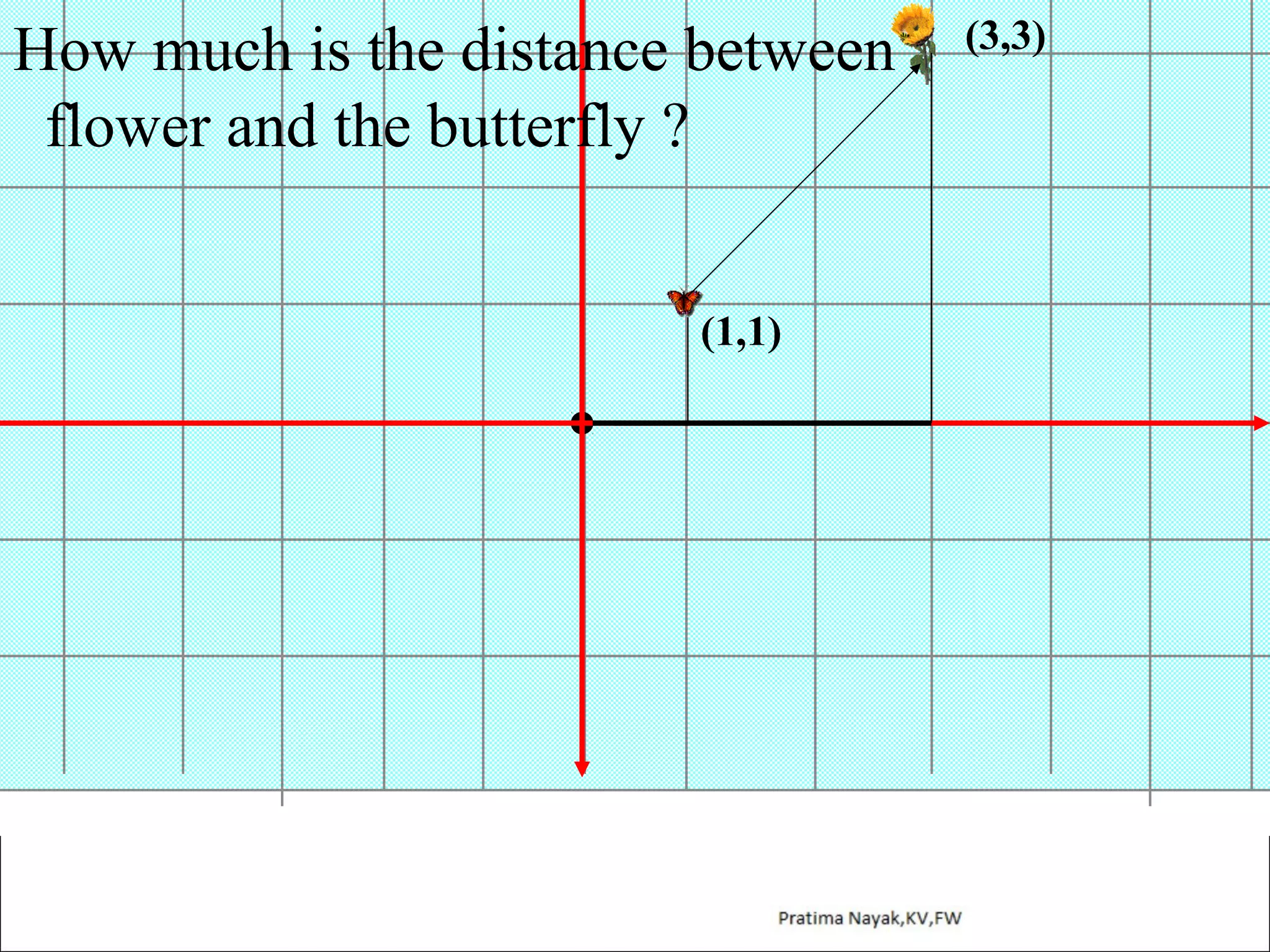
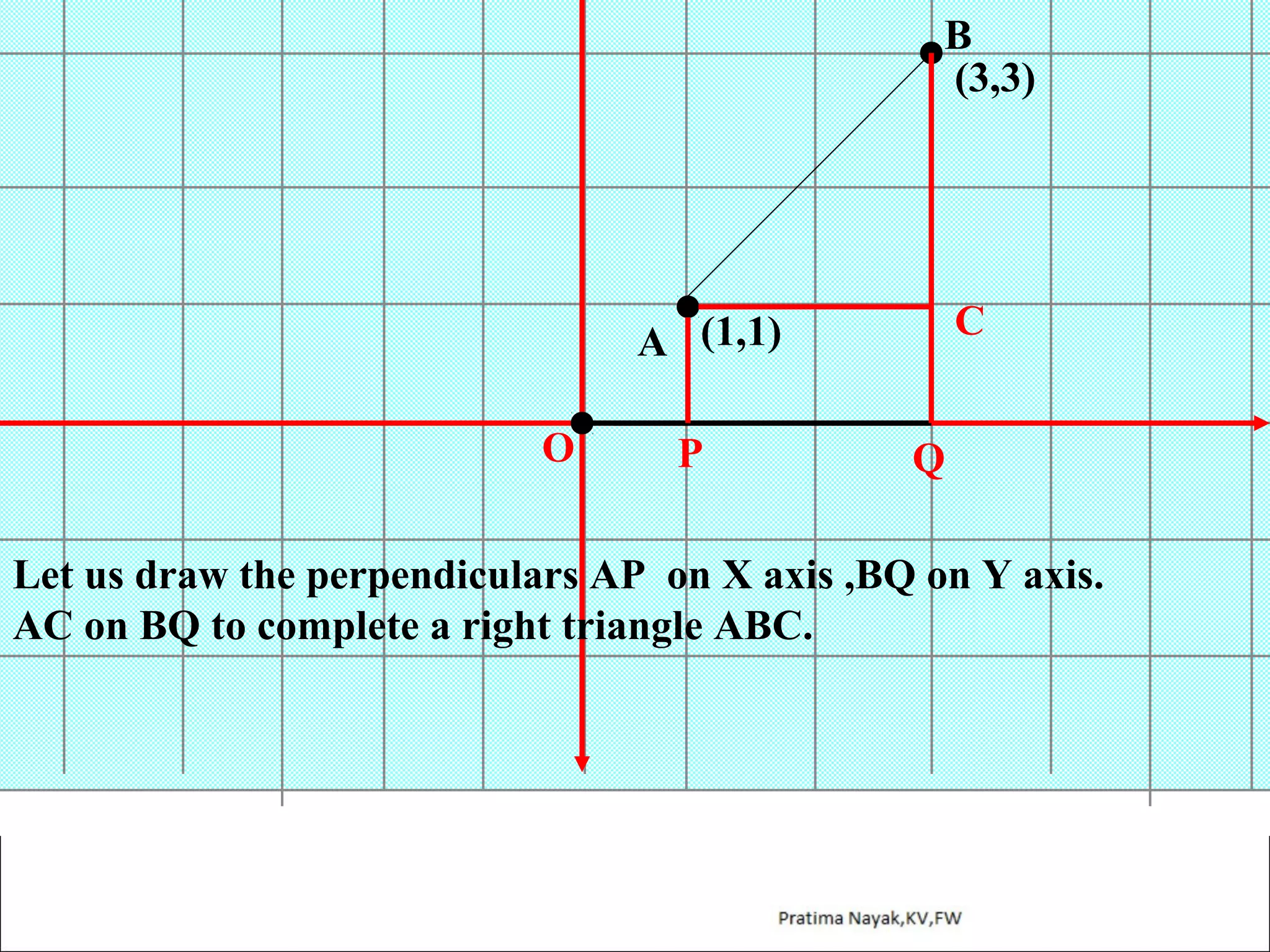
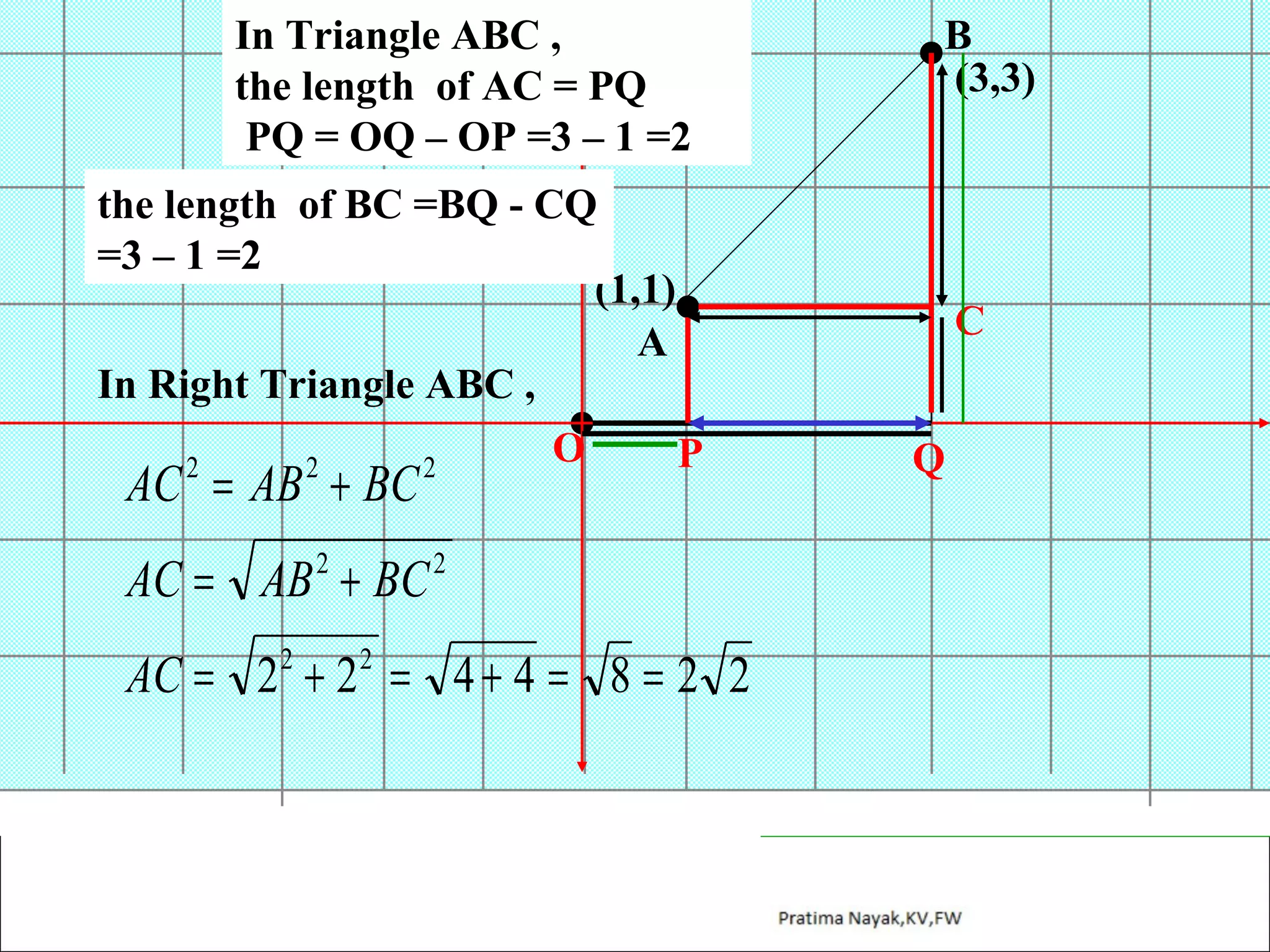
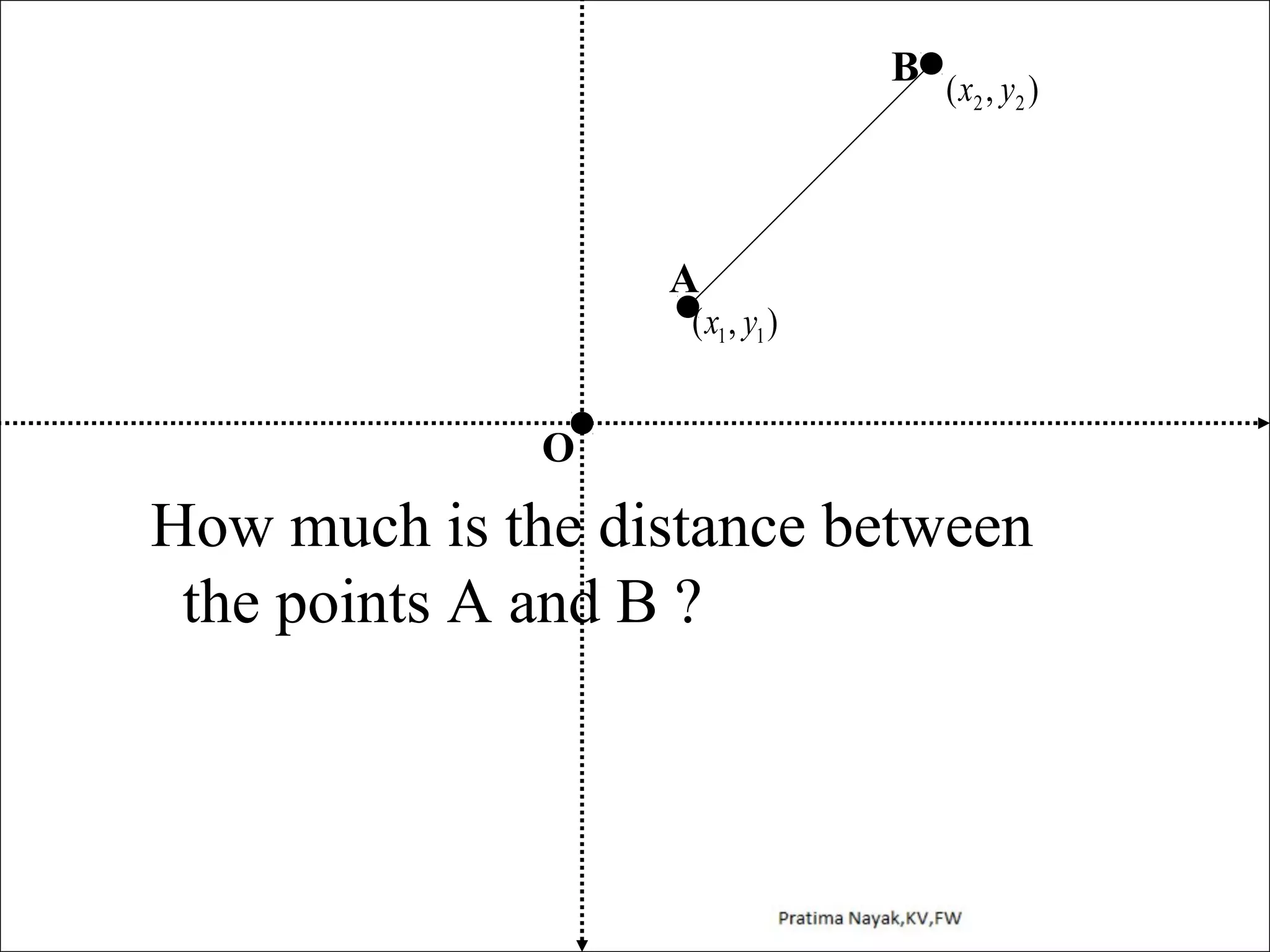
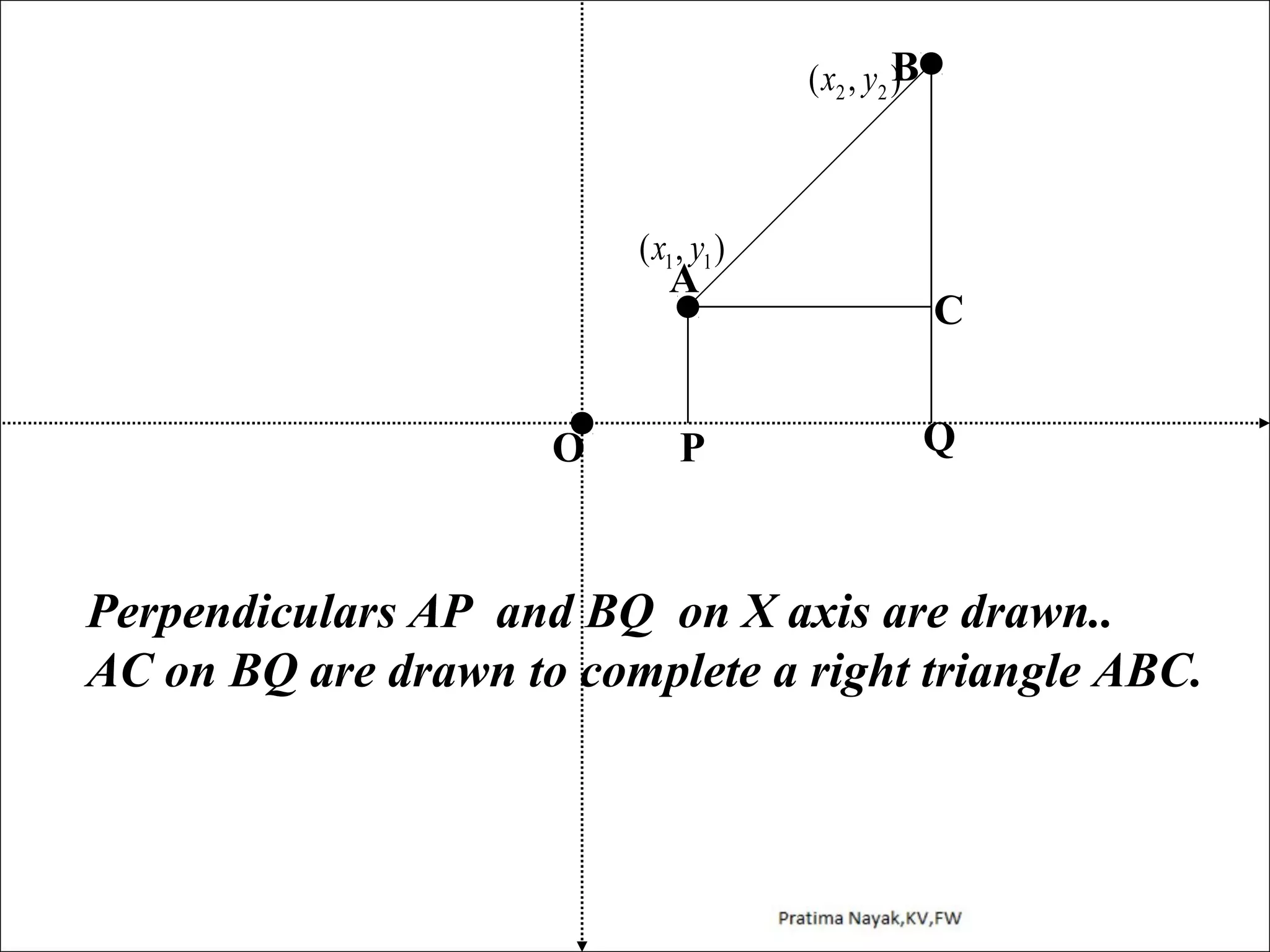
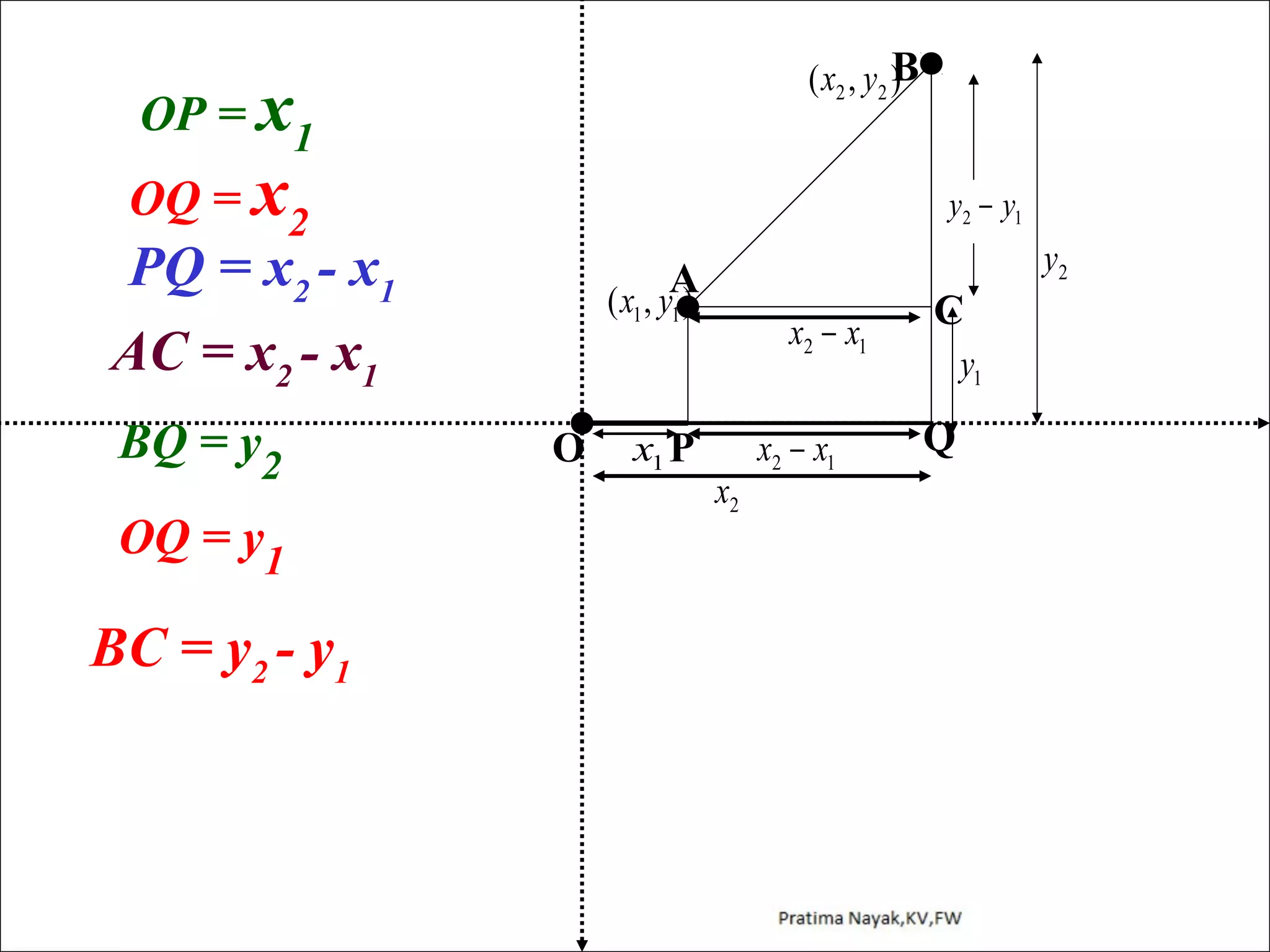
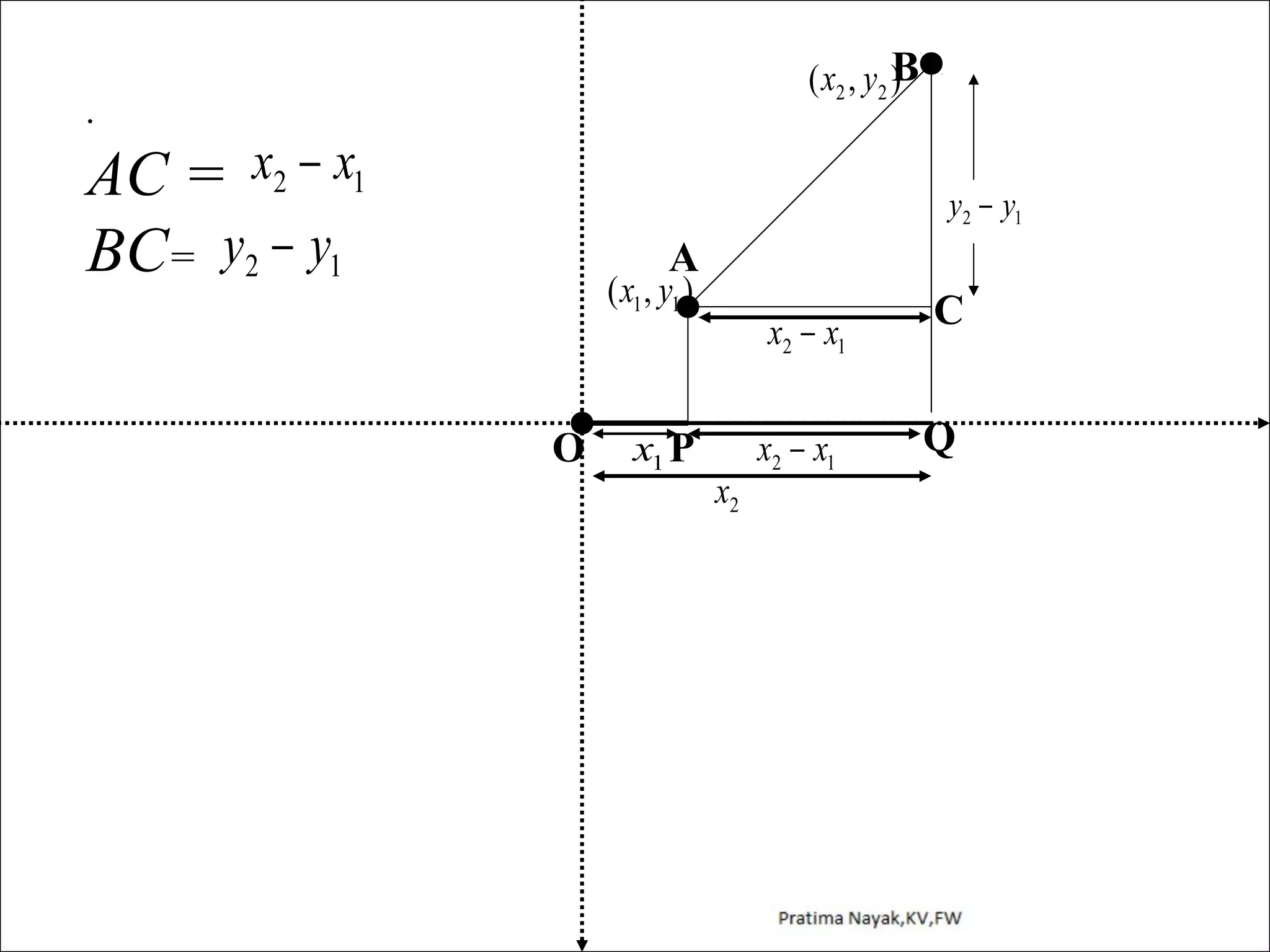
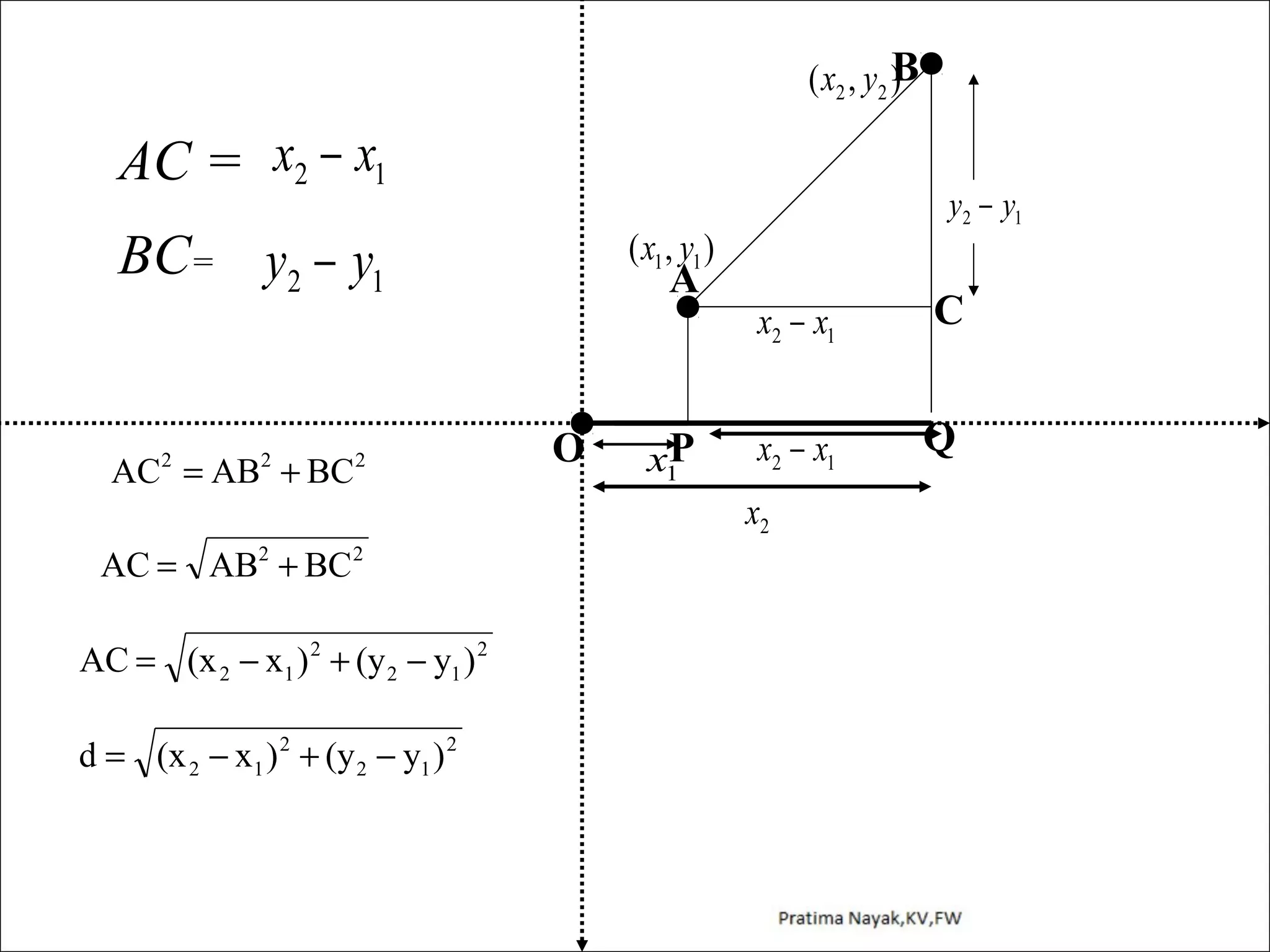
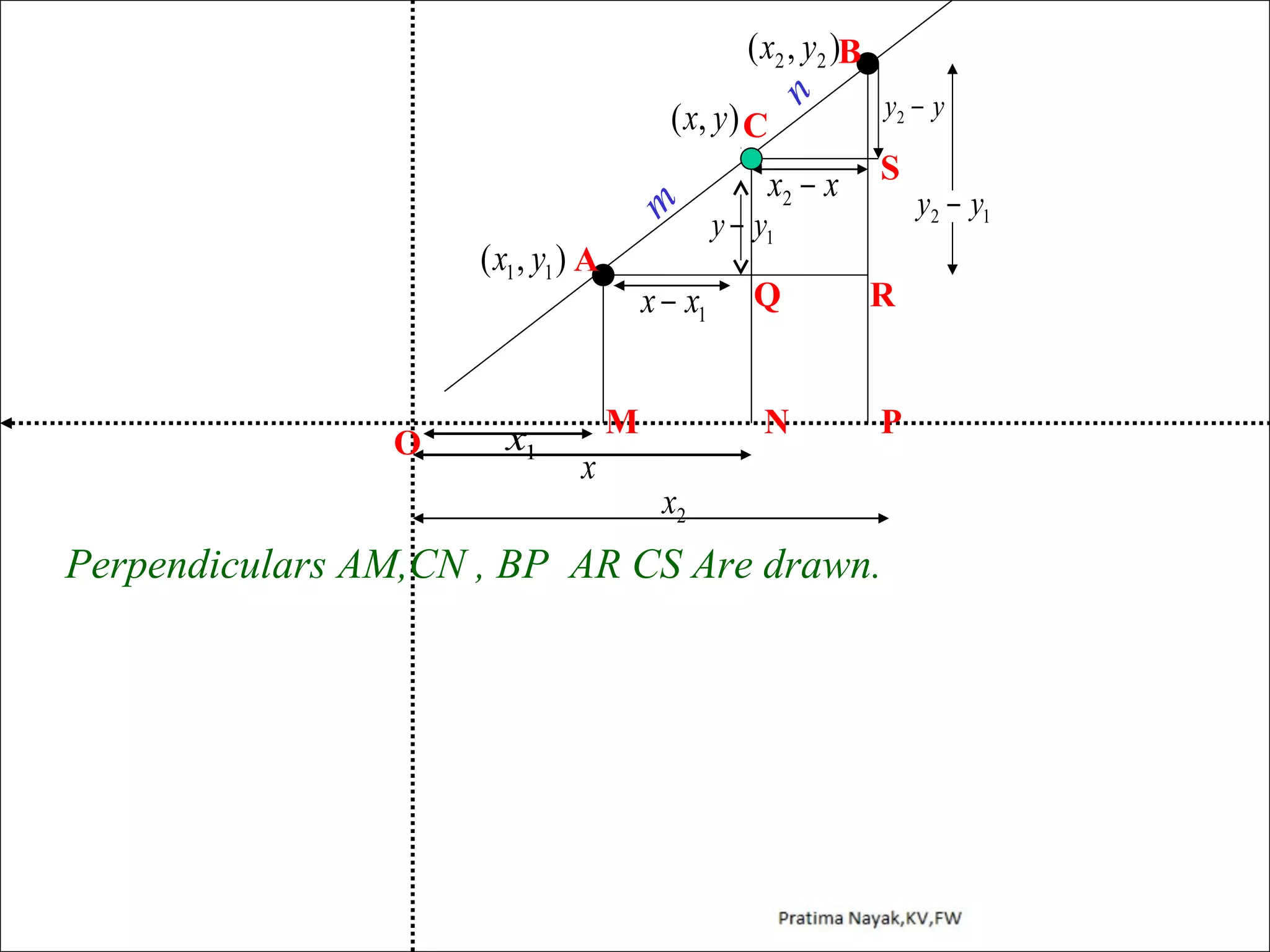
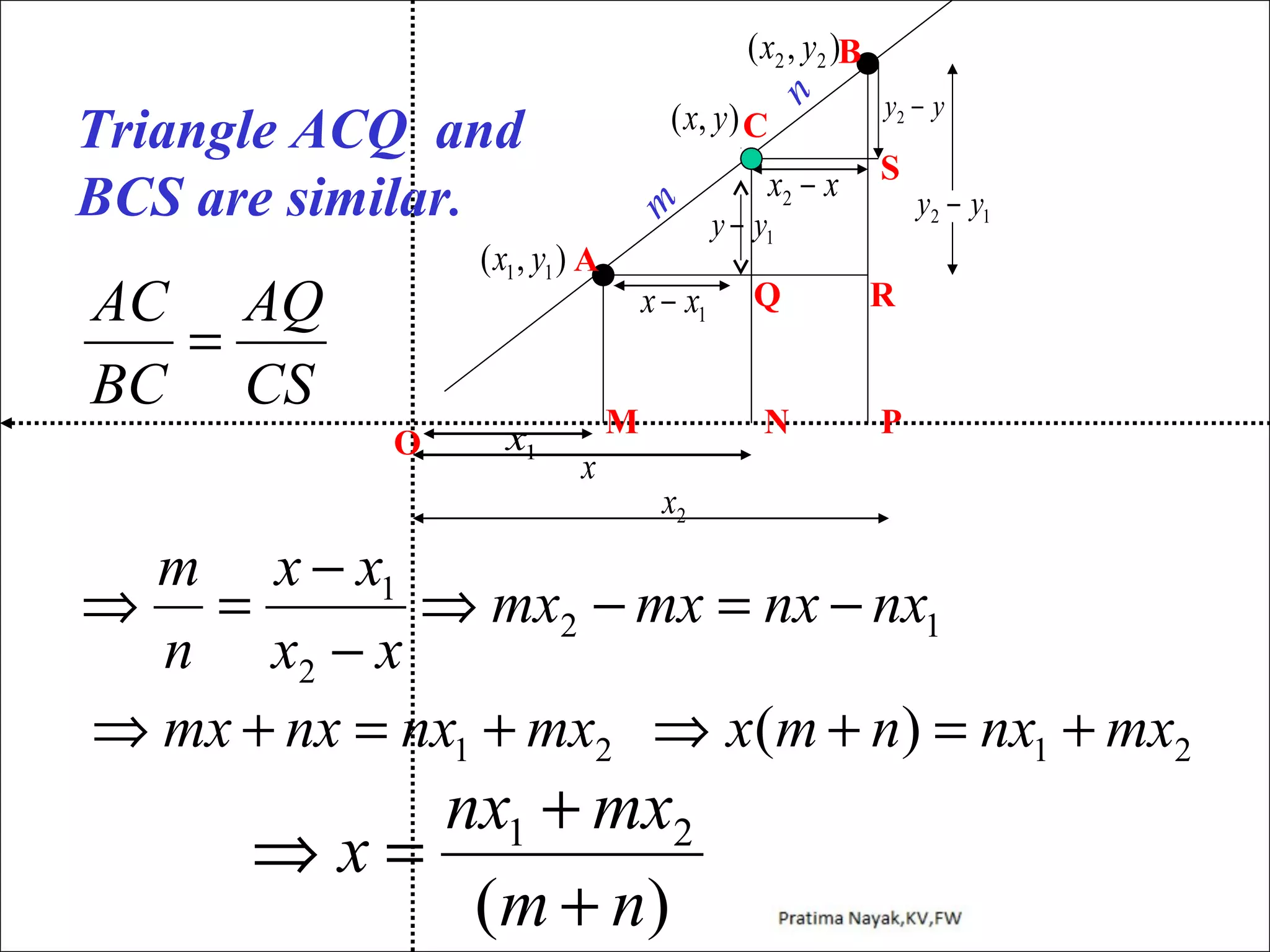
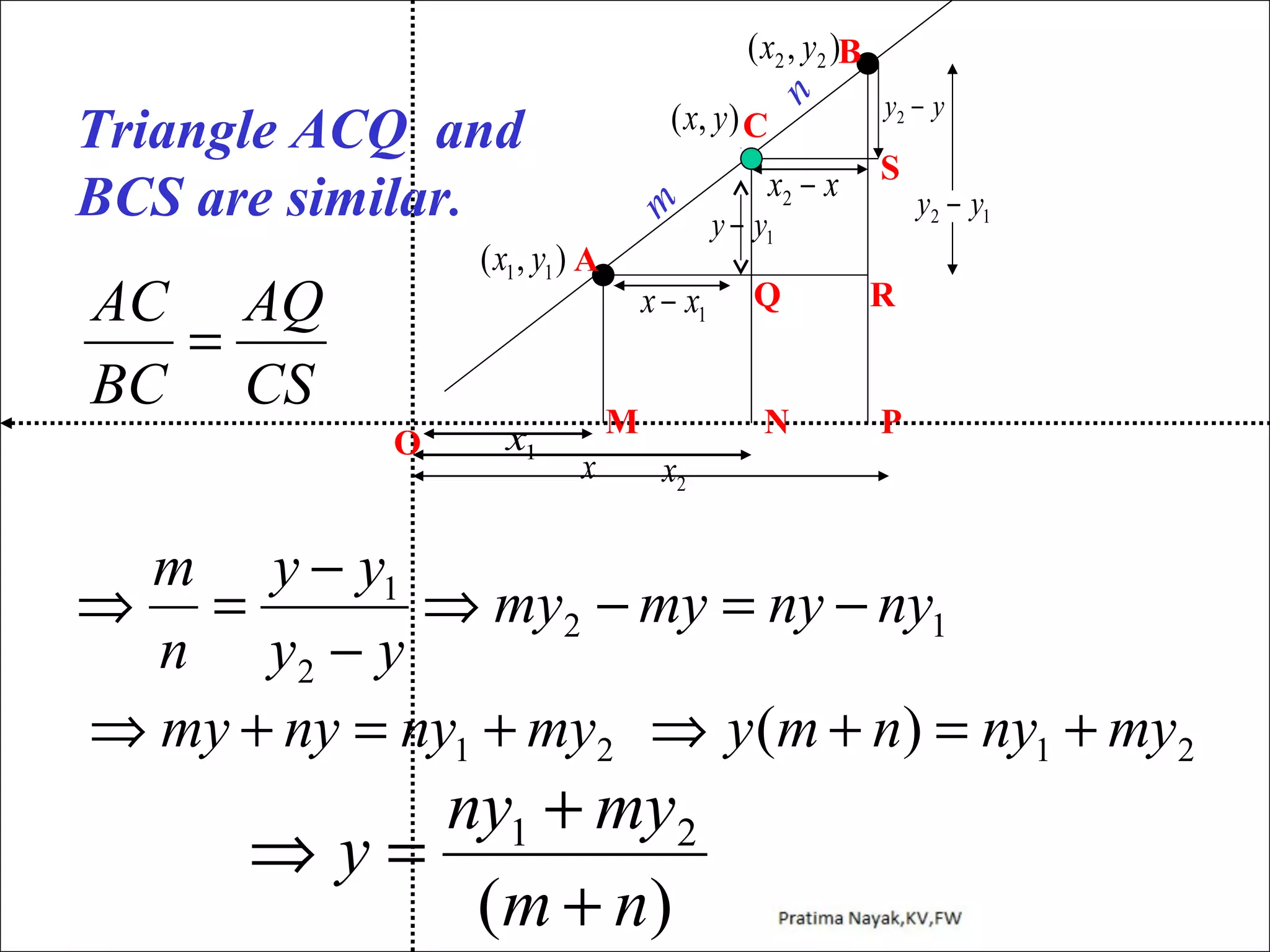
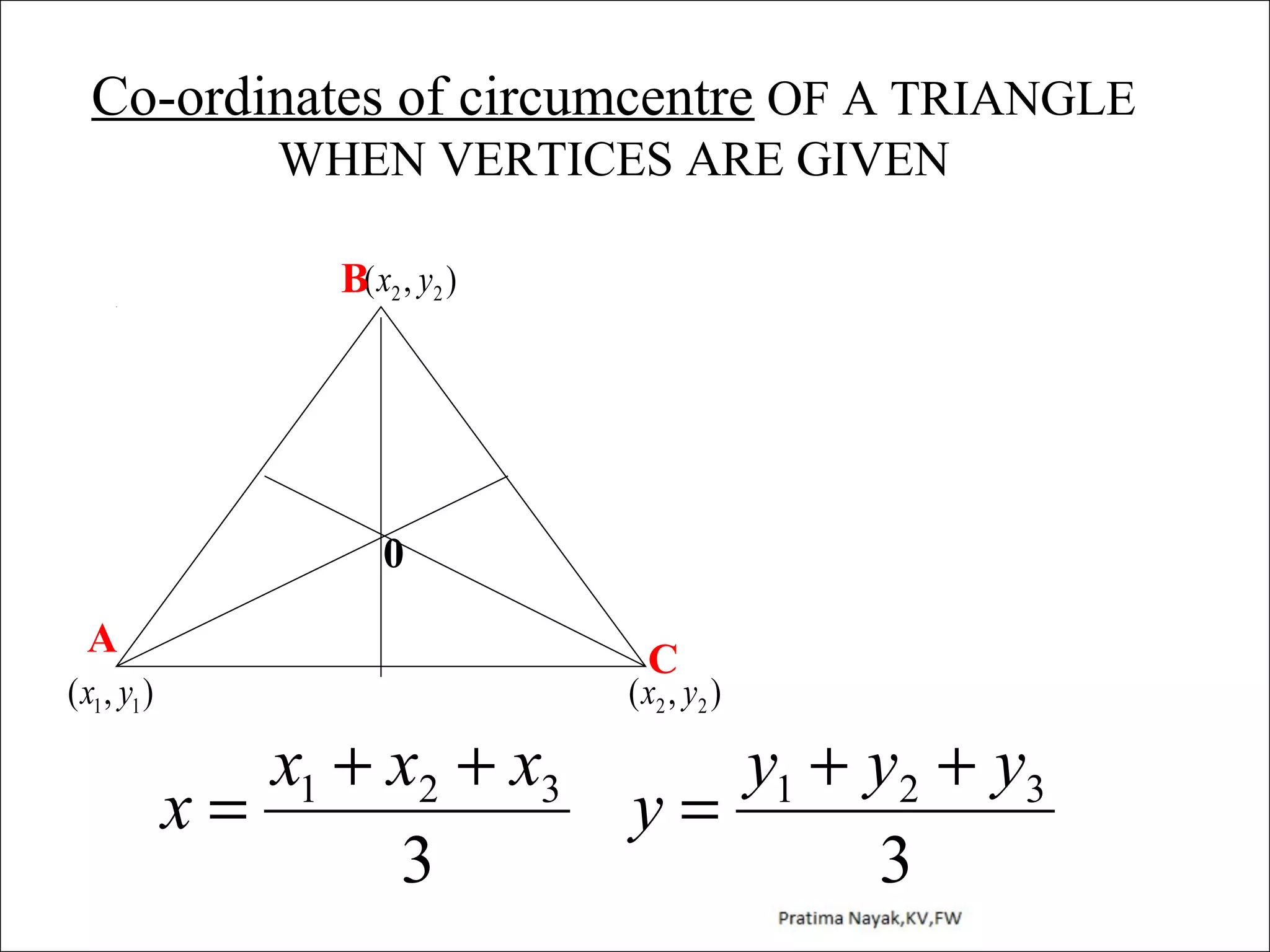
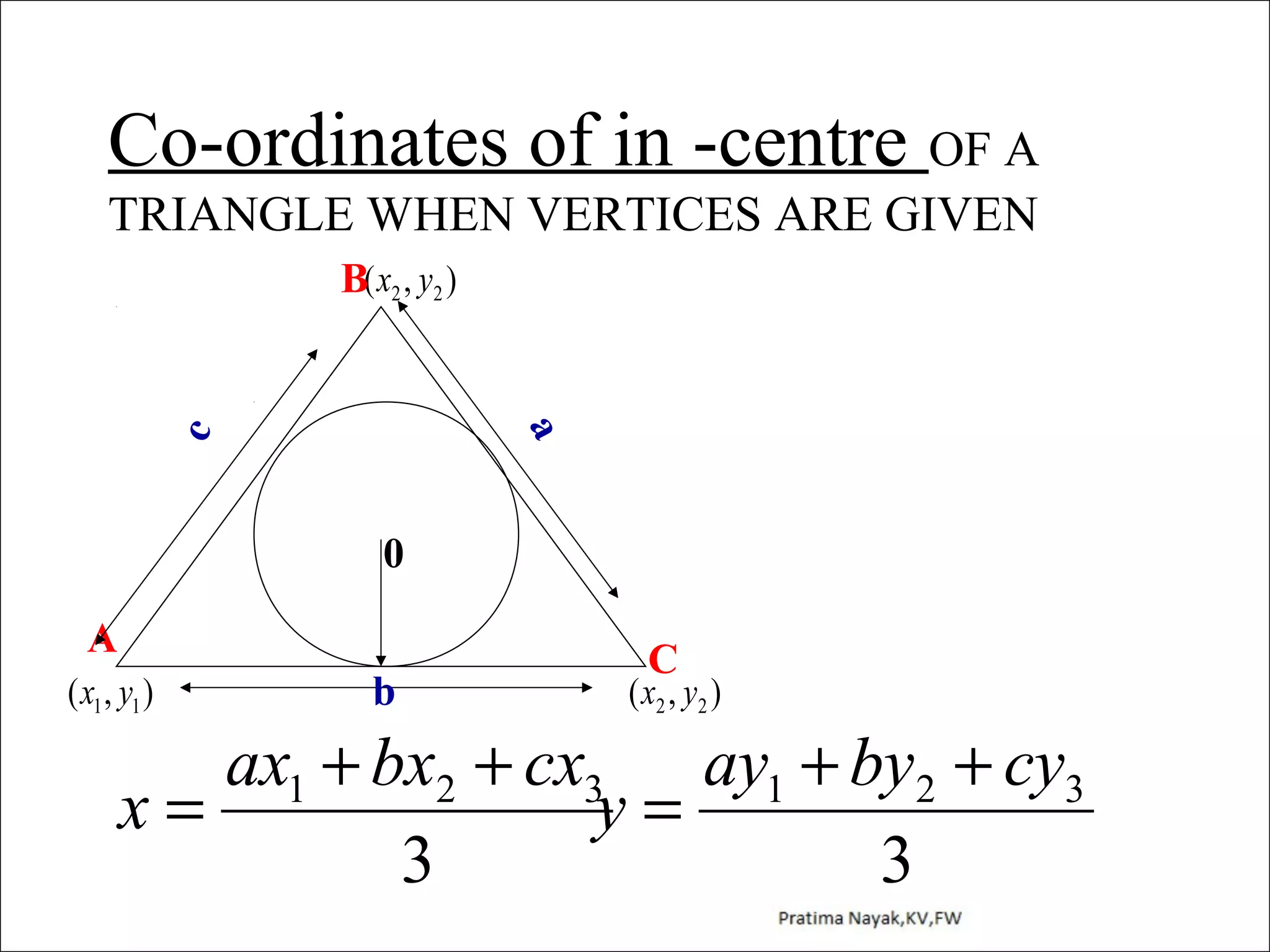
The document discusses distance formula and section formula to find the coordinates of points on a plane. It explains how to find the distance between two given points using the distance formula. It also describes how to find the coordinates of a point C that divides the line segment between points A and B in a given ratio using the section formula. The document provides examples of finding coordinates of circumcenter and incenter of a triangle given its vertices. It concludes with some assignment questions related to these concepts.
More Related Content
Similar to Introduction to coordinate geometry by pratima nayak
More from Pratima Nayak ,Kendriya Vidyalaya Sangathan
Introduction to coordinate geometry by pratima nayak
- 1. How much isthe distance between flower and the butterfly ?
- 3.
- 4.
- 5.
- 6.
- 7. 3 1st quadrant -3 -2 -1 0 1 2 3 4 5 6 -3 3rd quadrant -2 -1 -4 -4 -5 0 1 2 2ndquadrant 4th quadrant
- 8. 3 1 2 To mark apoint on a plane (3, 0) -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 (3, 0) 1 2 3 4 5 6
- 9. 3 2 1 To mark apoint on a plane (-5, 0) 0 0 -1 -1 -2 -2 -3 -3 -4 (-5, 0) -5 -4 1 2 3 4 5 6
- 10. 3 -4 -3 -2 -1 0 1 -1 -5 0 1 2 ( 0,3) -4 -3 -2 To marka point on a plane ( 0,3) 2 3 4 5 6
- 11. 3 -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 1 2 To mark apoint on a plane ( 0,-1) 1 ( 0,-1) 2 3 4 5 6
- 12. 3 2 1 A What are theco-ordinates of A ? 0 0 -1 -1 -2 -2 -3 -3 -4 -4 -5 1 2 3 4 5 6
- 13. 3 To mark apoint on a plane (4, 2 ) -4 -3 -2 -1 0 -1 -5 0 1 2 (4, 2) 1 2 3 -4 -3 -2 4 is x coordinate or abscissa 2 is y coordinate or ordinate. 4 5 6
- 14. 2 3 (3,3) -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 1 To mark apoint on a plane (3,3 ) 1 2 3 4 5 6
- 15.
- 16. 3 1 2 (-3,3) 0 To mark apoint on a plane (-3,3 ) -1 0 -1 -2 -2 -3 -3 -4 -4 -5 1 2 3 4 5 6
- 17.
- 18. -2 -1 0 -1 -3 -2 (-4,-2) -3 -4 -4 -5 0 1 2 3 To mark apoint on a plane (-4,-2) 1 2 3 4 5 6
- 19.
- 20. -1 0 1 2 3 4 -1 -2 -2 -3 -3 -4 -4 -5 0 1 2 3 To mark apoint on a plane (3,-2) (3,-2) 5 6
- 21.
- 22. 3 (-3,-1) -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 1 2 What is thecoordinates of shown point? 1 2 3 4 5 6
- 23. 3 -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 1 2 What is thecoordinates of shown point? 1 2 3 4 5 6
- 24. 3 -1 0 -1 -2 -2 -3 -3 -4 -4 -5 0 1 2 What is thecoordinates of shown point? 1 2 3 4 5 6
- 25. 2 3 A 1 -3 -2 -1 0 -4 0 1 2 3 4 5 6 -3 -2 -1 What are thecoordinates of vertices of the tria -4 -5 C B
- 26. 3 2 1 -2 -1 0 -3 0 1 2 3 4 5 6 -1 -4 -3 -2 What are thecoordinates of vertices of the star -4 -5
- 27. 3 (3,3) 2 To mark apoint on a plane (3,3 ) -1 0 (0,0)1 -1 -2 -2 -3 -3 -4 -4 -5 0 1 Let there is a flower at this point. 2 3 4 5 6
- 28. (3,3) Let there isa butterfly at (1,1) (1,1) (0,0)
- 29. How much isthe distance between flower and the butterfly ? (1,1) (3,3)
- 30. B (3,3) A (1,1) O Let Ais the position of the Butterfly.A has co-ordinates (1,1). B is the position of the flower.B has the coordinate ( 3, 3).
- 31. B (3,3) C A (1,1) O P Q Let usdraw the perpendiculars AP on X axis ,BQ on Y axis. AC on BQ to complete a right triangle ABC.
- 32. In Triangle ABC, the length of AC = PQ PQ = OQ – OP =3 – 1 =2 the length of BC =BQ - CQ =3 – 1 =2 (1,1) A In Right Triangle ABC , O P 2 2 2 AC = AB + BC AC = AB 2 + BC 2 AC = 2 + 2 = 4 + 4 = 8 = 2 2 2 2 B (3,3) C Q
- 33. B (x ,y ) 2 2 A ( x1 , y1 ) O How much is the distance between the points A and B ?
- 34. B ( x2 ,y 2 ) ( x1 , y1 ) A O P C Q Perpendiculars AP and BQ on X axis are drawn.. AC on BQ are drawn to complete a right triangle ABC.
- 35. B ( x2 ,y 2 ) OP = x1 OQ = x2 y2 − y1 PQ = x2 - x1 AC = x2 - x1 BQ = y2 OQ = y1 BC = y2 - y1 y2 A (x , y ) 1 O 1 x1 P x2 − x1 x2 x2 − x1 C y1 Q
- 36. B ( x2 ,y 2 ) . AC = x2 − x1 BC= y2 − y1 y2 − y1 A ( x1 , y1 ) O x1 P x2 − x1 x2 x2 − x1 C Q
- 37. B ( x2 ,y 2 ) AC = x2 − x1 BC= y2 − y1 AC = AB + BC 2 2 2 AC = AB2 + BC 2 AC = (x 2 − x1 ) 2 + (y 2 − y1 ) 2 d = (x 2 − x1 ) 2 + (y 2 − y1 ) 2 y2 − y1 ( x1 , y1 ) A O P x1 x2 − x1 C x2 − x1 Q x2
- 38. B (x ,y ) 2 2 It is called distance formula. A ( x1 , y1 ) O The distance between the points A ( x1 , y1 ) and B ( x2 , y2 ) d = ( x2 − x1 ) + ( y2 − y1 ) 2 2
- 39. B (x ,y ) 2 2 C is a point on the line joining A and B in ratio m:n A ( x1 , y1 ) O
- 40. m:n C ( x,y ) m A and B in ratio n C is a point on the line joining B (x , y ) 2 2 A ( x1 , y1 ) What will be co-ordinates of C?
- 41. n ( x2 ,y2 )B y2 − y x2 − x S m ( x, y ) C ( x1 , y1 ) A O x1 x − x1 Q R N M x y − y1 P x2 Perpendiculars AM,CN , BP AR CS Are drawn. y2 − y1
- 42. n ( x2 ,y2 )B m Triangle ACQ and BCS are similar. ( x1 , y1 ) A AC AQ = BC CS O x1 y2 − y x2 − x S ( x, y ) C x − x1 x2 Q y2 − y1 R N M x y − y1 P m x − x1 ⇒ = ⇒ mx2 − mx = nx − nx1 n x2 − x ⇒ mx + nx = nx1 + mx2 ⇒ x(m + n) = nx1 + mx2 nx1 + mx2 ⇒x= ( m + n)
- 43. n ( x2 ,y2 )B m Triangle ACQ and BCS are similar. ( x1 , y1 ) A AC AQ = BC CS O x1 y2 − y x2 − x S ( x, y ) C x − x1 Q y2 − y1 R N M x y − y1 P x2 m y − y1 ⇒ = ⇒ my2 − my = ny − ny1 n y2 − y ⇒ my + ny = ny1 + my2 ⇒ y (m + n) = ny1 + my2 ny1 + my2 ⇒y= ( m + n)
- 44. This is calledsection formula B C ( x, y ) m:n A m A and B in ratio n C is a point on the line joining ( x2 , y 2 ) ( x1 , y1 ) The co-ordinates of C are : nx1 + mx2 x= ( m + n) ny1 + my2 y= ( m + n)
- 45. in ratio n C isan exterior point point on the line joining A and B B (x , y ) 2 2 m:n A C ( x, y ) m ( x1 , y1 ) The co-ordinates of C are : nx1 − mx2 x= ( m − n) ny1 − my2 y= ( m − n)
- 46. Co-ordinates of circumcentreOF A TRIANGLE WHEN VERTICES ARE GIVEN B( x2 , y2 ) 0 A ( x1 , y1 ) C x1 + x2 + x3 x= 3 ( x2 , y 2 ) y1 + y2 + y3 y= 3
- 47. Co-ordinates of in-centre OF A TRIANGLE WHEN VERTICES ARE GIVEN B( x2 , y2 ) c a 0 A ( x1 , y1 ) b C ( x2 , y 2 ) ax1 + bx2 + cx3 ay1 + by2 + cy3 x= y= 3 3
- 48. ASSIGNMENT Q1.Which point onx axis is equidistant from (5,9) and (-4,6)? Q2. Which point on y axis is equidistant from (2,3) and (-4,1)?
- 49. ASSIGNMENT Q3.Prove that (2a,4a),(2a,6a)and(2a+√3a) are vertices of an equilateral triangle. Q4.In what ratio the x-axis divide the line segment joining the points (2,-3) and (5,6)?
- 50. ASSIGNMENT Q5. For whatvalue of x will the points (x,1),(2,1) and (4,5) lie on a line? Q6. Determine the ratio in which the line 3x+y-9=0 divides the segment joining the points (1,3) and (2,7)?
- 51. ASSIGNMENT Q7If the points(-2,-1), (1,0),(x,3) and ( 1,y) form a parallelogram, find the value of x and y. Q8.Find the coordinates of (i) centroid ii)incentre (iii)circumcentre of of the triangle whose vertices are (0,6),(8,12) and ( 8,0)
- 52. Thank You Developed byPratima Nayak, Kendriya Vidyalaya,Fort Willia,Kolkata