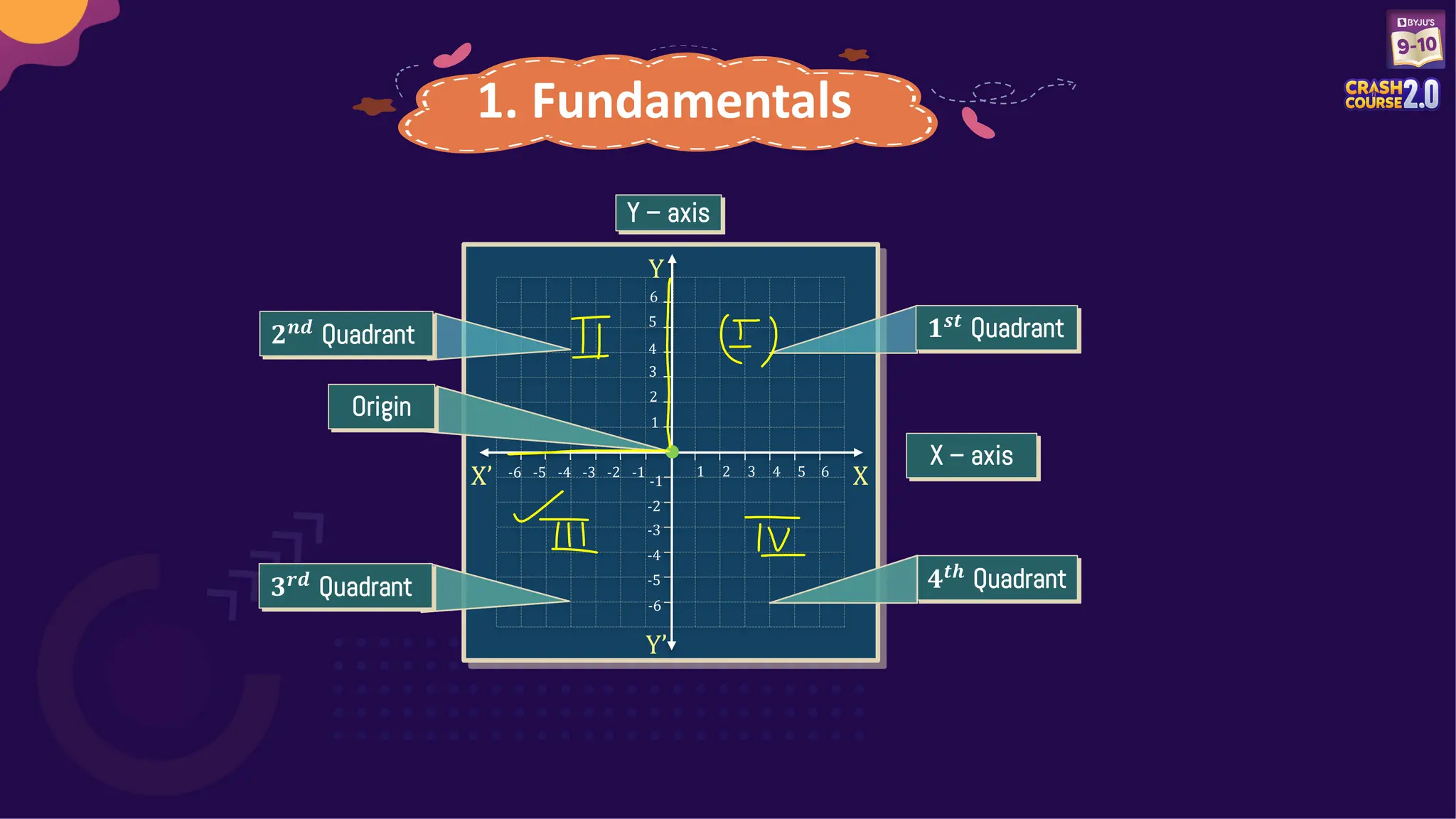
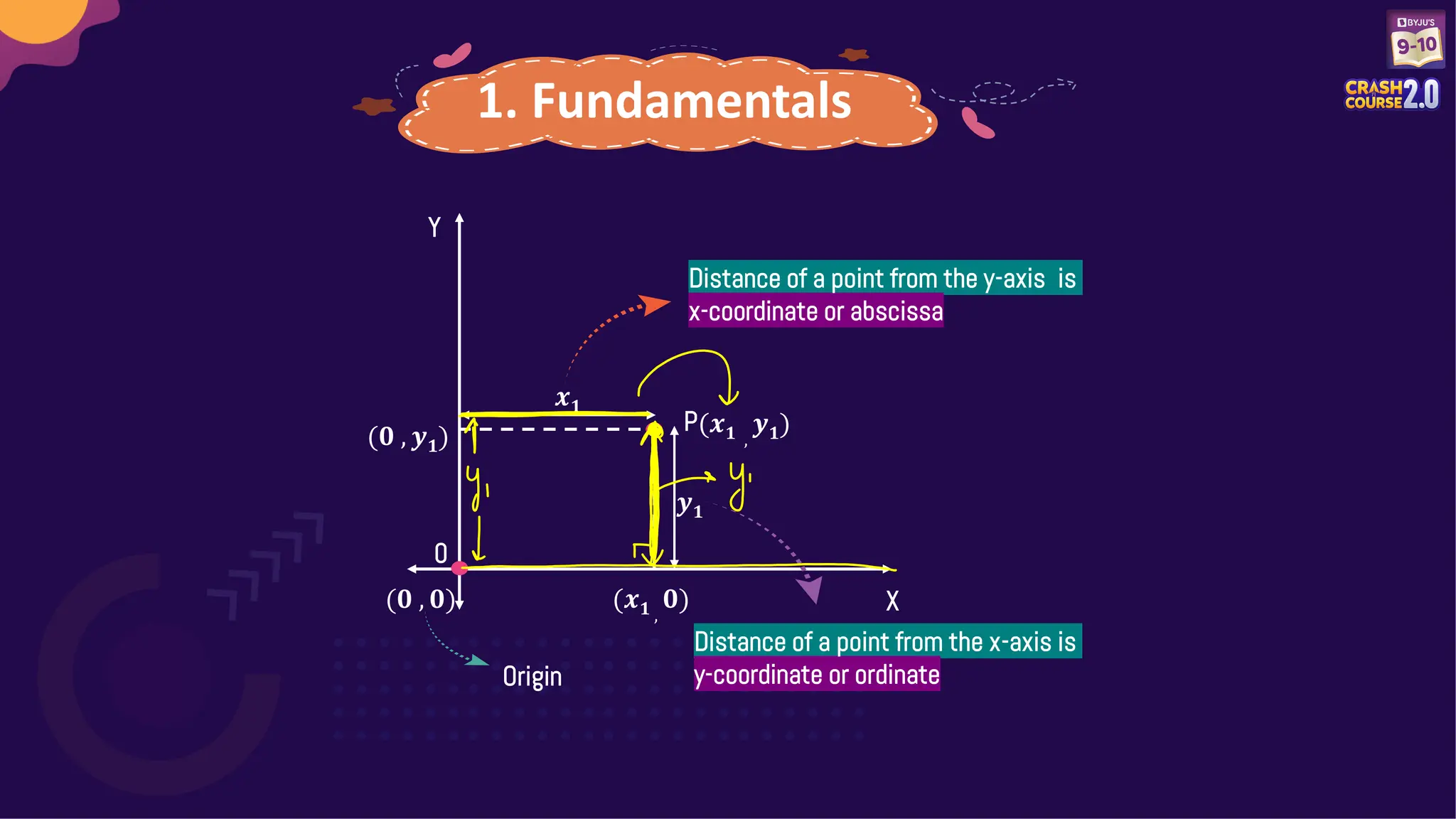
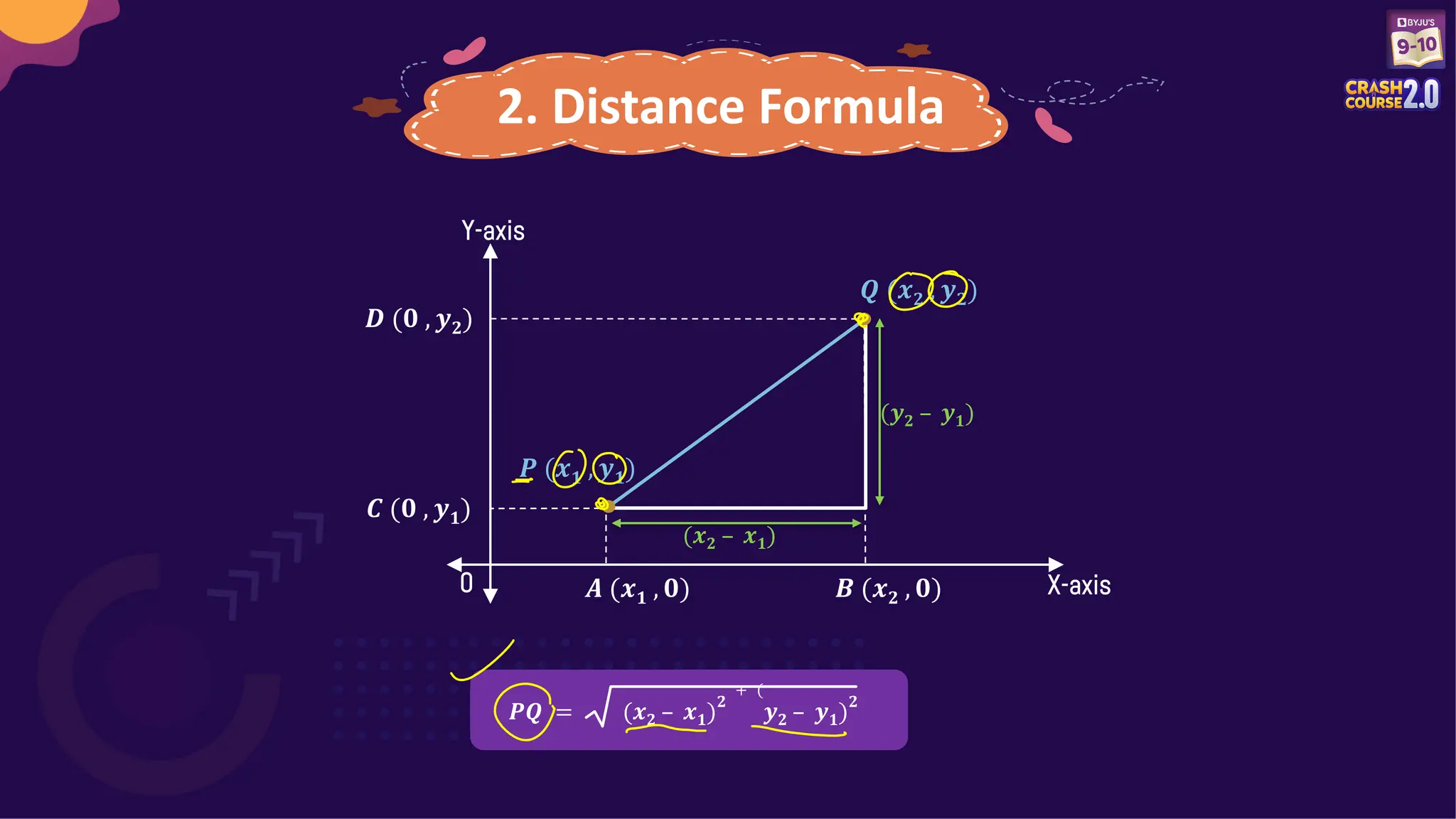
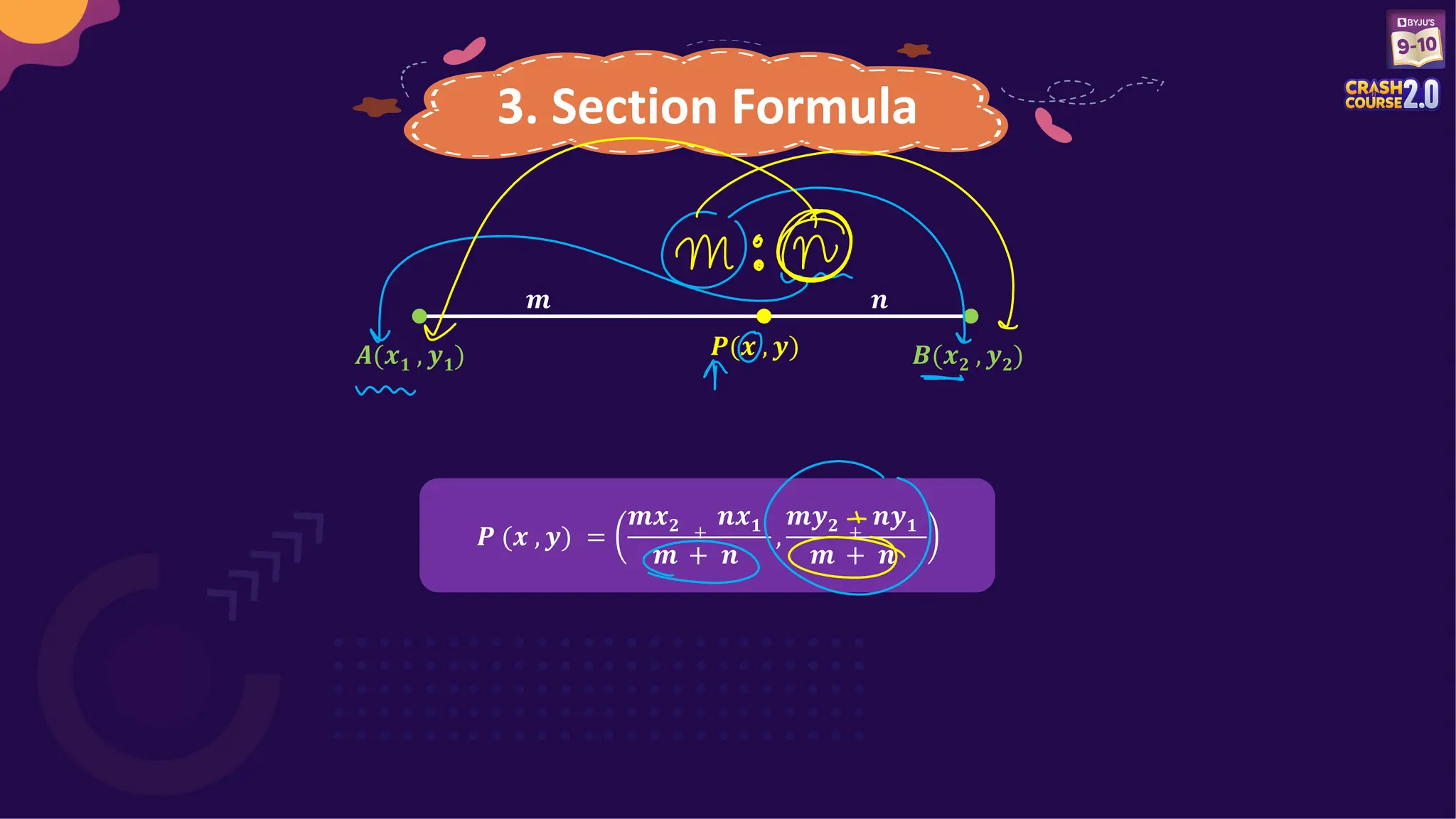
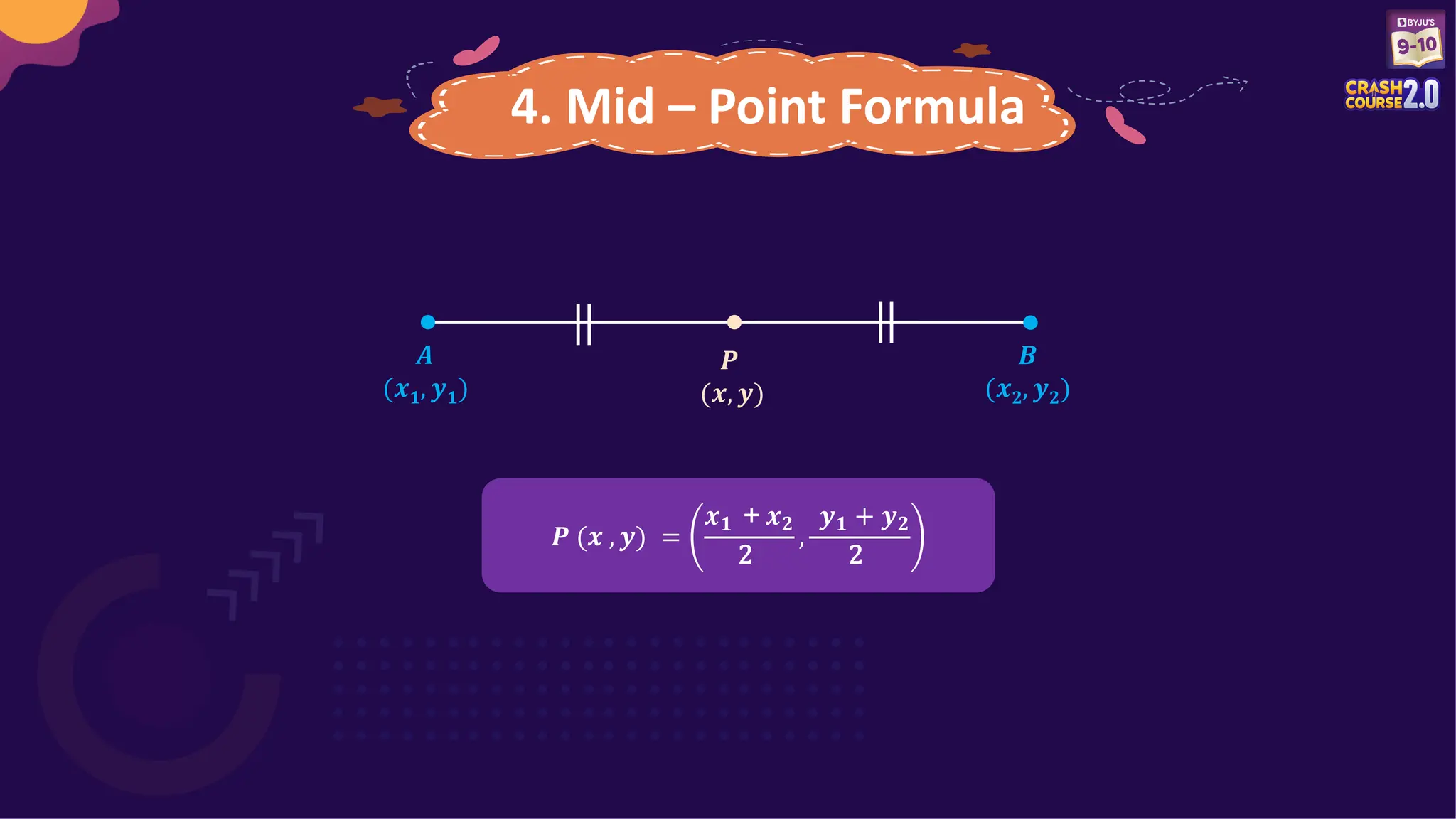
Unit 3 covers the fundamentals of coordinate geometry, including the distance formula, section formula, and midpoint formula. Several questions on finding distances, coordinates, and area of geometric figures are presented for practice. Additionally, details about an upcoming exam and the opportunity for scholarships are included.

1. Unit 3 : Coordinate Geometry
Chapter 7 : Coordinate Geometry

6. 1. Fundamentals
2. Distance Formula
3. Section Formula
4. Mid – Point Formula
Topics

7. 1. Fundamentals
1
2
3
4
5
6
1 2 3 4 5 6
-1
-2
-3
-4
-5
-6
Y
X
X’
Y’
-1
-2
-3
-4
-5
-6
𝟏𝒔𝒕 Quadrant
X – axis
Y – axis
𝟐𝒏𝒅
Quadrant
𝟒𝒕𝒉
Quadrant
𝟑𝒓𝒅
Quadrant
Origin

8. 1. Fundamentals
X
0
Y
(𝒙𝟏 ,
𝒚𝟏)
P
𝒚𝟏
𝒙𝟏
(𝒙𝟏 ,
𝟎)
(𝟎 , 𝒚𝟏)
(𝟎 , 𝟎)
Origin
Distance of a point from the x-axis is
y-coordinate or ordinate
Distance of a point from the y-axis is
x-coordinate or abscissa

9. 2. Distance Formula
𝑷 (𝒙𝟏 , 𝒚𝟏)
𝑸 (𝒙𝟐 , 𝒚𝟐)
0
𝑫 (𝟎 , 𝒚𝟐)
𝑪 (𝟎 , 𝒚𝟏)
𝑨 (𝒙𝟏 , 𝟎) 𝑩 (𝒙𝟐 , 𝟎)
Y-axis
X-axis
(𝒙𝟐 – 𝒙𝟏)
(𝒚𝟐 – 𝒚𝟏)
𝑷𝑸 = (𝒙𝟐 – 𝒙𝟏)
𝟐
+ (
𝒚𝟐 – 𝒚𝟏)
𝟐

10. 3. Section Formula
𝒎 𝒏
𝑷(𝒙 , 𝒚) 𝑩(𝒙𝟐 , 𝒚𝟐)
𝑨(𝒙𝟏 , 𝒚𝟏)
𝑷 (𝒙 , 𝒚) =
𝒎𝒙𝟐 +
𝒏𝒙𝟏
𝒎 + 𝒏
,
𝒎𝒚𝟐 +
𝒏𝒚𝟏
𝒎 + 𝒏
𝑷 (𝒙 , 𝒚) =
𝒎𝒙𝟐 +
𝒏𝒙𝟏
𝒎 + 𝒏
,
𝒎𝒚𝟐 +
𝒏𝒚𝟏
𝒎 + 𝒏

11. 4. Mid – Point Formula
𝑨
(𝒙𝟏, 𝒚𝟏)
𝑷
(𝒙, 𝒚)
𝑩
(𝒙𝟐, 𝒚𝟐)
𝑷 (𝒙 , 𝒚) =
𝒙𝟏 + 𝒙𝟐
2
,
𝒚𝟏 + 𝒚𝟐
2

13. Question 1

14. Find the ratio in which y-axis divides the line segment joining the
points A(5, –6) and B(–1, –4). Also find the coordinates of the
point of division.
Question 2

15. Find the value of k, if the point A(0, 3) is equidistant from P(3, k)
and Q(k, 4).
Question 3

16. Find the perimeter of the triangle formed by the points (0, 0),
(2, 0) and (0, 2).
Question 4

17. Find the point on the x-axis which is equidistant from (2, –5) and
(–2, 9).
Question 5

18. Find the points of trisection of the line segment joining the points
A(-4, 3) and B(2, -1).
Question 6

19. If the point C(–1, 2) divides internally the line segment joining
A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B.
Question 7

20. In what ratio is the line segment joining the points (-1, 3) and
(4, -7) divided by the point (2, -3)?
Question 8

21. Let P and Q be the points of trisection of the line segment joining
the points A(2, – 2) and B(–7, 4) such that P is nearer to A. Find
the coordinates of P and Q.
Question 9

22. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.
Question 10

23. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4)
and (– 2, – 1) taken in order.
[Hint : Area of a rhombus =
𝟏
𝟐
× (product of its diagonals)]
Question 11

24. Find the coordinates of point A, where AB is the diameter of a
circle whose center is (2, – 3) and point B is (1, 4).
Question 12

25. The points (𝒂, 𝒂), (−𝒂, −𝒂) and (− 𝟑𝒂, 𝟑𝒂) are the vertices of
a/an ……… triangle.
Question 13

26. The x-coordinate of a point P is twice its y-coordinate. If P
is equidistant from Q(2, -5) and R(-3, 6), find the coordinates
of P.
Question 14

27. If two vertices of an equilateral triangle be (𝟎, 𝟎), 𝟑, 𝟑 , find
the third vertex.
Question 15

28. Take the test for
FREE
Registration link in description!
Exam Dates:
21st Jan - 22nd Jan
28th Jan - 29th Jan
4th Feb - 5th Feb

29. Stand A Chance
to Win Big
Get Scholarships* worth
100 Crore
And exciting Cash Awards*
*T&C Apply
Get A 15-Page Personalised
Academic Report
● Overall Analysis
● Skillset Analysis
● Behavioural Analysis
● Subject Analysis
● Capability Analysis
● Career Inclinations

30. Go to: www.menti.com
Code: 7126 9895