Download as PDF, PPTX
Uploaded byQingkai Kong
Introduction to Artificial Neural Network
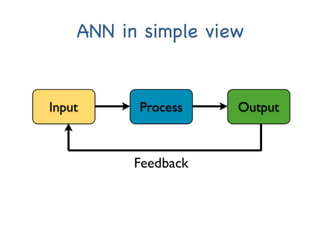
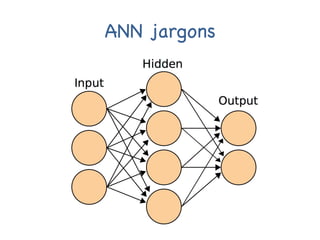
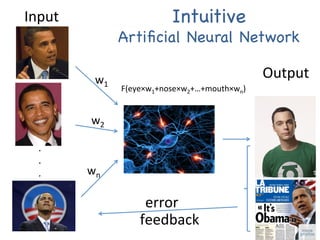
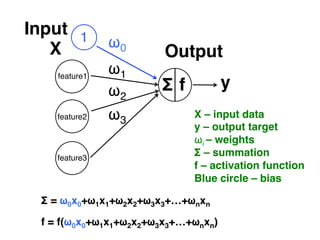
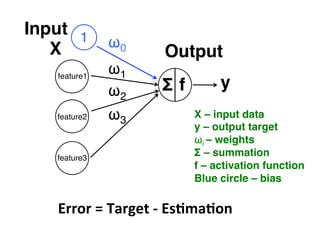
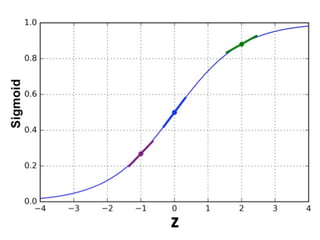
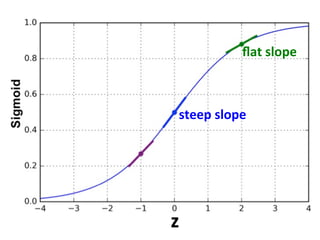
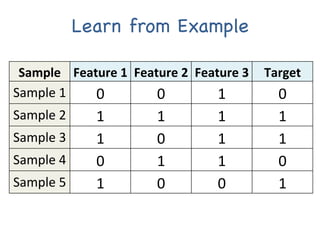
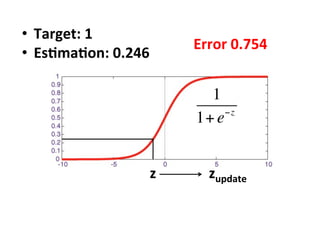
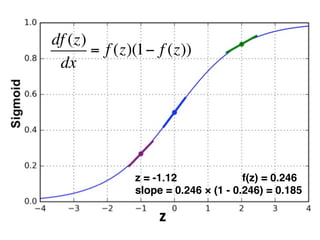
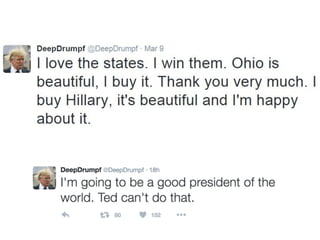
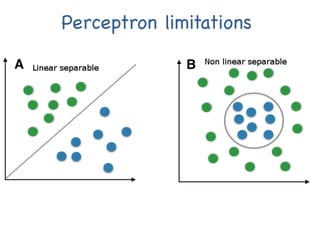
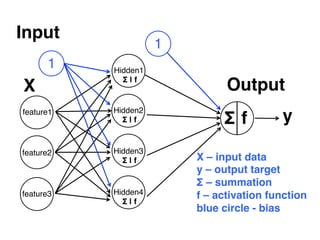
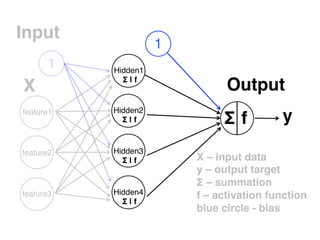
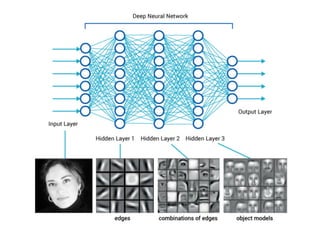
The document provides an introductory overview of artificial neural networks (ANNs) and machine learning, discussing their history, key concepts, and applications. It explains ANN structure, learning process, error reduction, and different cases related to error handling in predictions. Additionally, it references various resources and examples for further learning about ANN and machine learning practices.
More Related Content
Similar to Introduction to Artificial Neural Network
![[DSC Europe 25] Bojan Djuricic - Predictive Design Process.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/5awdrbedqdek3gqu2ezy-4-the-predictive-design-bojan-djuricic-260120105856-6c399e9b-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Andrzej Kowalczyk - AI - how to start small and grow in the f...](https://cdn.slidesharecdn.com/ss_thumbnails/oy1zmo94qv6vpcqjvno2-andrzej-kowalczyk-ai-how-to-start-small-and-grow-in-the-future-1-260119121559-cf093b23-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Danilo Djukanovic - From Vibes to KPIs: Turning Culture Into ...](https://cdn.slidesharecdn.com/ss_thumbnails/inqestws5wf0cik2glgv-3-danilo-djukanovic-from-vibes-to-kpis-presentation-260114111931-dacff81f-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Stefan Brankovic - #ResumeIsDead. AI-Powered Interviews and C...](https://cdn.slidesharecdn.com/ss_thumbnails/qnmbsv0xq3uysdrq3sev-2-stefan-brankovic-job-bolt-260114111931-a065aa3d-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Mijat Kustudic - Building Financial Intelligence with AI Agen...](https://cdn.slidesharecdn.com/ss_thumbnails/38y2lb5lse6wstegtvas-3-mijat-kustudic-building-financial-intelligence-with-ai-agents-260114111931-1a4783ce-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Ivan Lukovic & Marija Djukic - From Data to Value: Why Maturi...](https://cdn.slidesharecdn.com/ss_thumbnails/ahrfps8xr6knowwhacxh-1-ivan-marija-dsc-2025-ld-v1-presentation-260115093812-be21adfc-thumbnail.jpg?width=640&height=640&fit=bounds)
Introduction to Artificial Neural Network
- 2. Artificial Neural Networkbasics Qingkai Kong 2016-12-02 h"p://seismo.berkeley.edu/qingkaikong/
- 4. Workshop time Learningcurve Gentle introduction Stepby step ANN Real world example h"ps://github.com/qingkaikong/20161202_ANN_basics
- 5. Workshop time Learningcurve Gentle introduction • What’s ML • ANN history • ANN overview Step by step ANN Real world example h"ps://github.com/qingkaikong/20161202_ANN_basics
- 6. What is machinelearning? h"ps://github.com/qingkaikong/20161202_ANN_basics
- 7. Self-driving car Voice recognition … h"ps://github.com/qingkaikong/20161202_ANN_basics
- 8.
- 10.
- 13. ANN in simpleview
- 14.
- 15.
- 17. . . . w1 w2 wn F(eye×w1+nose×w2+…+mouth×wn) Sheldon Cooper? Intuitive Artificial Neural Network Output Input
- 18. . . . w1 w2 wn F(eye×w1+nose×w2+…+mouth×wn) Sheldon Cooper? Intuitive Artificial Neural Network Output Input feedback error
- 19. . . . w1 w2 wn F(eye×w1+nose×w2+…+mouth×wn) Sheldon Cooper? Intuitive Artificial Neural Network Output Input feedback error
- 20. . . . w1 w2 wn F(eye×w1+nose×w2+…+mouth×wn) Intuitive Artificial Neural Network Output Input
- 21. Workshop time Learningcurve Gentle introduction • What’s ML • ANN history • ANN overview Step by step ANN • Perceptron • Backpropagation Real world example
- 23.
- 24.
- 26. X Σ yf Input Output feature2 feature3 ω0 ω2 ω3 X –input data y – output target ωi – weights Σ – summation f – activation function Blue circle – bias feature1 ω1 1 Σ = ω0x0+ω1x1+ω2x2+ω3x3+…+ωnxn f = f(ω0x0+ω1x1+ω2x2+ω3x3+…+ωnxn)
- 28. z = ω0x0+ω1x1+ω2x2+ω3x3+…+ωnxn 1 1+e−z More activation function f (z) = 1 1+e−z df (z) dx = f (z)(1− f (z))
- 29. X Σ yf Input Output feature2 feature3 ω0 ω2 ω3 X –input data y – output target ωi – weights Σ – summation f – activation function Blue circle – bias feature1 ω1 1 Σ = ω0x0+ω1x1+ω2x2+ω3x3+…+ωnxn f = f(ω0x0+ω1x1+ω2x2+ω3x3+…+ωnxn) y This is our estimation Perceptron
- 30. X Σ yf Input Output feature2 feature3 ω0 ω2 ω3 X –input data y – output target ωi – weights Σ – summation f – activation function Blue circle – bias feature1 ω1 1 Error = Target -‐ Es-ma-on Perceptron
- 32. Error = Target -‐ Es-ma-on How the ANN learns
- 33. Error = Target -‐ Es-ma-on How the ANN learns Learning: Update weights to reduce error next -me!
- 35. Weights Delta = Error × slope × input Weights update rules How much we will update the weights for next Xme
- 36. Error = Target -‐ Es-ma-on Look at errors closer 0 1 Target
- 37. Error = Target -‐ Es-ma-on Three cases: • Error 0: Target is 0, es-ma-on is not 0 • Error 0: Target is 1, es-ma-on is not 1 • Error = 0: Es-ma-on correct Look at errors closer 0 1 Target
- 38. Cases 1: • Error 0: Target is 0, es-ma-on is not 0 Look at errors closer (assume inputs are positive)
- 39. Cases 1: • Target is 0 • Es-ma-on is 0.3 Look at errors closer (assume inputs are positive) Error = 0 – 0.3 =-‐0.3
- 40. Cases 1: • Target is 0 • Es-ma-on is 0.3 Look at errors closer (assume inputs are positive) 1 1+e−z z zupdate Error = 0 – 0.3 =-‐0.3
- 41. Cases 1: • Target is 0 • Es-ma-on is 0.3 Look at errors closer (assume inputs are positive) Error = 0 – 0.3 =-‐0.3 z = ω0x0+ω1x1+ω2x2+ω3x3 We need reduce weights!
- 42. Cases 1: • Target is 0 • Es-ma-on is 0.3 Look at errors closer (assume inputs are positive) Error = 0 – 0.3 =-‐0.3 z = ω0x0+ω1x1+ω2x2+ω3x3 We need reduce weights! If we add error to the weights, we will reduce it!
- 43. Cases 1: • Target is 0 • Es-ma-on is 0.3 Look at errors closer (assume inputs are positive) Error = 0 – 0.3 =-‐0.3 z = ω0x0+ω1x1+ω2x2+ω3x3 We need reduce weights! But what if the inputs are negative
- 44. Weights Delta = Error × input Weights update rules
- 45.
- 46. z flat slope steep slope
- 47. Weights Delta = Error × slope × input Weights update rules
- 48.
- 50. Learn from Example Sample Feature 1 Feature 2 Feature 3 Target Sample 1 0 0 1 0 Sample 2 1 1 1 1 Sample 3 1 0 1 1 Sample 4 0 1 1 0 Sample 5 1 0 0 1
- 51. How to dealwith errors X Σ yf Input Output 1 1 -0.166 -1.000 -0.395 1 0.441 1 Σ = (-0.166)×1 + 0.441×1 + (-1)×1 + (-0.395)×1 = -1.12 f(-1.12) = 1/(1+e-1.12) = 0.246 Error = 1 – 0.246 = 0.754 Sample Feature 1 Feature 2 Feature 3 Target Sample 1 1 1 1 1
- 52. 1 1+e−z z zupdate • Target: 1 • Es-ma-on: 0.246 Error 0.754
- 53. 1 1+e−z z zupdate • Target: 1 • Es-ma-on: 0.246 Error 0.754 We want to increase the weights next -me to have larger z
- 54. Weights delta = 0.754 × slope × input
- 55. z df (z) dx =f (z)(1− f (z)) z = -1.12 f(z) = 0.246 slope = 0.246 × (1 - 0.246) = 0.185
- 56. Change item = 0.754 × 0.185 × 1 1 1 1 0.139 0.139 0.139 0.139 =
- 57. -‐0.166 0.441 -‐1.000 -‐0.395 0.139 0.139 0.139 0.139 Updated Weights + = -‐0.027 0.580 -‐0.861 -‐0.256 = Changes of the error Original Weights updates
- 58. -‐0.166 0.441 -‐1.000 -‐0.395 0.139 0.139 0.139 0.139 Updated Weights z = (-0.027)×1 + 0.580×1 + (-0.861)×1 + (-0.256) ×1 = -0.564 f(z) = 0.637 Error = 1 – 0.637 = 0.363 + = -‐0.027 0.580 -‐0.861 -‐0.256 = Changes of the error Error of next iteration
- 59. Changes of theerror 0.754 0.363
- 60.
- 61.
- 62.
- 64.
- 65.
- 66.
- 67. X Σ yf Input Output 1 feature2 feature3 X –input data y – output target Σ – summation f – activation function blue circle - bias feature1 Hidden1 Σ | f Hidden3 Σ | f Hidden4 Σ | f Hidden2 Σ | f 1
- 68. X Σ yf Input Output 1 feature2 feature3 X –input data y – output target Σ – summation f – activation function blue circle - bias feature1 Hidden1 Σ | f Hidden3 Σ | f 1
- 69. X Σ yf Input Output 1 feature2 feature3 X –input data y – output target Σ – summation f – activation function blue circle - bias feature1 Hidden1 Σ | f Hidden3 Σ | f Hidden4 Σ | f Hidden2 Σ | f 1
- 70. X Σ yf Input Output 1 feature2 feature3 feature1 Hidden1 Σ |f Hidden3 Σ | f Hidden4 Σ | f Hidden2 Σ | f 1
- 71.
- 72. Workshop time Learningcurve Gentle introduction • What’s ML • ANN history • ANN overview Step by step ANN • Perceptron • Backpropagation Real world example • Sklearn example
- 73.
- 76.
- 79. If you wantto learn more … hp://dlab.berkeley.edu/training
- 80. Some useful resources • hp://iamtrask.github.io/2015/07/12/basic-‐python-‐network/ • hps://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html • hp://sebasXanraschka.com/ArXcles/2015_singlelayer_neurons.html • hp://www.emergentmind.com/neural-‐network • hp://neuralnetworksanddeeplearning.com/ • hps://www.coursera.org/learn/neural-‐networks You can also find most of today’s workshop material on my blog: hp://qingkaikong.blogspot.com/2016/10/machine-‐learning-‐1-‐what-‐is-‐machine.html I thank all the authors of the above links, as well as a lot of the images I got from internet.
Editor's Notes
- #14 It's a mathematical construct to fit a model to historical data, and use this model to forecast the future.