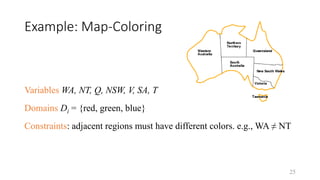
Constraint satisfaction problems (CSPs) involve assigning values to variables from given domains so that all constraints are satisfied. CSPs provide a general framework that can model many combinatorial problems. A CSP is defined by variables that take values from domains, and constraints specifying allowed value combinations. Real-world CSPs include scheduling, assignment problems, timetabling, mapping coloring and puzzles. Examples provided include cryptarithmetic, Sudoku, 4-queens, and graph coloring.

1. Constraint Satisfaction Problems (CSP)

2. Constraint satisfaction problem
A constraint satisfaction problem (CSP) requires a value, selected
from a given finite domain, to be assigned to each variable in
the problem, so that all constraints relating the variables are satisfied.
Many combinatorial problems in operational research, such as
scheduling and timetabling, can be formulated as CSPs.
2

3. Constraint satisfaction problem
CSP is one of the standard search problem where instead of saying state
is black box, we say state is defined by variables and values.
• CSP:
• state is defined by variables Xi with values from domain Di
• goal test is a set of constraints specifying allowable combinations
of values for subsets of variables
Allows useful general-purpose algorithms with more power than
standard search algorithms
3

4. Varieties of CSPs
 Discrete variables
• Finite domains:
• n variables, domain size d  O(d n) complete assignments
• e.g., 3-SAT (NP-complete)
• Infinite domains:
• integers, strings, etc.
• e.g., job scheduling, variables are start/end days for each job
• need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3
 Continuous variables
• e.g., start/end times for Hubble Space Telescope observations
• linear constraints solvable in polynomial time by linear programming
4

5. Varieties of constraints
• Unary constraints involve a single variable,
• e.g., SA ≠ green
• Binary constraints involve pairs of variables,
• e.g., SA ≠ WA
• Higher-order constraints involve 3 or more variables,
• e.g., SA ≠ WA ≠ NT
Preferences (Soft Constraints): e.g. red is better than green. Need not be satisfied but
you get credit for satisfying them.
Constraint Optimization Problems.
5

6. Real-world CSPs
 Assignment problems
 e.g., who teaches what class
 Timetabling problems
 e.g., which class is offered when and where?
 Transportation scheduling
 Factory scheduling
 Hardware configuration
 Floor planning
Notice that many real-world problems involve real-valued variables.
6

7. Examples of CSPs
1. Graph/ Map Coloring
2. Sudoku Problems
3. Cryptarithmetic Problems
4. 4- Queen Problems
5. Puzzles etc.
7

8. Example: Cryptarithmetic
Cryptarithmetic: is a type of constraint satisfaction problem in which
each alphabet and symbol is associated with unique digit.
Rules:
1. Each alphabet has unique digit
2. Digit ranges from 0- 9
3. Only one carry should be found
4. Can be solved from both sides.
8

9. Example: Cryptarithmetic
+
S E N D
M O R E
M O N E Y
9
Constraints
1. Every letter must have a digit.
2. Each letter must have different digit
𝑉𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠, 𝑋 = 0 {𝑆, 𝐸, 𝑁, 𝐷, 𝑀, 𝑂, 𝑅, 𝑌0}
𝐷𝑜𝑚𝑎𝑖𝑛𝑠, 𝐷 (𝑒𝑥𝑐𝑒𝑝𝑡 𝑆 & 𝑀) = {0,1, 2, 3, 4, 5, 6, 7, 8, 9}
𝐶𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠: 𝐴𝑙𝑙𝑑𝑖𝑓(𝑆, 𝐸, 𝑁, 𝐷, 𝑀, 𝑂, 𝑅, 𝑌)0
𝐷𝑜𝑚𝑎𝑖𝑛𝑠, 𝐷 (𝑆 & 𝑀) = {1, 2, 3, 4, 5, 6, 7, 8, 9}

10. Example: Cryptarithmetic
10
+
+
S E N D
M O R E
M O N E Y
Character Code
S
E
N
D
M
O
R
Y

11. 11
+
1
+
S E N D
M O R E
M O N E Y
Character Code
S
E
N
D
M
O
R
Y

12. 12
+ 1
1
+
S E N D
M O R E
M O N E Y
Character Code
S
E
N
D
M 1
O
R
Y

13. 13
+
9
1
1 0
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O
R
Y

14. 14
+
9
1 0
1 0
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O 0
R
Y

15. 15
+
9 ?
1 0
1 0 N
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O 0
R
Y
E + 0 = N

16. 16
+
9 E
1 0
1 0 N
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O 0
R
Y
1 CARRY FROM HERE
Expression: E + 1 = N ( N & E differ by 1 )

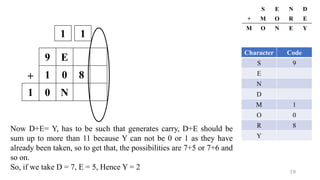
17. 17
+
9 E
1 0
1 0 N
+
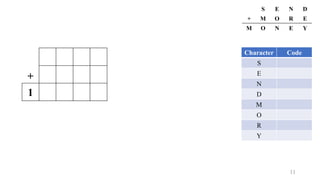
S E N D
M O R E
M O N E Y
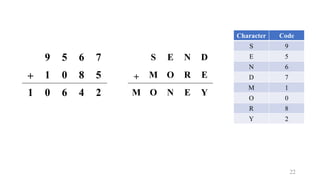
Character Code
S 9
E
N
D
M 1
O 0
R
Y
1
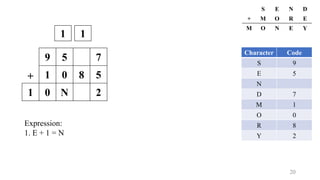
Expression:
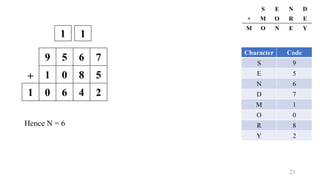
1. E + 1 = N [ N & E differ by 1 ]
2. N + R (+1) = E + 10 [ (+1) will be considered only if needed ]

18. 18
+
9 E
1 0
1 0 N
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O 0
R 8
Y
1
Expression:
1. E + 1 = N [ N & E differ by 1 ]
2. N + R (+1) = E + 10 [ (+1) will be considered only if needed ]
Substituting the values:
E + 1 + R (+1) = E + 10
Hence, R (+1) = 9
If we do not consider carry then
R must be 9 but which is not
possible because 9 has already
taken, so R might be 8.

19. 19
+
9 E
1 0 8
1 0 N
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E
N
D
M 1
O 0
R 8
Y
1 1
Now D+E= Y, has to be such that generates carry, D+E should be
sum up to more than 11 because Y can not be 0 or 1 as they have
already been taken, so to get that, the possibilities are 7+5 or 7+6 and
so on.
So, if we take D = 7, E = 5, Hence Y = 2

20. 20
+
9 5 7
1 0 8 5
1 0 N 2
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E 5
N
D 7
M 1
O 0
R 8
Y 2
1 1
Expression:
1. E + 1 = N

21. 21
+
9 5 6 7
1 0 8 5
1 0 6 4 2
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E 5
N 6
D 7
M 1
O 0
R 8
Y 2
1 1
Hence N = 6

22. 22
+
9 5 6 7
1 0 8 5
1 0 6 4 2
+
S E N D
M O R E
M O N E Y
Character Code
S 9
E 5
N 6
D 7
M 1
O 0
R 8
Y 2

23. Example: Sudoku
𝑋1 𝑋2 𝑋3
𝑋4 𝑋5 𝑋6
𝑋7 𝑋8 𝑋9
23
Constraints
• Each box contains only unique values
• Same values can not be on multiple place on
sudoku box
𝑉𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 ∶ 𝑋𝑖 = {𝑋1, 𝑋2, 𝑋3, 𝑋4, 𝑋5, 𝑋6, 𝑋7, 𝑋8, 𝑋9}
𝐷𝑜𝑚𝑎𝑖𝑛𝑠: 𝐷𝑖 = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Solution of this CSP is : {𝑋𝑖} = {𝐷𝑖}
𝐶𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠: 𝐴𝑙𝑙𝑑𝑖𝑓(1, 2, 3, 4, 5, 6, 7, 8, 9)0

24. Example: 4-Queens
• States: 4 queens in 4 columns (44 = 256 states)
• Actions: move queen in column
• Goal test: no attacks
• Evaluation: h(n) = number of attacks
24

25. Example: Map-Coloring
25
Variables WA, NT, Q, NSW, V, SA, T
Domains Di = {red, green, blue}
Constraints: adjacent regions must have different colors. e.g., WA ≠ NT

26. Example: Map-Coloring
26
Solutions are complete and consistent assignments, e.g., WA = red,
NT = green, Q = red, NSW = green, V = red, SA = blue, T = green

27. Thank You
27