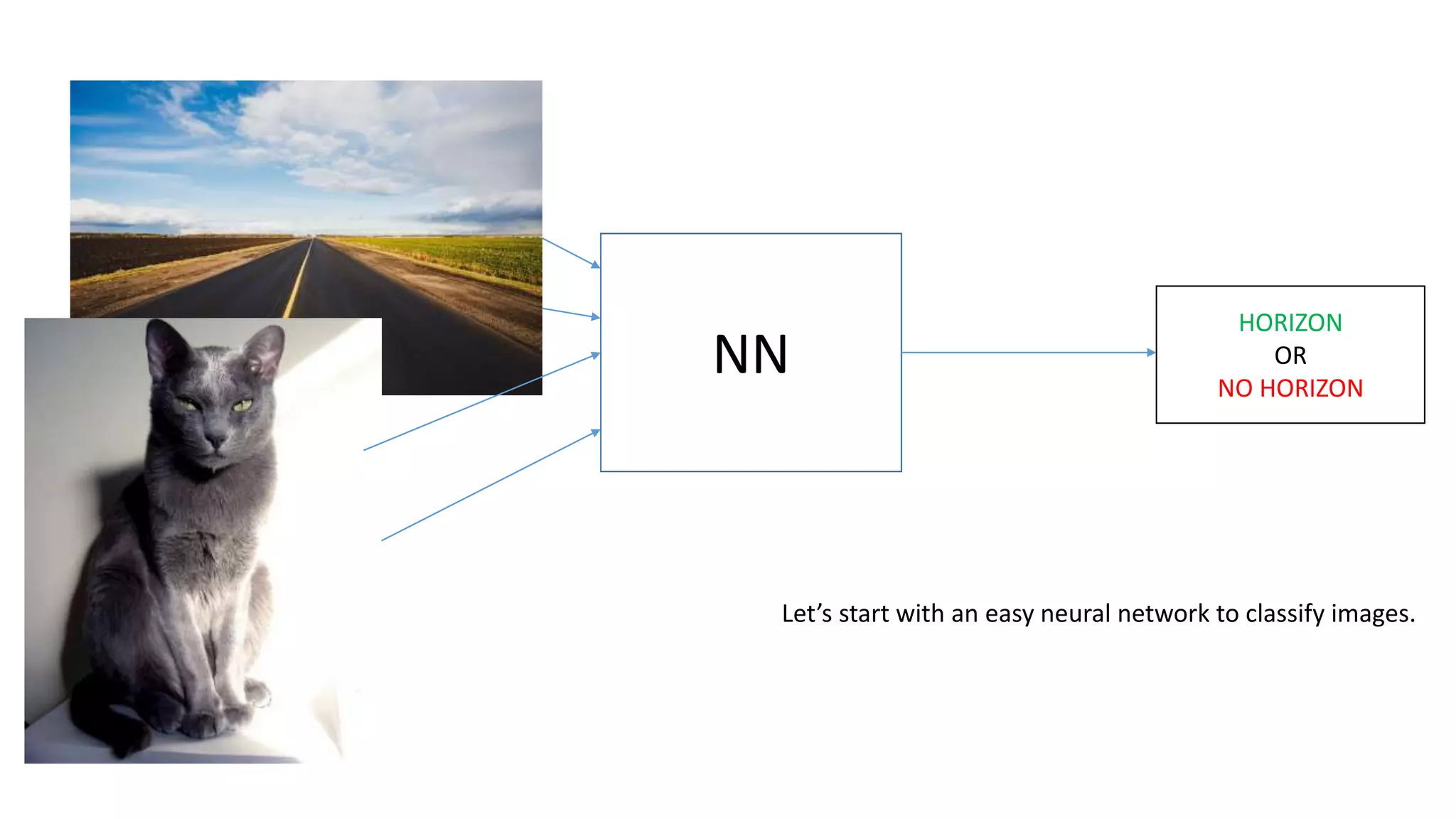
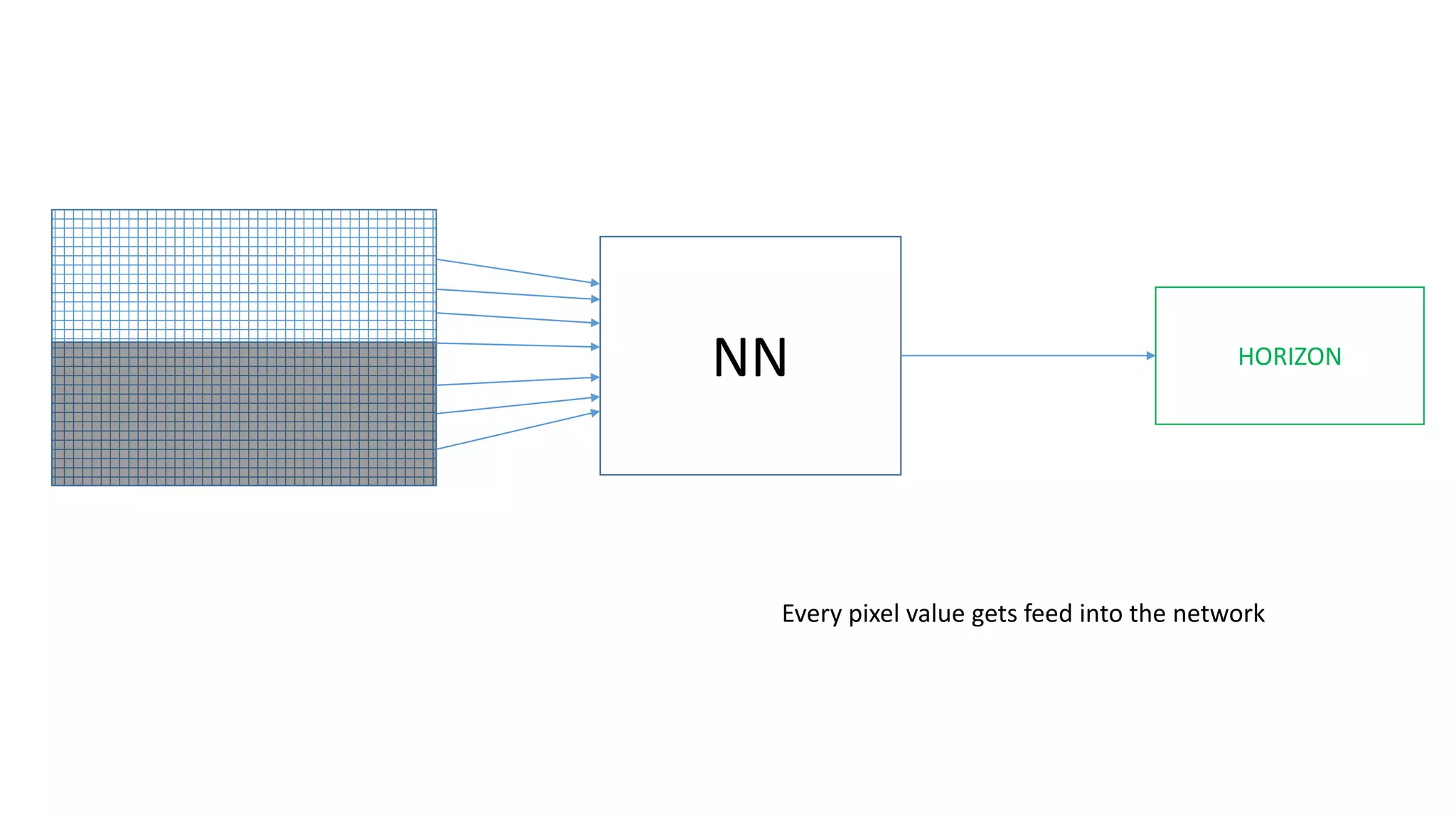
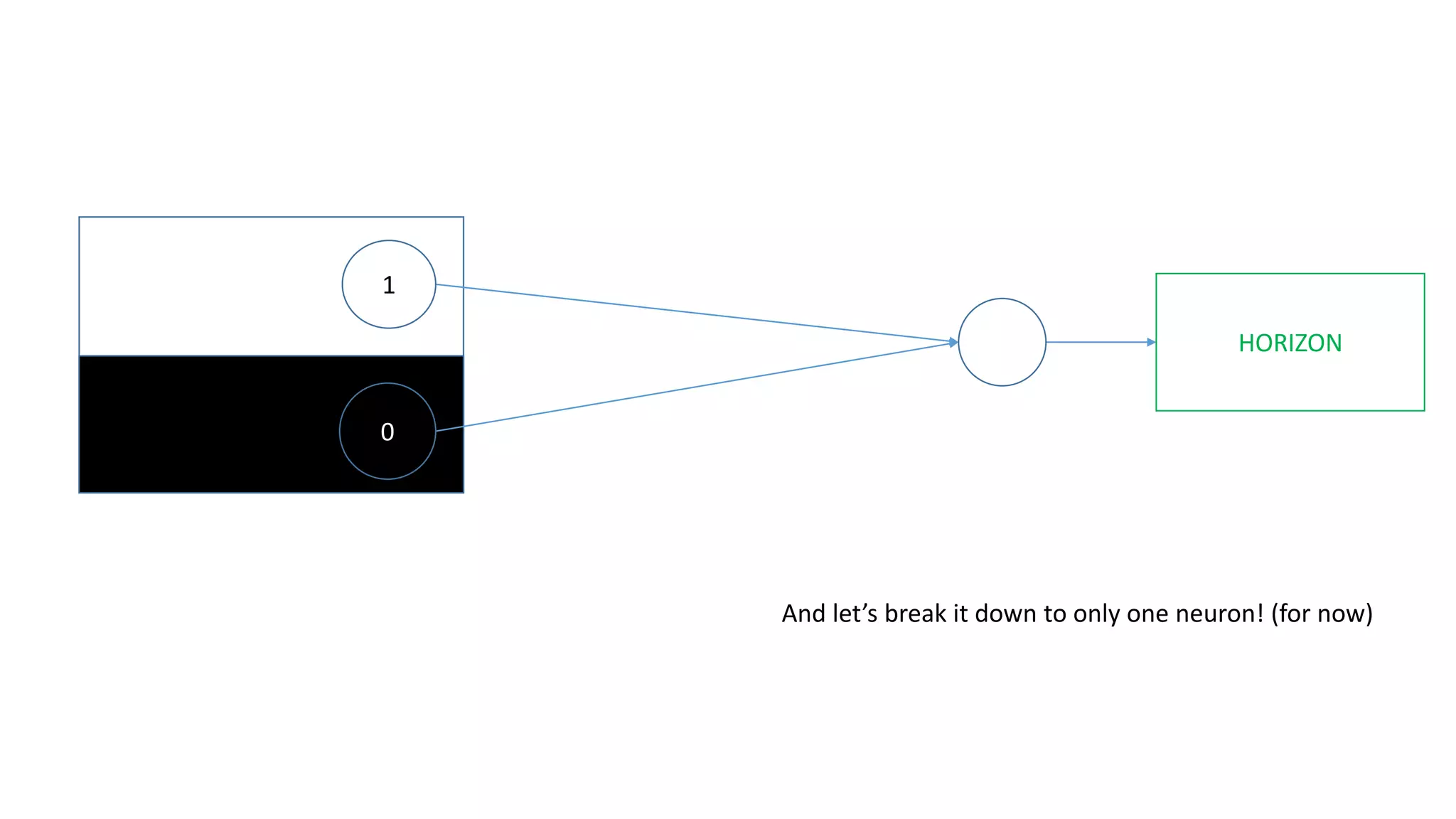
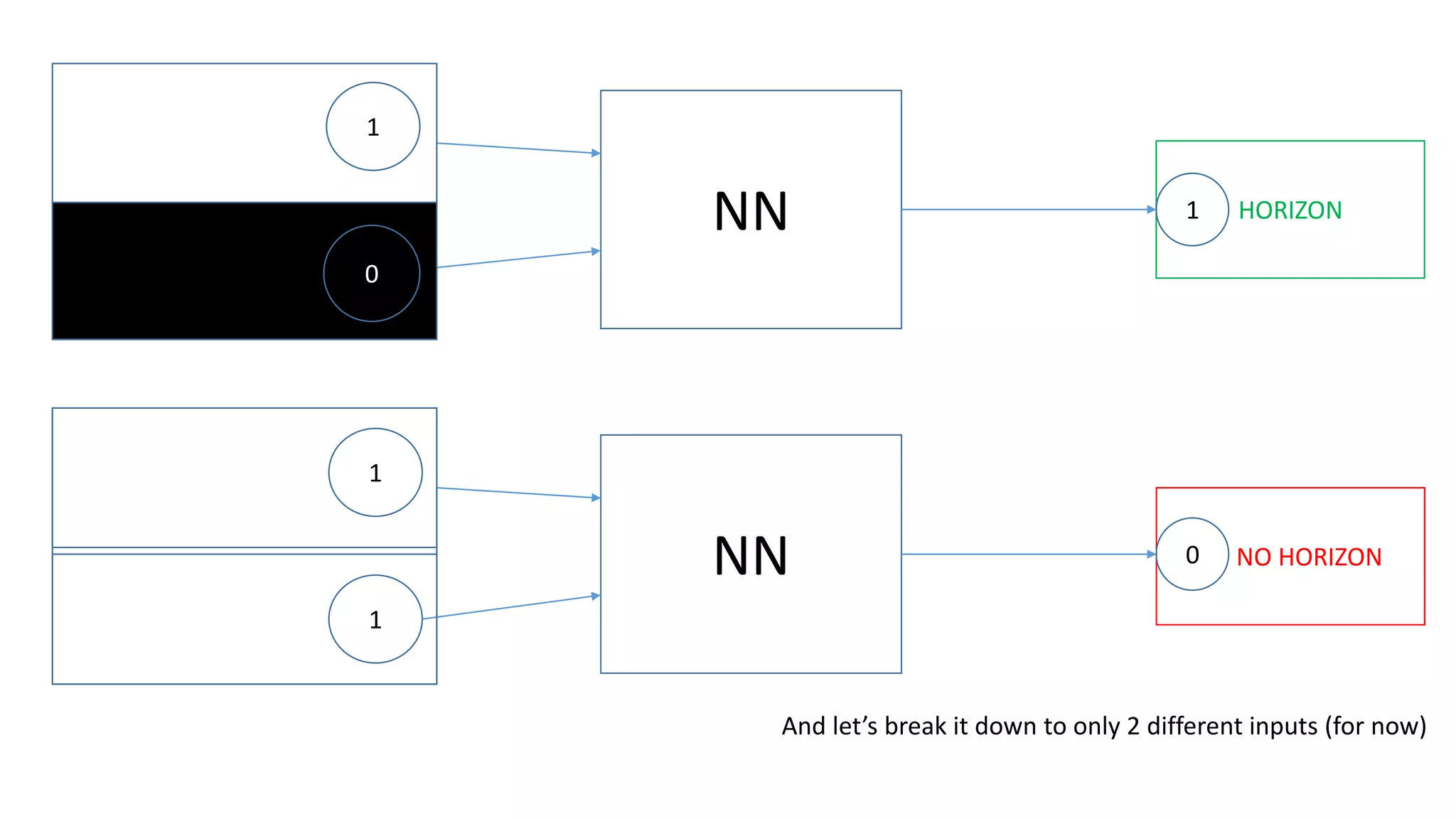
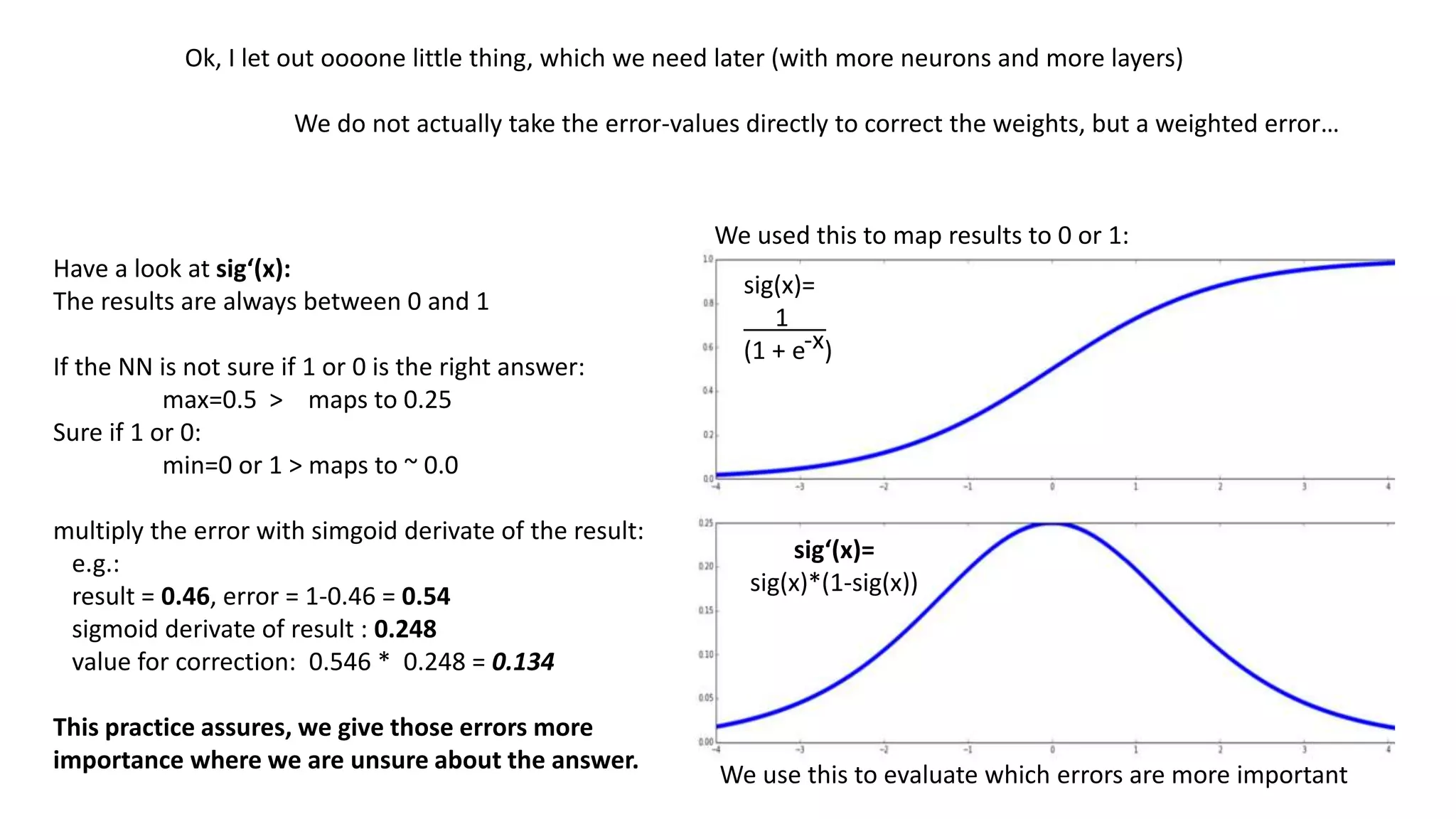
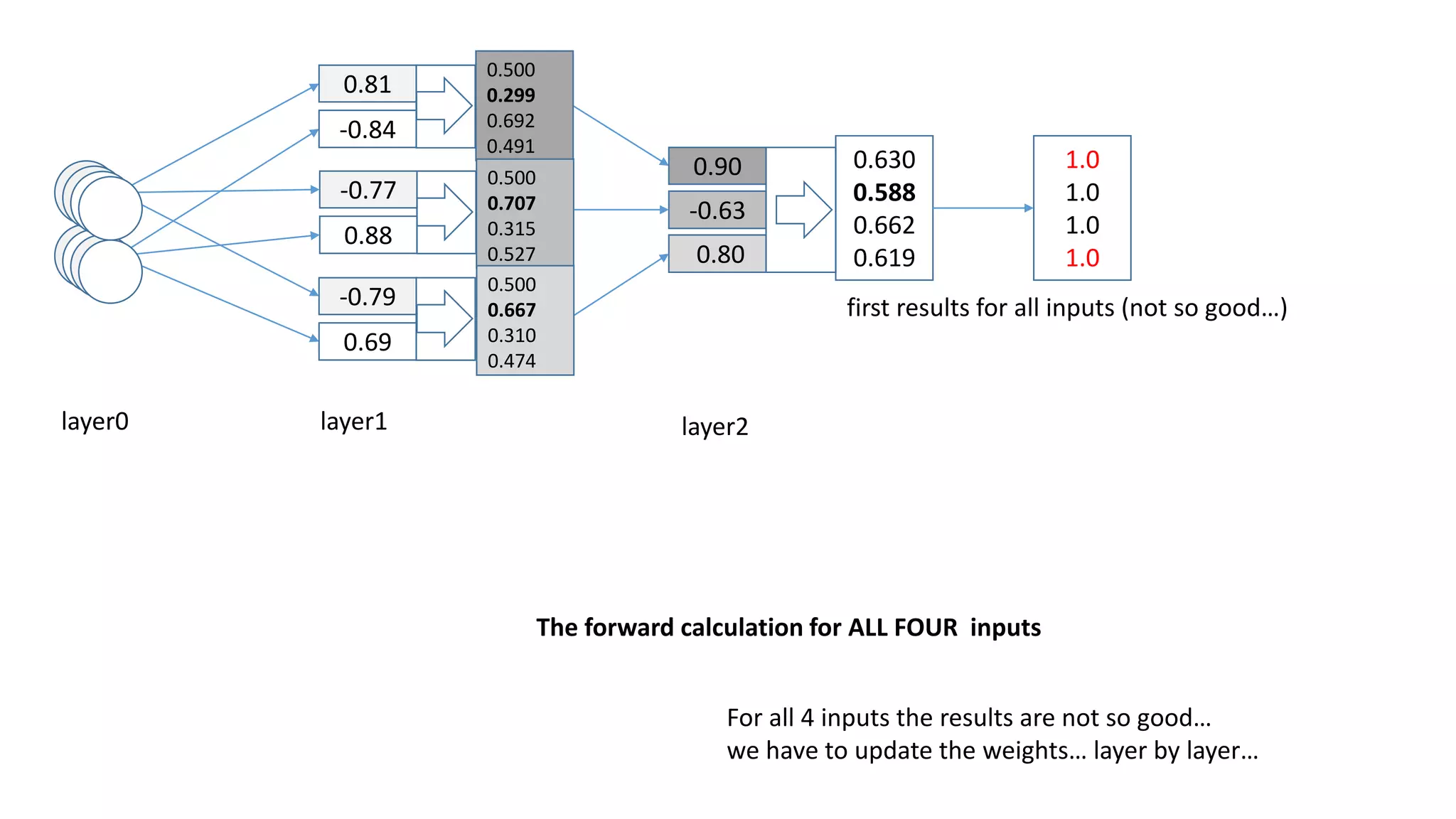
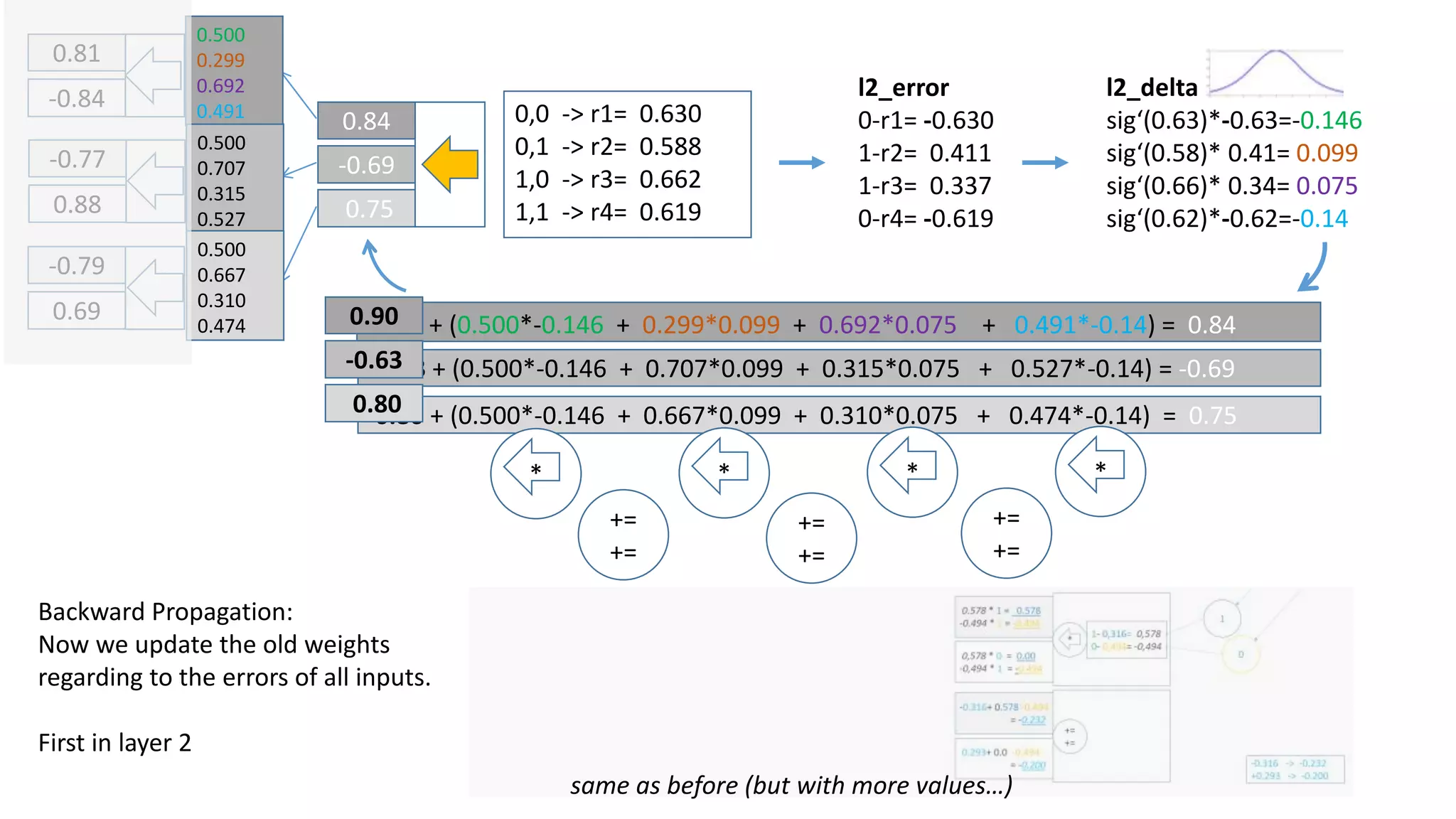
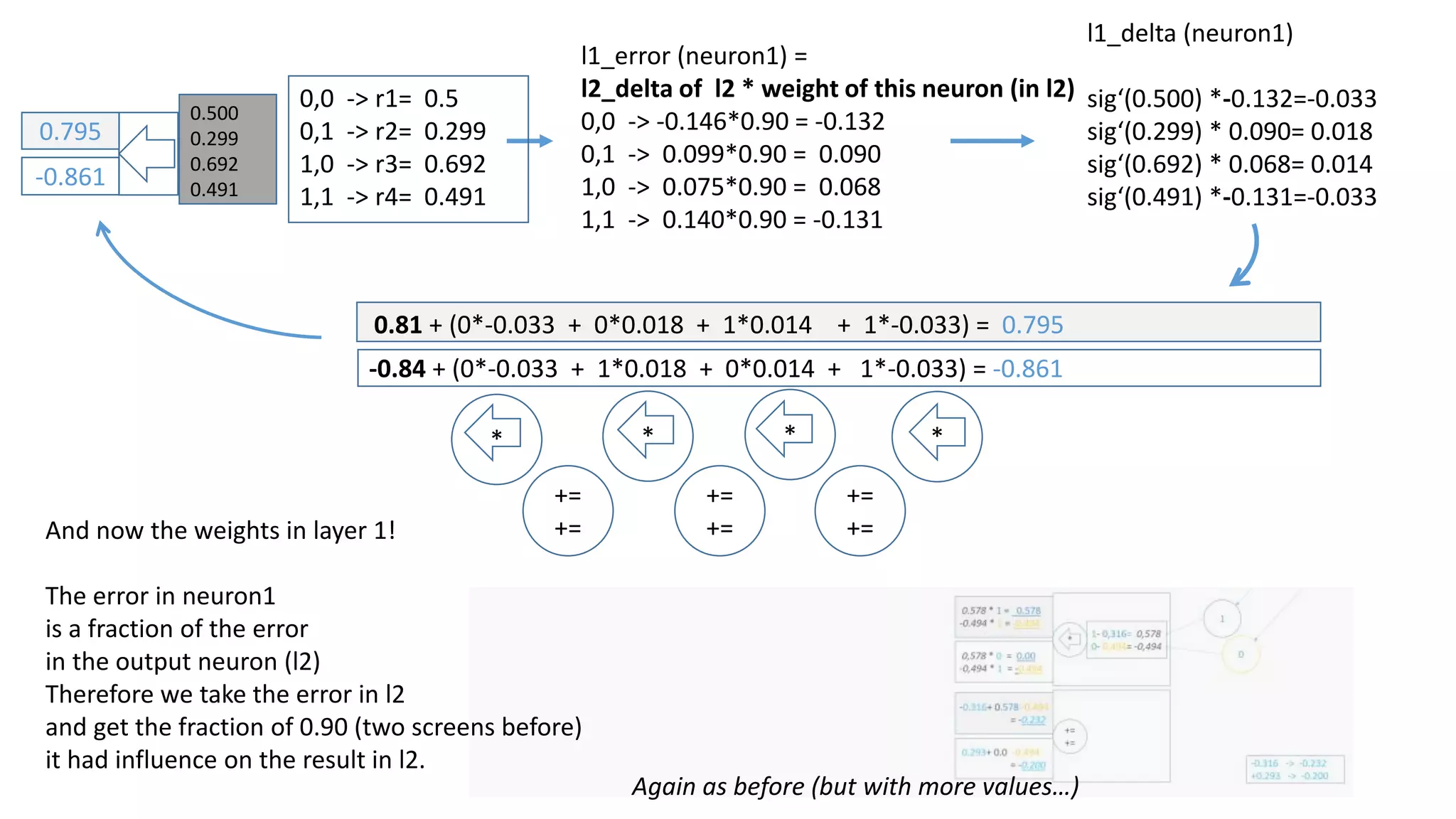
The document explains the functioning of a neural network in a simplified manner, focusing on how inputs are processed through neurons to produce outputs. It describes the concepts of weights, calculations, the sigmoid function, error adjustment, and backpropagation, using examples with pixel inputs for classification. The text highlights the iterative nature of training neural networks, including the necessity of multiple layers to successfully handle complex functions like XOR.

1. How does a neural network
work
… literally!
I mean, … really literally!
Don’t give me the formulas,
Don’t give me the python code
JUST GIVE ME THE NUMBERS!
Ok, here it is ….

2. NN
HORIZON
OR
NO HORIZON
Let’s start with an easy neural network to classify images.

3. NN HORIZON
Every pixel value gets feed into the network

4. HORIZON
At Wikipedia you find images like these, which show, that
Every pixel value is feed into every neuron.
Looks complicated! But the math is actually not that hard.
It’ just a lot of calculations! So let’s break it down.

5. HORIZON
1
0
Let’s focus on images with two pixels only. (for now)

6. HORIZON
1
0
And let’s break it down to only one neuron! (for now)

7. 1
0
1
For every input we have a wanted outcome.
here it is 1,0 -> 1
At first we do not know, what outcome
the neural net will be calculating.
?

8. 1
0
1
* -0.16
* 0.99
Random Weights
To start with the calculations, we set some random
weights for the different inputs.
These can be any numbers, but mostly one starts
in the range of -1 to 1.
With these we calculate our first inputs to the neuron.
?
= -0.16
= 0.00

9. 1
0
1
* -0.16
* 0.99
Random Weights
Then we add up the results for every weight.
?
= -0.16
= 0.00
+ -0.16

10. 1 * -0.16 = -0.16
0 * 0.99 = 0.0
1
0
+ -0.16 > 0,46 0 1
Then we do one “higher math” step (not really), and get out 0,46
(Actually we just put -0.16 as x into the sigmoid-function,
which is explaind the next slide and might look complicated
but really isn’t.)
0,46 rounds to 0 which which is wrong … (we wanted 1)
But that’s all there is to get results from a neural network
that’s all there is in a neuron!

11. 1 * -0.16 = -0.16
0 * 0.99 = 0.0
1
0
+ -0.16 > 0,46 0 1
Example Input: Output:
-1000 0.0
-100 0.0
-10 0.00004
-5 0.0066
-1 0.2689
-0.75 0.3208
-0.25 0.4378
0.0 0.5
0.25 0.5621
0.75 0.6791
1 0.7310
5 0.9933
10 0.9999
100 1.0
1000 1.0
The “higher math”:
With the sum of the weighted inputs (-0.16)
-> we call the sigmoid-function(x)
Whoohooo!
But what it does, is actually pretty easy: It maps every
input to a value between 0 and 1 (see examples left)
When we put -0.16 into the function we get 0.46 as a
result. If we round this value we get 0 as an outcome of
our neuron. This is wrong!
What to do? Change the weights!

12. 1 * -0.16 = -0.16
0 * 0.99 = 0.0
1
0
+ -0.16 > 0,46 0
0.546 * 1 = 0.546
0.546 * 0 = 0.0
* 1- 0,46 = 0,546 1
1
-0.16+-0.546 = 0.38
0.99 + 0.0 = 0,99
+=
+=
0.16 -> 0.38
0.99 -> 0.99
New weights:
To correct the weights, we…
…calculate the output error
(0.546)
…calculate the error
per weight and input
…and add it to the old weight.
That’s called “Backpropagation”
(because it goes backwards)

13. 1 * 0.38 = 0.38
0 * 0.99 = 0.0
+ 0.38 > 0,59 1
1
0
AND THAT‘s IT!
Well… basically it really is.
It‘s all about getting input values to the right output values
by adjusting the weights.
But obviously neural nets have more than one neuron.
And normally there is more than one input.
Let‘s increase the input‘s first!
Now we calculate again, and get the right output!

14. 1
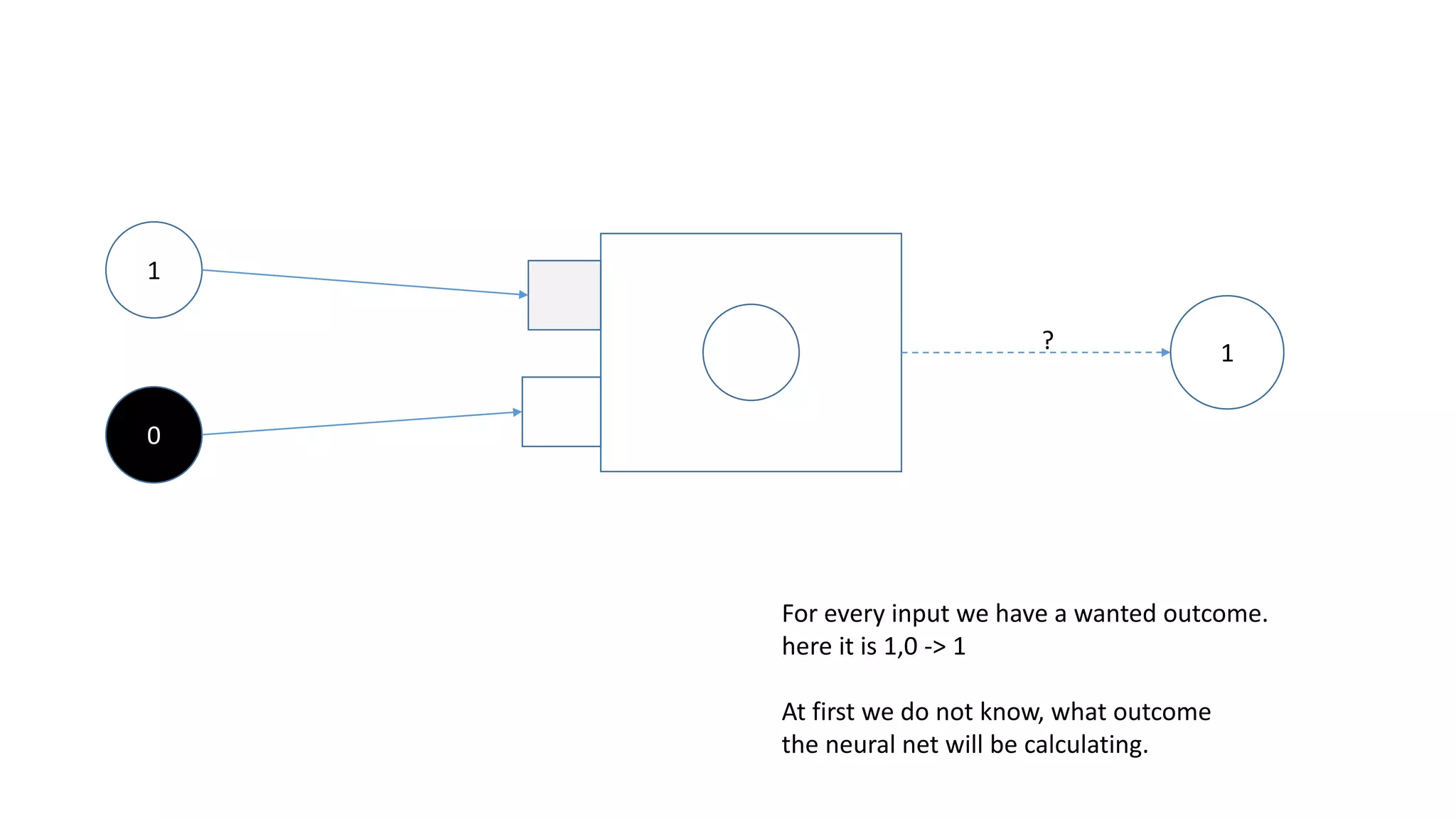
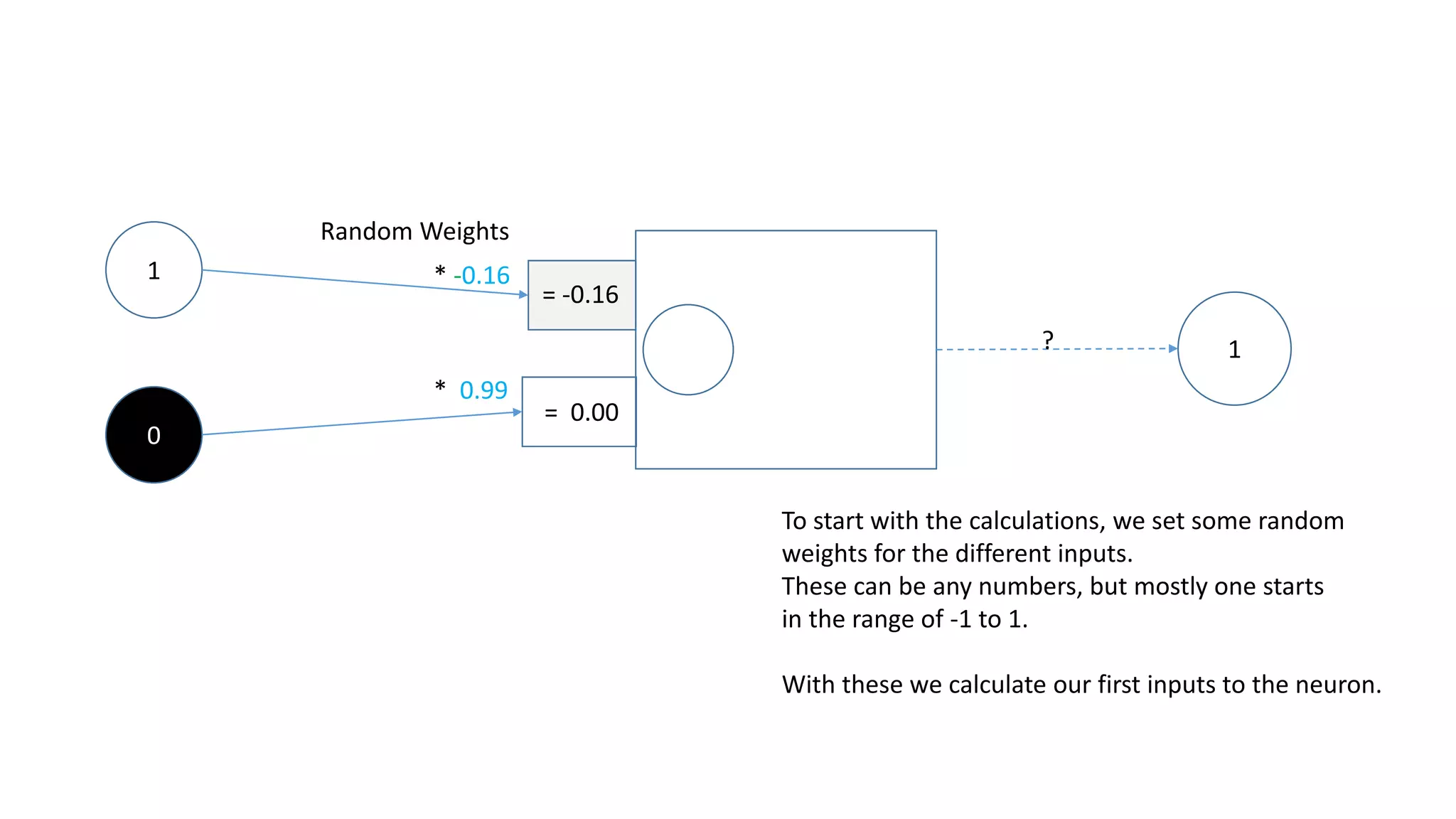
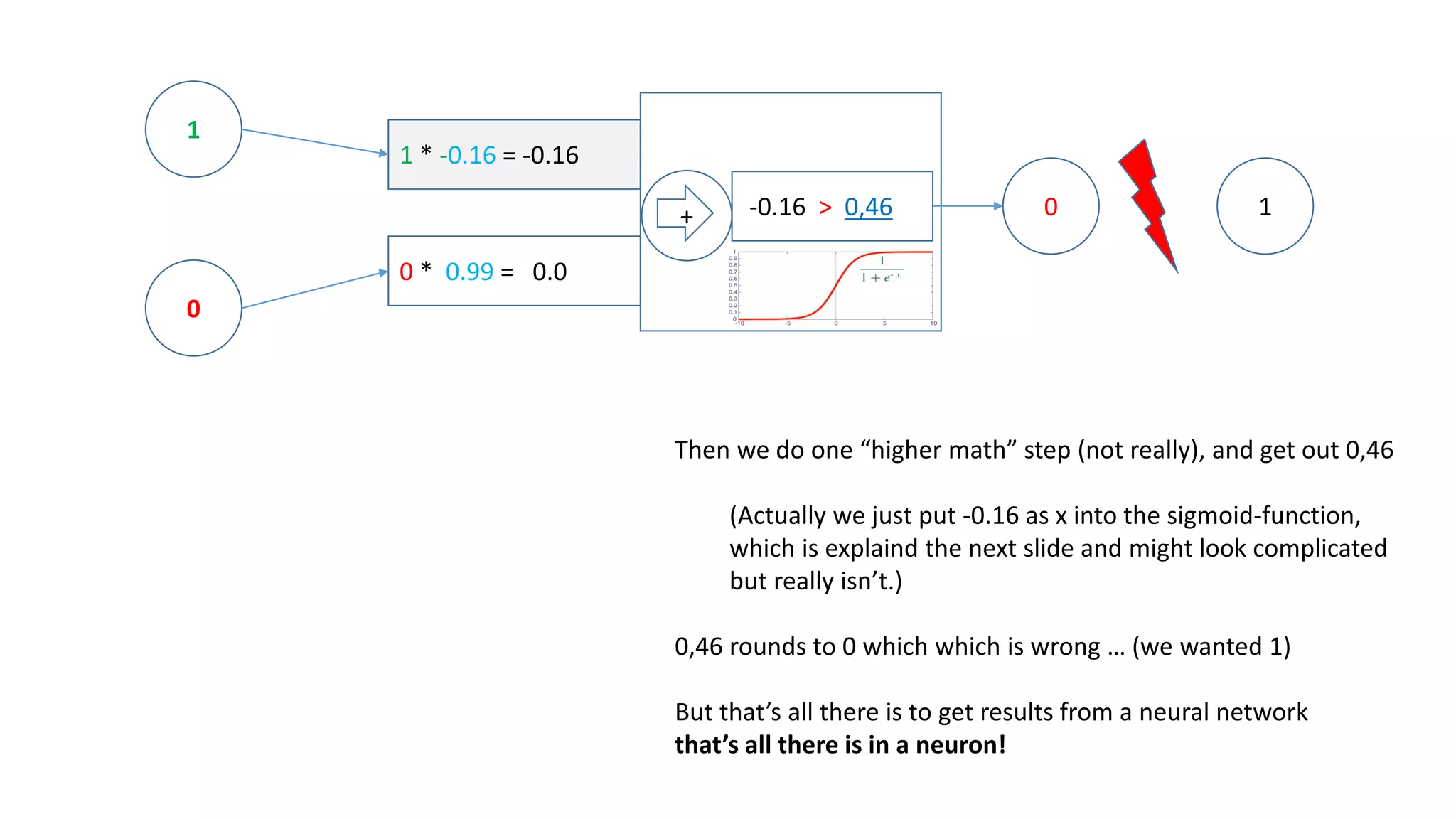
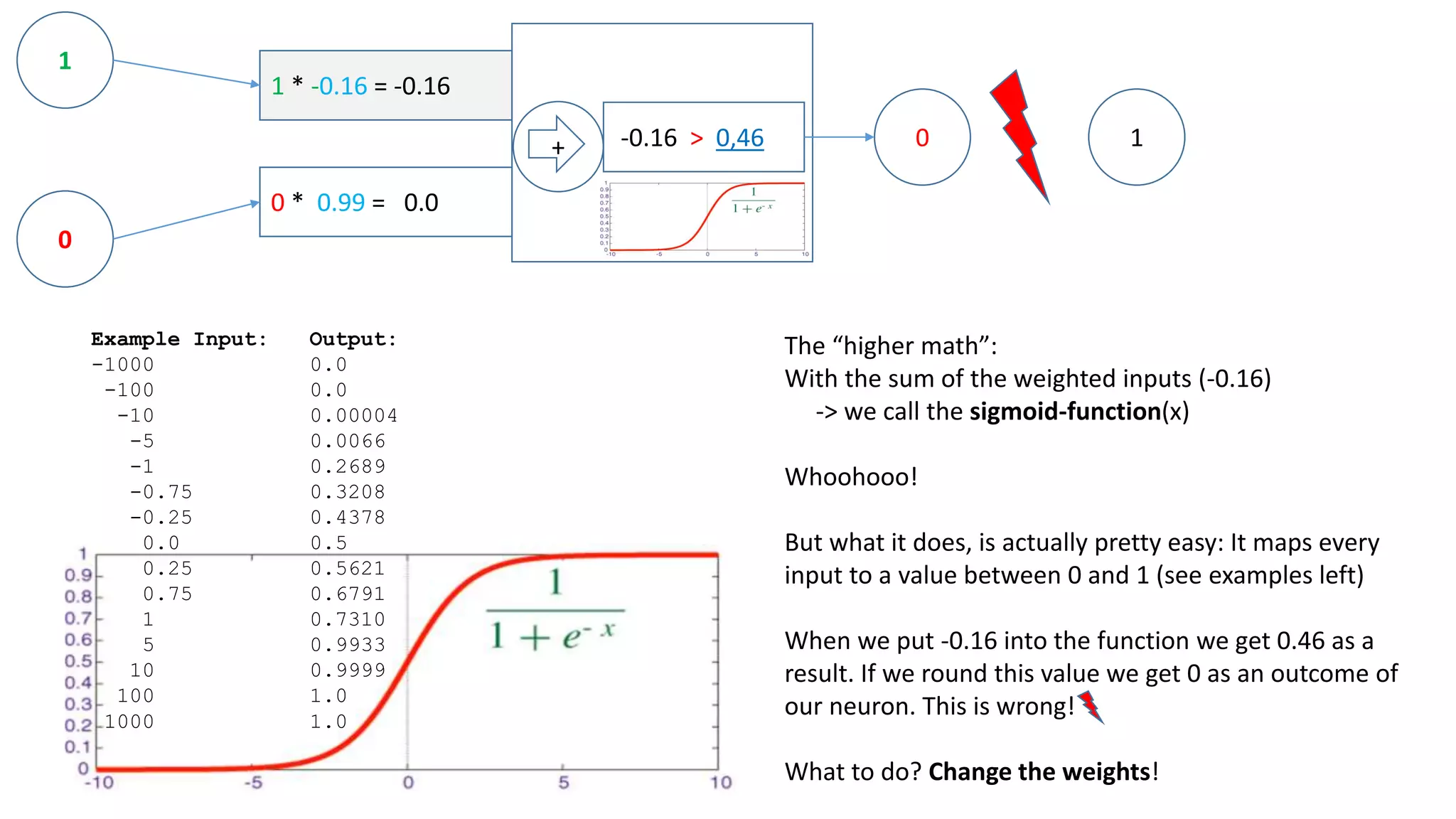
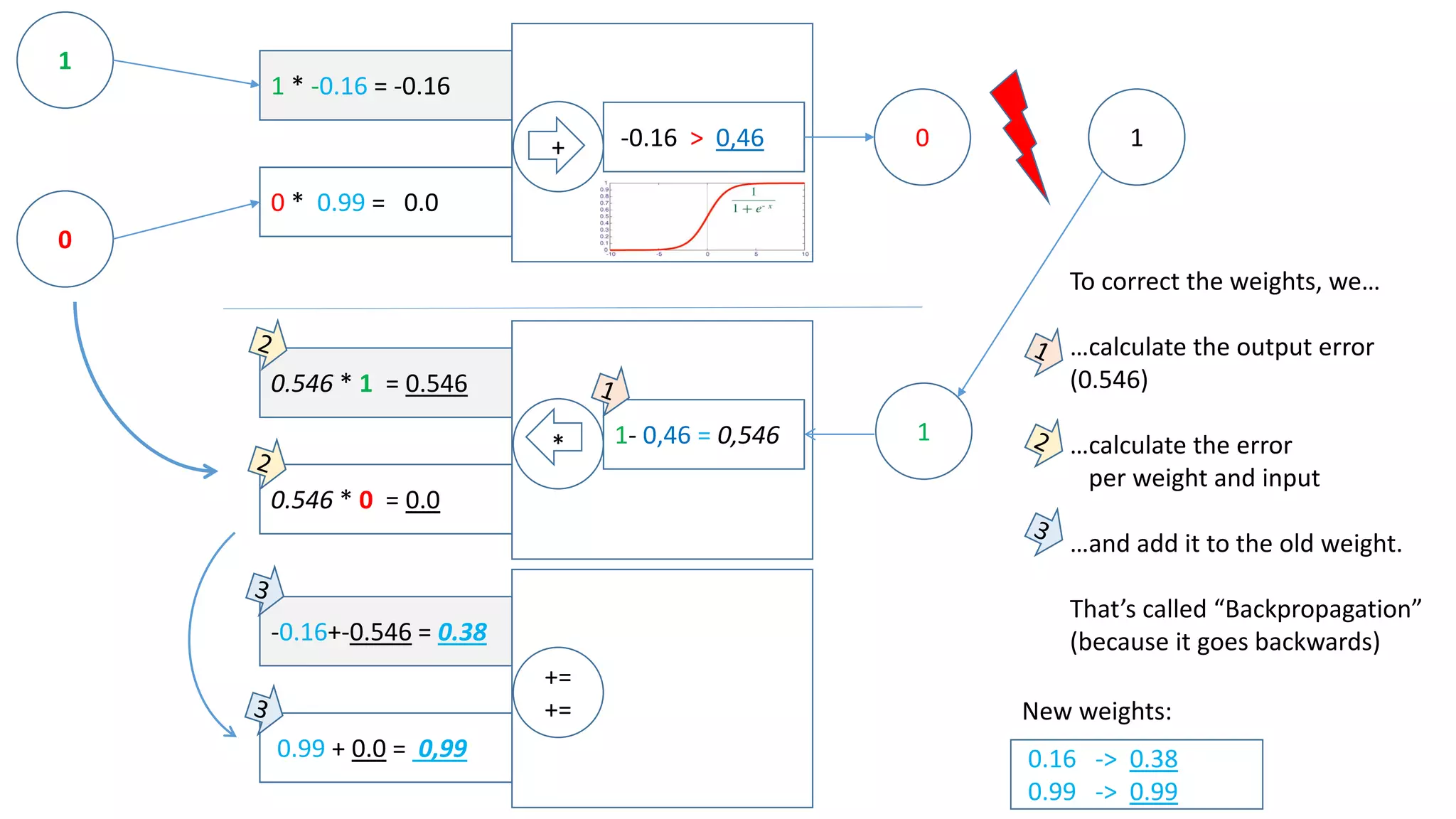
1
0
1
0
1
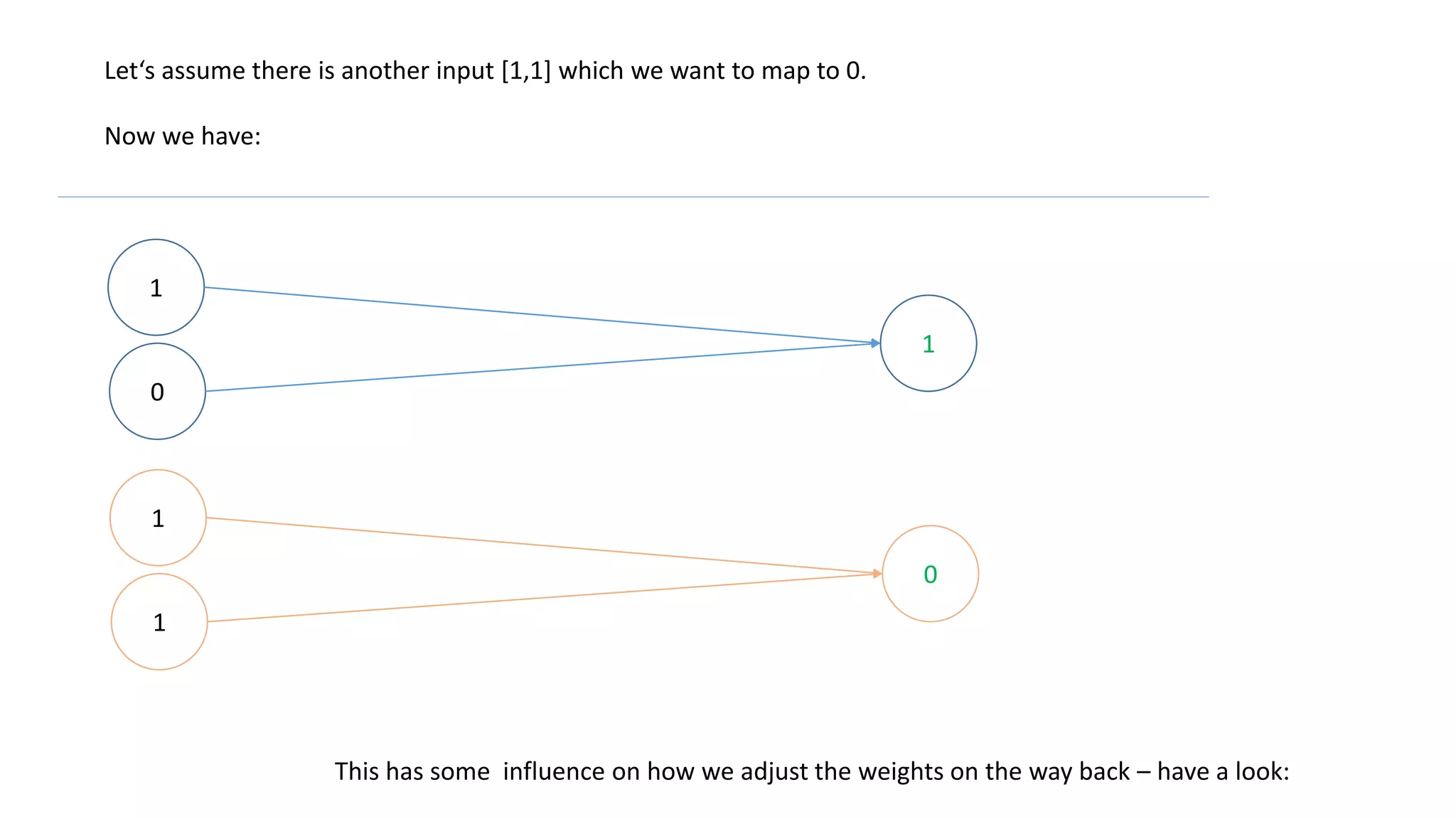
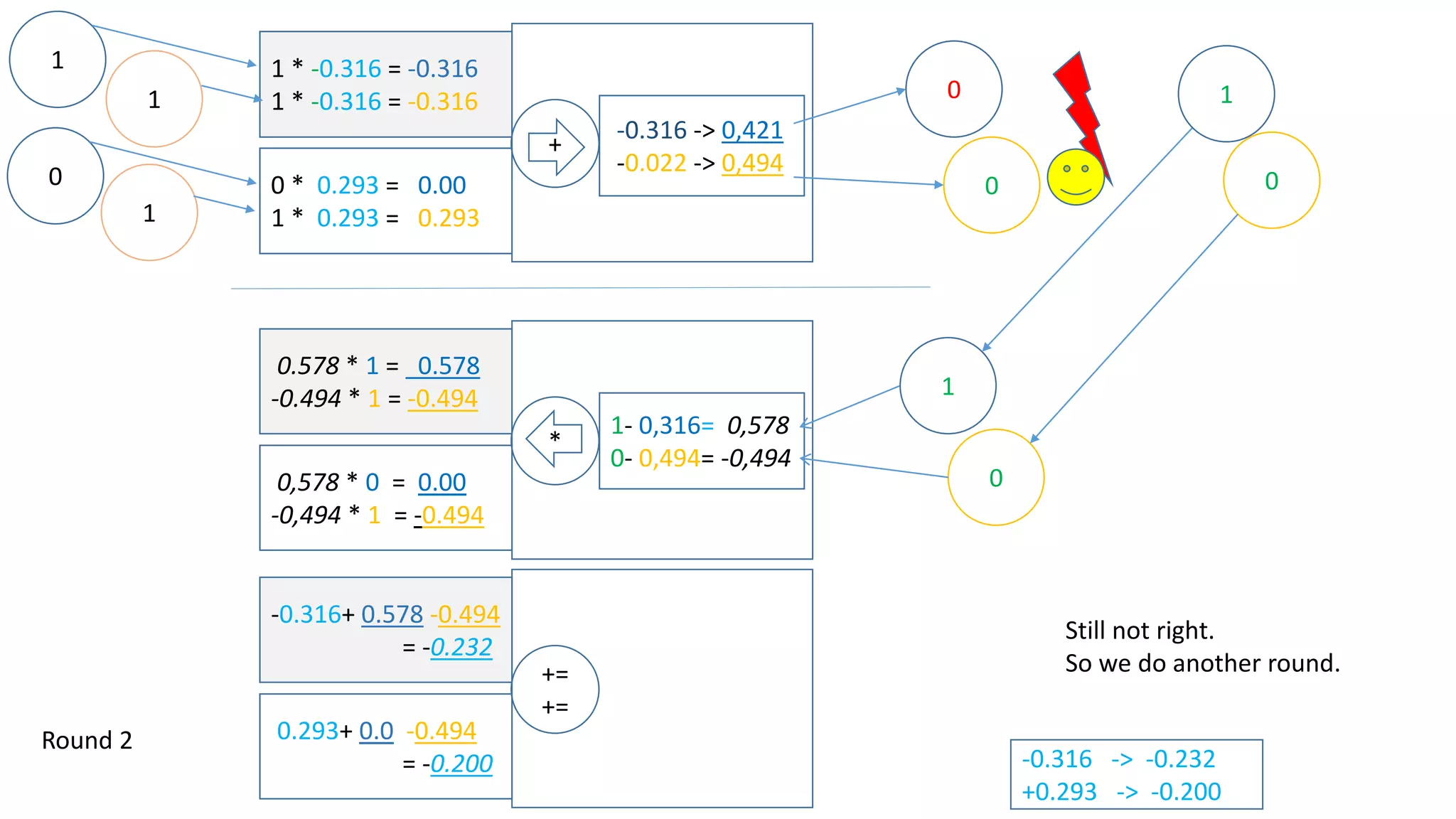
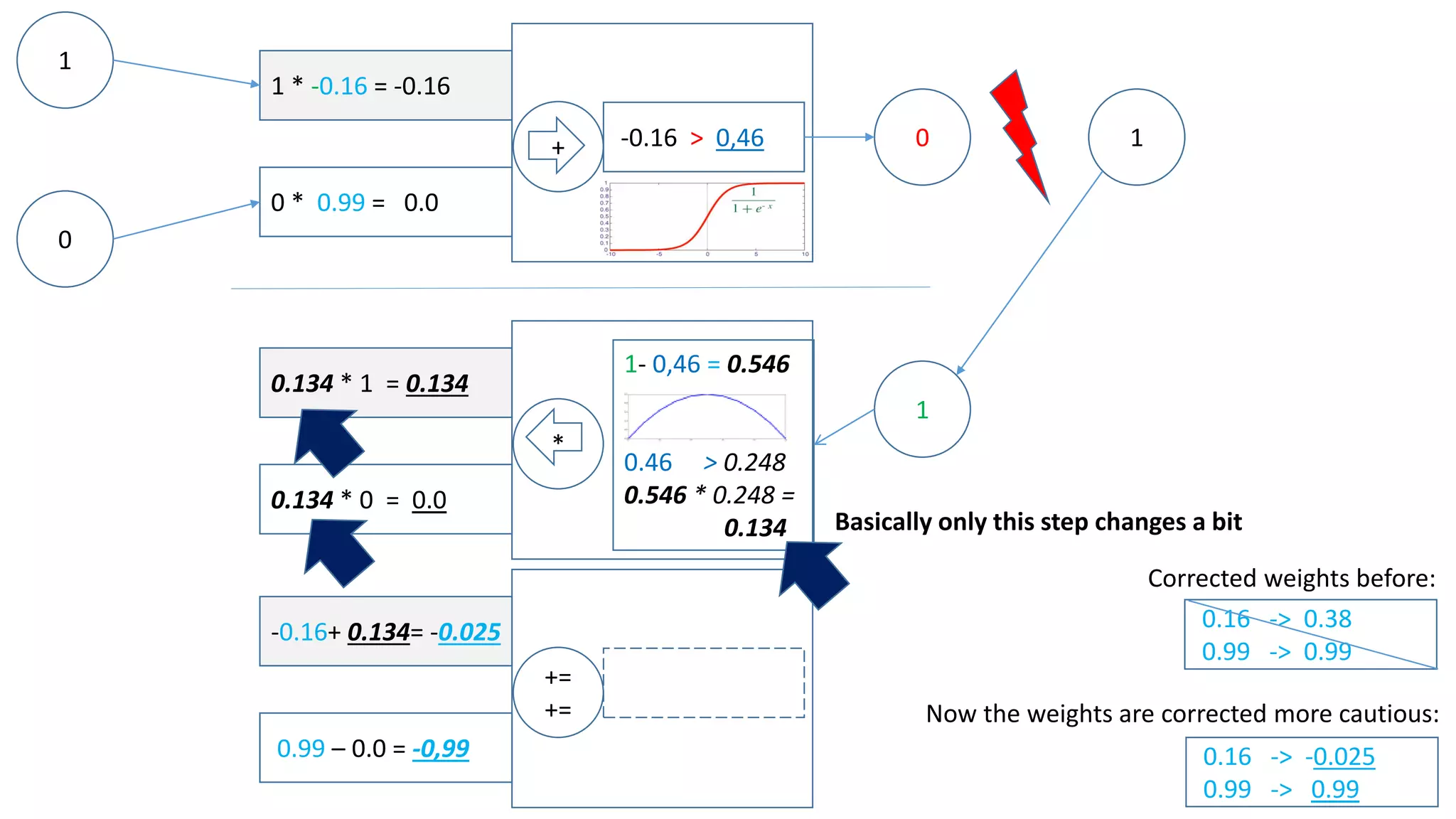
Let‘s assume there is another input [1,1] which we want to map to 0.
Now we have:
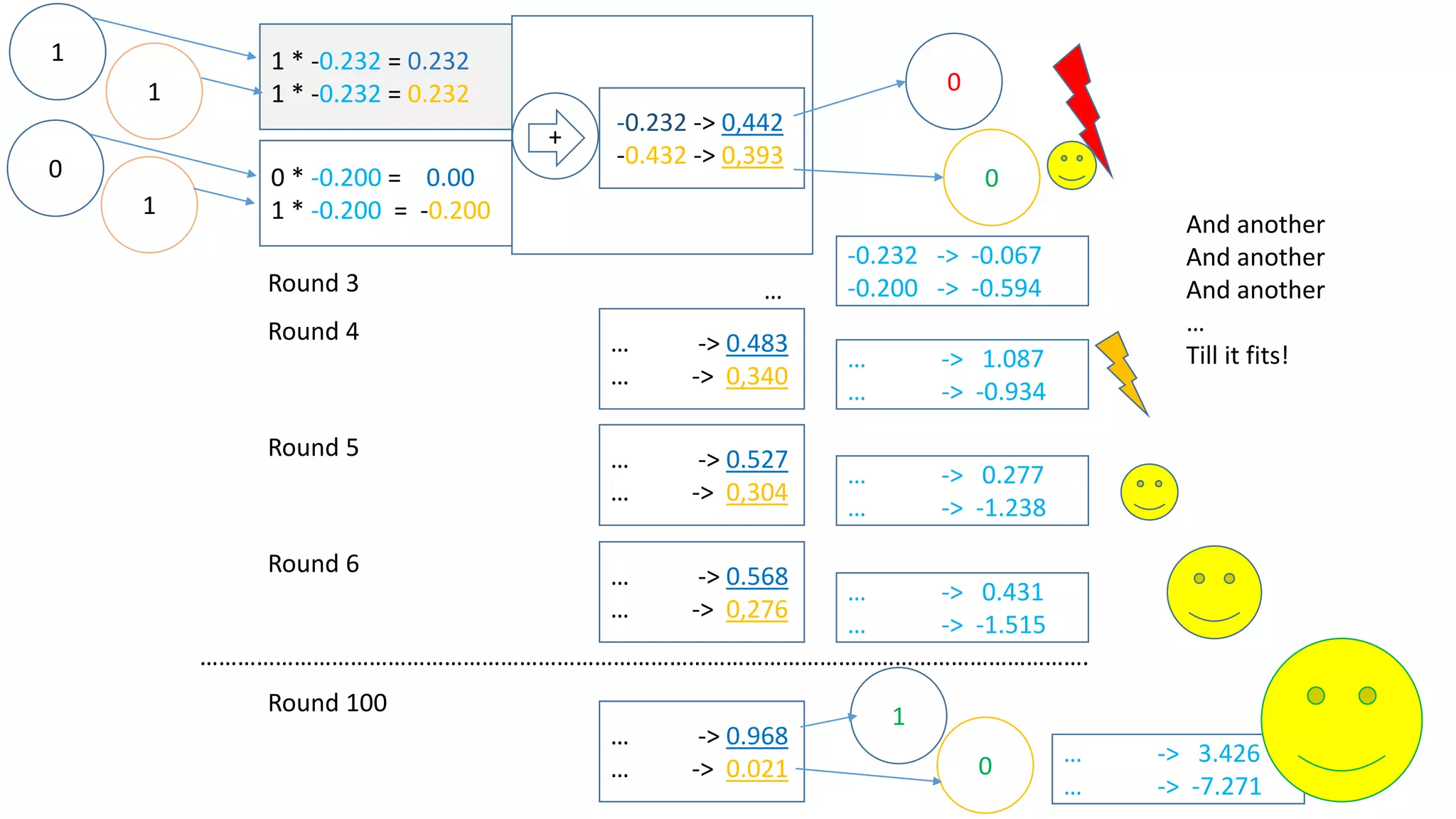
This has some influence on how we adjust the weights on the way back – have a look:

15. 1 * -0.16 = -0.16
1 * -0.16 = -0.16
0 * 0.99 = 0.00
1 * 0.99 = 0.99
1
0
+
-0.16 -> 0.460
0.83 -> 0.696
0
0.546 * 1 = 0.546
-0.696 * 1 = -0.696
0.546 * 0 = 0.0
-0.696 * 1 = -0.696
*
1- 0.460= 0.546
0- 0.696= -0.696
1
-0.16+ 0.546 -0.696
= -0.316
0.99+ 0.0 -0.696
= +0.293
+=
+=
1
1
1 0
0
1
0.16 -> -0.316
0.99 -> +0.293
Round 1
Now it‘s 2 values to add here…:
We do the same for both inputs
All what changes is how we
sum up the new weight

16. -0.16 + (1 * -0.546 + 1 * -0.696) = -0.16 + 0.546 - 0.696 = -0.316
We can write this update regarding to the errors
in one line for each input weight:
0.99 + (0 * -0.546 + 1 * -0.696) = 0.99 + 0.000 - 0.696 = 0.293
0.16 -> -0.316
0.99 -> +0.293
0.546 * 1 = 0.546
-0.696 * 1 = -0.696
0.546 * 0 = 0.0
-0.696 * 1 = -0.696
*
1- 0.460= 0.546
0- 0.696= -0.696
-0.16+ 0.546 -0.696
= -0.316
0.99+ 0.0 -0.696
= +0.293
+=
+=
(we will do this again later when we have many weights…)

17. 1 * -0.316 = -0.316
1 * -0.316 = -0.316
0 * 0.293 = 0.00
1 * 0.293 = 0.293
1
0
+
-0.316 -> 0,421
-0.022 -> 0,494
0
0.578 * 1 = 0.578
-0.494 * 1 = -0.494
0,578 * 0 = 0.00
-0,494 * 1 = -0.494
*
1- 0,421= 0,578
0- 0,494= -0,494
1
-0.316+ 0.578 -0.494
= -0.232
0.293+ 0.0 -0.494
= -0.200
+=
+=
1
1
0 0
0
1
-0.316 -> -0.232
+0.293 -> -0.200
Round 2
Still not right.
So we do another round.

18. 1 * -0.232 = 0.232
1 * -0.232 = 0.232
0 * -0.200 = 0.00
1 * -0.200 = -0.200
1
0
+
-0.232 -> 0,442
-0.432 -> 0,393
01
1
0
-0.232 -> -0.067
-0.200 -> -0.594…
… -> 1.087
… -> -0.934
… -> 0.483
… -> 0,340
… -> 0.277
… -> -1.238
… -> 0.527
… -> 0,304
… -> 0.568
… -> 0,276
… -> 0.431
… -> -1.515
… -> 0.968
… -> 0.021
… -> 3.426
… -> -7.271
Round 4
Round 3
Round 5
Round 6
Round 100
…………………………………………………………………………………………………………………………….
1
0
And another
And another
And another
…
Till it fits!

19. weight 1 (started at -0.16)
weight 2 (started at 0.99)
sum of errors
the error converges to 0.0 (hopefully :-)

20. Ok, I let out oooone little thing, which we need later (with more neurons and more layers)
We do not actually take the error-values directly to correct the weights, but a weighted error…
Have a look at sig‘(x):
The results are always between 0 and 1
If the NN is not sure if 1 or 0 is the right answer:
max=0.5 > maps to 0.25
Sure if 1 or 0:
min=0 or 1 > maps to ~ 0.0
multiply the error with simgoid derivate of the result:
e.g.:
result = 0.46, error = 1-0.46 = 0.54
sigmoid derivate of result : 0.248
value for correction: 0.546 * 0.248 = 0.134
This practice assures, we give those errors more
importance where we are unsure about the answer.
sig‘(x)=
sig(x)*(1-sig(x))
sig(x)=
1
(1 + e )-x
We used this to map results to 0 or 1:
We use this to evaluate which errors are more important

21. 1 * -0.16 = -0.16
0 * 0.99 = 0.0
1
0
+ -0.16 > 0,46 0
0.134 * 1 = 0.134
0.134 * 0 = 0.0
*
1- 0,46 = 0.546
0.46 > 0.248
0.546 * 0.248 =
0.134
1
1
-0.16+ 0.134= -0.025
0.99 – 0.0 = -0,99
+=
+=
0.16 -> -0.025
0.99 -> 0.99
Now the weights are corrected more cautious:
0.16 -> 0.38
0.99 -> 0.99
Corrected weights before:
Basically only this number changes a bit

22. 1 * -0.16 = -0.16
0 * 0.99 = 0.0
1
0
+ -0.16 > 0,46 0
0.546 * 1 = 0.546
0.546 * 0 = 0.0
* 1- 0,46 = 0,546
1
1
-0.16+-0.546 = 0.38
0.99 + 0.0 = 0,99
+=
+=
0.16 -> 0.38
0.99 -> 0.99
New weights:
To correct the weights, we…
…calculate the output error
(0.546)
…calculate the error
per weight and input
…and add it to the old weight.
That’s called “Backpropagation”
(because it goes backwards)
(s. slide 12)

23. This was fun – let’s try another more complicated example with our neuron
…. XOR

24. 0
0
0
0
1
1
1
0
1
1
1
0
in out
0 0 0
0 1 1
1 0 1
1 1 0
XOR
spoiler: does not work... (with one neuron)

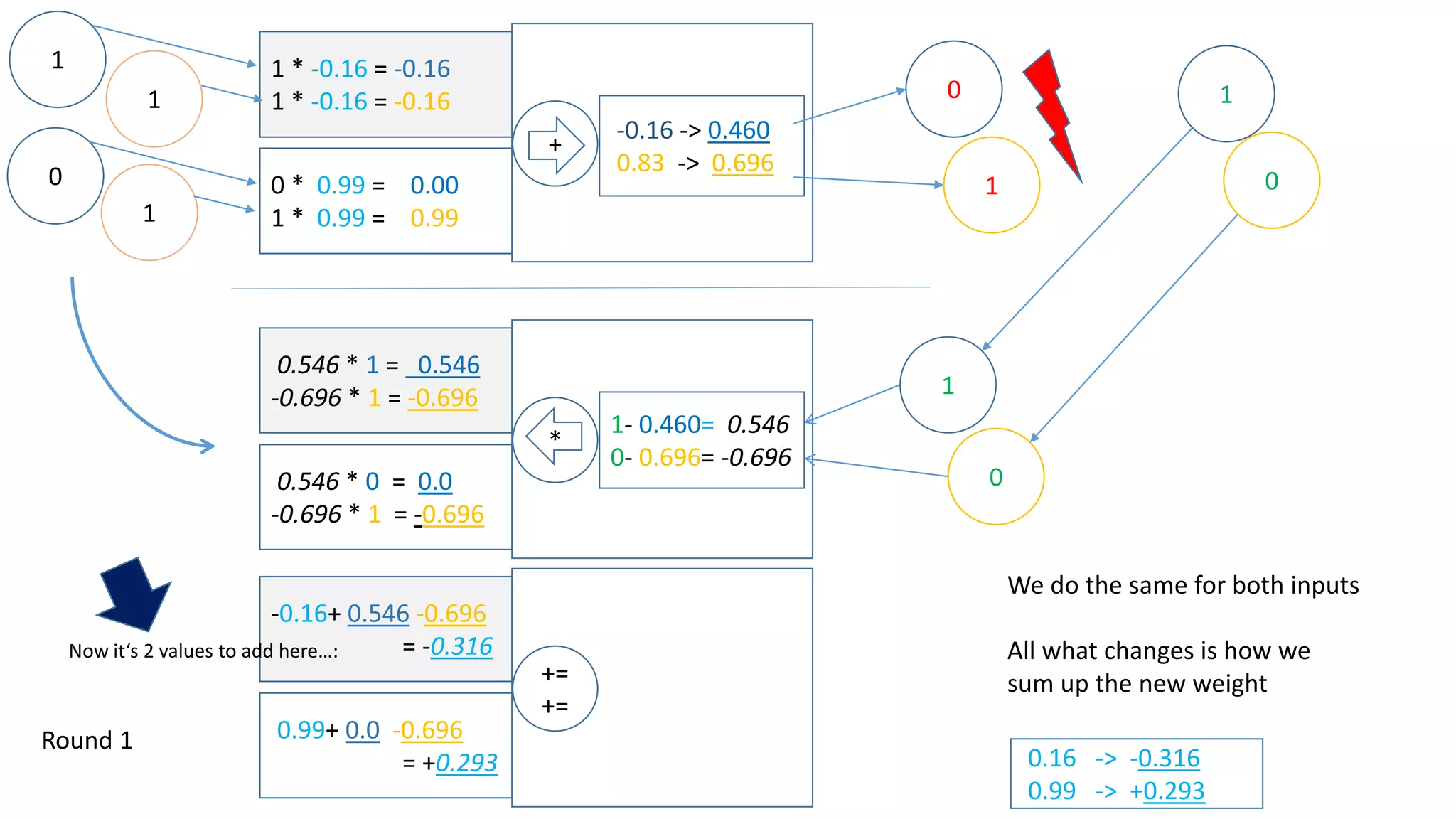
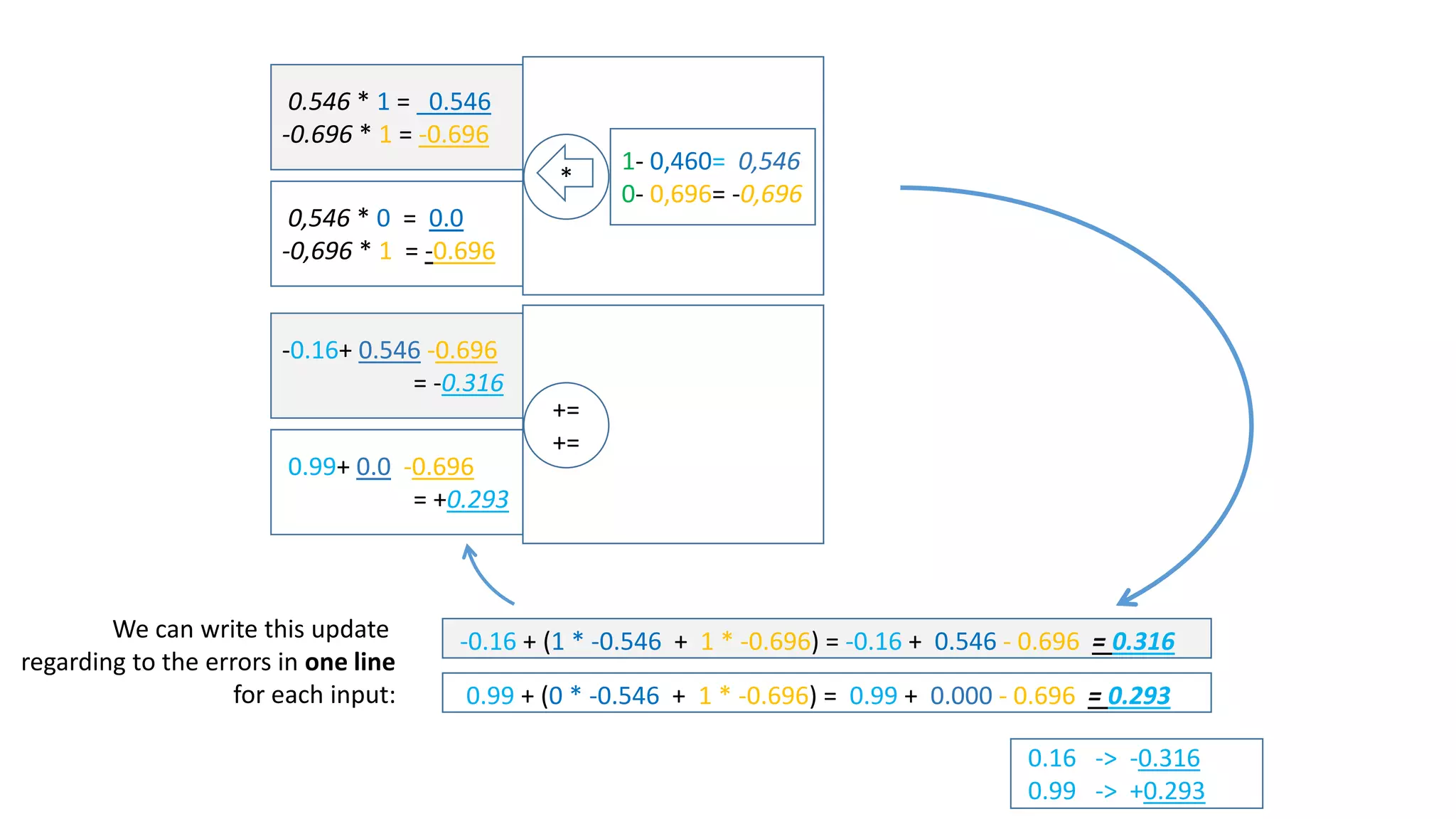
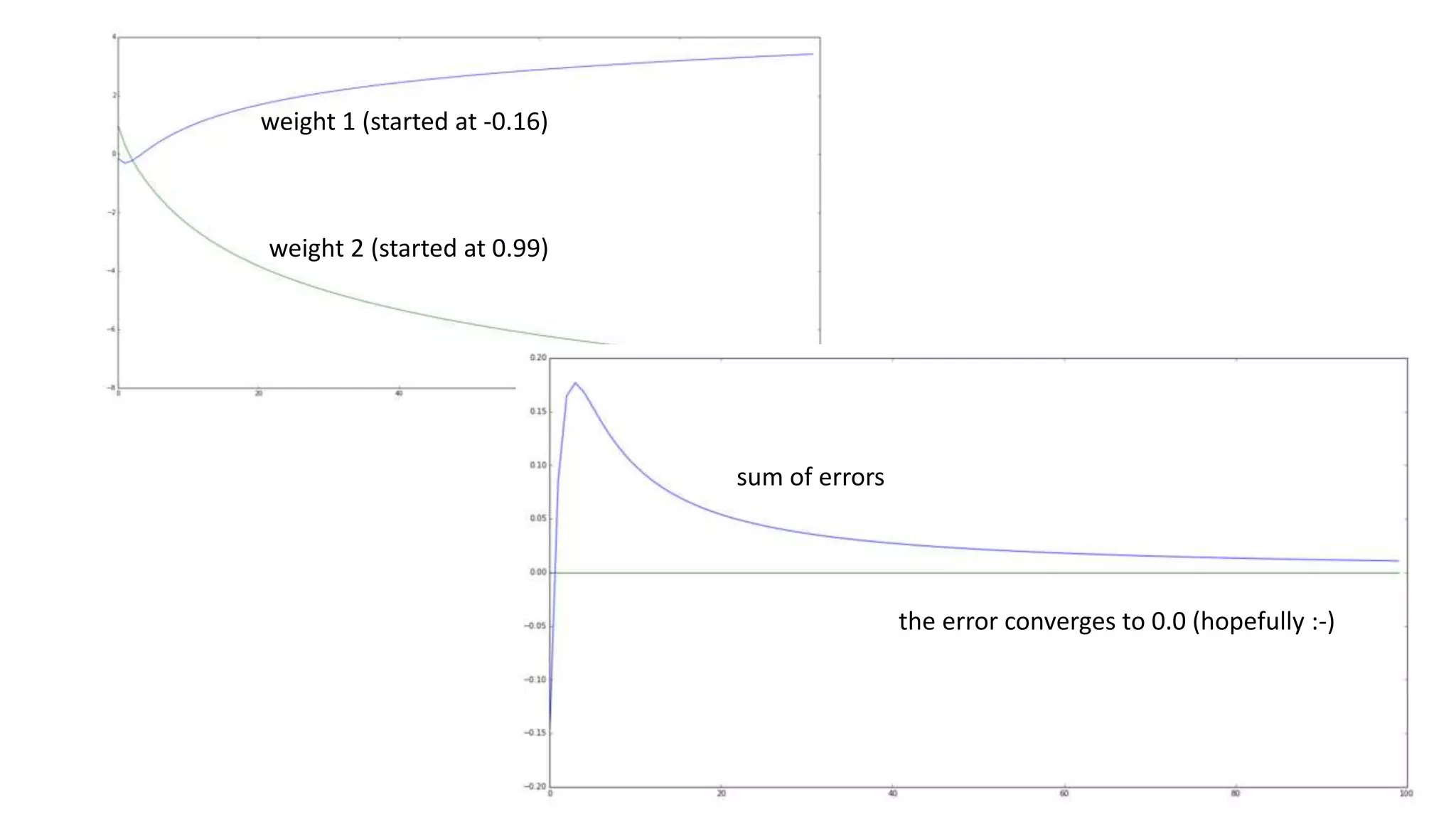
25. sum of error == 0!
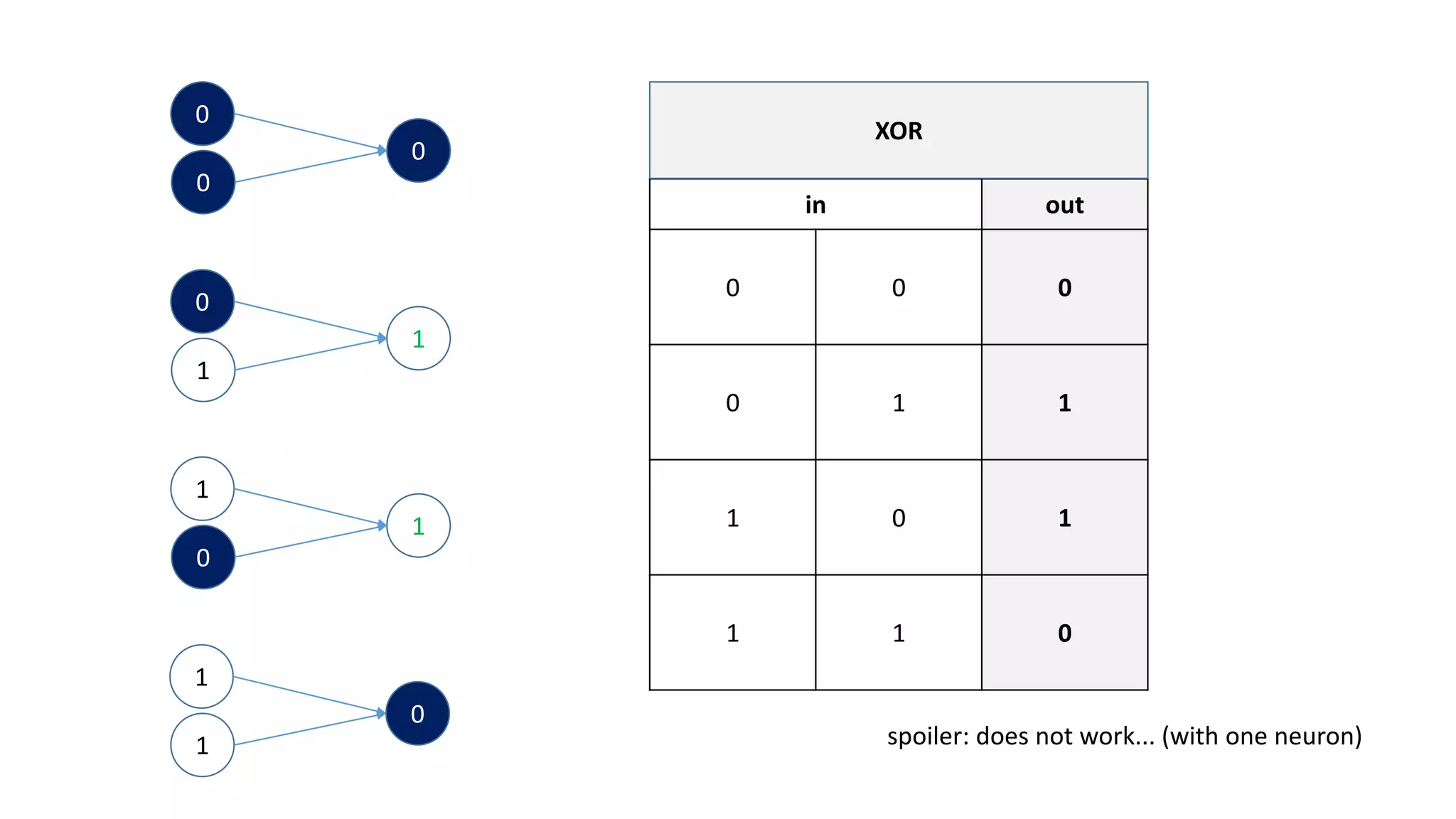
But…:
[0,0] -> out = 0.5 -> error = -0.5
[0,1] -> out = 0.5 -> error = 0.5
[1,0] -> out = 0.5 -> error = 0.5
[1,1] -> out = 0.5 -> error = -0.5
The weights are actually both 0!
If you think about it, it‘s pretty obvious.
Every weight has to be the same, because
a 1 or 0 leads to 0 or 1
in the same amount of cases
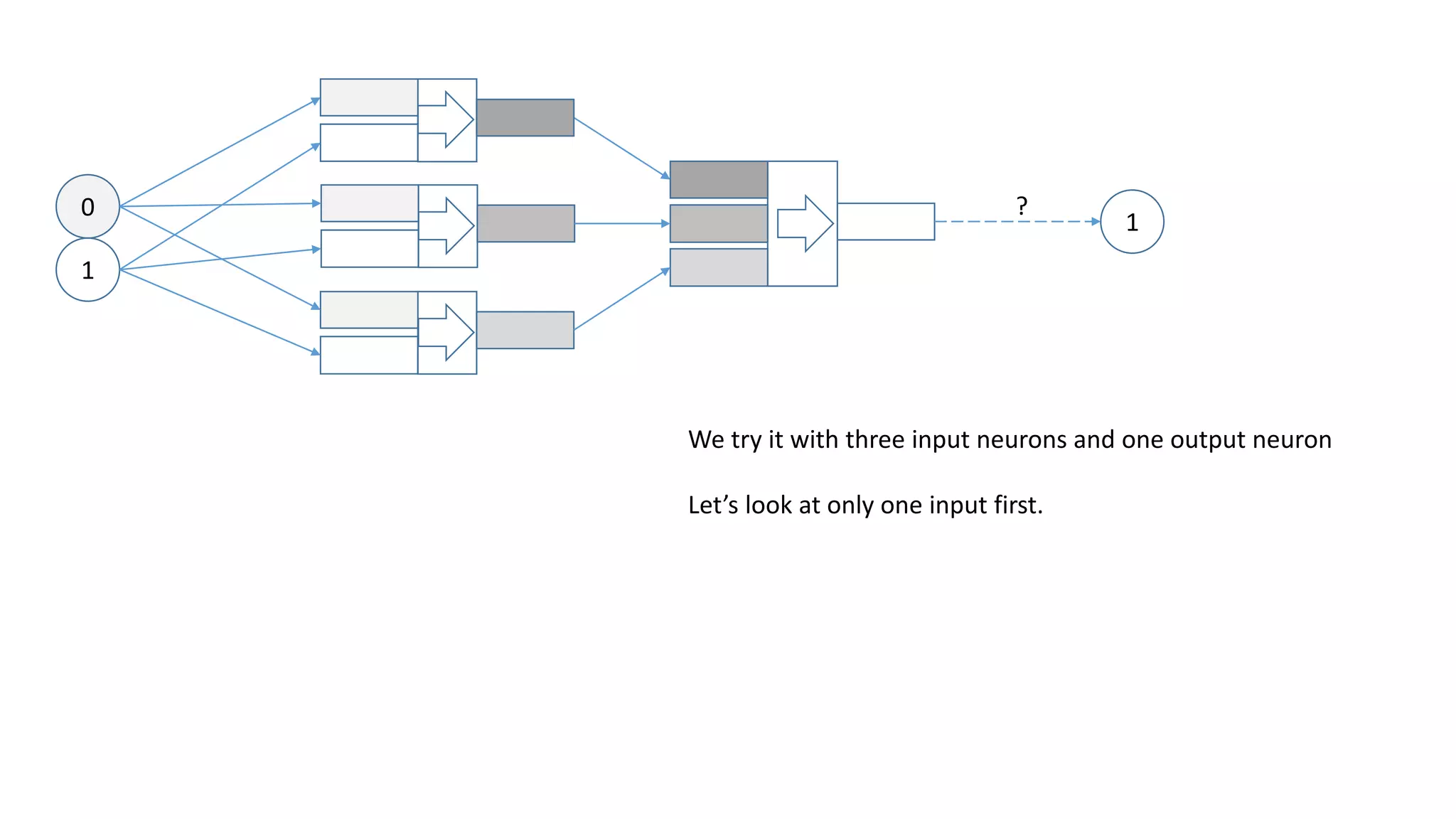
For XOR to work we need more layers!

26. 0
1
1
?
We try it with three input neurons and one output neuron
Let’s look at only one input first.

27. 0
1
0.81
-0.84
0.299
0.90
-0.63 0.588
-0.77
0.88
0.707
-0.79
0.69
0.667
0.80
sig( 0*0.81 + 1*-0.84 ) = sig(-0.84) = 0.299
sig( 0.299*0.90 + 0.707*-0.63 + 0.667*0,80) = sig(-0.353) = 0.588
The forward calculation for one input
The output is 1 that’s good! – let’s check the other inputs:
layer0 layer1
In layer2 we have not 0 or 1 as input, but fractions!
1
!

28. layer2layer0 layer1
0.81
-0.84
0.500
0.299
0.692
0.491
0.90
-0.63
0.630
0.588
0.662
0.619
-0.77
0.88
-0.79
0.69
0.80
0.500
0.707
0.315
0.527
0.500
0.667
0.310
0.474
first results for all inputs (not so good…)
The forward calculation for ALL FOUR inputs
1.0
1.0
1.0
1.0
For all 4 inputs the results are not so good…
we have to update the weights… layer by layer…

29. 0.81
-0.84
0.84
-0.69-0.77
0.88
-0.79
0.69
0.75
l2_error
0-r1= -0.630
1-r2= 0.411
1-r3= 0.337
0-r4= -0.619
l2_delta
sig‘(0.63)*-0.63=-0.146
sig‘(0.58)* 0.41= 0.099
sig‘(0.66)* 0.34= 0.075
sig‘(0.62)*-0.62=-0.14
0.90 + (0.500*-0.146 + 0.299*0.099 + 0.692*0.075 + 0.491*-0.14) = 0.84
-0.63 + (0.500*-0.146 + 0.707*0.099 + 0.315*0.075 + 0.527*-0.14) = -0.69
0.80 + (0.500*-0.146 + 0.667*0.099 + 0.310*0.075 + 0.474*-0.14) = 0.75
same as before (but with more values…)
0.500
0.299
0.692
0.491
0.500
0.707
0.315
0.527
0.500
0.667
0.310
0.474
* * * *
+=
+=
+=
+=
+=
+=
0,0 -> r1= 0.630
0,1 -> r2= 0.588
1,0 -> r3= 0.662
1,1 -> r4= 0.619
Backward Propagation:
Now we update the old weights
regarding to the errors of all inputs.
First in layer 2
0.90
-0.63
0.80

30. 0.795
-0.861
0.81 + (0*-0.033 + 0*0.018 + 1*0.014 + 1*-0.033) = 0.795
-0.84 + (0*-0.033 + 1*0.018 + 0*0.014 + 1*-0.033) = -0.861
Again as before (but with more values…)
0.500
0.299
0.692
0.491
* * *
+=
+=
+=
+=
0,0 -> r1= 0.5
0,1 -> r2= 0.299
1,0 -> r3= 0.692
1,1 -> r4= 0.491
l1_delta
sig‘(0.500) *-0.132 =-0.033
sig‘(0.299) * 0.090 = 0.018
sig‘(0.692) * 0.068 = 0.014
sig‘(0.491) *-0.131 =-0.033
l1_error =
l2_delta * weight of neuron 1 (to l2)
0,0 -> -0.146*0.90 = -0.132
0,1 -> 0.099*0.90 = 0.090
1,0 -> 0.075*0.90 = 0.068
1,1 -> 0.140*0.90 = -0.131
And now the weights in layer 1!
The error in neuron1
is a fraction of the error
in the output neuron (l2)
Therefore we take the delta-error of layer2;
neuron1 accounted 0.90 to this error:
l2_delta * weight of neuron 1 to l2
And of this we get the delta again -> l1_delta
*
+=
+=
0.81
-0.84
Neuron 1 in layer 1:

31. error curve (depends strongly on the start weights)
np.random.seed(11) np.random.seed(44) np.random.seed(101) np.random.seed(1023)
but in converges pretty good (mostly…)
Others:
(for python users: the starter weights have been generated with:
np.random.seed(245))

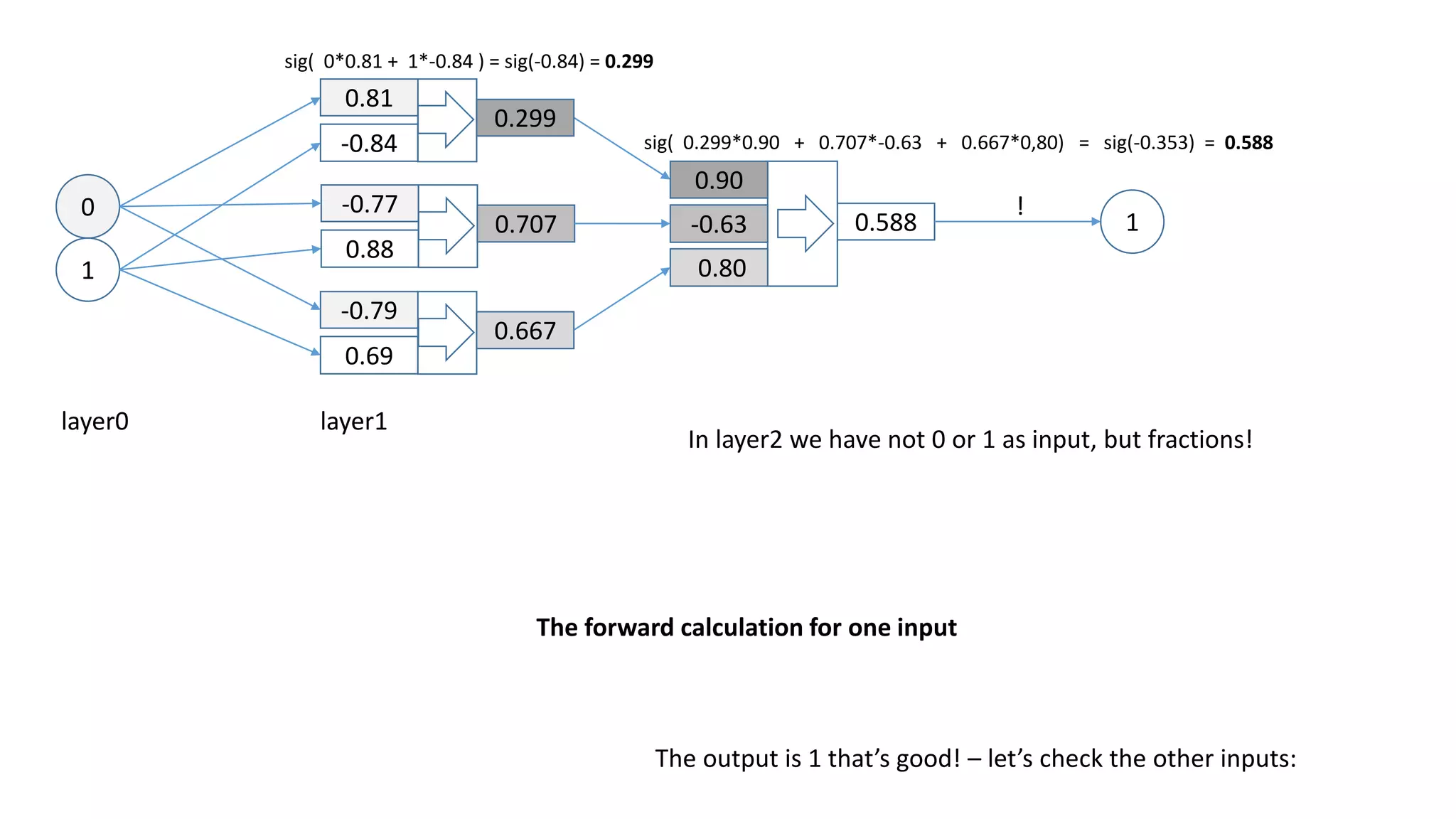
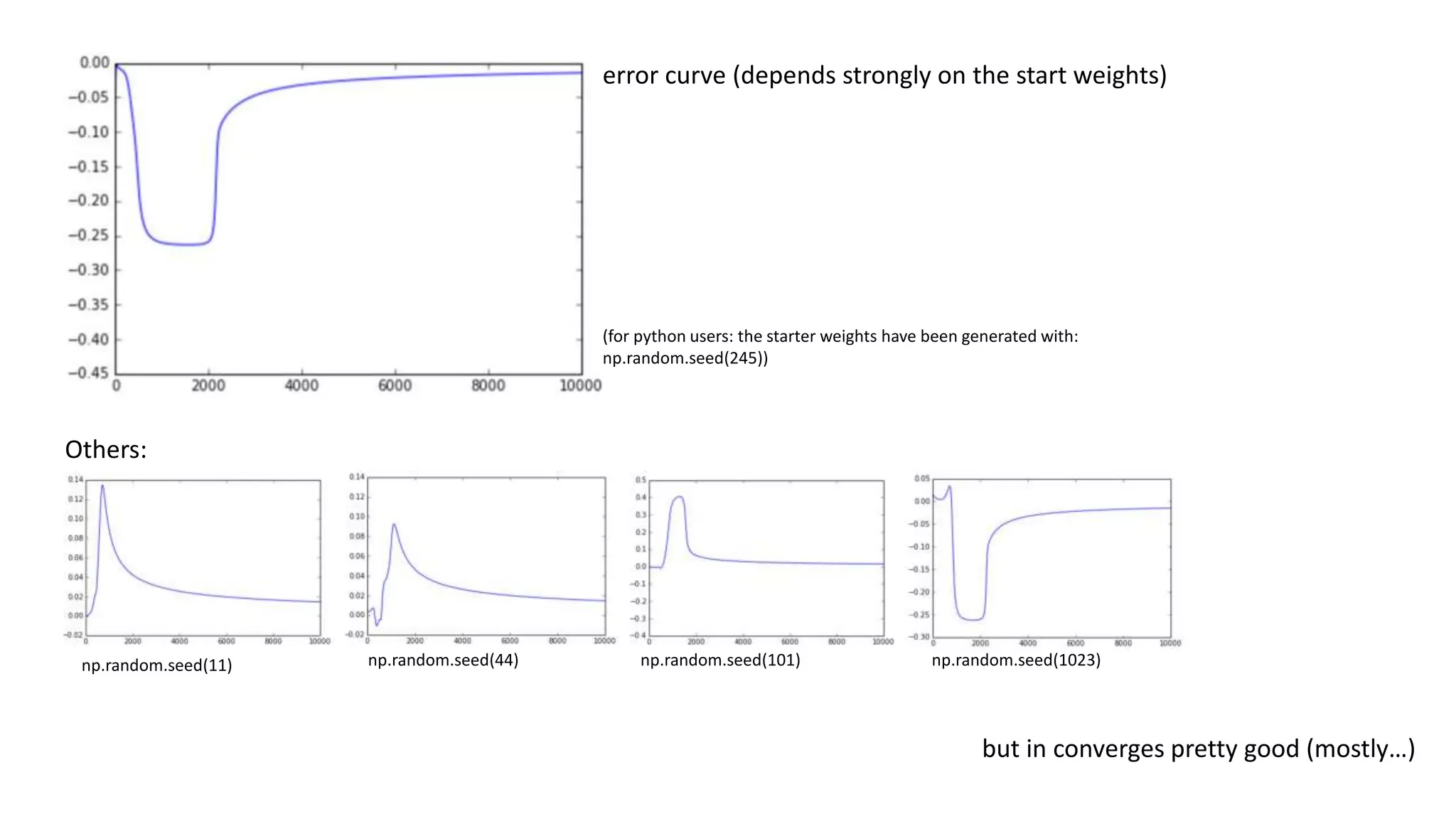
32. np.random.seed(25)
WOOPS!
Output:
0,0 -> [ 0.0214737 ]
0,1 -> [ 0.98097769]
1,0 -> [ 0.9810124 ]
1,1 -> [ 0.50051869] ? – probably runs into a local minimum…

33. That’s it so far – hope you had a good ride.
Obviously there are more questions coming up after this session, which I might dig into later:
• Why are there so different error curves?
• How to avoid a wrong output like the last error curve.
• How many iterations does a neural network has to do, to learn?
• How many neurons to take?
• How deep the layers should be (deep learning)?
• Are there other functions to use instead of the sigmoid function?
• Different nets working together
• etc etc…