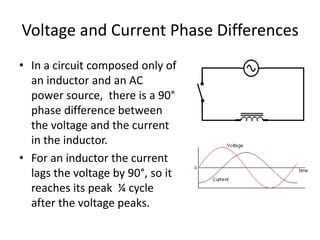
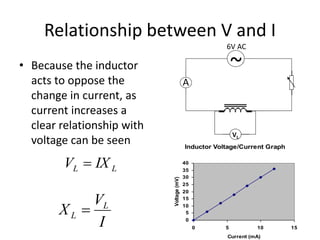
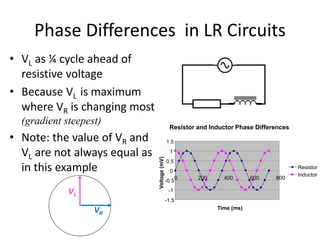
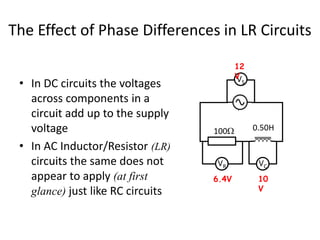
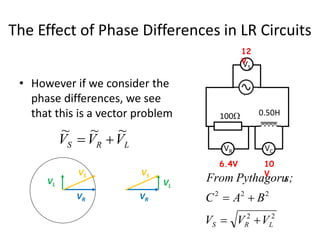
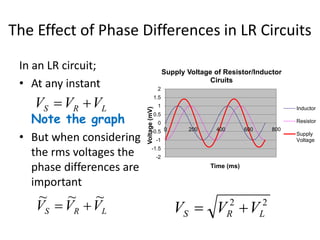
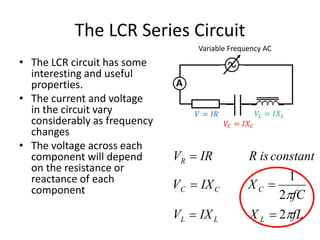
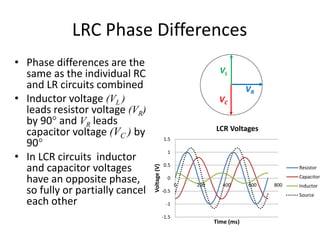
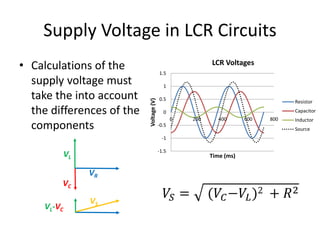
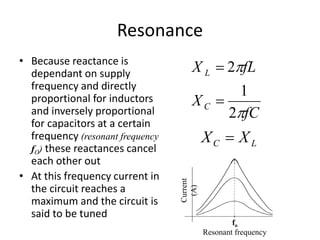
Inductors play an important role in AC circuits by opposing any changes in current through induction. The opposition is known as reactance. In an inductor, the current lags the voltage by 90 degrees. In an LCR series circuit, the voltages across each component depend on frequency and have different phase relationships. At resonance, the inductor and capacitor reactances cancel out, resulting in maximum current.

1. Inductors in AC
Circuits

2. Inductors
• An inductor affects a circuit
whenever current (I) is changing.
• The magnetic field generated by
the inductor acts to induce an
opposing current (Lenz’s Law).
• The ideal inductor stores energy in
its magnetic field which is then
returned to the circuit as electrical
energy, the only energy loss is from
the resistance of the circuit.

3. Inductors in AC
• In an AC circuit current is
constantly changing so
inductors play an
important role
• The current opposing
ability of inductors is called
reactance and given the
symbol XL
• Like XC the units are Ohms

4. Voltage and Current Phase Differences
• In a circuit composed only of
an inductor and an AC
power source, there is a 90°
phase difference between
the voltage and the current
in the inductor.
• For an inductor the current
lags the voltage by 90°, so it
reaches its peak ¼ cycle
after the voltage peaks.

5. Relationship between V and I
• Because the inductor
acts to oppose the
change in current, as
current increases a
clear relationship with
voltage can be seen
Inductor Voltage/Current Graph
40
35
30
25
20
15
10
5
0
0 5 10 15
Current (mA)
Voltage (mV)
L L V  IX
V
X L
I
L 
~
VL
A
6V AC

6. Examples
1. Find the inductor voltage of an AC circuit with a
reactance of 2.4 and a current of 0.18A
0.43V
2. An inductor has a voltage of 8.2V AC and a
reactance of 54. Calculate the current of the
circuit.
0.15A
3. Calculate the reactance of a circuit with an
inductor voltage of 16V and a current of 1.2A
13

8. Factors Affecting Reactance (XL )
• Increasing the size of the inductor (L) will induce a higher opposing
voltage and therefore increase XL
L X L 
• Increasing frequency increases induced current (increasing
reactance). This is because more frequent creation and collapse of
magnetic field produces greater opposing current
X f L 
• The reactance of a capacitor with a supply frequency f;
X fL X L L L  2 or 

9. Examples
1. A 0.5H inductor is connected to a 6V 50Hz AC
supply.
a) Calculate the reactance of the inductor
157
b) The RMS current in the circuit
0.038A
2. What size inductor is needed to give an
reactance of 25 in a 18V 60Hz circuit?
66 mF

11. • VL as ¼ cycle ahead of
resistive voltage
• Because VL is maximum
where VR is changing most
(gradient steepest)
• Note: the value of VR and
VL are not always equal as
in this example
Resistor and Inductor Phase Differences
1.5
1
0.5
0
-0.5
-1
-1.5
0 200 400 600 800
Time (ms)
Voltage (mV)
Resistor
Inductor
Phase Differences in LR Circuits
VL
VR

12. The Effect of Phase Differences in LR Circuits
• In DC circuits the voltages
across components in a
circuit add up to the supply
voltage
• In AC Inductor/Resistor (LR)
circuits the same does not
appear to apply (at first
glance) just like RC circuits
12
V
VS
100 0.50H
VR VC
6.4V 10
V

13. The Effect of Phase Differences in LR Circuits
• However if we consider the
phase differences, we see
that this is a vector problem
VL
~ ~ ~
V  V 
V
S R L VS
VR
12
V
100 0.50H
From
Pythagorus; VL
2 2 2
C  A 
B
2 2
V  V 
V
S R L VS
VR
VS
VR VC
6.4V 10
V

14. The Effect of Phase Differences in LR Circuits
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
Supply Voltage of Resistor/Inductor
Ciruits
0 200 400 600 800
Voltage (mV)
Time (ms)
Inductor
Resistor
Supply
Voltage
In an LR circuit;
• At any instant
S R L V V V
Note the graph
• But when considering
the rms voltages the
phase differences are
important
~ ~ ~
  2 2
S R L V V V
S R L V  V V

15. Exercises
1. Find the AC supply voltage of an LR circuit where the
resistor voltage is 3.4V and the inductor voltage is
1.5V
3.7V
2. Calculate the voltage across the resistor in an AC
circuit with a supply voltage of 8.5V and a inductor
voltage of 2.4V
8.2V
3. Calculate the voltage across the inductor in an 12V AC
circuit with a voltage of 8.5V across the resistor.
8.5V
4. Find the supply voltage of an 60Hz AC circuit with a
120V across a 2k resistor and an inductor voltage of
0.80V
120V

17. Impedance
• As with LR circuits impedance relates supply
voltage to current.
V IZ

so;
V
S
I
S
and
Z

• Using Pythagoras from the addition of phasors
2 2
L Z  R  X

18. Examples
1. Calculate the impedance of an LR circuit with a
resistance of 75 and a reactance of 15 
76 
2. An LR circuit has an impedance of 65  and has
a resistance of 24 . What is the reactance of
the circuit?
60 
3. Find the resistance of an LR circuit with 25 
impedance and 12  reactance.
22 

20. Inductors in DC c.f. AC
18V DC 18V AC 50Hz
A A
400mH 400mH
0.15A
• Both circuits have the same components but behave
quite differently because of their power supplies;
1. Find the resistance of the resistor
2. What assumption did you make in 1?
3. Calculate the reactance of the circuit
4. What is the impedance of the circuit?
5. Calculate the current in the AC circuit

21. The LCR Series Circuit
• The LCR circuit has some
interesting and useful
properties.
• The current and voltage
in the circuit vary
considerably as frequency
changes
• The voltage across each
component will depend
on the resistance or
reactance of each
component
Variable Frequency AC
A
R is constant
1
fC
V IR
V IX
X

 
C C
C
R
2

2
V IX fL
L L

 
L
X
푉 = 퐼푅
푉퐶 = 퐼푋퐶
푉퐿 = 퐼푋퐿

22. LRC Phase Differences
• Phase differences are the
same as the individual RC
and LR circuits combined
• Inductor voltage (VL )
leads resistor voltage (VR)
by 90 and VR leads
capacitor voltage (VC ) by
90
• In LCR circuits inductor
and capacitor voltages
have an opposite phase,
so fully or partially cancel
each other
VL
VR
VC
1.5
1
0.5
0
-0.5
-1
-1.5
LCR Voltages
0 200 400 600 800
Voltage (V)
Time (ms)
Resistor
Capacitor
Inductor
Source

23. LCR Phasors
• In most cases the L, C and R
phasors will be different lengths
• Most commonly voltage and
reactance/resistor phasors are
considered
• In either case remember to
calculate the differences between
the two opposite phasors before
calculating VS or Z
VL
VR
VC
VL-VC
VS
VR
XL
R
XC
XL-XC
Z
R
LorC effective L C V V V
T C L X  X  X
or;

24. Supply Voltage in LCR Circuits
• Calculations of the
supply voltage must
take the into account
the differences of the
components
VL
VR
VC
VL-VC
VS
1.5
1
0.5
0
-0.5
-1
-1.5
LCR Voltages
0 200 400 600 800
푉푆 = (푉퐶−푉퐿)2 + 푅2
Voltage (V)
Time (ms)
Resistor
Capacitor
Inductor
Source

25. Examples
1. Calculate the supply voltage of an LCR circuit
where the capacitor voltage is 12V, the resistor
voltage is 18V  and the inductor voltage is 6V
19V
2. Calculate the resistor voltage of an LCR circuit
where the supply voltage 240V, the capacitor
voltage is 85V and the inductor voltage is 220V
198 
3. Find the inductor voltage of an LCR circuit where
the supply voltage is 12V, the resistor voltage is
9.8V and the capacitor voltage is 4.5V
2.4V

27. Impedance in LCR Circuits
Z
2 2 Z X X R C L  (  ) 
• Impedance is a measure
of the combined
opposition to alternating
current of the
components of a circuit.
• It describes not only the
relative amplitudes of the
voltage and current, but
also the relative phases
the components in the
circuit.
• Impedance has the
symbol Z and units Ohms
XL
R
XC
XL-XC
R

28. Examples
1. Calculate the impedance of an LCR circuit where
the capacitor reactance is 25, the resistance is
50  and the inductor reactance is 15 
51 
2. Calculate the resistance of an LCR circuit where
the impedance 110  is capacitor reactance is
64  and the inductor reactance is 25 
100 
3. Find the inductor reactance of an LCR circuit
where the impedance is 120 , the resistance is
110  and the capacitor reactance is 30 
120 

30. Resonance
• Because reactance is
dependant on supply
frequency and directly
proportional for inductors
and inversely proportional
for capacitors at a certain
frequency (resonant frequency
fO) these reactances cancel
each other out
• At this frequency current in
the circuit reaches a
maximum and the circuit is
said to be tuned
fL

1
fC
2

2


L
C
X
X
C L X  X
fo
Resonant frequency
Current
(A)

31. Resonant Frequency
• Because at resonance;
so;
f C
C L X  X
f L
o
o


2
1
2 
LC
fo
2
1

Note that the resonant frequency is
independent of the resistance

32. Examples
1. Calculate the resonance frequency of an LRC
circuit with a 200F capacitor and a 0.5H
inductor.
2. Find the size of the capacitor needed for
resonance in an LRC with a resonant
frequency of 50Hz and an inductor of 0.20H

33. Voltage at Resonance
• At resonance;
• And because Z = R
X 
X
L C
V
V
L C
I
so

;
V V
I

L C
V V IR S R  
And cancel each
other out

34. Examples

35. Exercises
ESA Pg 282
Activity 16E, 16F, 16G, 16H
ABA
Pg 186-196