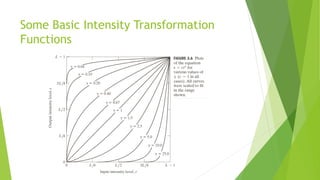
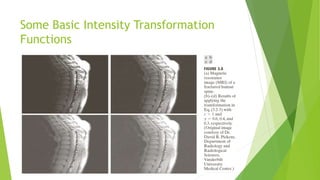
Digital Image Processing: Image Enhancement in Spatial Domain This document discusses image enhancement techniques in the spatial domain. It describes how spatial domain methods directly manipulate pixel values, considering their spatial relationships within the image. These include single-pixel operations like intensity transformations, neighborhood operations like averaging filters, and geometric spatial transformations like scaling and rotation. Specific techniques are explained, such as logarithmic transforms to expand dark pixel values, power law transforms for gamma correction, and averaging neighborhoods to improve signal-to-noise ratio. Examples of code are provided to implement these spatial domain image enhancement methods.

1. Digital Image Processing:
Image Enhancement in Spatial
Domain
Nidhi Sharma

2. Image Enhancement
 Image enhancement in the spatial domain is a technique used to improve the
visual quality of digital images by directly manipulating the pixel values.
 It involves modifying the image pixel by pixel, considering their spatial
relationships within the image.
 Image enhancement approaches fall into two broad categories:
 Spatial domain methods
 Point processes
 Area processes
 Frame process
 Frequency domain methods

3. Image Enhancement: Spatial Domain
 The term spatial domain refers to the aggregate of pixels composing an
image.
 Spatial domain methods are procedures that operate directly on these pixels.
Spatial domain processes will be denoted by the expression
g (x, y) = T [f (x, y)]
where f(x, y) is the input image, g(x, y) is the processed image, and T is an
operator on f, defined over some neighborhood of (x, y).
For example:
T can operate on a set of input images, such as performing the pixel-by-pixel sum
of K images for noise reduction.

4. Spatial Image Enhancement
 Single-pixel operation (Intensity Transformation)
Negative Image, contrast stretching etc.
 Neighbourhood operations
Averaging filter, median filtering etc.
 Geometric spatial transformations
Scaling, Rotation, Translations et

5. Single Pixel Operations

6. Neighbourhood Operations

7. Geometric Spatial Operators

8. Averaging
 Often done to improve SNR.
avgI = (img1+img2+img3+img4+img5)/5;
Remember that the data is Uint8 type…..which may saturate the sum values to 255!
So
avgI = (im2double(img1)+im2double(img2)+ im2double(img3)+ im2double(img4)+
im2double(img5))/5;
Im2double also rescales range to [0,1]

9. Resizing and Transforming
 Use ‘montage’ to see and compare image side by side
Montage ({image1, image2})
avgGray = im2gray (avgI);
avgIreduced = imresize( avgI, 0.75);
avgIsquared = imresize( avgI, 2000, 2000);
avgIrotated = imrotate( avgI, 30, ‘crop’);

10.  Imwrite( avgI, “filename.png”); % to save image as a given file name
 Imwrite( avgI, “filename.jpg”, “Quality”, 80); % to save image as a given file name

11. Some Basic Intensity Transformation
Functions
 Image Negatives
s = L – 1 – r
S is the output intensity value
L is the highest intensity levels
r is the input intensity value
 Particularly suited for enhancing white or gray detail embedded in dark
regions of an image, especially when the black areas are dominant in size

12. Some Basic Intensity Transformation
Functions
 Log Transformations
 s = c log(1 + r) where , c is a constant
 It maps a narrow range of low intensity values in the input into a wide range of output
levels
 The opposite is true of higher values of input levels
 It expands the values of dark pixels in an image while compressing the higher level
values
 It compresses the dynamic range of images with large variations in pixel values

13. % Read the input image
inputImage = imread('input_image.jpg'); % Replace 'input_image.jpg' with your image file name and
extension
% Convert the input image to double precision for accurate calculations
inputImage = im2double(inputImage);
% Perform log transformation
c = 1; % Constant value for scaling
outputImage = c * log(1 + inputImage);
% Rescale the output image to the range [0, 1] for display
outputImage = (outputImage - min(outputImage(:))) / (max(outputImage(:)) - min(outputImage(:)));
% Display the input and output images figure;
subplot(1, 2, 1);
imshow(inputImage);
title('Input Image');
subplot(1, 2, 2);
imshow(outputImage);
title('Log Transformed Image');
% Save the output image
imwrite(outputImage, 'output_image.jpg'); % Replace 'output_image.jpg' with your desired output image
file name and extension

14. Example:

15. Some Basic Intensity Transformation
Functions
 Power Law (Gamma) Transformations
 s = c rγ
 c and γ are both positive constants
 With fractional values(0<γ<1) of gamma map a narrow range of dark input
values into a wider range of output values, with the opposite being true for
higher values (γ >1)of input levels.
 C=gamma=1 means it is an identity transformations.
 Variety of devices used for image capture , printing, and display respond
according to a power law.
 Process used to correct these power law response phenomena is called
gamma correction.

16. Some Basic Intensity Transformation
Functions

17. Some Basic Intensity Transformation
Functions

18. Power Law (Gamma) Transformations
 Images that are not corrected properly look either bleached out or too dark.
 Varying gamma changes not only intensity, but also the ratio of red to green to blue in
a color images.
 Gamma correction has become increasingly important, as the use of the digital images
over internet.
 Useful for general purpose contrast manipulation.
 Apply gamma correction on CRT (Television, monitor), printers, scanners etc.
 Gamma value depends on device.

19. Some Basic Intensity Transformation
Functions