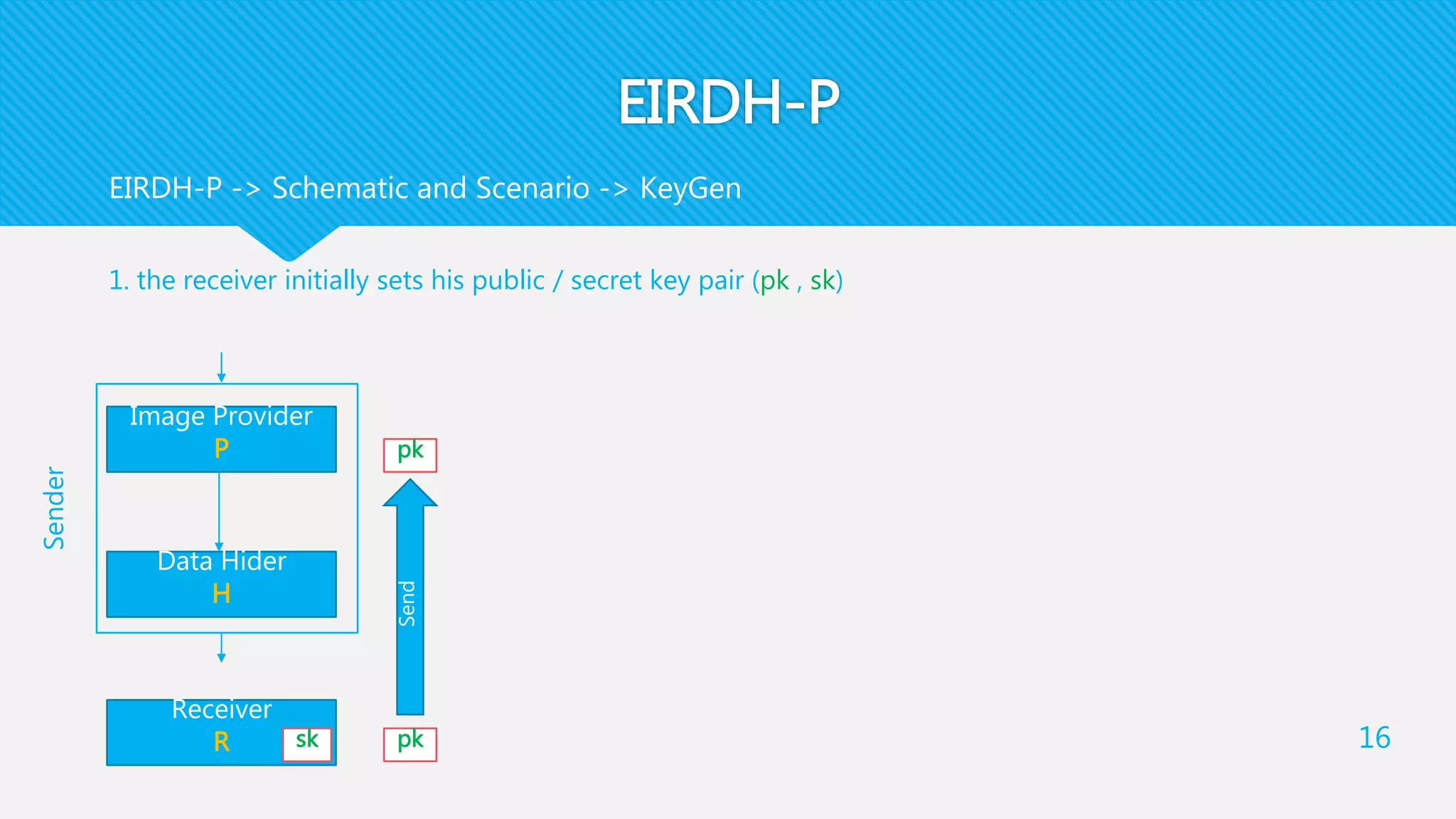
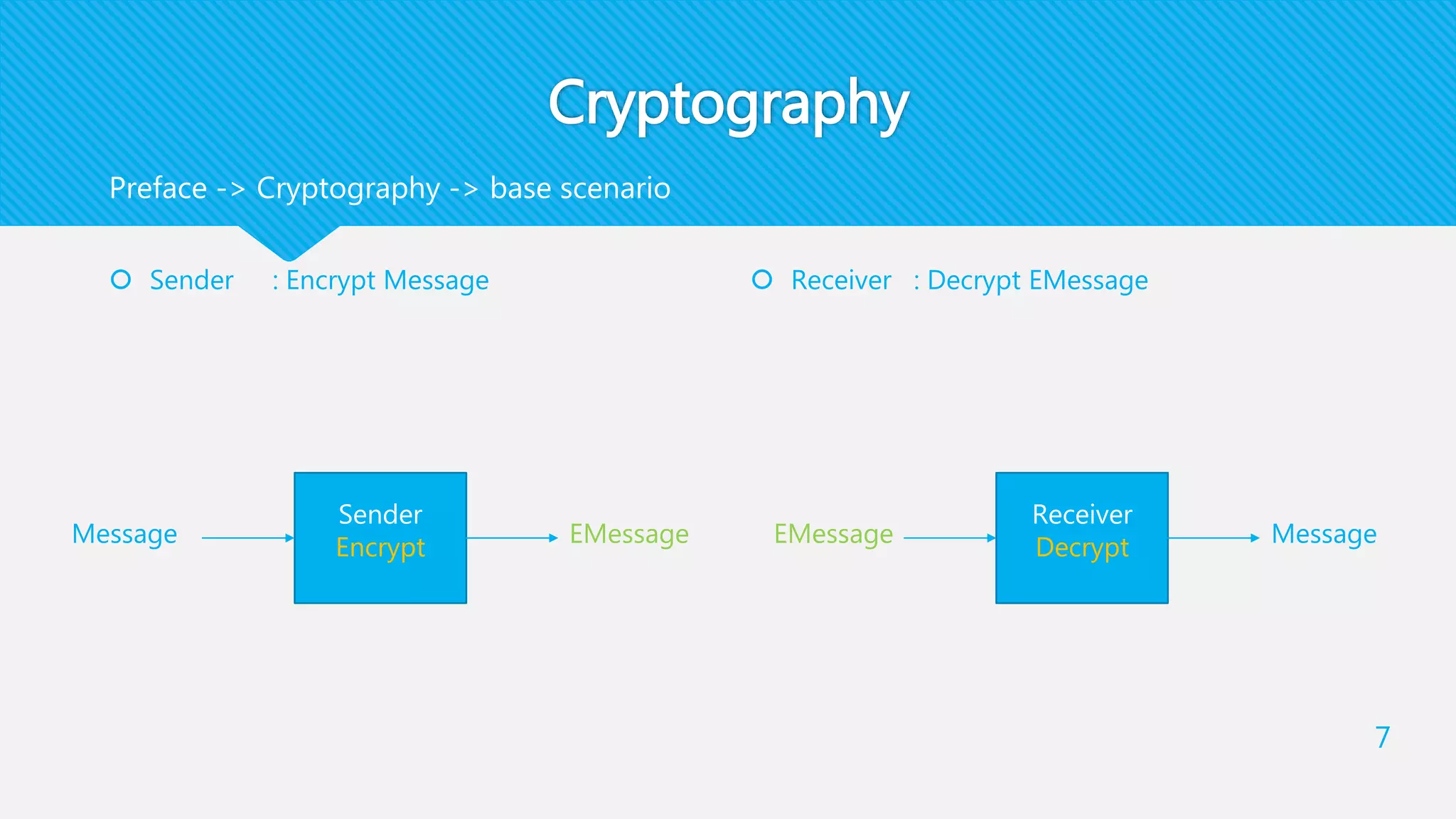
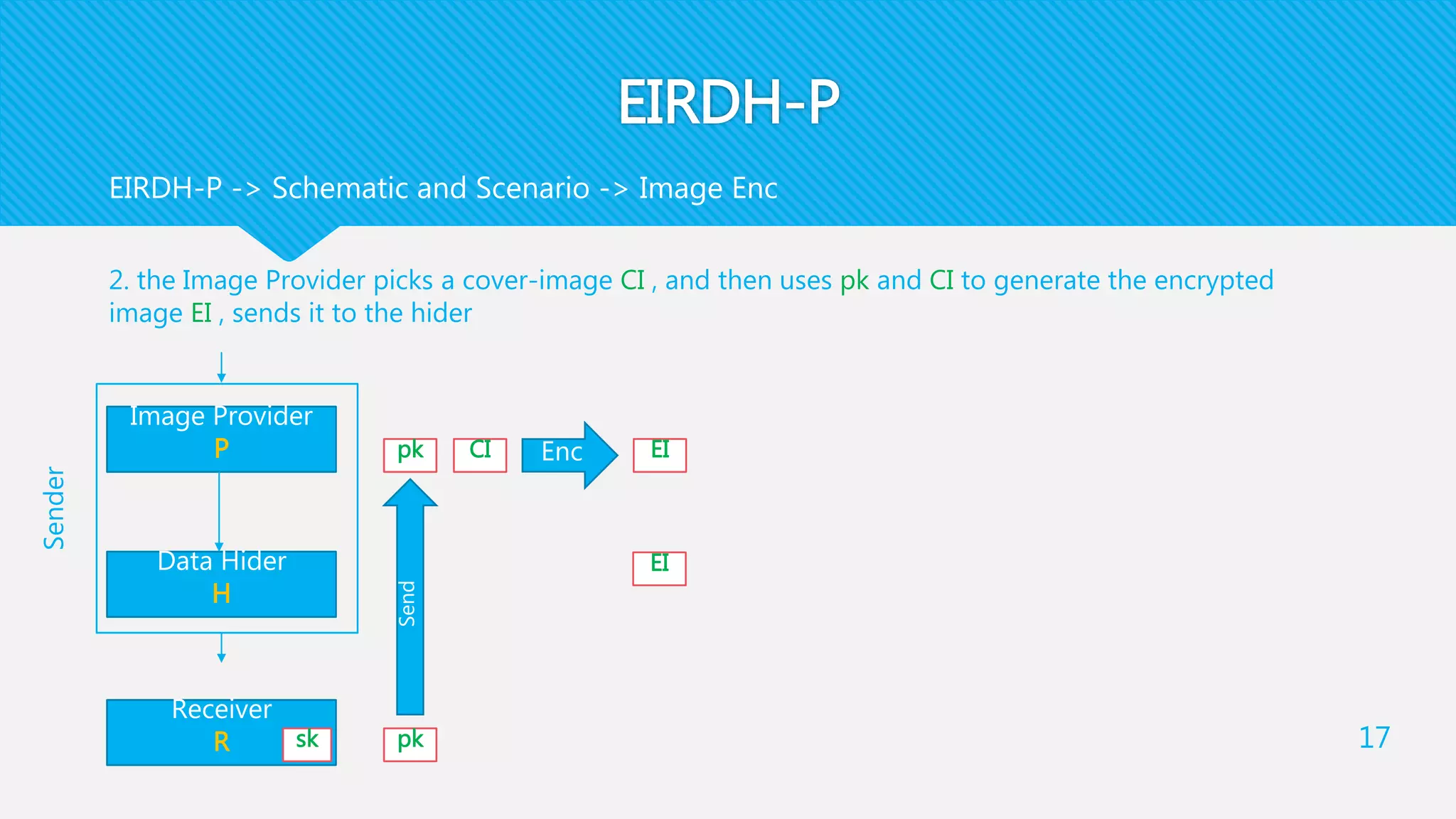
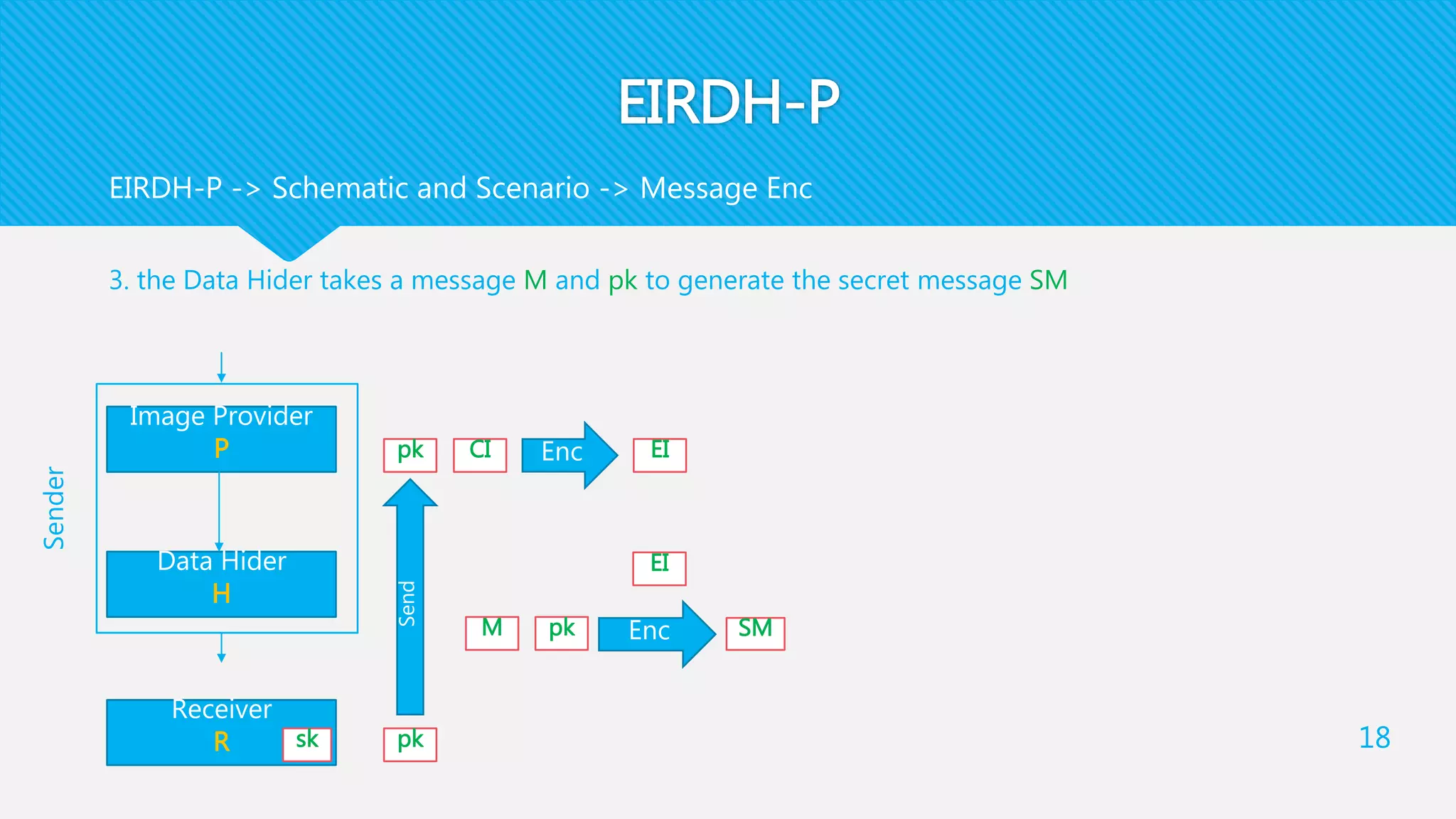
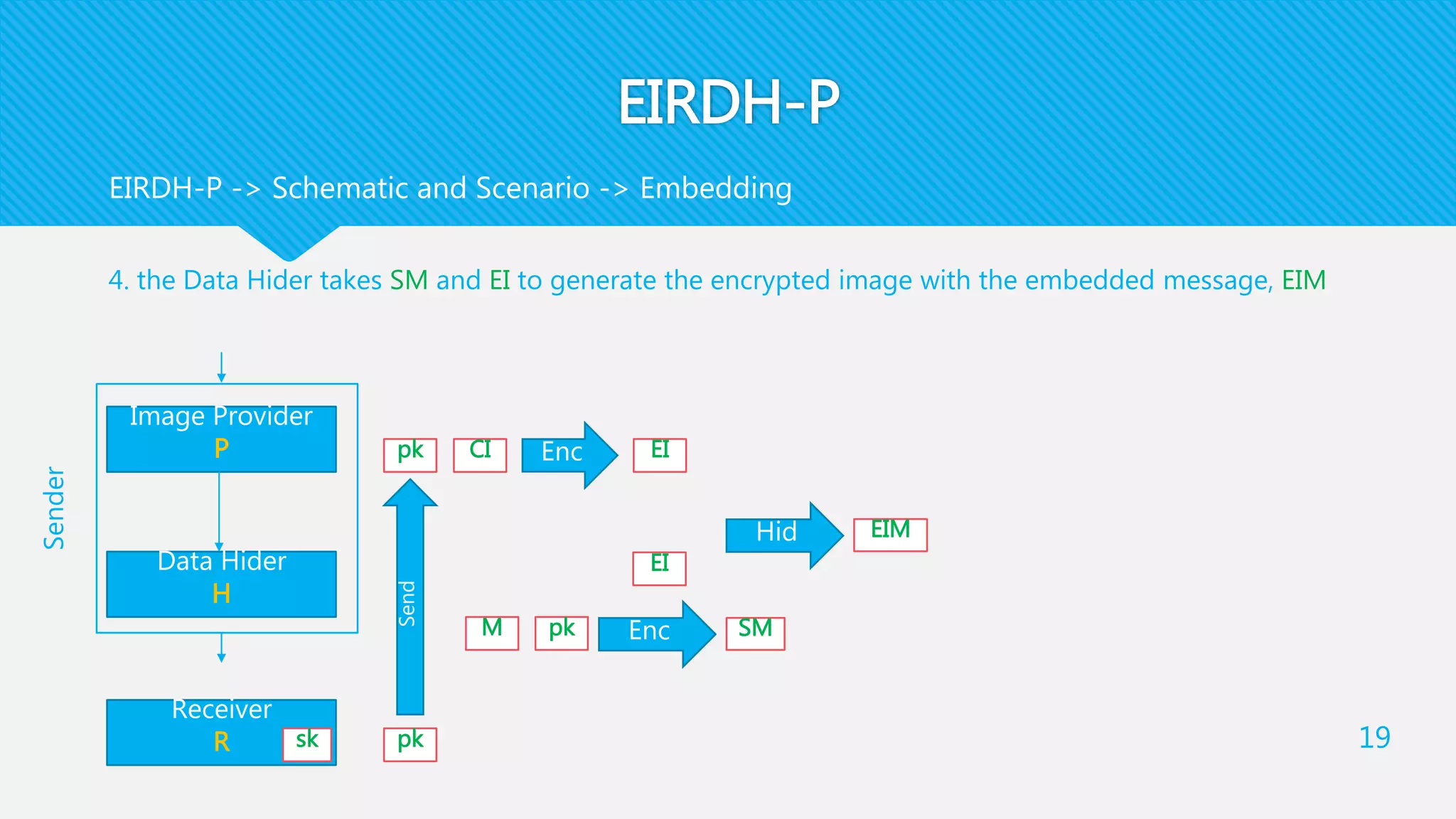
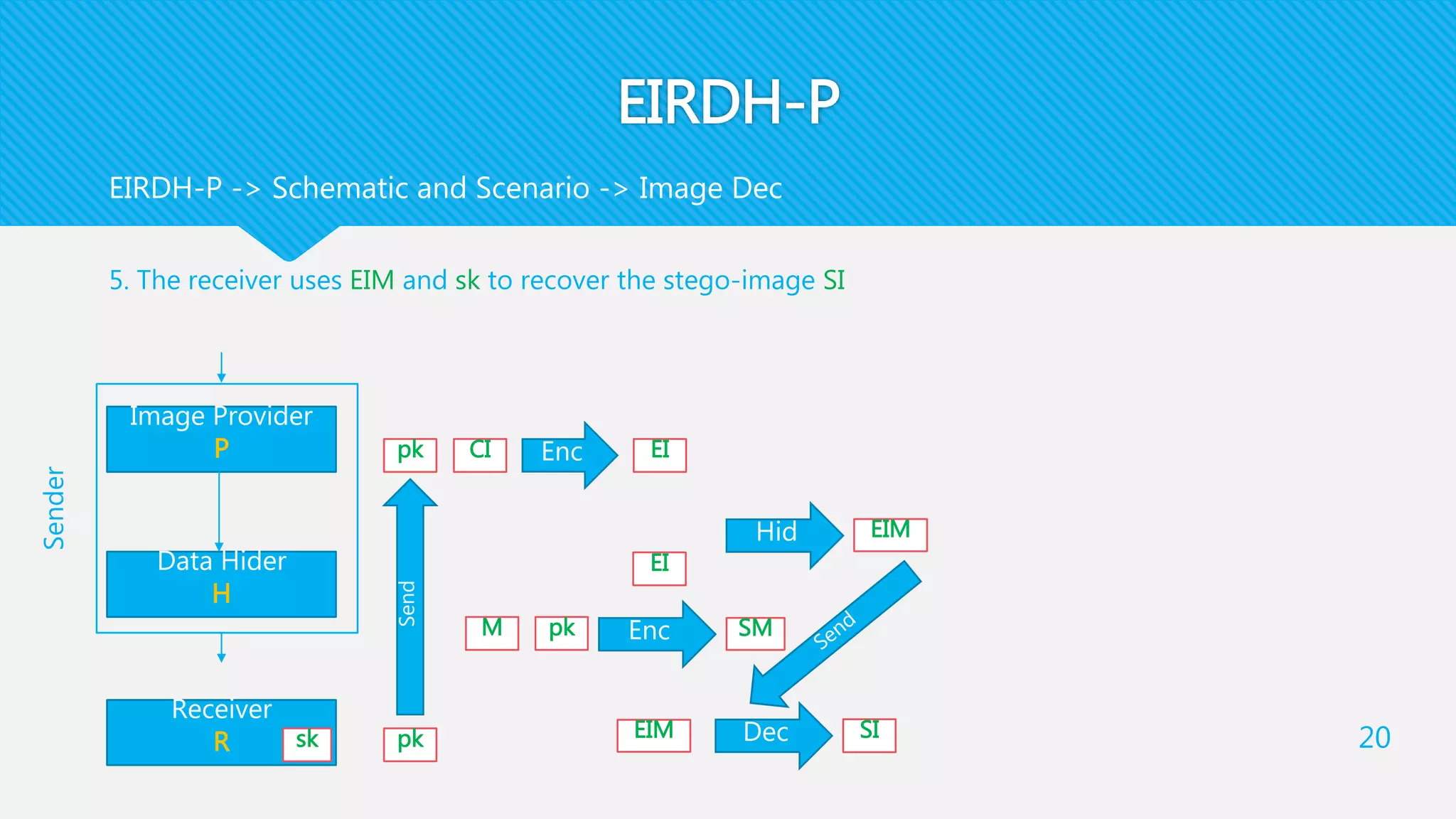
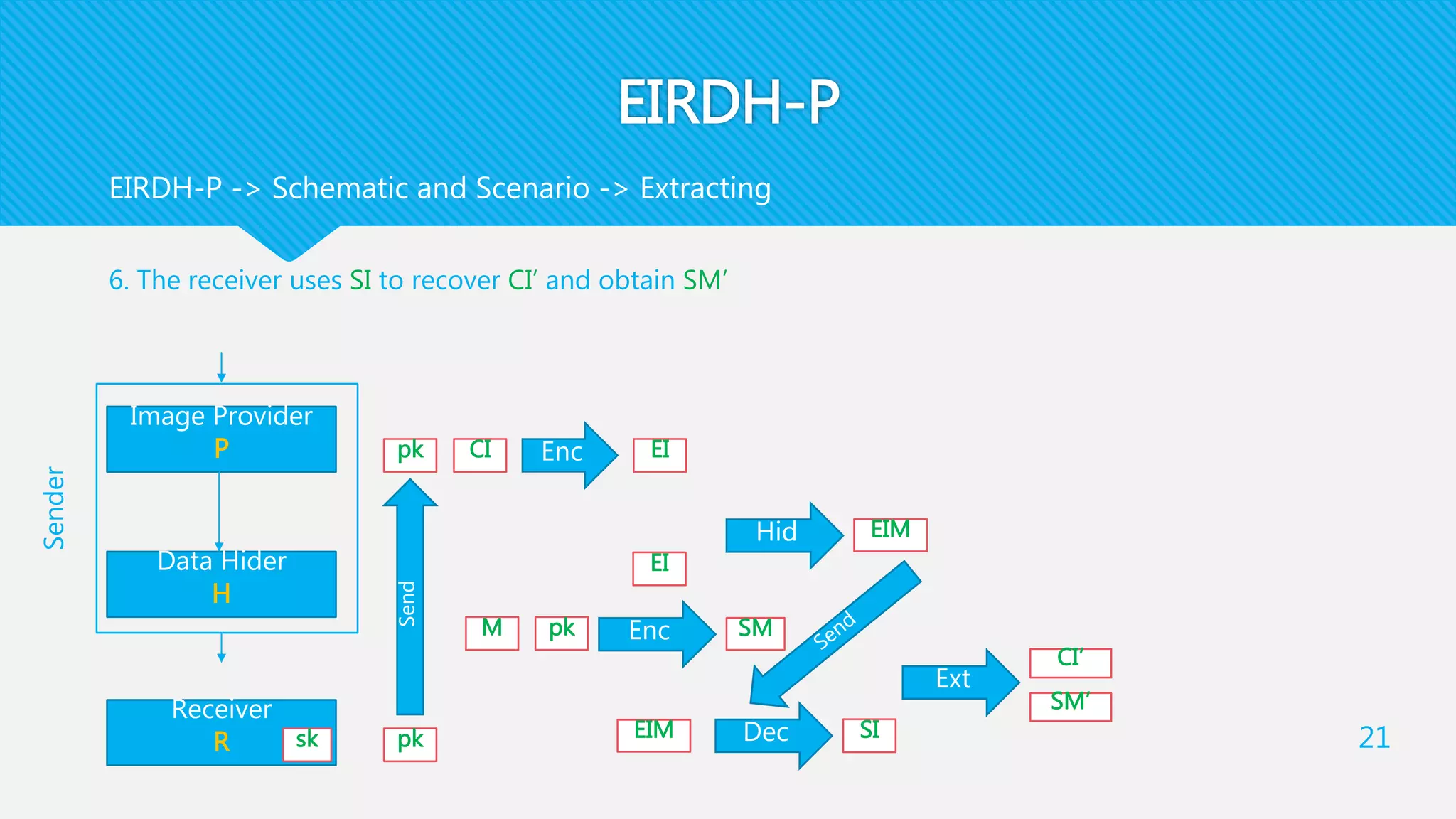
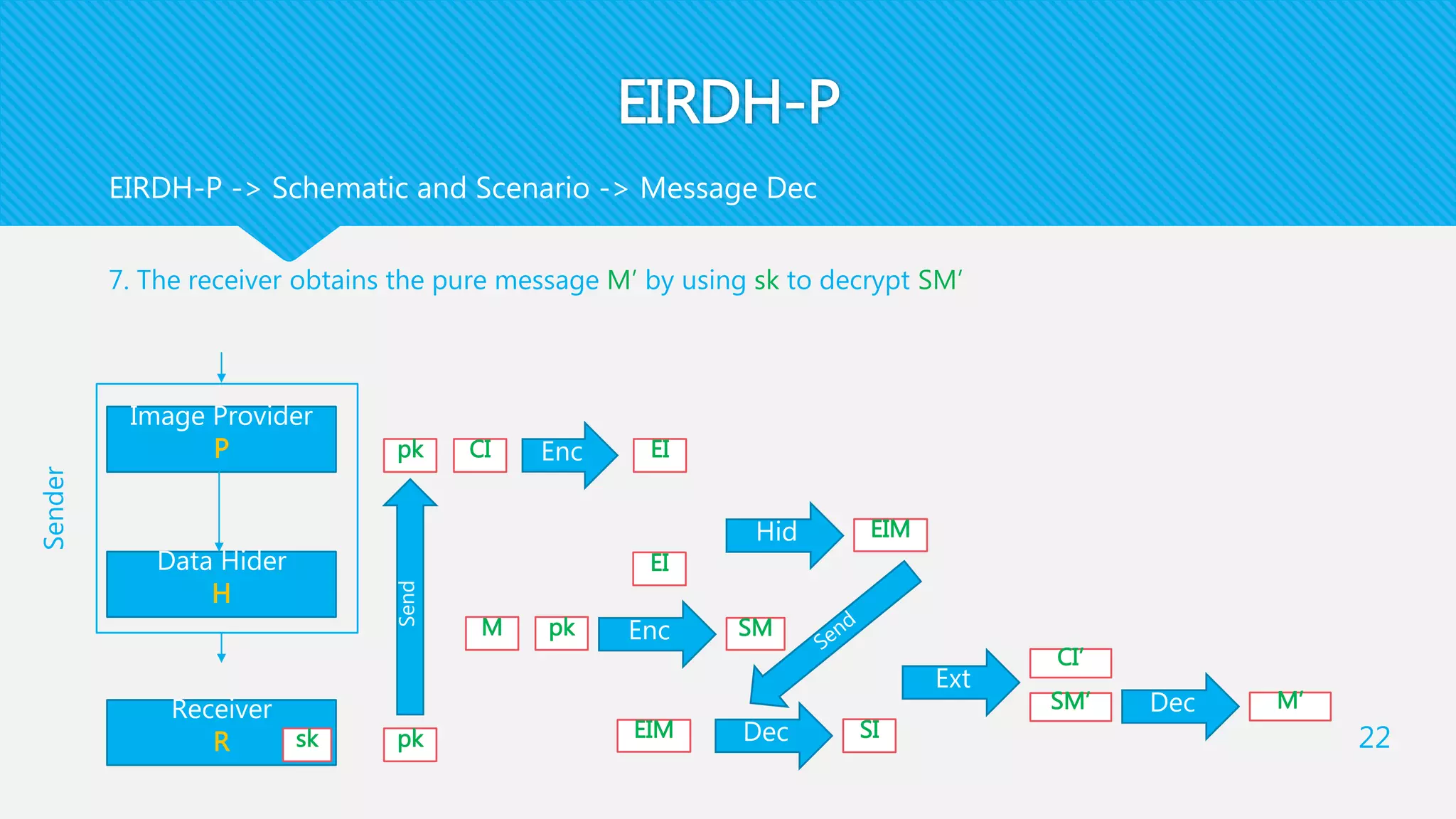
1) EIRDH-P combines public key cryptography and steganography by encrypting images and embedding secret messages within the encrypted images. 2) It involves an Image Provider who encrypts a cover image using public key encryption. A Data Hider then embeds a secret message within the encrypted image. 3) The receiver decrypts the stego-image to extract the secret message and recover the original cover image using their private key.

1. Image
Cryptography &
Steganography
Master :
Dr. Ghaderi
Mohammad Amin Amjadi
Winter 2015

2. Main Paper
Encrypted image-based reversible data hiding
with public key cryptography from difference
expansion
Chih-Wei Shiu , Yu-Chi Chen , Wien Hong
2015 Elsevier B.V. All rights reserved
2

3. Content
a) Preface
b) EIRDH-P
c) new EIRDH-P
3

4. Image
Preface -> Image
4
Image : a Matrix of Pixels

5. Pixel
Preface -> Image -> Pixel
5
+
+
=
Red
Property
(8 bit)
24 bit Image
Green
Property
(8 bit)
Blue
Property
(8 bit)
BGR
LSBMSBLSBMSBLSBMSB
000000000000000000000000
Pixel : 24 bit
LSB : Least significant bit
MSB : Most significant bit
RGB Mode

6. Cryptography
Goal : Security
Terms :
1) Cryptography
2) Encrypt
3) Decrypt
4) Public key Cryptography
6

7. Cryptography
 Sender : Encrypt Message  Receiver : Decrypt EMessage
7
Preface -> Cryptography -> base scenario
Sender
EncryptMessage EMessage
Receiver
DecryptEMessage Message

8. Cryptography
1. Change Location (reordering) 2. Mapping
8
Preface -> Cryptography -> base Algorithms
21
43
34
12
21
43
F(2)F(1)
F(4)F(3)

9. Cryptography
1. Symmetric-Key Cryptography
sender and receiver using same key
key is secret
2. Public-Key Cryptography
anyone can access to the public key
only receiver has the Private Key
9
Preface -> Cryptography -> Category

10. Steganography
Goal : Hide Message/Data
Terms :
1) DH : Data Hiding
2) RDH : Reversible Data Hiding
10

11. Steganography
 use Cover Image / Hide Message / Extract Message
 Sender : Hide Message inside Cover Image
 Receiver : Extract secret Message
11
Preface -> Steganography -> base scenario
Sender
Cover Image
Cover Image(Message)
Message
ReceiverCover Image(Message)
Cover Image
Message

12. Steganography
 LSB
Image quality of Cover Image
12
Preface -> Steganography -> base Algorithms
BGR
LSBMSBLSBMSBLSBMSB
000000000000000000000000
BGR
LSBMSBLSBMSBLSBMSB
000000000000000000000000
3bit of Data in any pixel of Cover Image 8bit of Data in any pixel of Cover Image

13. Cryptography & Steganography
13
Preface -> compare Cryptography and Steganography
Encryption
Decryption

14. Cryptography & Steganography
14
Preface -> compare Cryptography and Steganography
Cover Image (512 x 512)
94 KB
LSB Algorithm
Using Jpeg Format
Message (450 x 321)
20 KB
Stego (512 x 512)
37.6 KB

15. EIRDH-P
Combine Cryptography & Steganography
Terms :
1) EIRDH : encrypted image-based
reversible data hiding
2) EIRDH-P : encrypted image-
based reversible data hiding
(EIRDH) with public key
cryptography
3) Image Provider
4) Hider
15

16. EIRDH-P
1. the receiver initially sets his public / secret key pair (pk , sk)
16
EIRDH-P -> Schematic and Scenario -> KeyGen
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
Send

17. EIRDH-P
2. the Image Provider picks a cover-image CI , and then uses pk and CI to generate the encrypted
image EI , sends it to the hider
17
EIRDH-P -> Schematic and Scenario -> Image Enc
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EIEnc
Send
EI

18. EIRDH-P
3. the Data Hider takes a message M and pk to generate the secret message SM
18
EIRDH-P -> Schematic and Scenario -> Message Enc
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EI
EI
Enc
Send
M pk Enc SM

19. EIRDH-P
4. the Data Hider takes SM and EI to generate the encrypted image with the embedded message, EIM
19
EIRDH-P -> Schematic and Scenario -> Embedding
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EIEnc
Send
EI
M pk Enc SM
Hid EIM

20. EIRDH-P
5. The receiver uses EIM and sk to recover the stego-image SI
20
EIRDH-P -> Schematic and Scenario -> Image Dec
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EIEnc
Send
EI
M pk Enc SM
Hid EIM
EIM Dec SI

21. EIRDH-P
6. The receiver uses SI to recover CI’ and obtain SM’
21
EIRDH-P -> Schematic and Scenario -> Extracting
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EIEnc
Send
EI
M pk Enc SM
Hid EIM
EIM Dec SI
Ext
SM’
CI’

22. EIRDH-P
7. The receiver obtains the pure message M’ by using sk to decrypt SM’
22
EIRDH-P -> Schematic and Scenario -> Message Dec
Receiver
R
Data Hider
H
Image Provider
P
sk pk
pk
Sender
CI EIEnc
Send
EI
M pk Enc SM
Hid EIM
EIM Dec SI
Ext
SM’
CI’
Dec M’

23. EIRDH-P
23
EIRDH-P -> Encryption Algorithm
Public
key
Diffie-
Hellman
RSAPaillier
 Terms :
1) gcd : Greatest common divisor
2) lcm : Least common multiple

24. EIRDH-P
1. Choose two distinct prime numbers p and q
p != q
p , q : Big
24
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53

25. EIRDH-P
2. Compute n = pq
25
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233

26. EIRDH-P
3. Compute φ(n) = φ(p)φ(q) = (p − 1)(q − 1) = n - (p + q -1) , where φ is Euler's totient function
26
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120

27. EIRDH-P
4. Choose an integer e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1
e is a prim Number on {1 to φ(n) }
𝑒 ∈ 𝑍 𝑛
∗
27
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17

28. EIRDH-P
5. Determine d as d ≡ e−1 (mod φ(n))
d⋅e ≡ 1 (mod φ(n))
d.e = 1 + k.φ(n)
28
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17
5. d = 2753 17 x 2753 mod 3120 = 1

29. EIRDH-P
6. public key : ( n , e )
29
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17
5. d = 2753 17 x 2753 mod 3120 = 1
6. public key : ( n , e ) = ( 3233 , 17 )

30. EIRDH-P
7. private key
a) ( n , d )
b) ( p , q ) , d mod (q-1) , d mod (p-1) , q-1 mod (p)
30
EIRDH-P -> Encryption Algorithm -> RSA -> KeyGen
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17
5. d = 2753 17 x 2753 mod 3120 = 1
6. public key : ( n , e ) = ( 3233 , 17 )
7. private key : ( n , d ) = ( 3233 , 2753 )

31. EIRDH-P
8. Encryption
m (Message) such that 0 ≤ m < n and gcd(m, n) = 1
c : ciphertext
𝑐 𝑚 = 𝑚 𝑒 𝑚𝑜𝑑 𝑛
31
EIRDH-P -> Encryption Algorithm -> RSA -> Encryption
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17
5. d = 2753 17 x 2753 mod 3120 = 1
6. public key : ( n , e ) = ( 3233 , 17 )
7. private key : ( n , d ) = ( 3233 , 2753 )
8. c(m) = 𝑚17
𝑚𝑜𝑑 3233

32. EIRDH-P
9. Decryption
𝑚 𝑐 = 𝑐 𝑑
𝑚𝑜𝑑 𝑛
32
EIRDH-P -> Encryption Algorithm -> RSA -> Decryption
1. p = 61 , q = 53
2. n = 61 x 53 = 3233
3. φ(n) = (61 − 1)(53 − 1) = 3120
4. e = 17
5. d = 2753 17 x 2753 mod 3120 = 1
6. public key : ( n , e ) = ( 3233 , 17 )
7. private key : ( n , d ) = ( 3233 , 2753 )
8. c(m) = 𝑚17
𝑚𝑜𝑑 3233
9. m(c) = 𝑐2753
𝑚𝑜𝑑 3233

33. EIRDH-P
1. Choose two large prime numbers p and q randomly
2. Compute n = pq , 𝜆 = 𝑙𝑐𝑚( 𝑝 − 1 , 𝑞 − 1 )
3. Select random integer g where 𝑔 ∈ 𝑍 𝑛2
∗
4. gcd 𝐿 𝑔 𝜆 𝑚𝑜𝑑 𝑁2 , 𝑁 = 1 ; where 𝐿 𝑥 =
𝑥
𝑁
5. ( N , g ) is public key
6. ( p , q , 𝜆 ) is private key
7. 𝑐 𝑚 = 𝑔 𝑚
𝑟 𝜆
𝑚𝑜𝑑𝑁2
where r is random such that 𝑟 ∈ 𝑍 𝑁
∗
8. 𝑚 𝑐 =
𝐿 𝑐 𝜆 𝑚𝑜𝑑 𝑁2
𝐿 𝑔 𝜆 𝑚𝑜𝑑 𝑁2 𝑚𝑜𝑑 𝑁
33
EIRDH-P -> Encryption Algorithm -> Paillier

34. new EIRDH-P
 each pixel is divided into two parts : an even integer and a bit, where the summation of them is
equal to the pixel value
any pixel = x + y + bit
(x , y) is an even integer , x > y
 [[m]] = c(m) = ciphertext of m
 [[m1]] [[m2]] = [[ m1 + m2 ]]
34
new EIRDH-P

35. new EIRDH-P
1. Receiver sets the public/secret key pair (pk, sk) as Paillier encryption
35
new EIRDH-P -> Algorithm -> KeyGen

36. new EIRDH-P
2. Image Provider pre-processes (x,y) to compute 𝑙 =
𝑥+𝑦
2
and 𝑑 = 𝑥 − 𝑦 , and then computes
𝑥′
= 𝑙 + 𝑑 and 𝑦′
= 𝑙 − 𝑑
Note that d can be positive or negative
He generates [ 𝑥′
] and [ 𝑦′
] by using pk to encrypt 𝑥′
, 𝑦′
Here [ 𝑥′
] and [ 𝑦′
] are the encrypted pixel pair in the encrypted image
This step will produce EI
36
new EIRDH-P -> Algorithm -> Image Enc
yx
Cover Image
Pre Process y'x' Encrypt [[y‘]][[x‘]]
Enc Image
𝑥′ = 𝑙 + 𝑑
𝑦′
= 𝑙 − 𝑑

37. new EIRDH-P
3. Data Hider generates the secret message SM by using pk to encrypt the message M
37
new EIRDH-P -> Algorithm -> Message Enc
EncM
pk
SM

38. new EIRDH-P
4. For a bit b of SM , Data Hider generates [𝑏] and computes 𝑥′′
= 𝑏 [ 𝑥′ ] and 𝑦′′
= [ 𝑦′
]
Note that [𝑏] is only inserted into the first encrypted pixel
Finally, he generates 𝑥′′
and 𝑦′′
as a pixel pair of EIM. This step will output EIM
38
new EIRDH-P -> Algorithm -> Embedding
[[y‘]][[x‘]][[y”]][[x”]] Embed
b = 1 , 𝑥′′
= [ 𝑥′ ] 1 , 𝑦′′
= 𝑦′
b = 0 , 𝑥′′
= [ 𝑥′ ] , 𝑦′′
= 𝑦′

39. new EIRDH-P
5. Receiver uses 𝑥 ′′
and 𝑦 ′′
and sk to recover x ″ , y ″ as a pixel pair of the stego-image SI
This step will finally output SI
39
new EIRDH-P -> Algorithm -> Image Dec
[[y”]][[x"]] Dec y “x “
Stego Image

40. new EIRDH-P
6. If x “ and y “ are both odd or both even , Receiver extracts b = 0 and recover x’ = x” and y’ = y”
if not, extracts b = 1 and recovers x’ = x”-1 and y’ = y” since b is only embedded into the first pixel
Receiver can easily compute 𝑙 =
𝑥′+𝑦′
2
and 𝑑 =
𝑥′− 𝑦′
2
and obtain the original pixel pair of CI by computing x
= 𝑙 +
𝑑+1
2
and y = 𝑙 −
𝑑
2
At the end, this step will output SM and recovers CI
40
new EIRDH-P -> Algorithm -> Extracting
y”x” Extract y‘x‘
Stego Image

41. new EIRDH-P
7. Receiver obtains the pure message M by using sk to decrypt SM
41
new EIRDH-P -> Algorithm -> Message Dec
y‘x‘ Recover yx
Stego Image

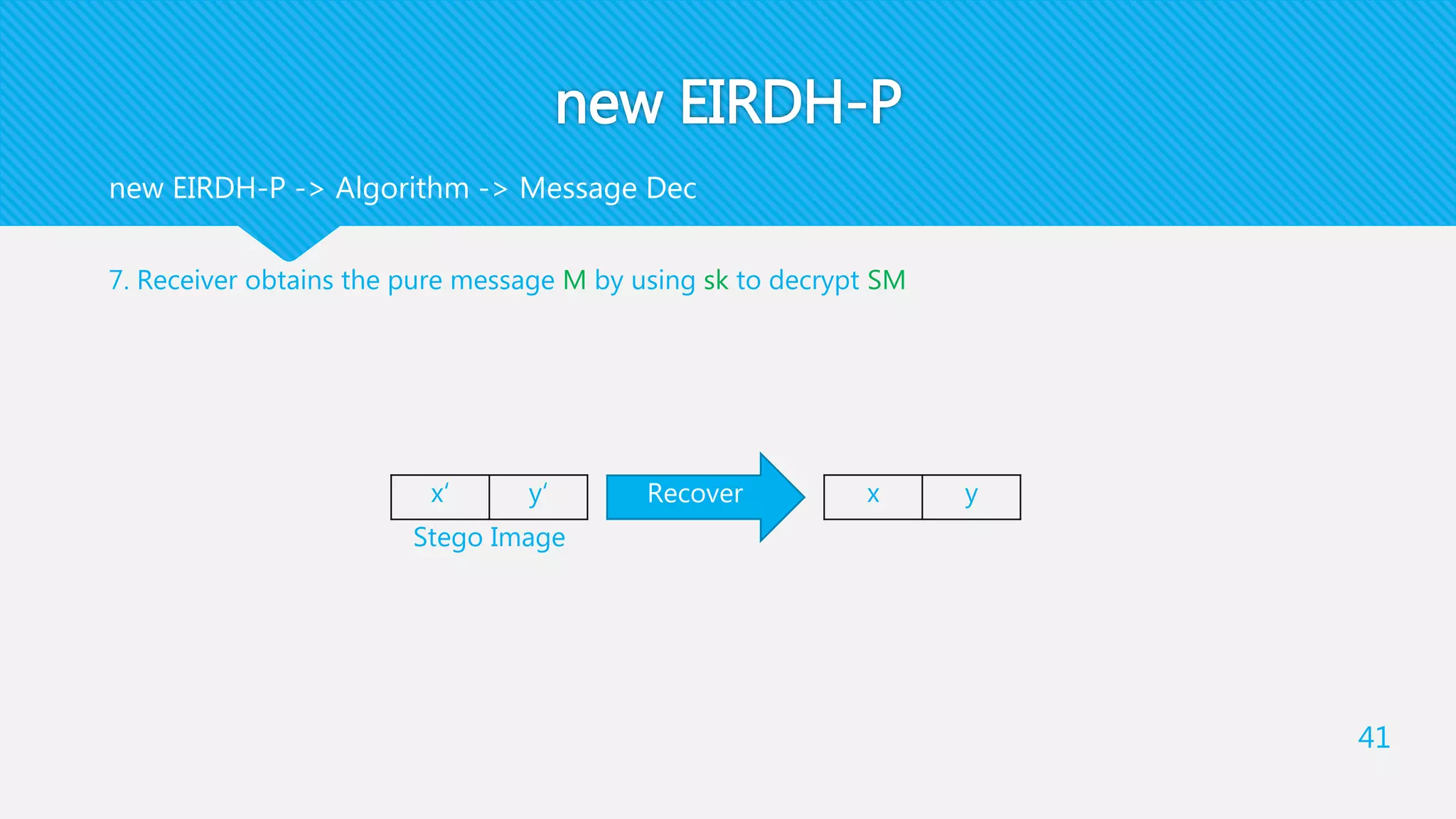
42. new EIRDH-P
42
new EIRDH-P -> Schematic
Cover Image
Pre Process Encrypt
Enc Image
𝑥′
= 𝑙 + 𝑑
𝑦′
= 𝑙 − 𝑑
[[y‘]][[x‘]][[y”]][[x”]] Embed
If bit = 1 , 𝑥′′
= [ 𝑥′ ] 1 , 𝑦′′
= 𝑦′
If bit = 0 , 𝑥′′
= [ 𝑥′ ] , 𝑦′′
= 𝑦′
[[y”]][[x"]]
Dec
y “x “
Stego Image
Extract y‘x‘ Recover
𝑙 =
𝑥′+𝑦′
2
, 𝑑 =
𝑥′− 𝑦′
2
x = 𝑙 +
𝑑+1
2
, y = 𝑙 −
𝑑
2
P
H
R

43. Question ?
43

44. Thanks
44