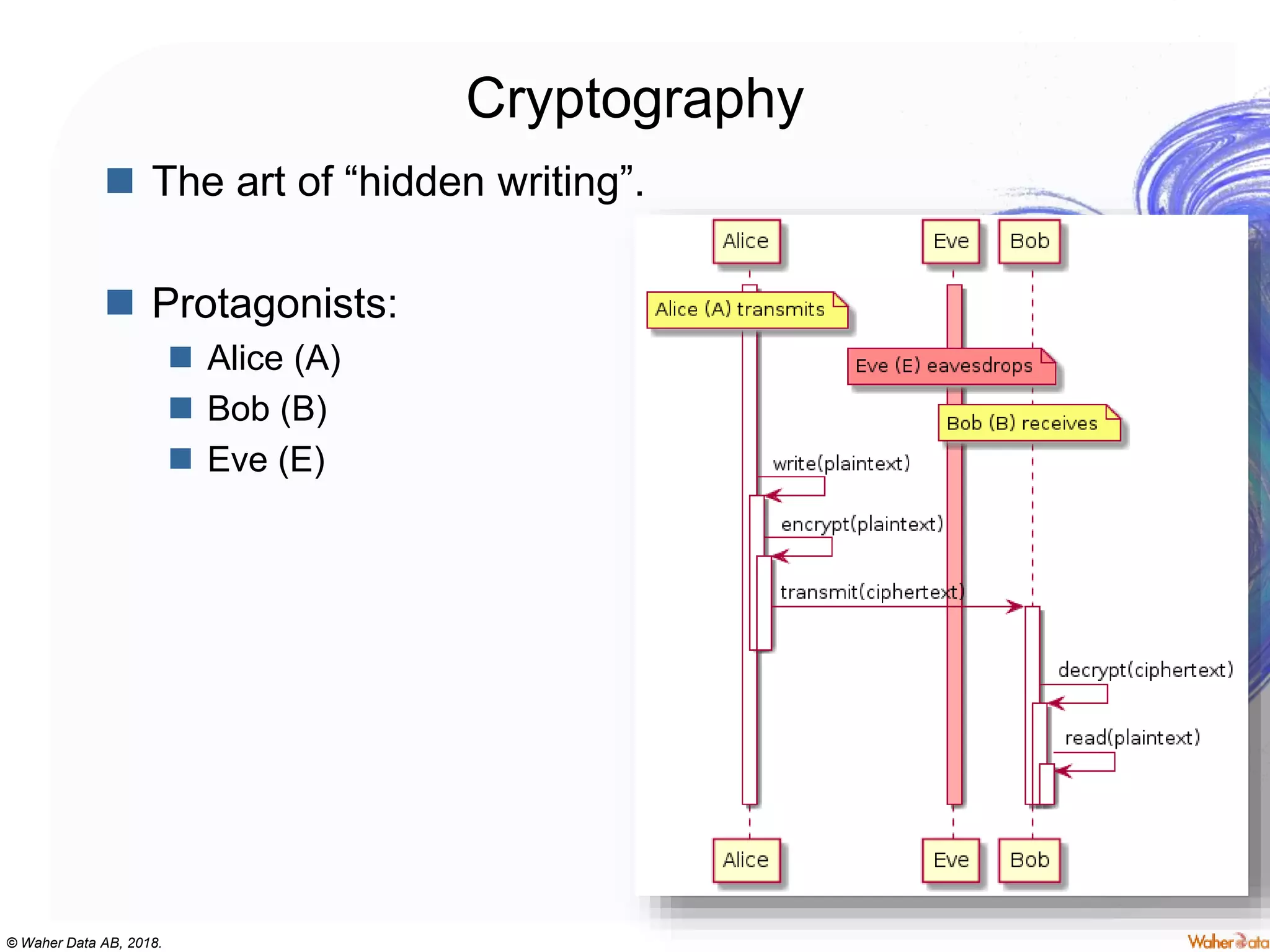
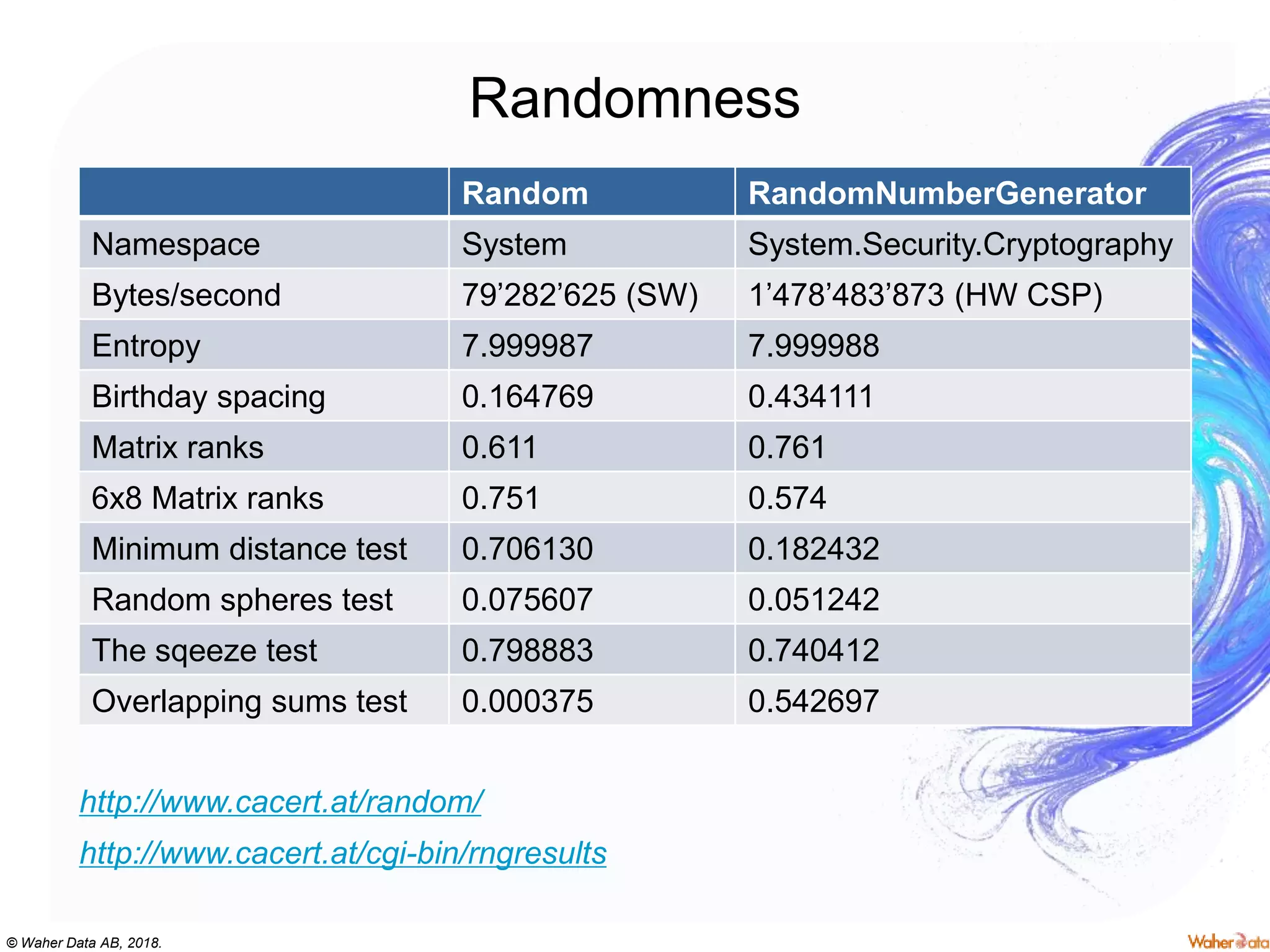
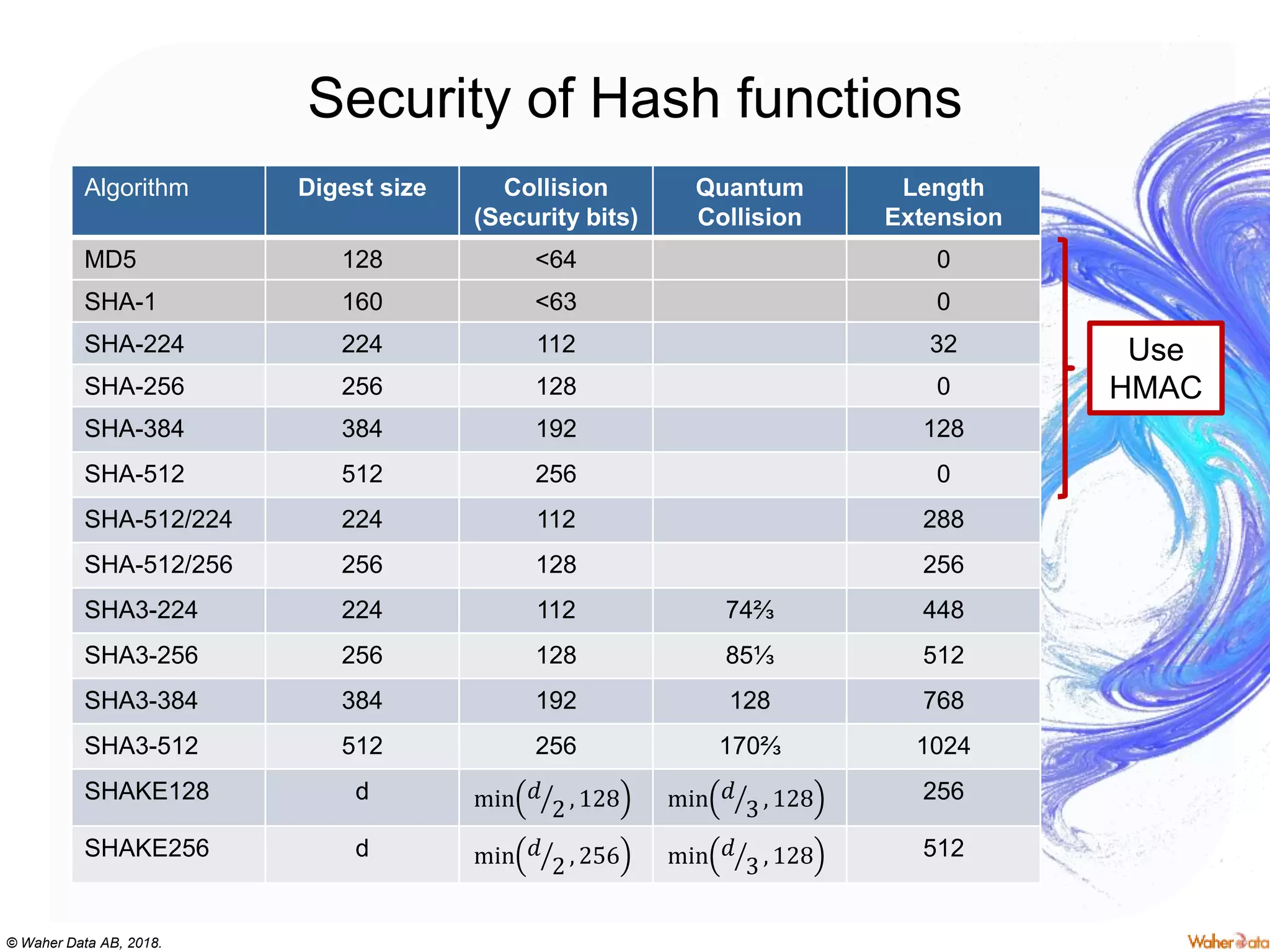
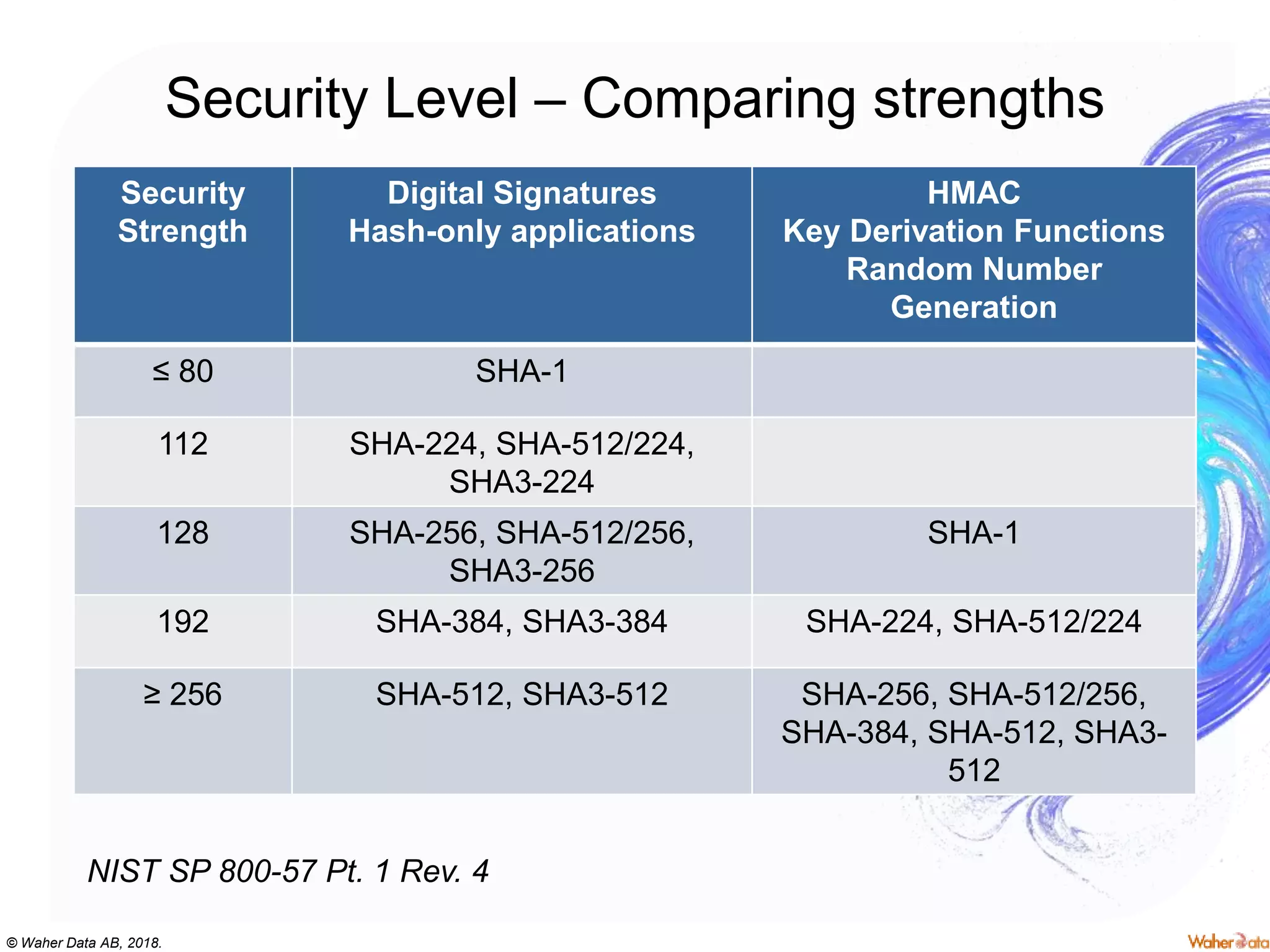
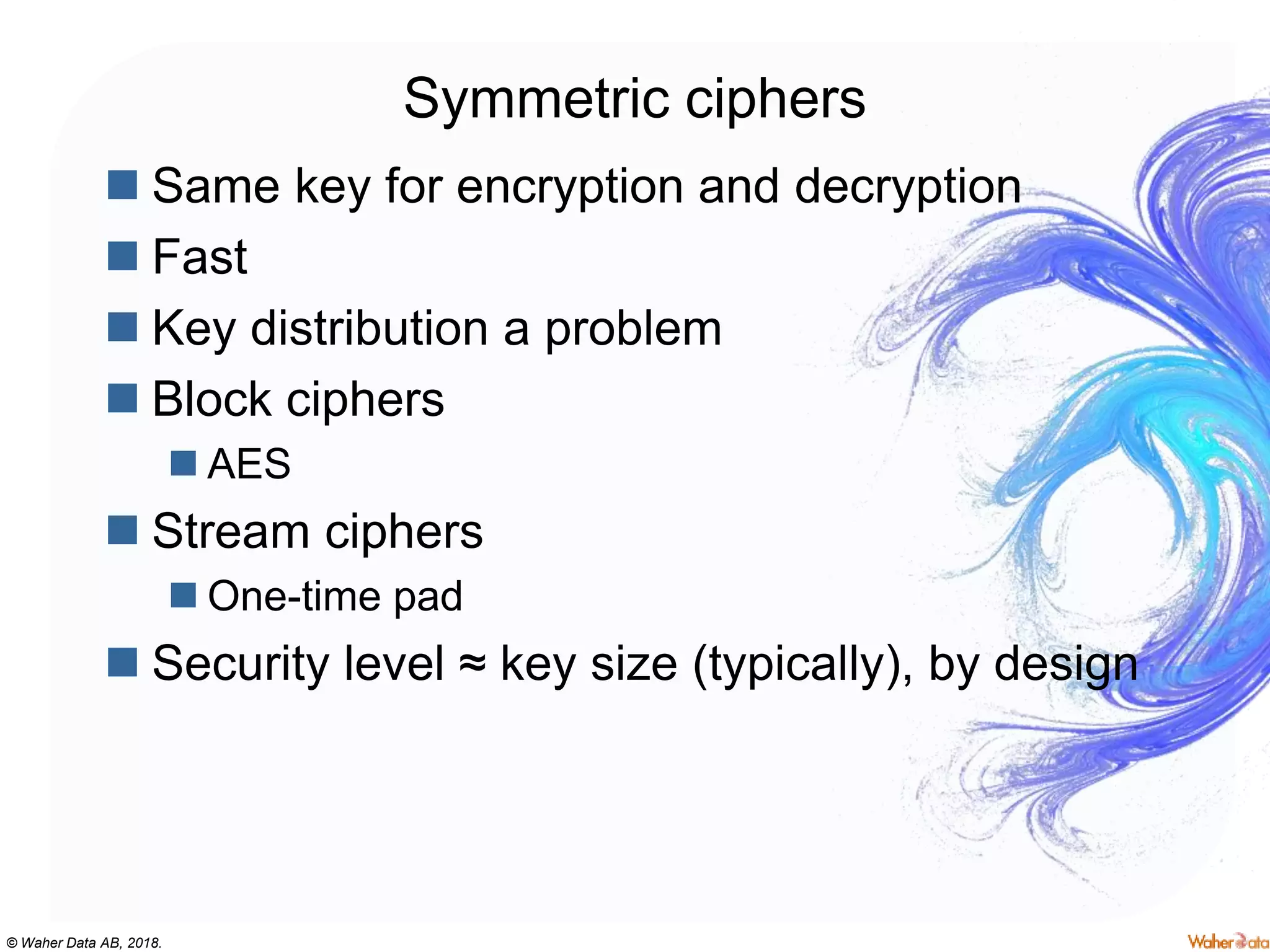
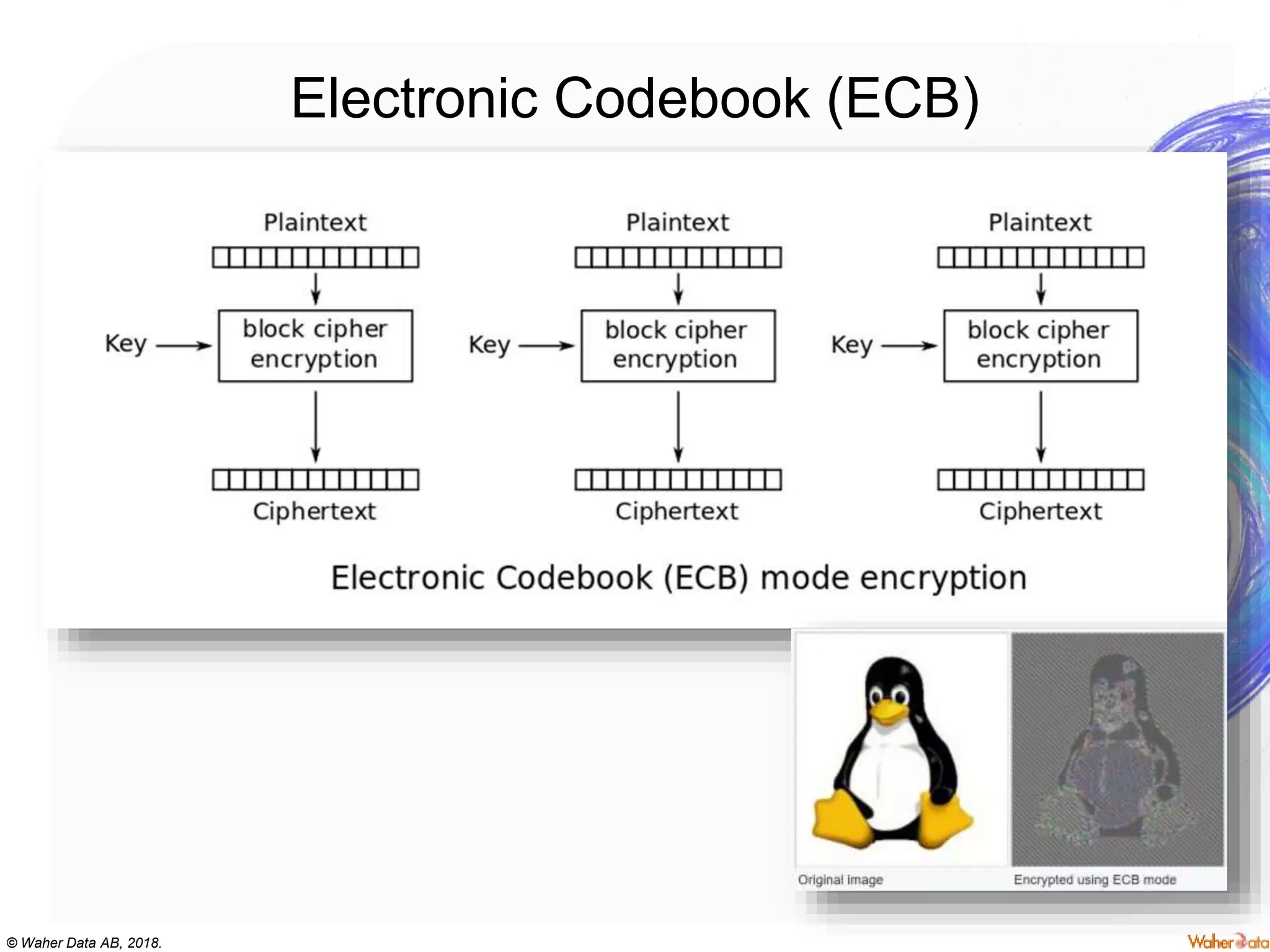
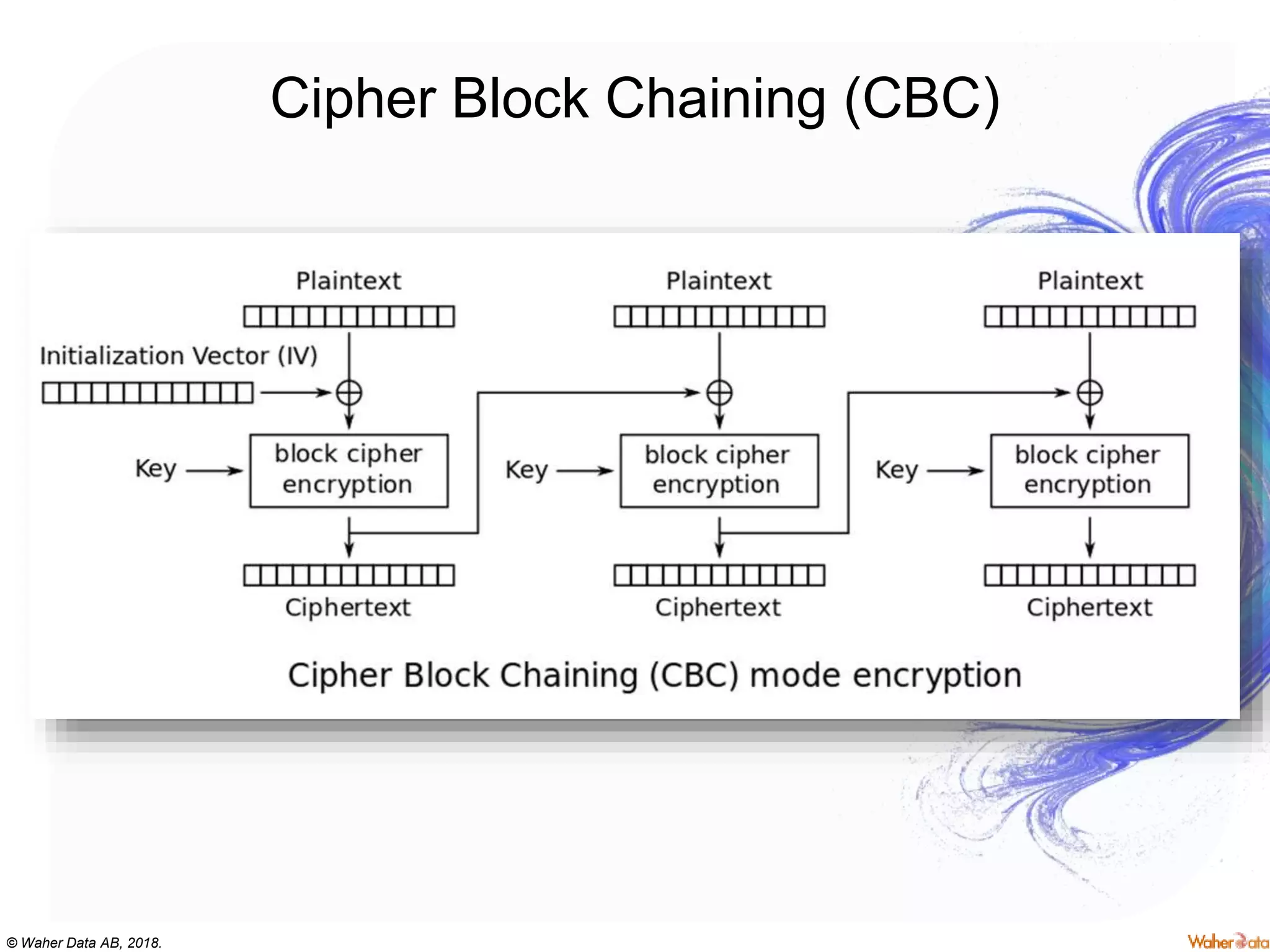
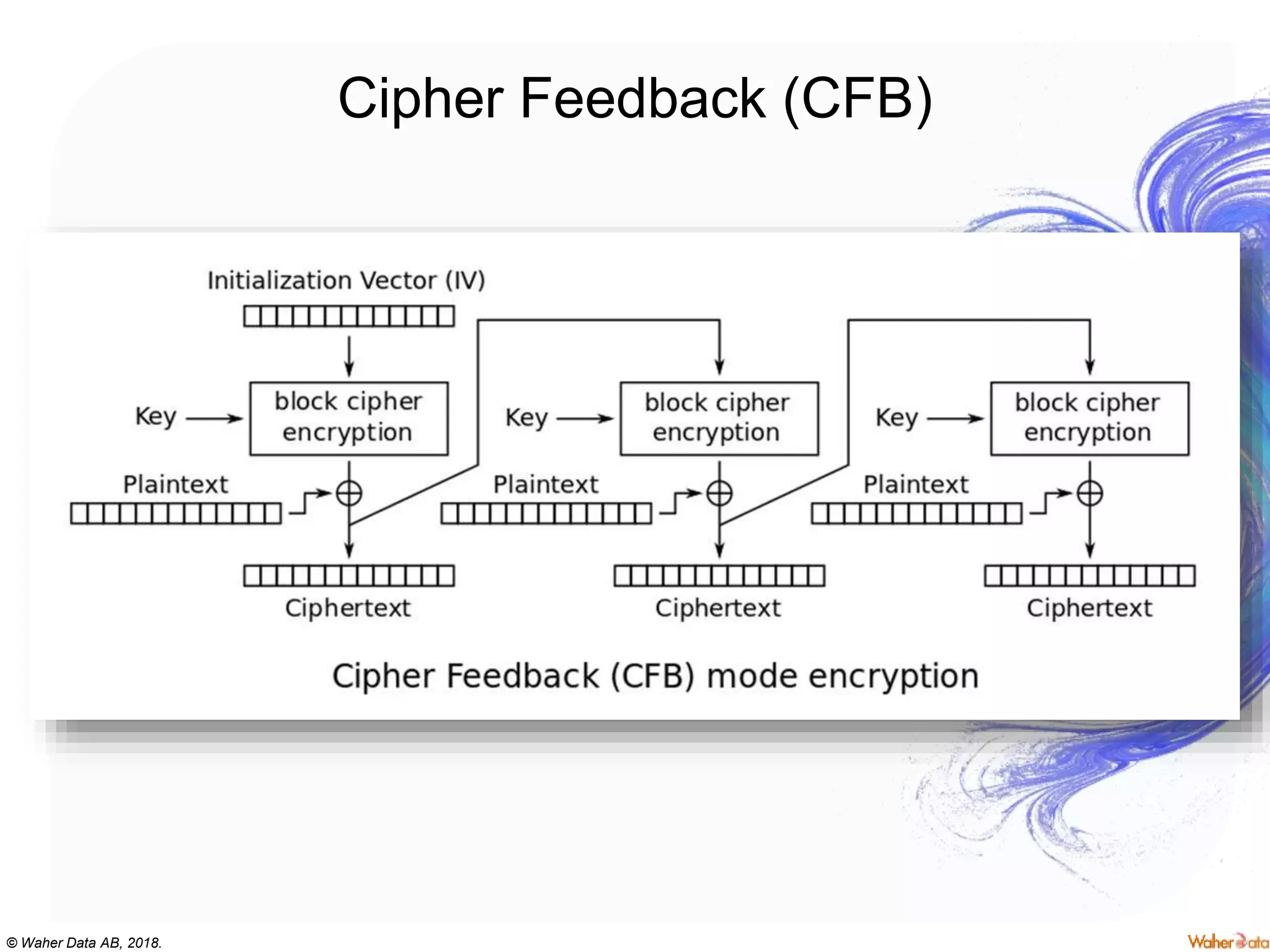
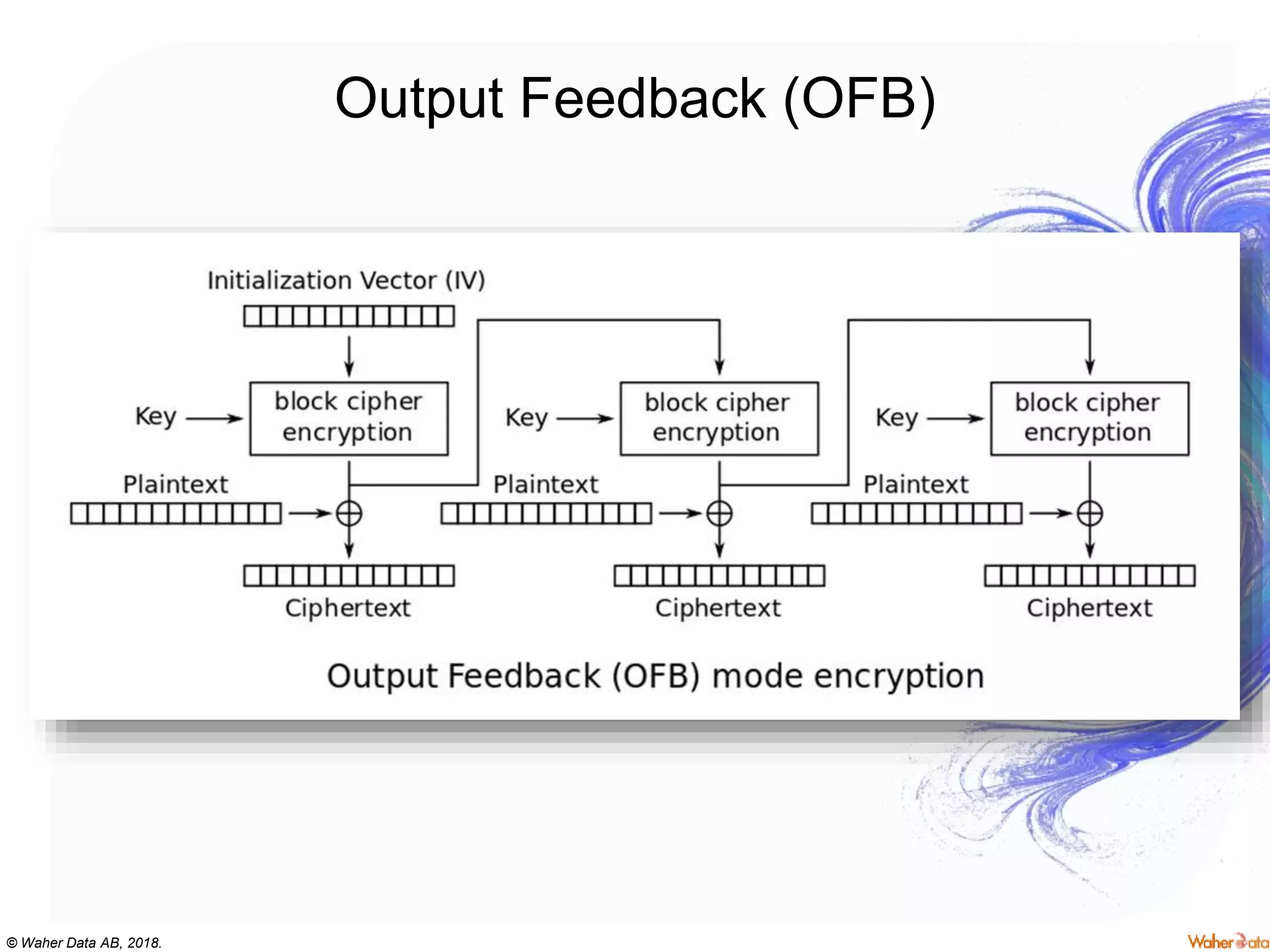
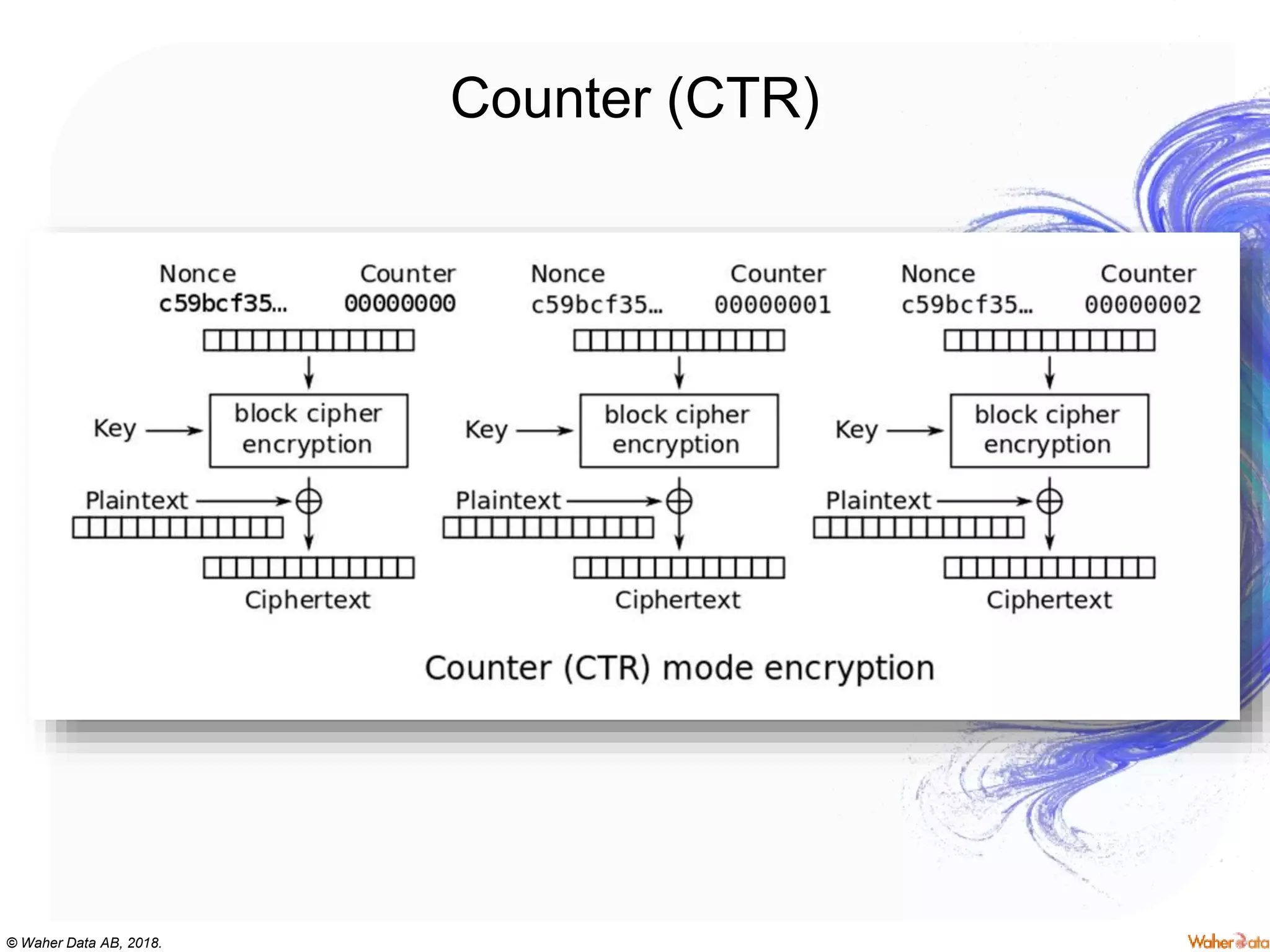
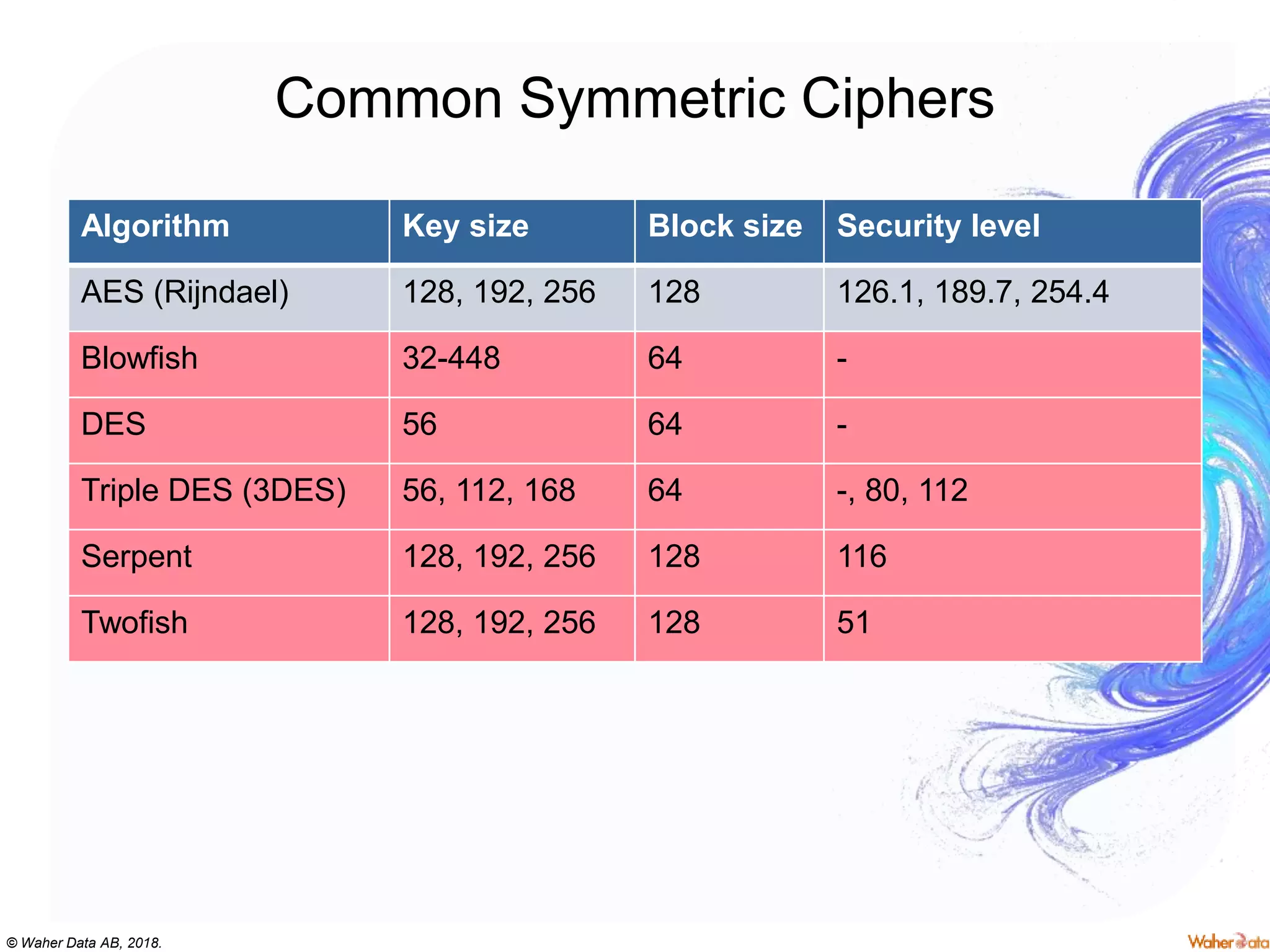
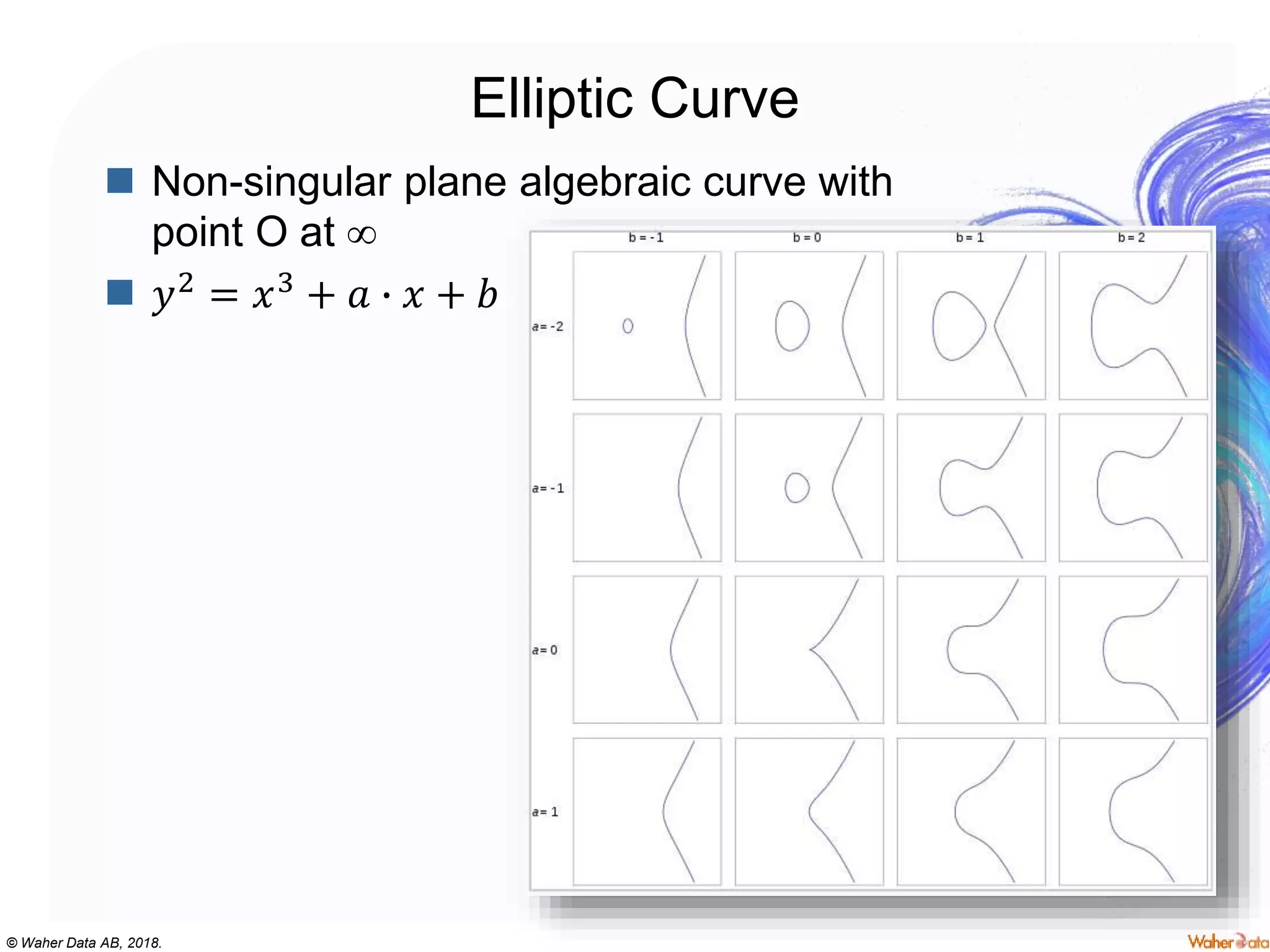
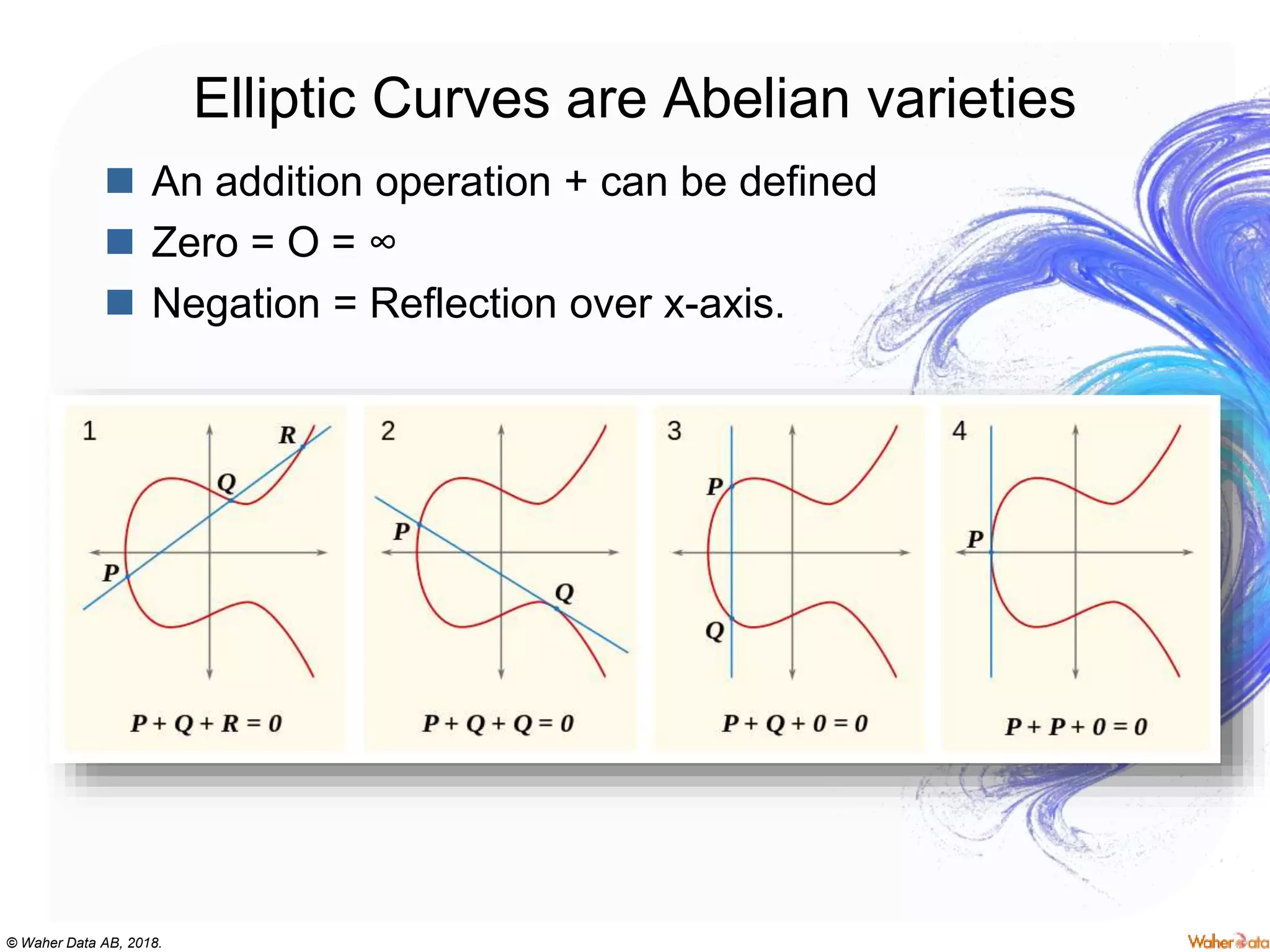
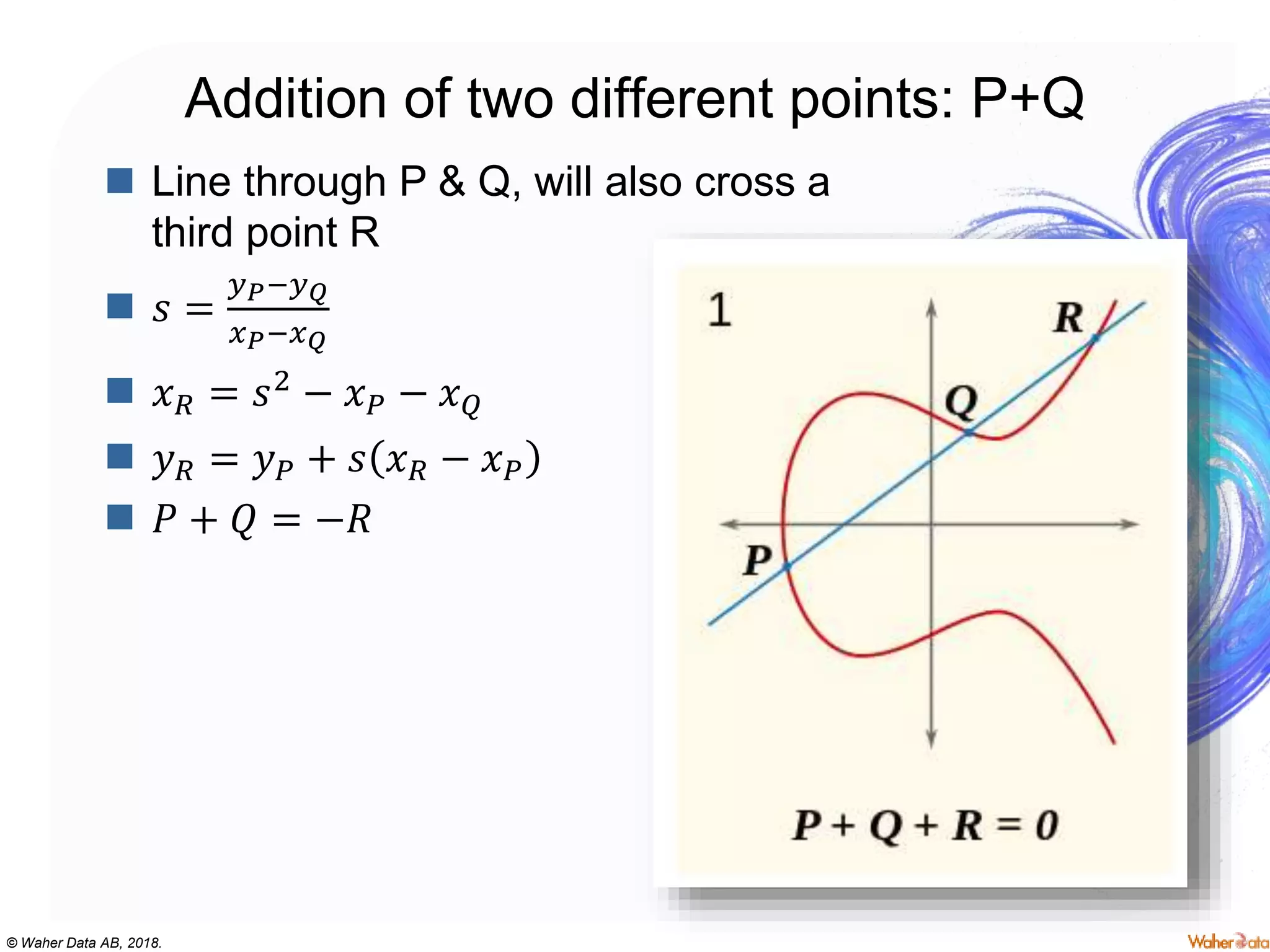
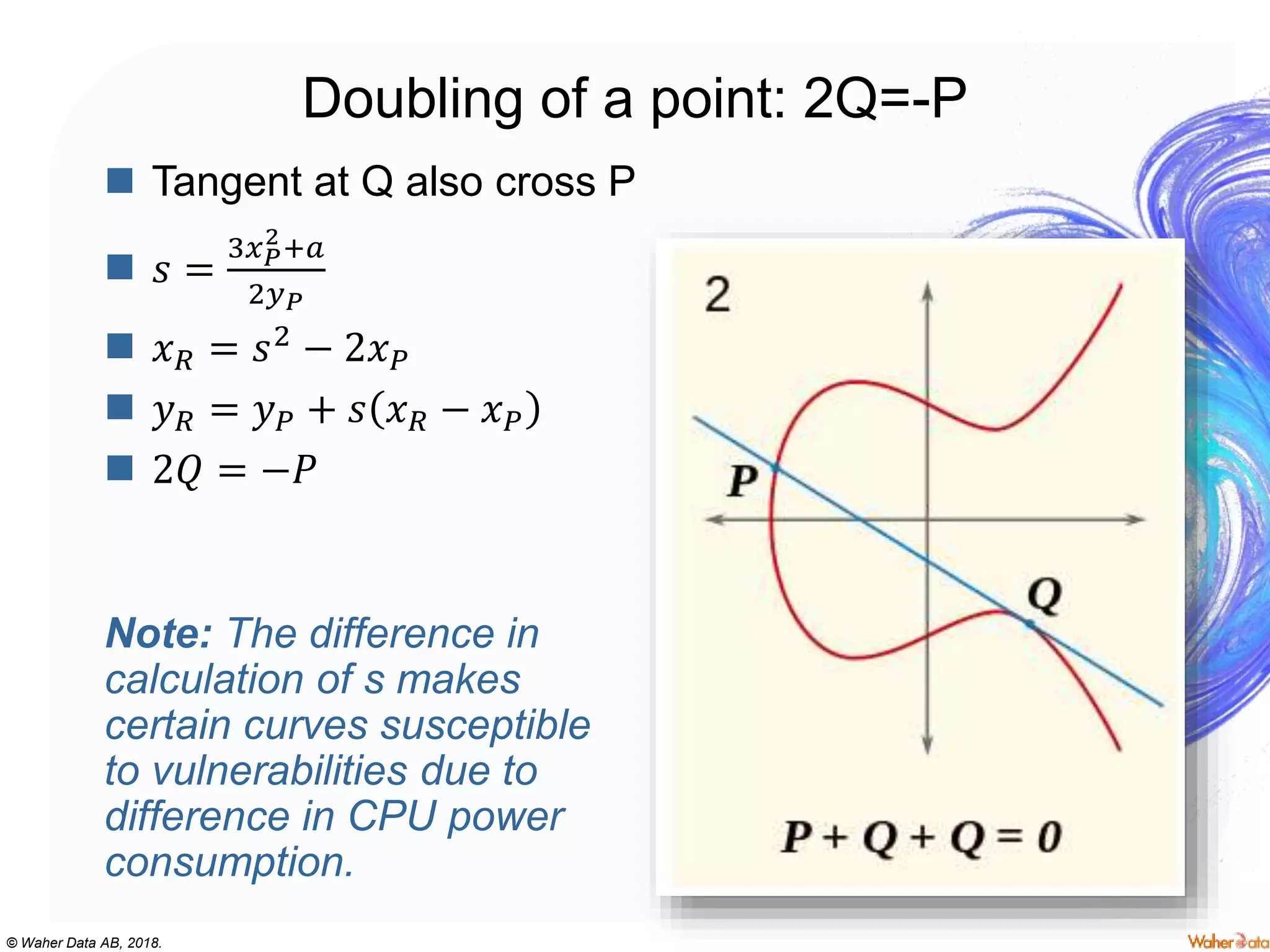
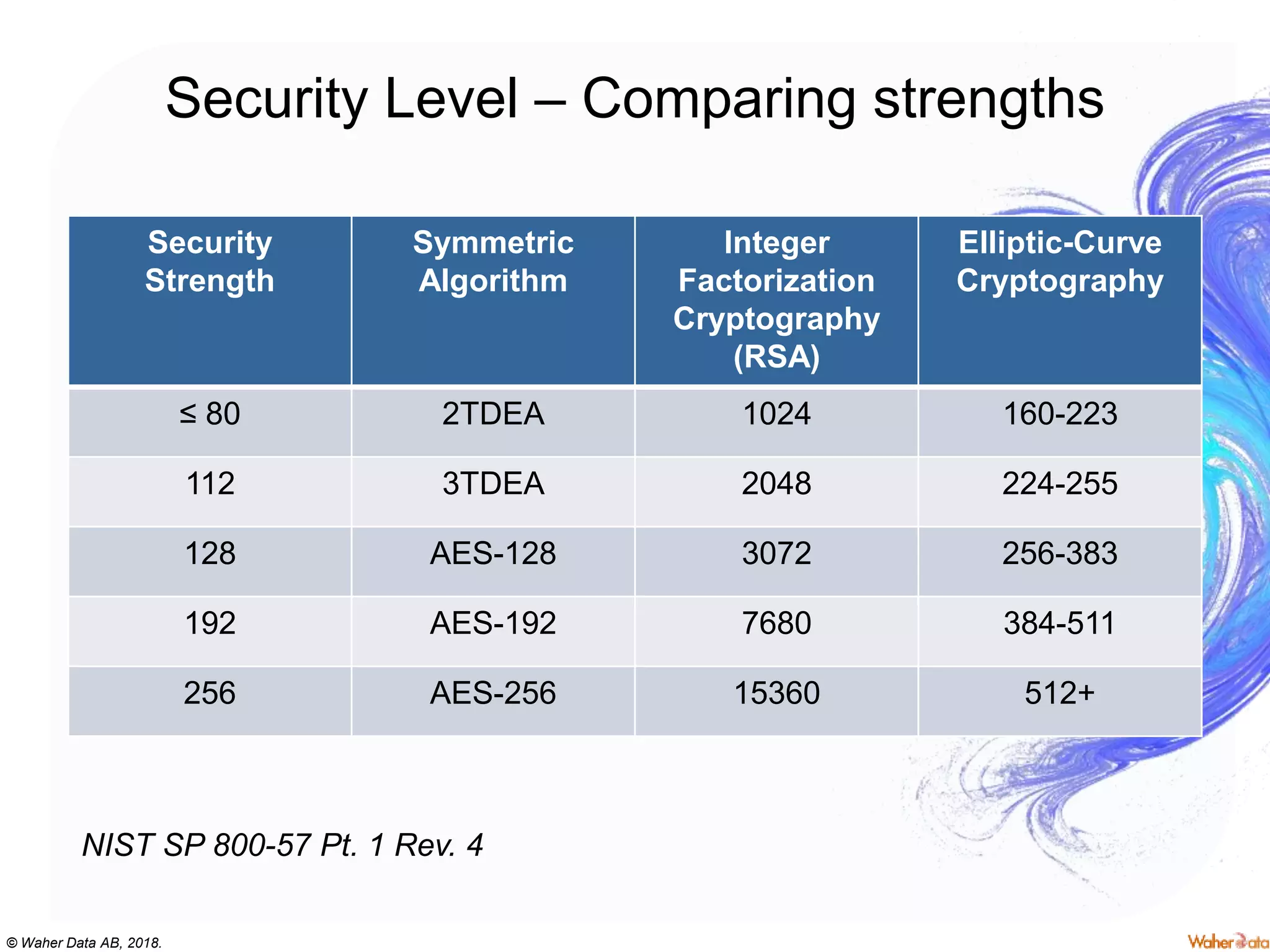
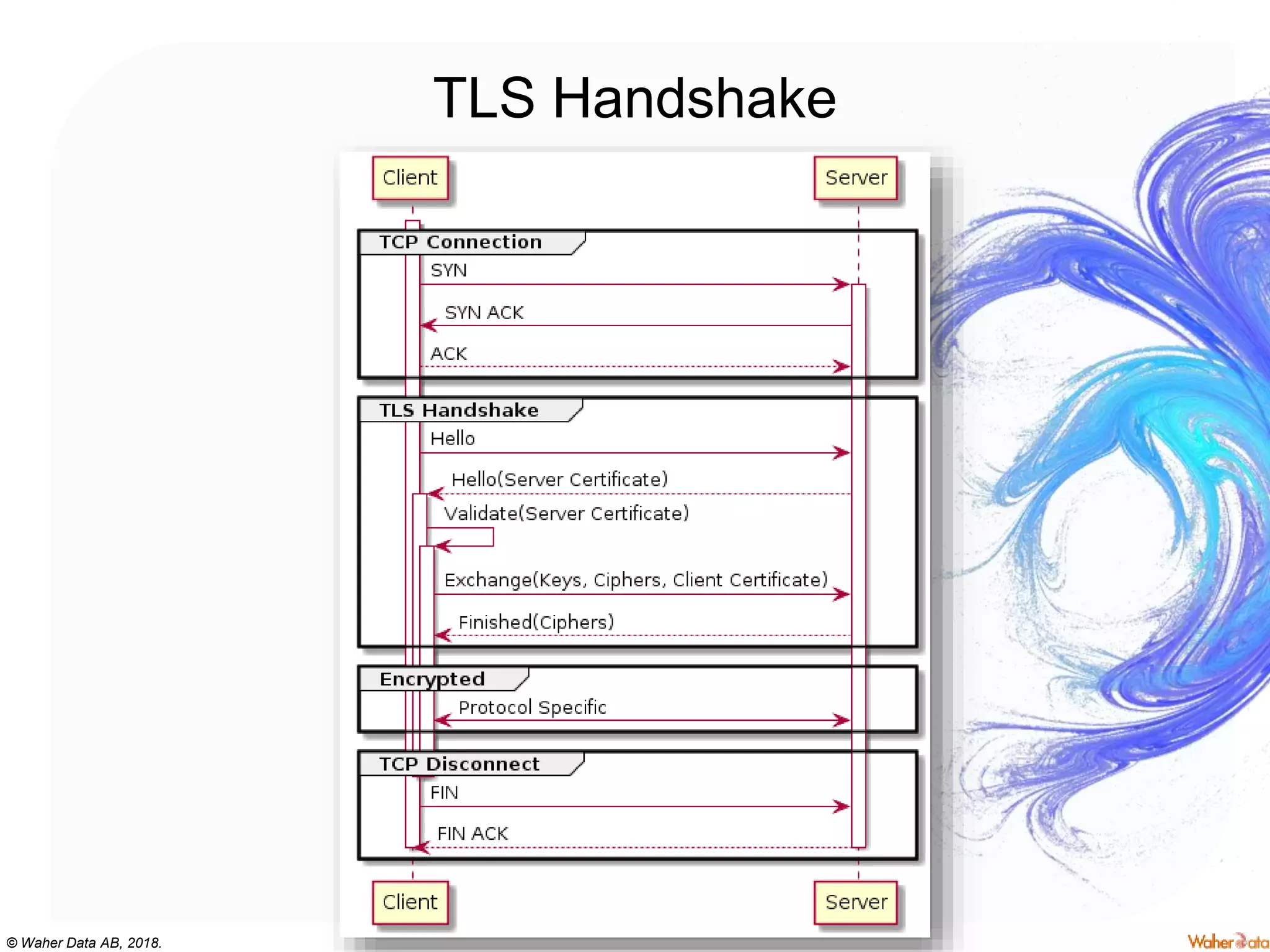
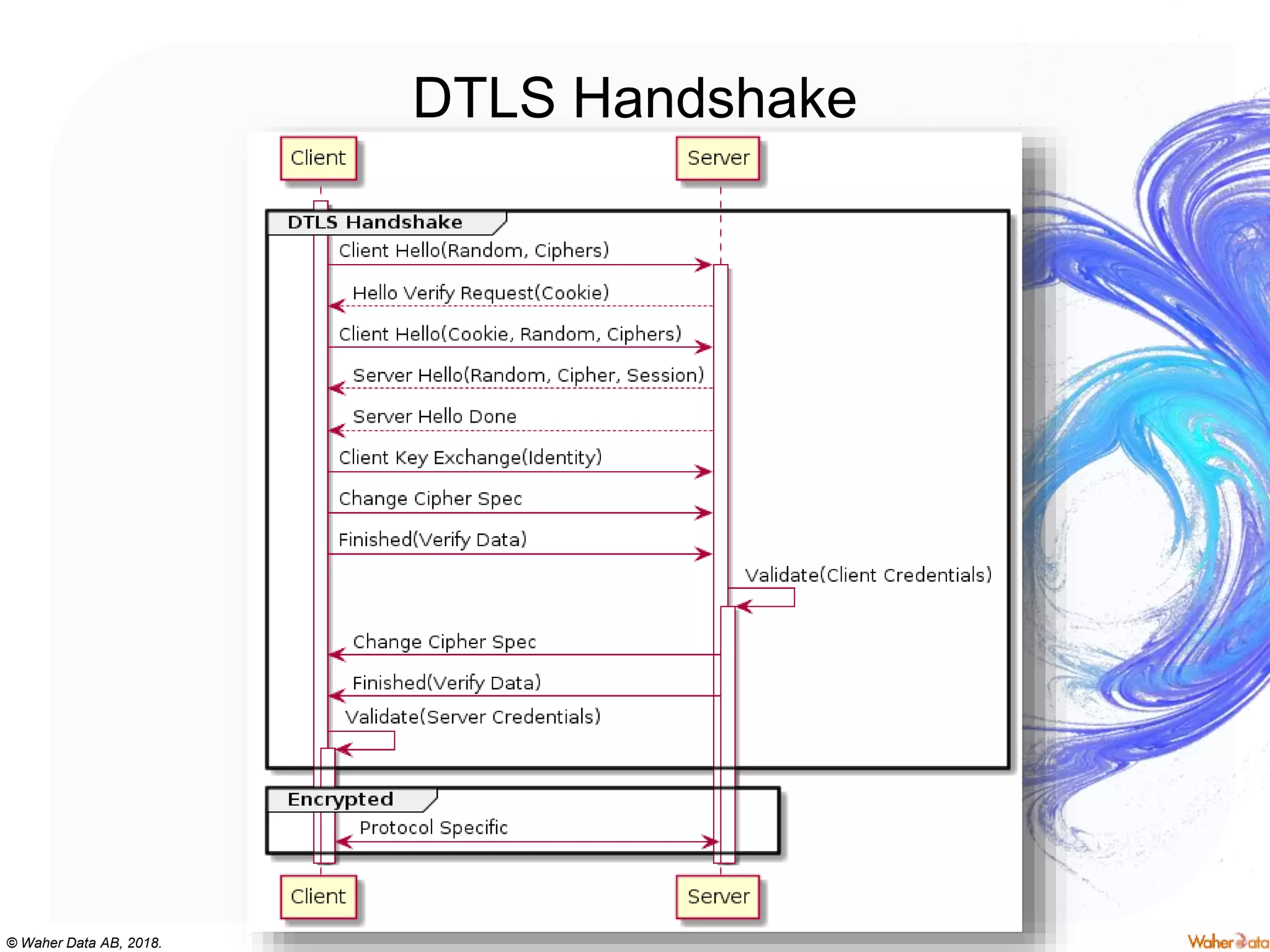
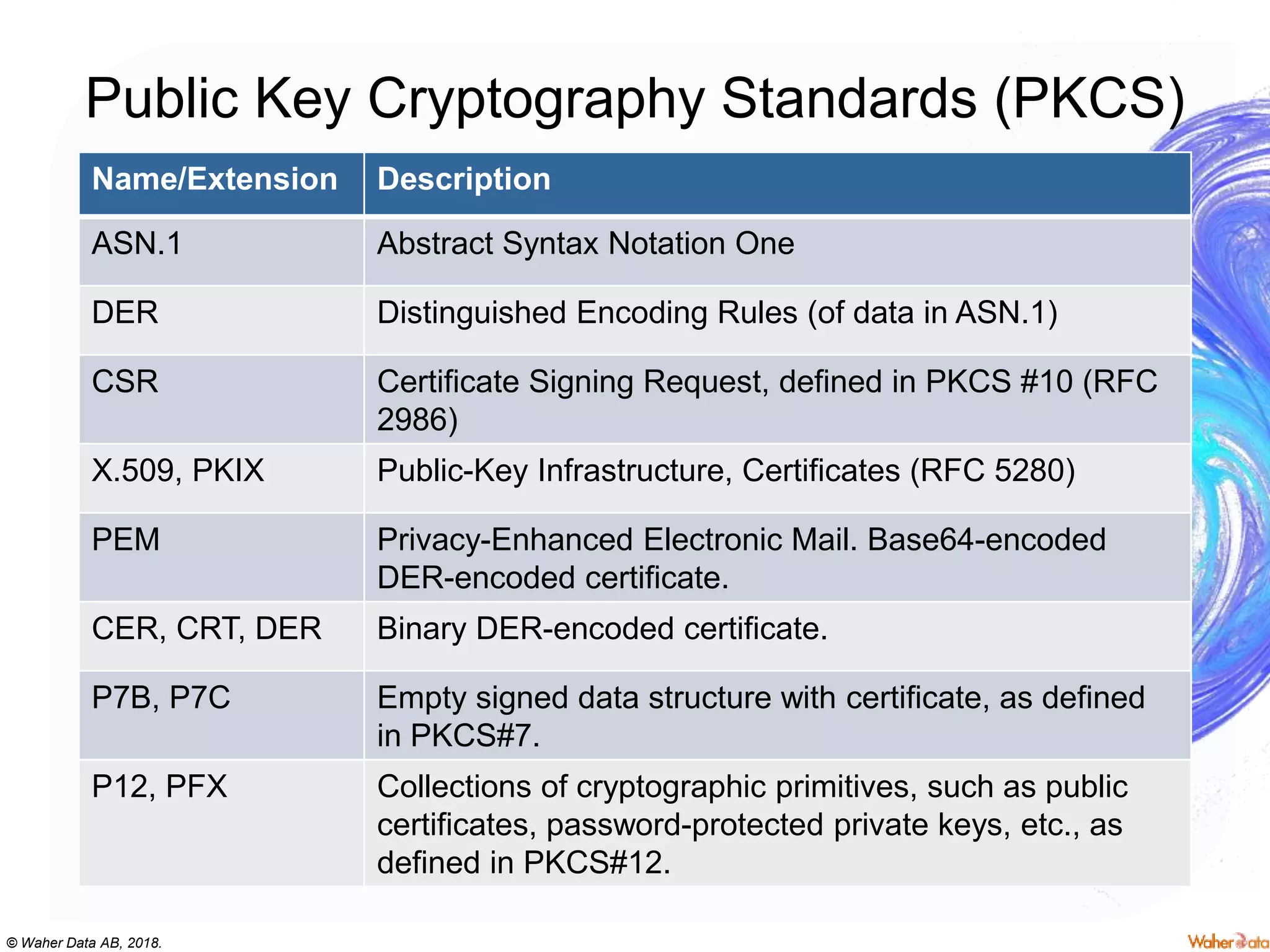
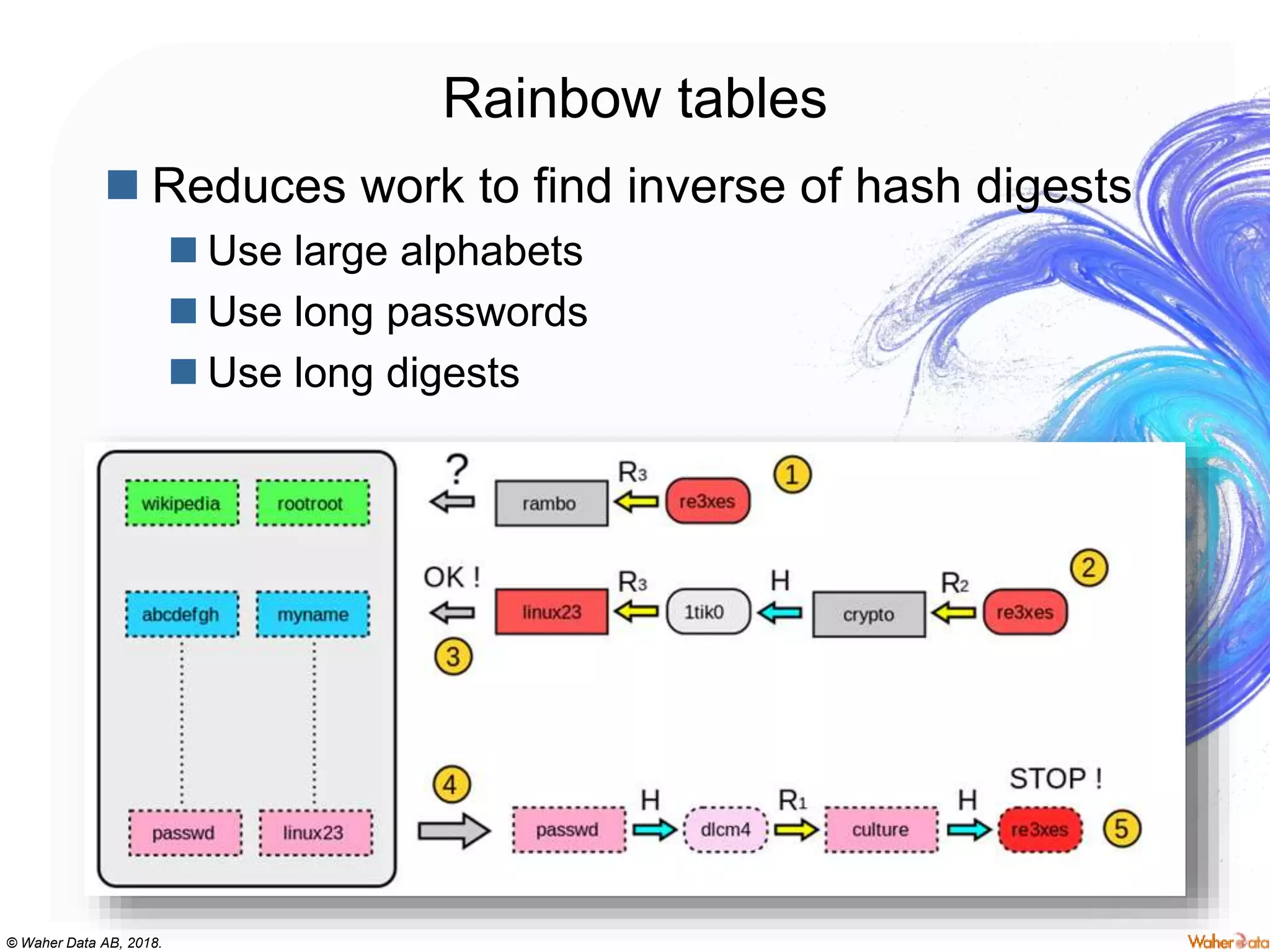
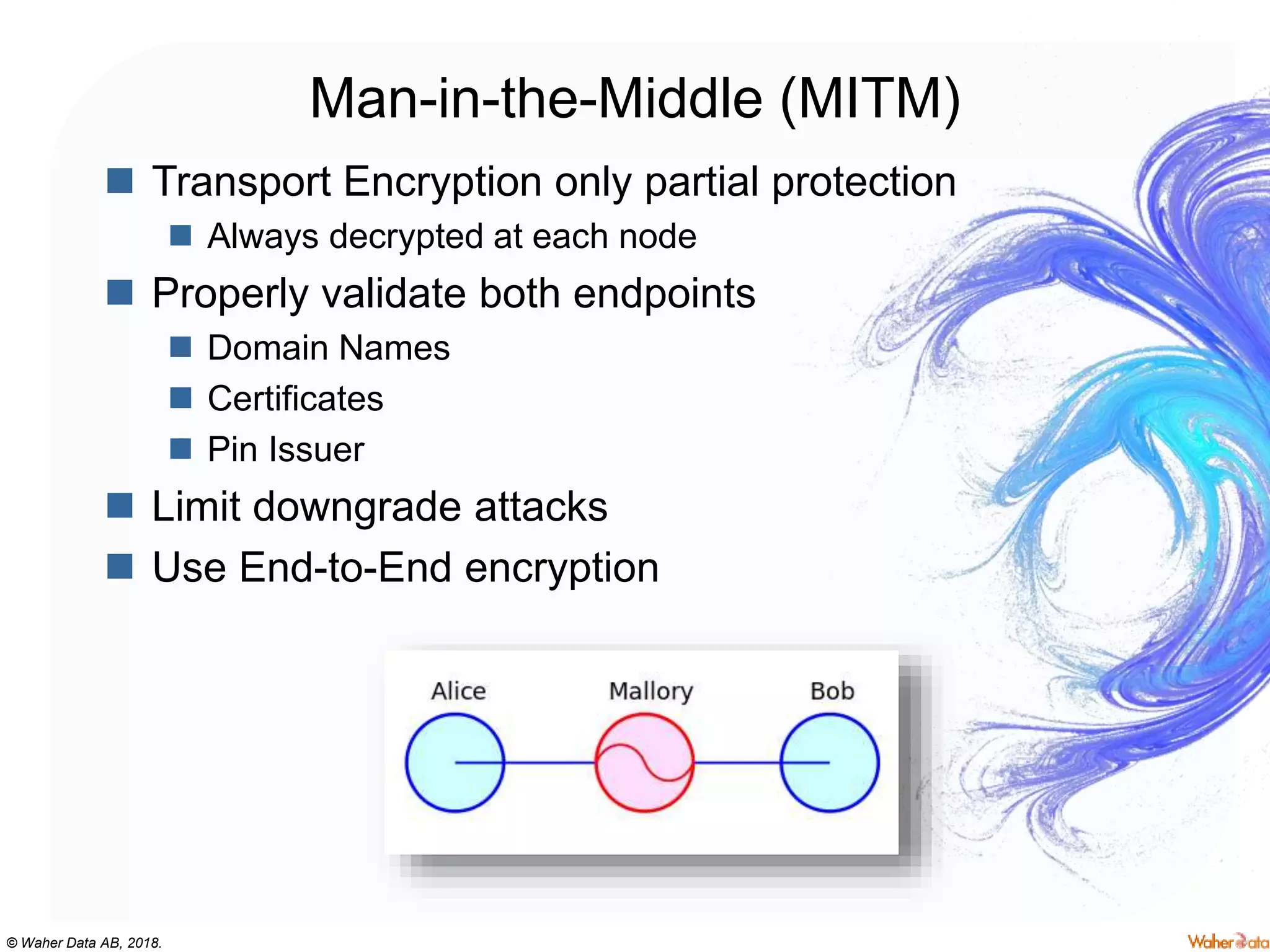
The document provides an extensive overview of cryptography, covering concepts such as symmetric and asymmetric ciphers, hash functions, and their applications in securing communications. It discusses both historic and modern methods, detailing cryptographic operations, random number generation, and the significance of various encryption standards like AES and RSA. Additionally, it highlights key features of Transport Layer Security (TLS) and emphasizes the importance of security protocols in ensuring data integrity and confidentiality.

1. © Waher Data AB, 2018.
Smart City Lecture 5
Introduction to Encryption

2. © Waher Data AB, 2018.
1. Introduction

3. © Waher Data AB, 2018.
Cryptography
 The art of “hidden writing”.
 Protagonists:
 Alice (A)
 Bob (B)
 Eve (E)

4. © Waher Data AB, 2018.
Historic methods
 Substitution ciphers
 Vulnerable to frequency analysis
 Rotor cipher machines
 Polyalphabetic ciphers
 One-time pads
 Cryptographically secure (or as
secure as you keep the pad).
 “perfect secrecy” (immune to brute
force attacks)
cf. Infinite Monkey Theorem
 C = P ⴲ R (XOR, modular addition)
 Code books

5. © Waher Data AB, 2018.
Computerized methods
 Mathematical problems that are difficult to
solve (today)
 Integer factorization
 Discrete logarithm problem (DLP)
 Elliptic curve discrete logarithm problem (ECDLP)
 Symmetrical ciphers
 Same key used for encryption and decryption (ex:
AES)
 Asymmetrical ciphers
 Different keys used for encryption and decryption
(ex: RSA)

6. © Waher Data AB, 2018.
Cryptographic Operations
 Pseudo-random number generation
 Hash functions
 Encryption
 Decryption
 Validation / Signatures
 Key distribution

7. © Waher Data AB, 2018.
2. Random Numbers

8. © Waher Data AB, 2018.
Motivation
 Stream ciphers
 One-time pads
 Cryptographically secure (or as secure as you keep
the pad).
 “perfect secrecy” (immune to brute force attacks)
 C = P ⴲ R (XOR, modular addition)
 Code books
 Also
 Simulation
 Statistical analysis

9. © Waher Data AB, 2018.
Randomness
Random RandomNumberGenerator
Namespace System System.Security.Cryptography
Bytes/second 79’282’625 (SW) 1’478’483’873 (HW CSP)
Entropy 7.999987 7.999988
Birthday spacing 0.164769 0.434111
Matrix ranks 0.611 0.761
6x8 Matrix ranks 0.751 0.574
Minimum distance test 0.706130 0.182432
Random spheres test 0.075607 0.051242
The sqeeze test 0.798883 0.740412
Overlapping sums test 0.000375 0.542697
http://www.cacert.at/random/
http://www.cacert.at/cgi-bin/rngresults

10. © Waher Data AB, 2018.
3. Hash Functions

11. © Waher Data AB, 2018.
Cryptographic Hash functions
 Variable length message ↦
Fixed length digest
 𝐷 = H 𝑚
 Deterministic
 Same input ↦ Same output
 Instable
 Small change in input ↦
Large change in output
 Not invertible
 Infeasible to find an input given a digest…

12. © Waher Data AB, 2018.
Applications
 Signatures
 Verifying integrity of messages/files
 Password management
 Verifying passwords
 Storing hashes instead of passwords
 Proof of work
Authentication
Block chain
 Pseudo-Random Functions

13. © Waher Data AB, 2018.
Common Hash functions
Function Digest
MD4 obsolete, 128 bit digest
MD5 obsolete, 128 bit digest
SHA-1 obsolete , 160 bit digest
SHA-2 224, 256, 384, 512 bit digests
SHA-3 224, 256, 384, 512, variable bit digests

14. © Waher Data AB, 2018.
Security of Hash functions
Algorithm Digest size Collision
(Security bits)
Quantum
Collision
Length
Extension
MD5 128 <64 0
SHA-1 160 <63 0
SHA-224 224 112 32
SHA-256 256 128 0
SHA-384 384 192 128
SHA-512 512 256 0
SHA-512/224 224 112 288
SHA-512/256 256 128 256
SHA3-224 224 112 74⅔ 448
SHA3-256 256 128 85⅓ 512
SHA3-384 384 192 128 768
SHA3-512 512 256 170⅔ 1024
SHAKE128 d min 𝑑
2 , 128 min 𝑑
3 , 128 256
SHAKE256 d min 𝑑
2 , 256 min 𝑑
3 , 128 512
Use
HMAC

15. © Waher Data AB, 2018.
HMAC
 “Message Authentication Codes (MAC) based on
cryptographic hash (H) functions.”
 Solves Length Extension Vulnerability
 Produces different hashes for same content in
different context
 Uses a secret key: 𝐾
 𝐾′ =
pad 𝐾 len(𝐾) < len 𝐻
𝐾 len(𝐾) = len 𝐻
H(𝐾) len(𝐾) > len 𝐻
 HMAC 𝐾, 𝑚 = H 𝐾′ⴲ𝑜𝑝𝑎𝑑 ∥ H 𝐾′ⴲ𝑖𝑝𝑎𝑑 ∥ 𝑚
RFC 2104: Keyed Hashing for Message Authentication

16. © Waher Data AB, 2018.
Security Level – Comparing strengths
Security
Strength
Digital Signatures
Hash-only applications
HMAC
Key Derivation Functions
Random Number
Generation
≤ 80 SHA-1
112 SHA-224, SHA-512/224,
SHA3-224
128 SHA-256, SHA-512/256,
SHA3-256
SHA-1
192 SHA-384, SHA3-384 SHA-224, SHA-512/224
≥ 256 SHA-512, SHA3-512 SHA-256, SHA-512/256,
SHA-384, SHA-512, SHA3-
512
NIST SP 800-57 Pt. 1 Rev. 4

17. © Waher Data AB, 2018.
4. Symmetric Ciphers

18. © Waher Data AB, 2018.
Symmetric ciphers
 Same key for encryption and decryption
 Fast
 Key distribution a problem
 Block ciphers
 AES
 Stream ciphers
 One-time pad
 Security level ≈ key size (typically), by design

19. © Waher Data AB, 2018.
Block Ciphers
 Operate on fixed sized blocks
 “Block Size”
 Block Cipher Mode (of operation on multiple
blocks)
 To provide secrecy across blocks.
 Initiation Vector (IV)
 Must be specified, and unpredictable.
 Padding

20. © Waher Data AB, 2018.
Electronic Codebook (ECB)

21. © Waher Data AB, 2018.
Cipher Block Chaining (CBC)

22. © Waher Data AB, 2018.
Cipher Feedback (CFB)

23. © Waher Data AB, 2018.
Output Feedback (OFB)

24. © Waher Data AB, 2018.
Counter (CTR)

25. © Waher Data AB, 2018.
Common Symmetric Ciphers
Algorithm Key size Block size Security level
AES (Rijndael) 128, 192, 256 128 126.1, 189.7, 254.4
Blowfish 32-448 64 -
DES 56 64 -
Triple DES (3DES) 56, 112, 168 64 -, 80, 112
Serpent 128, 192, 256 128 116
Twofish 128, 192, 256 128 51

26. © Waher Data AB, 2018.
AES (Advanced Encryption Standard)
 FIPS PUB 197 (Federal Information
Processing Standard)
 Block Cipher
 Matrix operations
 Fast
 Hardware support
 Few vulnerabilities found (in algorithm).
 Input:
 Key, 128, 192, 256 bits (= key size)
 Initiation Vector (IV), always 128 bits (= block size)

27. © Waher Data AB, 2018.
5. Asymmetric Ciphers

28. © Waher Data AB, 2018.
Asymmetric ciphers
 Public Key Cryptography
One public key, for:
Encryption
Validation of signature
 One private key, for:
Decryption
Signing
 Slow
 Solves key distribution problem
 RSA (Rivest-Shamir-Adleman)
 ECC (Elliptic Curve Cryptography)

29. © Waher Data AB, 2018.
RSA (Rivest-Shamir-Adleman)
 Choose two primes 𝑝, 𝑞.
 Calculate modulus: 𝒏 = 𝒑 ∙ 𝒒 cf. “bit key size”
 Select public exponent 𝑒 typically 216 + 1
 Calculate: ∃𝑑: 𝑑 ∙ 𝑒 ≡ 1(mod λ 𝑛 ) λ 𝑛 = lcm 𝑝 − 1, 𝑞 − 1
 Public key: 𝑛, 𝑒
 Private key: 𝑝, 𝑞, 𝑑
 Encryption: 𝑐 ≡ 𝑚 𝑒(mod 𝑛) 𝒎 ≡ 𝐩𝐚𝐝 𝑴 (𝐦𝐨𝐝 𝒏)
 Decryption: 𝑐 𝑑 ≡ 𝒎 𝒆 𝒅 ≡ 𝒎 𝒆∙𝒅 ≡ 𝒎 𝟏 ≡ 𝑚 (mod 𝑛)
 Sign: 𝑆 ≡ H 𝑚 𝑑 (mod 𝑛)
 Verify: 𝑆 𝑒 ≡ H 𝑚 𝑑 𝑒
≡ H 𝑚 𝑑∙𝑒 ≡ H 𝑚 1 ≡ H 𝑚 (mod 𝑛)

30. © Waher Data AB, 2018.
RSA - Properties
 Large keys (use at least 3072 bit key sizes)
 Slow
 Based on (believed) difficulty of
 Integer factorization
 Discrete Logarithm problem (DLP)
 Vulnerabilities
 Choice of primes and exponents
 Sending the same plain text to many recipients should be
avoided, even if they have different keys, but use same
exponent e.
 RSA without padding is not semantically secure.
 Use OAEP padding (PKCS#1 v1.5 and earlier not secure).
 Chinese Remainder Theorem: Precomputes 𝑑 𝑃, 𝑑 𝑄,
𝑞𝑖𝑛𝑣

31. © Waher Data AB, 2018.
Elliptic Curve Cryptography (ECC)
 Uses Elliptic Curves over Finite Fields
 Smaller Keys compared to RSA
 Faster than RSA
(for the same security level)
 Mathematics more difficult
(or more unknown)
 Security level difficult to determine
 Different curves have different properties
 Some require different implementations
 “Elliptic” comes from the study of arc lengths
of ellipses.

32. © Waher Data AB, 2018.
Elliptic Curve
 Non-singular plane algebraic curve with
point O at ∞
 𝑦2 = 𝑥3 + 𝑎 ∙ 𝑥 + 𝑏

33. © Waher Data AB, 2018.
Elliptic Curves are Abelian varieties
 An addition operation + can be defined
 Zero = O = ∞
 Negation = Reflection over x-axis.

34. © Waher Data AB, 2018.
Addition of two different points: P+Q
 Line through P & Q, will also cross a
third point R
 𝑠 =
𝑦 𝑃−𝑦 𝑄
𝑥 𝑃−𝑥 𝑄
 𝑥 𝑅 = 𝑠2 − 𝑥 𝑃 − 𝑥 𝑄
 𝑦 𝑅 = 𝑦 𝑃 + 𝑠 𝑥 𝑅 − 𝑥 𝑃
 𝑃 + 𝑄 = −𝑅

35. © Waher Data AB, 2018.
Doubling of a point: 2Q=-P
 Tangent at Q also cross P
 𝑠 =
3𝑥 𝑃
2
+𝑎
2𝑦 𝑃
 𝑥 𝑅 = 𝑠2 − 2𝑥 𝑃
 𝑦 𝑅 = 𝑦 𝑃 + 𝑠 𝑥 𝑅 − 𝑥 𝑃
 2𝑄 = −𝑃
Note: The difference in
calculation of s makes
certain curves susceptible
to vulnerabilities due to
difference in CPU power
consumption.

36. © Waher Data AB, 2018.
Defining a Prime Elliptic Curve for ECC
 𝑝 is a prime number.
 𝐶 defined over ℤ 𝑝
2 by parameters 𝑎 and 𝑏.
 integer arithmetic, modulus 𝑝.
 A generator (or base) point 𝐺𝜖𝐶 must be selected
properly.
 Order 𝑛 of 𝐺 computed: Smallest positive 𝑛 such that 𝑛 ∙ 𝐺 = 0
 Cofactor ℎ =
𝐸(𝔽 𝑝)
𝑛 small, preferably ℎ = 1
 Domain parameters: 𝑝, 𝑎, 𝑏, 𝐺, 𝑛, ℎ
 Must be validated
 Difficult to validate

37. © Waher Data AB, 2018.
What curves are safe?
 Several common curves not safe for
many different reasons.
 NIST recommended curves with
unexplained “magical constants”
provided by NSA.
 https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.
FIPS.186-4.pdf
 As a rule, all steps of a security algorithm
must be open and fully explained.
“Transparency”
 Before selecting a curve, check:
https://safecurves.cr.yp.to/

38. © Waher Data AB, 2018.
Elliptic-Curve Discrete Logarithm Problem
 Select a random number
𝑑 ∈ 1, 𝑛 − 1
 Let 𝑑 be your private key.
 Compute your public key:
𝑃 = 𝑑 ∙ 𝐺
 Finding 𝑑 from 𝑃 and 𝐺 is considered difficult.

39. © Waher Data AB, 2018.
Elliptic-Curve Diffie-Hellman (ECDH)
 Alice has private key 𝑑 𝐴 and public key 𝑃𝐴 = 𝑑 𝐴 ∙ 𝐺
 Bob has private key 𝑑 𝐵 and public key 𝑃𝐵 = 𝑑 𝐵 ∙ 𝐺
 Alice computes 𝑑 𝐴 ∙ 𝑃𝐵 = 𝑑 𝐴 ∙ 𝑑 𝐵 ∙ 𝐺 = 𝑃 = (𝑥, 𝑦)
 Bob computes 𝑑 𝐵 ∙ 𝑃𝐴 = 𝑑 𝐴 ∙ 𝑑 𝐵 ∙ 𝐺 = 𝑃 = (𝑥, 𝑦)
 𝑥 is now shared secret
 Apply appropriate Hash-function
to get correct bit-size: 𝐻(𝑥)

40. © Waher Data AB, 2018.
Elliptic-Curve Digital Signatures (ECDSA)
To sign:
 𝑒 = 𝐿 log2 𝐶 (𝐻 𝑚 )
 𝑘 ∈ 1, 𝑛 − 1 (random)
 𝑃1 = 𝑥1, 𝑦1 = 𝑘 ∙ 𝐺
 Check 𝑥1 ≠ 0
 𝑠 = 𝑘−1 𝑒 + 𝑥1 ∙ 𝑑 𝐴 (mod 𝑛)
 Check 𝑠 ≠ 0
 Signature is (𝑥1, 𝑠)
To verify:
 𝑒 = 𝐿 log2 𝐶 (𝐻 𝑚 )
 𝑤 = 𝑠−1 (mod 𝑛)
 𝑢1 = 𝑒 ∙ 𝑤 (mod 𝑛)
 𝑢2 = 𝑥1 ∙ 𝑤 (mod 𝑛)
 𝑃2 = 𝑥2, 𝑦2 = 𝑢1 ∙ 𝐺 + 𝑢2 ∙ 𝑃𝐴
 Check 𝑥1 = 𝑥2
Note: Order n of G must be prime.

41. © Waher Data AB, 2018.
6. Hybrid Ciphers

42. © Waher Data AB, 2018.
Combining ciphers
 Asymmetric ciphers
 Slow
 Efficient in public environments
 Symmetric ciphers
 Fast
 Problems with key distribution
 Two phase encryption
 Phase 1: Encrypt/agree on keys using asymmetric cipher
 Phase 2: Encrypt main payload using symmetric cipher

43. © Waher Data AB, 2018.
Security Level – Comparing strengths
Security
Strength
Symmetric
Algorithm
Integer
Factorization
Cryptography
(RSA)
Elliptic-Curve
Cryptography
≤ 80 2TDEA 1024 160-223
112 3TDEA 2048 224-255
128 AES-128 3072 256-383
192 AES-192 7680 384-511
256 AES-256 15360 512+
NIST SP 800-57 Pt. 1 Rev. 4

44. © Waher Data AB, 2018.
7. Additional Features

45. © Waher Data AB, 2018.
Forward Secrecy
 Compromise of session key does
not compromise past sessions
 Even if long-time private keys are used
 ECDHE has forward secrecy
 Keys generated at start of session.
 Last E = Ephemeral
(Elliptic Curve Diffie-Hellman
Ephemeral)

46. © Waher Data AB, 2018.
Deniability
 Keys used to authenticate sender
 Access to secret keys also proof of
sender
 Deniability is the ability to deny
being sender
 Publish hashed proof after receiver
has used it to authenticate sender
 cf. Off-the-Record Messaging (OTR)
https://otr.cypherpunks.ca/

47. © Waher Data AB, 2018.
8. Transport Layer
Security (TLS)

48. © Waher Data AB, 2018.
Transport Layer Security
 Protocol for negotiating ciphers and keys
 Loosely coupled / Pluggable
 TCP
 TLS
 UDP
 DTLS
 Current version: 1.3
 Avoid obsolete versions if possible.
 Avoid SSL (predecessor)

49. © Waher Data AB, 2018.
TLS Handshake

50. © Waher Data AB, 2018.
DTLS Handshake

51. © Waher Data AB, 2018.
Mutual TLS
 Server Certificate often mandatory
 Canonical Validation:
 Correlation with Domain Name in DNS lookup.
 Pin certificate
 Client Certificate optional
 No canonical validation.
 Manual configuration often required.
 Suitable for expensive/sensitive point-to-point
connections.
 Alternative: “Dialback”
 Canonical validation of client Domain Name
through DNS lookup.

52. © Waher Data AB, 2018.
Security Level
 Loose Coupling
 Examples: TLS, DTLS, X.509, SASL
 Pro:
 Can update ciphers as new more secure ciphers
become available
 Can obsolete vulnerable ciphers
 Avoids breaking protocol compatibility
 Con:
 Difficult to know what ciphers are actually being used
 Test TLS Security Level
 https://www.ssllabs.com/ssltest/
 https://github.com/ssllabs/research/wiki/SSL-Server-Rating-
Guide
 https://securityheaders.com/

53. © Waher Data AB, 2018.
Cipher Names
Names reveal algorithms combined to create cipher

54. © Waher Data AB, 2018.
9. Public Key
Infrastructure (PKI)

55. © Waher Data AB, 2018.
X.509 Certificates
 Collection of cryptographic primitives
 Cipher references
 Keys
 Signatures
 Identified by Object IDs (OID)
 Issuer
 Certificate Authority (CA)
 Subject
 Common Name
 Alternative Names

56. © Waher Data AB, 2018.
X.509 Certificate Chains
 Issuers identified by their own certificates
 Certificate without Issuer = Root
 Must be installed in operating system

57. © Waher Data AB, 2018.
Vulnerabilities
Avoid self-signed certificates!
 Vulnerable, if not rigorously protected.
 May leave unsecured code
 Never install self-signed certificates
Installed certificates must be properly
 Monitored
 Updated

58. © Waher Data AB, 2018.
Public Key Cryptography Standards (PKCS)
Name/Extension Description
ASN.1 Abstract Syntax Notation One
DER Distinguished Encoding Rules (of data in ASN.1)
CSR Certificate Signing Request, defined in PKCS #10 (RFC
2986)
X.509, PKIX Public-Key Infrastructure, Certificates (RFC 5280)
PEM Privacy-Enhanced Electronic Mail. Base64-encoded
DER-encoded certificate.
CER, CRT, DER Binary DER-encoded certificate.
P7B, P7C Empty signed data structure with certificate, as defined
in PKCS#7.
P12, PFX Collections of cryptographic primitives, such as public
certificates, password-protected private keys, etc., as
defined in PKCS#12.

59. © Waher Data AB, 2018.
Automated Certificate Management Environment
(ACME)
 Allows you to automate certificate
Creation
 Let’s Encrypt (Trusted CA)
 https://letsencrypt.org/
 ACME Endpoints:
 https://acme-v02.api.letsencrypt.org/directory
 https://acme-staging-v02.api.letsencrypt.org/directory
 Command-line tools
 Many libraries

60. © Waher Data AB, 2018.
10. Common forms of
attack

61. © Waher Data AB, 2018.
Rainbow tables
 Reduces work to find inverse of hash digests
 Use large alphabets
 Use long passwords
 Use long digests

62. © Waher Data AB, 2018.
Man-in-the-Middle (MITM)
 Transport Encryption only partial protection
 Always decrypted at each node
 Properly validate both endpoints
 Domain Names
 Certificates
 Pin Issuer
 Limit downgrade attacks
 Use End-to-End encryption

63. © Waher Data AB, 2018.
Side-Channel Attacks
 Exploits
 Erroneous assumptions
(Don’t assume you ever run in a protected
environment)
 Vulnerabilities in implementations
 Vulnerabilities in hardware
 Vulnerabilities in environment
 Examples:
 Timing attacks
 Cache attacks
 Power-monitoring attacks
 Data remanence

64. © Waher Data AB, 2018.
11. Other

65. © Waher Data AB, 2018.
Is it legal?
Well…
 Yes, for purely civil use
 What’s civil use?
 Not without permission
 for military use
 Depends… for “dual use”
 Export controls:
https://www.wassenaar.org/control-lists/
https://www.eff.org/issues/export-controls

66. © Waher Data AB, 2018.
Quantum Computing
 Post-quantum cryptography
 Quantum Turing Machine
Quantum Algorithms
Shor’s algorithm
(Integer factorization)
Simon’s algorithm
Probabilistic
Qubits
IBM (supposedly) has a 20 qubit
machine

67. © Waher Data AB, 2018.
12. Events

68. © Waher Data AB, 2018.
Smart City Lectures*
1. How to build a Smart City (Oct 4th)
2. Privacy in the Smart City (Oct 18th)
3. An Open and/or Secure Smart City (Oct 25th)
4. Harmonizing the Internet of Things (Nov 8th)
5. Introduction to Encryption (Nov 15th)
6. Earning by Sharing in the Smart City (Nov 22th)
7. …
8. …
(*) Funded by Swedish Internet Fund.

69. © Waher Data AB, 2018.
Smart City Labs*
1. Sensors and actuators (Oct 10th)
2. Connect and chat with your device (Oct 17th)
3. Publishing data from your sensor (Oct 24th)
4. Publishing and discovering devices (Nov 7th)
5. Controlling actuators (Nov 14th)
6. Decision Support for your devices (Nov 21th)
7. …
8. …
(*) Funded by Swedish Internet Fund.

70. © Waher Data AB, 2018.
 Raspberry Pi & Arduino
 Sensors, Actuators, Controllers,
Concentrators, Bridges
 Protocols:
MQTT, HTTP, CoAP, LWM2M, XMPP
 Interoperability
 Social Interaction
 Decision Support
 Product Lifecycle
 IoT Service Platforms
 IoT Harmonization
 Security
 Privacy
Amazon
Packt
Microsoft Store
Contact: https://waher.se/, https://littlesister.se/
Mastering Internet of Things

71. © Waher Data AB, 2018.
13. Open Discussion
?