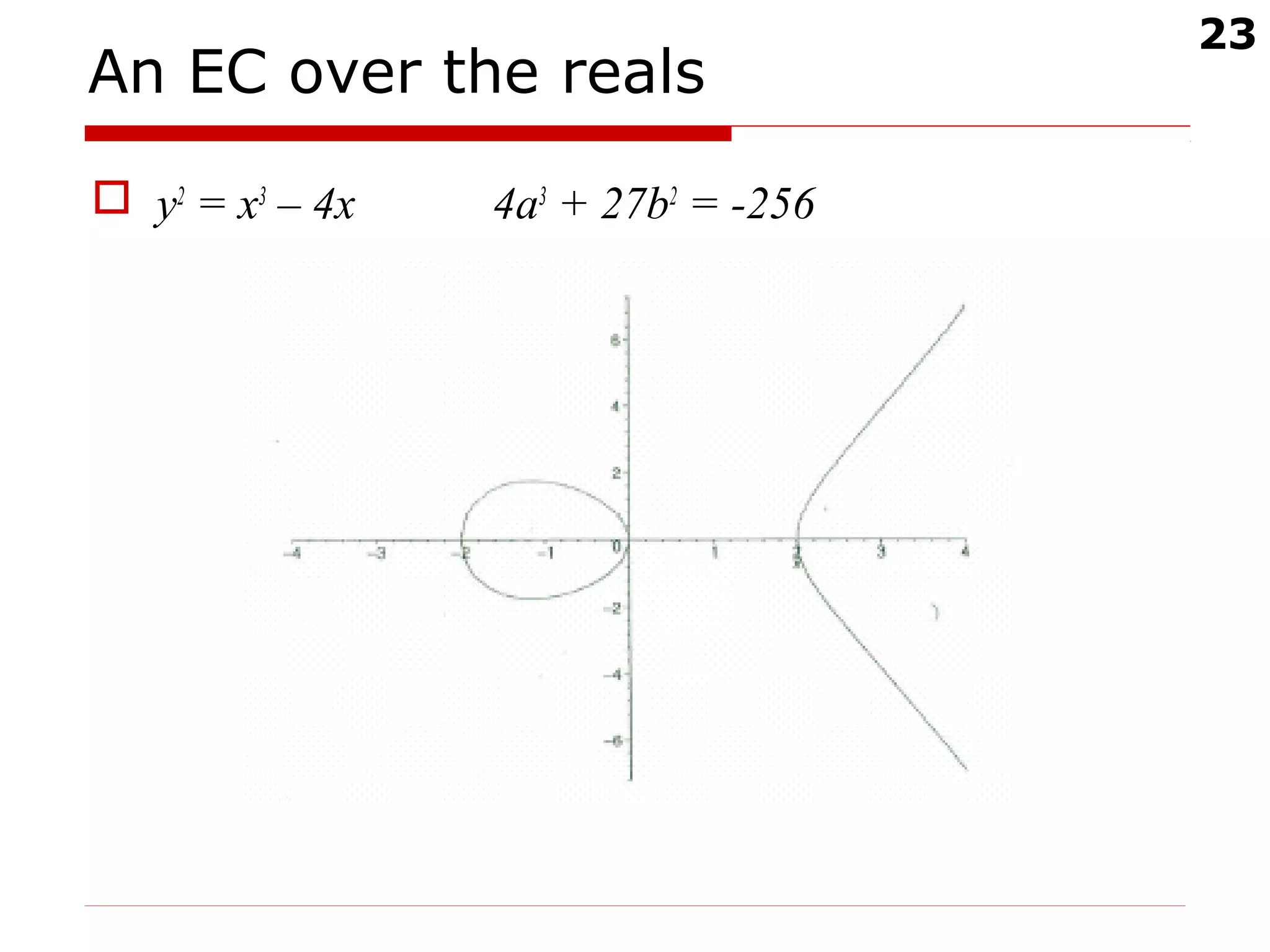
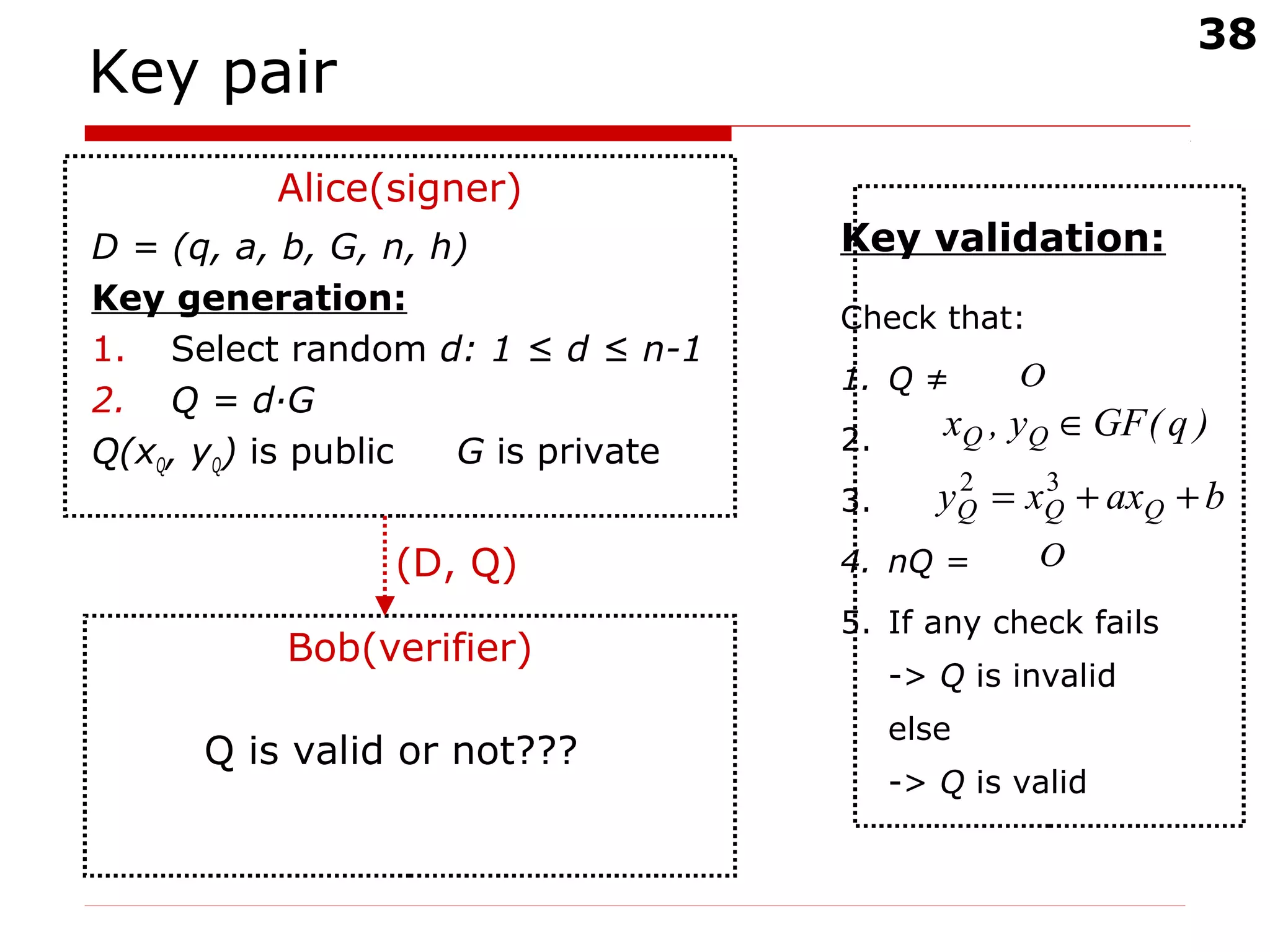
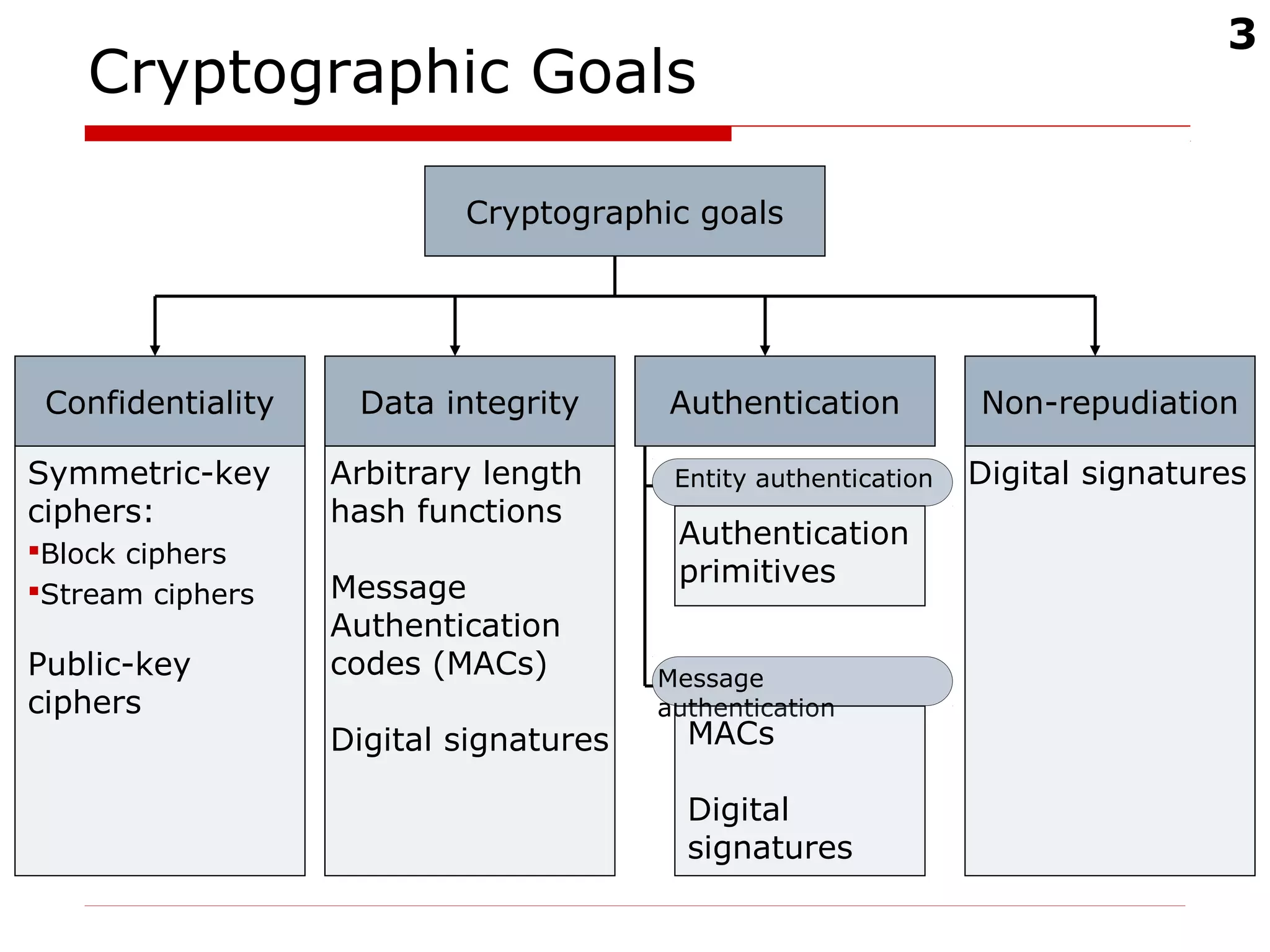
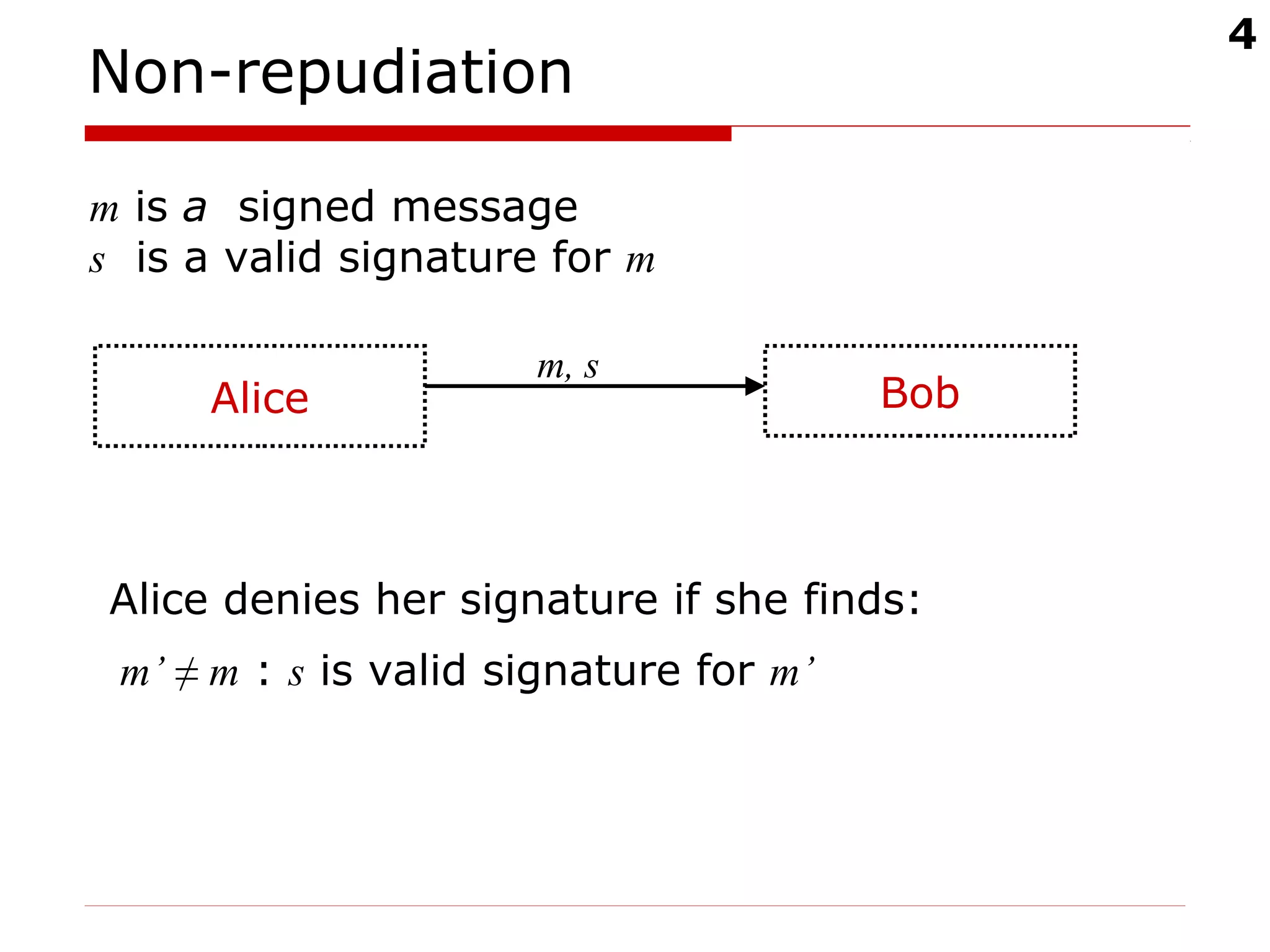
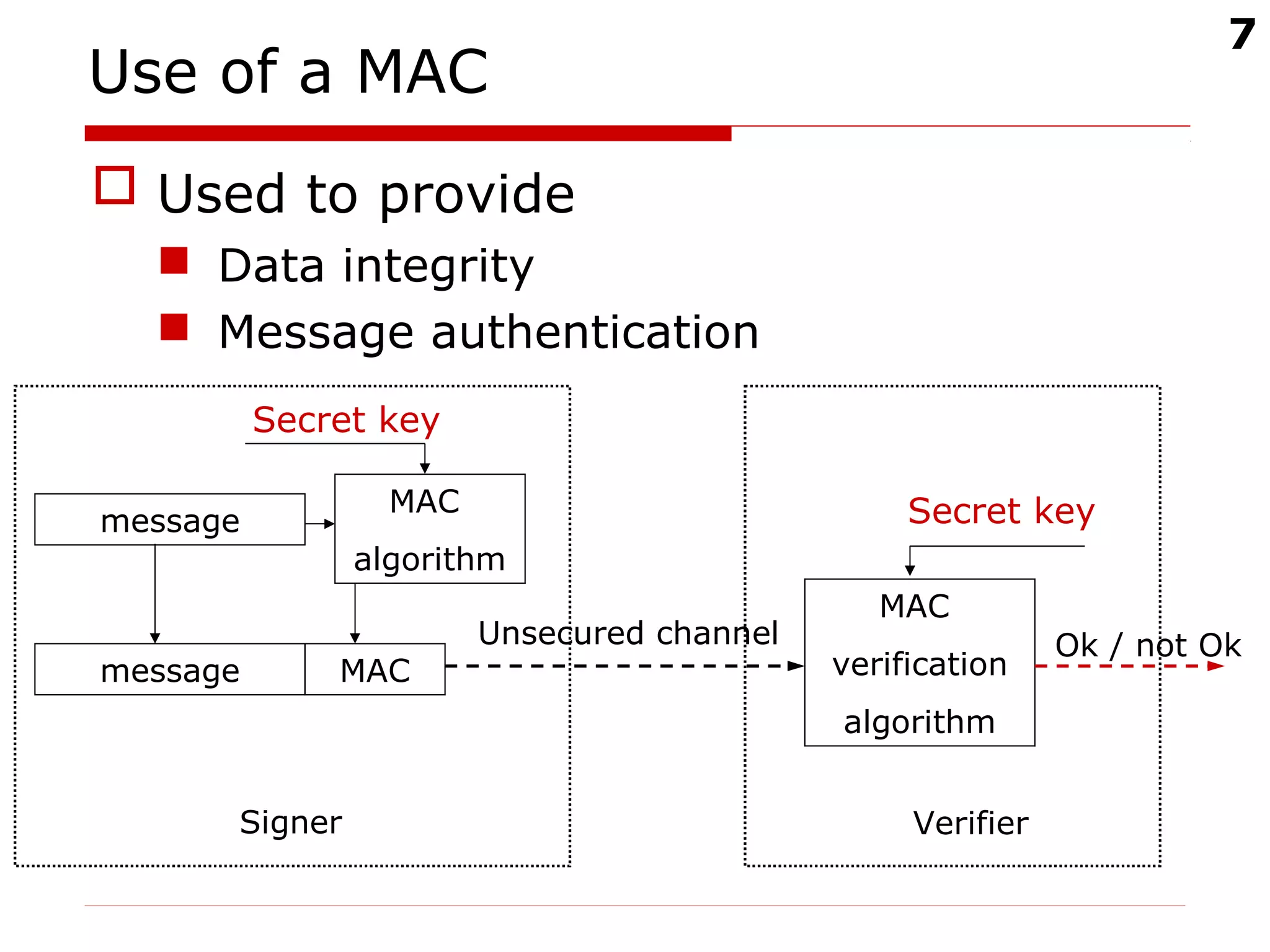
The document discusses digital signatures and message authentication codes (MACs), focusing on their cryptographic goals such as data integrity and non-repudiation. It explains the RSA digital signature algorithm and the Elliptic Curve Digital Signature Algorithm (ECDSA), including their key generation, signing, and verification processes. Additionally, it highlights the differences between MACs and digital signatures, emphasizing the performance characteristics and potential attacks on RSA signatures.

1. Digital Signatures
Presented by
signyourdoc

2. 2
Outline
 Cryptographic goals
 Message Authentication Codes (MACs)
 Digital signatures
 RSA digital signature
 Elliptic curve digital signature
 Comparison of ECDSA and RSA
signature

3. 3
Symmetric-key
ciphers:
Block ciphers
Stream ciphers
Public-key
ciphers
Cryptographic Goals
Cryptographic goals
Confidentiality Data integrity Authentication Non-repudiation
Message
authentication
Entity authenticationArbitrary length
hash functions
Message
Authentication
codes (MACs)
Digital signatures
Authentication
primitives
Digital signatures
MACs
Digital
signatures

4. 4
Non-repudiation
Alice Bob
m is a signed message
s is a valid signature for m
m, s
Alice denies her signature if she finds:
m’ ≠ m : s is valid signature for m’

5. 5
Message Authentication Codes
 MAC f(x, key):{0,1}* → {0,1}n
 knowing x and key f is easy to compute
 it is infeasible to calculate f(x, key)
without the key
 MAC are often block cipher based
 message m, secret key k
 specification of block cipher E
 MAC (m) = E( m, key )
 MAC (m) = E(hash(m), key )

6. 6
CBC-based MAC algorithm
E
key
0
X1(n bit)
E
key
X2 (n bit)
h1
…
h2
E
key
Xt (n bit)
ht-1
H = MAC
Optional
output transformationh1 = Ekey(x1)
hi = Ekey(hi-1 xi ), 2 ≤ i ≤ t
Algorithm CBC-MAC
INPUT: data x; specification of block cipher E; secret MAC key for E
OUTPUT: n-bit MAC on x
n bit
n bit
h1(n bit) h2(n bit)

7. 7
Use of a MAC
message
MAC
algorithm
message MAC
Secret key
Unsecured channel
Signer
MAC
verification
algorithm
Secret key
Verifier
Ok / not Ok
 Used to provide
 Data integrity
 Message authentication

8. 8
Digital Signatures Scheme
 Used to provide
 Data integrity
 Message authentication
 Non-repudiation
message
Signing
algorithm
message signature
Signer’s private key
Unsecured channel
Signer
Signature
verification
algorithm
Signer’s public key
Verifier
Ok / not Ok

9. 9
Difference between MAC and digital signature
 To prove the validity of a MAC to a third party,
you need to reveal the key
 If you can verify a MAC, you can also create it
 MAC does not allow a distinction to be made
between the parties sharing the key
 Computing a MAC is (usually) much faster than
computing a digital signature
 Important for devices with low computing power

10. 10
RSA signature algorithm

11. 11
RSA
 Developed in 1978 by Rivest, Shamir and
Adleman (RSA)
 Most popular public key cryptosystem
 Based on the hard problem of “integer
factorization”

12. 12
Key-Generation for RSA(1)
1. Generate two large random distinct primes
p and q, each roughly the same size
2. Compute n = pq and
3. Select random integer e:
4. Compute unique integer d:
5. Public key is (n, e); Private key is d
( ) ( 1)( 1)n p qφ = − −
1 , such that gcd( , ) 1e eφ φ< < =
1 , such that 1modd edφ φ< < =

13. 13
Key-Generation for RSA(2)
 Usually numbers with the right bit length are
chosen randomly and tested for primality
 Statistical tests are used to determine the
probability that these numbers are primes
i.e. Strassen – Test
Miller – Rabin – Test
 There is always an insignificantly low chance
that number is not prime

14. 14
Used notation
 M is a set of elements, called the
message space = Zn
 MS is a set of elements, called the
signing space = Zn
 R is a 1 to 1 mapping from M to MS,
called the redundancy function
 MR is the image of R: {y| y = R(x), xЄ M}
 R-1
is the inverse of R: MR M

15. 15
RSA signature generation and verification
 To sign a message A should:
 Compute:
where R(m) is a redundancy function
 Compute:
 A’s signature for m is s
 To verify A’s signature and recover m, B should:
 Obtain A’s authentic public key (n, e)
 Compute:
 Verify that ; if not, reject the signature
 Recover
]n,[),m(Rm~ 10 −= rangetheinintegeran
nmodm~s d
=
nmodsm~ e
=
RMm~ ∈
)m~(Rm 1−
=
Mm∈

16. 16
Proof that signature verification
works
 Euler’s theorem: ,
where is the Euler’s function of n
 If s is a signature for m, then:
 Since , then:
 Finally:
)m(Rm~,nm~s d
== mod
))n((ed,pqn φmod1≡=
)n(m~m~m~
m~m~m~s
q)n(
q)n())n((ede
mod
mod
≡⋅≡
≡≡≡≡
⋅
+⋅
ϕ
ϕϕ 11
m))m(R(R)m~(R == −− 11
11 =≡ )n,agcd(,na )n(
modϕ
)n(ϕ

17. 17
RSA signature example
Alice
 p=5 q=7 n = 35 φ(n) = 4·6=24
 e = 5; d: ed = 5d=1 mod 24 => d = 5
Public key: (n=35, e=5) Private key: d=5
 M = [0, n-1]
 For all m Є M R(m)=m
 m = 26; R(m) = 26 s = 265
mod 35 = 31
Bob:
 R(m) = 315
mod 35 = 26 Є [0, n-1]
 m = R-1
(m) = 26
=m~
=m~

18. 18
Possible Attacks on RSA signature
 Integer factorization
 If an adversary is able to factor n, then
 Multiplicative property of RSA
 If , then s is valid signature for m:
 Hence, to avoid this attack R must not be
multiplicative, i.e.
))n((ed:d)q)(p()n(,pqn φφ modfindand 111 ≡−−==
)n(ss)m~m~(m~sm~m~m~
)n(modm~s
)n(modm~s dd
d
d
modthenif 212121
22
11
====⇒
=
=
RMm~ ∈ )m(Rm~ =
)b(R)a(R)ba(RMb,a ⋅≠⋅∈∀

19. 19
Performance characteristics
 n=pq , where n is 2k-bit, p&q – k-bit primes
 takes bit operations
 Verification is significantly faster that signing if
e is chosen to be a small number, e.g.
 It is not recommended to restrict the size of d
nms d
mod= )k(O 3
111
123 16
=−−
+==
))q)(p(,egcd(qp
,e,e
thatsochosenbemustand
or

20. 20
 n=pq , where n is 2k-bits, p&q – k-bits primes
 ISO/IEC 9796
R:
 To sign a kt-bits message m:
 Divide m = m1|| m2|| m3||… || mt and sign each block
individually one transmits 2kt bits.
 Sign a l-bits hash(m), l ≤ k. Then one transmits
kt+2k bits. (kt – to transmit the message)
 If t > 2, then kt+2k < 2kt
2k bits
m~
Short vs. long messages
⇒
m
k bits

21. 21
The Elliptic Curve Digital Signature
Algorithm (ECDSA)

22. 22
Elliptic curves (EC) over the reals
 A non-singular EC is the set E of solutions
to the equation
together with a special point O, where
 has three
distinct roots
RR)y,x( ×∈
baxxy ++= 32
0274 23
≠+∈ ba,Rb,a
00274 323
=++⇔≠+ baxxba

23. 23
An EC over the reals
 y2
= x3
– 4x 4a3
+ 27b2
= -256

24. 24
Addition – Geometric Approach
 Chord-and-tangent
rule P + Q = R, P ≠ Q
 Point doubling
P + P = 2 P = R
x
y
(x1, y1) = P
Q = (x2, y2)
R = (x3, y3)
x
y
P = (x1, y1)
R = (x3, y3)
-R = (x3, -y3)
-R = (x3, -y3)
Ο

25. 25
Addition – Algebraic Approach
E is elliptic curve over the reals
1. ( is the identity element )
2. If
3.
4.
Ο=−+∈= )y,x()y,x(,E)y,x(P then
PPPEP =+=+∈∀ ΟΟ
whereThen
andLet
),y,x(QP
.QP,E)y,x(Q,E)y,x(P
33
2211
=+
±≠∈=∈=
( ) 21
2
3 12
12
xxx xx
yy
−−= −
−
( )( ) 1313 12
12
yxxy xx
yy
−−= −
−
where2ThenLet ),y,x(P.PP,E)y,x(P 3311 =−≠∈=
1
2
2
3
3 2
1
2
1
xx y
ax
−




=
+
( ) 1312
3
3 1
2
1
yxxy y
ax
−−




=
+
-P
Ο

26. 26
Galois Fields (Finite Fields) GF (q)
 Is a set of elements (G, + , *)
that satisfy certain arithmetic properties
 Finite Field exists iff q is a prime power
 If q = p, p is prime
 {0, 1, ... , p - 1 } are the field elements
 ADDITION:
 MULTIPLICATION:
 INVERSION:
prbaqba mod),GF(, ≡+∈
prbaqba mod),GF(, ≡⋅∈
paaaa mod1:0 11
=⋅∃≠∀ −−

27. 27
Elliptic Curves Over Finite Fields
Over GF(p), p is prime, p > 3
 Elliptic curve E equation
where
 E consists of
 all pairs
satisfying curve equation
 special point - point at infinity
baxxy ++= 32
)p(modba),p(b,a 0274 23
≡/+∈ andGF
)p(y),p(x),y,x( GFGF ∈∈
),( 00=Ο

28. 28
Example 1: elliptic curve over GF(23)
 p = 23
 The points in E are and the following:
(0, 2) (0, 21) (1, 11) (1, 12) (4, 7) (4, 16)
(7, 3) (7, 20) (8, 8) (8, 15) (9, 11) (9, 12)
…
28 points + = 29 points
 Let’s consider (4, 7)
64 + 4 + 4 = 72 = 3 (mod 23) 49 = 3 (mod 23)
2322274
414
23
32
mod=+
==++=
ba
b,a,xxy:E
Ο
),( 00Ο

29. 29
Basic Facts
Let E(GF(q)) be an EC over GF(q)
 The points of E(GF(q)), form a group under
addition
 Hasse’s theorem:
Number of points on E (group order):
 If #E is prime then the group is cyclic and
 If #E has a prime factor, that there exists a
cyclic subgroup
qt,tq))q(GF(E 21 ≤−+=#
Ο
{ }#Ek:kP))q(GF(E:))q(GF(EP ≤≤=∈∃ 0

30. 30
Example 2: elliptic curve over GF(23)
 p = 23

 The points in E are and the following:
P = (0, 2) 2P = (13, 12) 3P = (11, 9) 4P = (1, 12)
5P = (7, 20) 6P = (9, 11) 7P = (15, 9) 8P = (14, 5)
9P = (4, 7) 10P = (22, 5) 11P = (10, 5) 12P = (17, 9)
13P = (8, 15) 14P = (18, 9) 15P = (18, 14) 16P = (8, 8)
17P = (17, 14) 18P = (10, 18) 19P = (22, 18) 20P = (4, 16)
21P = (14, 18) 22P = (15, 17) 23P = (9, 12) 24P = (7, 3)
25P = (1, 11) 26P = (11, 14) 27P = (13, 11) 28P = (0, 21)
29P = O 30P = P
29 points
cyclicisgroup# ⇒=
++==
29
429 32
E
xxy:E
Ο

31. 31
ECDSA parameters setup
 Create (random) public abstract groups
 Domain Parameter Generate: Complex &
public. DP often taken from published list.
 Domain Parameter Validate:
Easy & public
 Key Pair Generate: Easy & private.
 Key Pair Validate: Easy & public.

32. 32
ECDSA Domain Parameters
 Domain parameters D = (q, a, b, G, n, h)
 Field size q, q = p or q = 2m
 Coefficients a, b in GF(q) of E=Ea,b
(GF(q)):
 Seed s of length ≥ 160 bits (Optional)
 Base point G=(xG, yG) on curve E, i.e.
 Order n of G: n is prime,
 Cofactor h: #E(GF(q)) = hn
qnn 4and2160
>>
0274 23
≠+ ba
)q(GFy,x GG ∈

33. 33
Curve parameters generation(1)
 Input: GF(p), p is prime
 Output: seed, curve coefficients a & b
 Used notations: stv,
p
s ⋅−=




 −
= 160
160
12log
Hash
algorithm
g > 160 bits
Ν∈z
W0
v-1 bits
Arbitrary SEED
160 bits
Wstringbit
hash(z + 1) hash(z + 2) … hash(z + s)
(v-1)+ s·160 < log2 p bits
W0

34. 34
Curve parameters generation(2)
1.
2. if abort and start again
3. Choose a,b
4. Result: y2
= x3
+ ax + b
 if
 Exclude singular curves
Ν∈→ rW



≡+
=
pr
r
mod0274
0
pabrb,a)p( mod:GF 32
00 ≡⋅≠≠∈





−=
==
⇒≡+
p
b
a
ba
pba
mod
and
EC)(singularmod
4
27
00
0274
2
323

35. 35
Isomorphism classes of ECs(1)
 E1: y2
=x3
+a1x +b1 and E2: y2
=x3
+a2x +b2
are isomorphic
 Step 3: Choose a,b
 There only 2 variants for a and b on step 3
2
2
3
2
2
1
3
1
2
6
12
4
10
b
a
b
a
.e.i,bubauau),p(u ===≠∈∃ and:GF
⇔
pmodabrb,a)p(b,a 32
00 ≡⋅≠≠∈ :GF

36. 36
Isomorphism classes of ECs(2)
 Let’s prove that there are precisely 2 choices for
(a, b) on step 3 :
 We can find a1, b1 and a2, b2:
 We can not find a3, b3 : E3 is not isomorphic to E1 orE2
isomorphicnotarecurvesandpmodr
b
a
b
a
pmodku:k
pmodbub
pmodaua
==⇒
≡∃/
=
=
2
2
3
2
2
1
3
1
2
1
3
2
1
2
2
( ) 2
1
toisomoprhici.e.Else
toisomoprhici.e.
If
sLet'
sLet'
E,pmodaa
pmodaua
pmodaua
E
,pmodblbub,pmodalauapmodul:l
pmodbub,pmodauapmodu
b
b
a
a
:u
pmodr
b
a
b
a
b
a
u
u
2
2
3
1
2
2
1
2
33
1
6
1
3
331
4
1
2
333
2
1
3
331
2
33
6
32
1
2
3
3
1
3
3
3
2
3
3
3
2
2
3
2
2
1
3
1
3
=⇒
=
=
====⇒≡∃
==⇒==∃
===

37. 37
Domain Parameter Generation
 Domain parameters D = (q, a, b, G, n, h)
1. Generate EC coeffs a & b
E ( GF(q) ): y2
= x3
+ ax + b
2. Compute #E( GF(q) ) (e.g. Schoof’s algorithm)
3. Verify that , n is prime,
4. if not, go to step 1
5. Verify that if not, go to step 1
6. Verify that n≠q if not, go to step 1
7. Select an arbitrary point
Set
Repeat until
nhE =# qnn 4and2160
>>
2011 ≤≤−/ k,q|n k
)).q((E'G GF∈
'.G)n/N(G ⋅=
Ο≠G

38. 38
Alice(signer)
Key pair
D = (q, a, b, G, n, h)
Key generation:
1. Select random d: 1 ≤ d ≤ n-1
2. Q = d·G
Q(xQ, yQ) is public G is private
Bob(verifier)
(D, Q)
Q is valid or not???
Key validation:
Check that:
1. Q ≠
2.
3.
4. nQ =
5. If any check fails
-> Q is invalid
else
-> Q is valid
Ο
)q(GFy,x QQ ∈
Ο
baxxy QQQ ++= 32

39. 39
Bob
Parameters D = (q, a, b, G, n, h)
Alice’s public key Q
Alice’s signature (r, s) on m
To sign message m:
1. k randomly chosen 0 < k < n-1
2. k·G = (x1, y1) r =x1 mod n
3. if r = 0 abort and start again
4. e = SHA-1(m)
5. s = k-1
· ( e + d·r) mod n
6. if s = 0 abort and start again
Output: (r, s)
ECDSA generation & verification
( ) ( )
rvkGG)duu(QuGu
nduuwrdwerdsesdreskndreks
=⇒=+=+
+≡+≡+≡+≡⇔+= −−−−
2121
21
1111
modmod
acceptif →= rv
Alice
Parameters D = (q, a, b, G, n, h)
Associated keys (d, Q)
Proof that signature verification works:
To verify signature (r, s):
1. check: 1 ≤ r ≤ n-1, 1 ≤ s ≤ n -1
2. e = SHA-1(m)
3. w = s-1
mod n
4. u1 = e·w mod n u2 = r·w mod n
5. X = u1·G + u2·Q, if
6. X=(x1, y1) v = x1 mod n
7.
reject→=ΟX
D, Q, m, r, s

40. 40
Ordinary DLP
 Definition:
Given: prime p,
generator g of GF(p),
non zero element y‑ ∈ GF(p),
Find: the unique integer k, 0 ≤ k ≤ p – 2:
y ≡ gk
(mod p)
k is called the discrete logarithm of y to the base g
 Known attacks
The most efficient:
Index Calculus Method O( )
ppo
e
lnlnln))1(2/1( +

41. 41
Elliptic Curve DLP
 Identified in 1985 – Koblitz and Miller suggested
using it in place of DLP
 Definition:
Given: EC E defined over GF(q),
point P∈E( F(q) ) of order n,
point Q∈E( GF(q) ),
Determine: the integer l, 0 ≤ l ≤ n – 1: Q = lP
 Arises in groups defined on EC
 Hard Problem
 Only exponential algorithms known

42. 42
Known Attacks on ECDLP
 Pollard’s Rho Algorithm O( )
 Parallelized Pollard’s Rho O( )
r is the number of processors used
Precautions:
 Pohlig-Hellman Algorithm O( )
Precautions:
 Menezez-Okamoto-Vanstone (MOV) O( )
Precautions:
 No index calculus method found
n
r/n
q
)log(qk ⋅
160
2>n
primeisn
2011 ≤≤−/ k,q|n k

43. 43
Pollard’s Rho Algorithm(1)
To find k where Q=kP, and n is the group
order:
 Use a pseudo-random walk through the group
 Start at a known point
 When a collision occurs, we can find k
 Because there is not enough room to store all
visited points, we only store distinguished points
(points with some distinguishing property, such
as the first i lower order bits equal to zero).

44. 44
Pollard’s Rho Algorithm(2)
 The random walk is defined as:
 Where the Si are three sets of points (e.g. Si may be
points such that x mod 3 ≡ i), and the ri are
randomly chosen.





∈++
∈++
∈++
=+
365
243
121
1
SRQrPrR
SRQrPrR
SR,QrPrR
R
ii
ii
ii
i
for
for
for

45. 45
Pollard’s Rho Algorithm(3)
 R0 is chosen to be a known multiple of P and Q.
 For each iteration, Ri+1 is found, and also what
multiple of P and Q it is.
 When a collision occurs, we have:
P
db
ac
Q
dQcPbQaP
RR ji




−
−
=
+=+
=

46. 46
Pollard’s Rho Algorithm(4)
 The number of iterations is
 With this approach, the path of the pseudo-random
walk depends on Q.
 There is no precomputation.
 Calculations from previous ECDLP’s are of limited
usefulness in subsequent ECDLP’s, because collisions
are only detected for distinguished points.
( )nO

47. 47
Duplicate-Signature Key Selection
 An adversary
 Selects arbitrary c:
 Computes:
 Forms:



≠+=
−≤≤
−−
0
11
11
)nmod)rcses((t
nc
:
( ))rQeG(GX)nmodt(G
)m(SHAerQseGsX
rce +==
−=+=
+
−
−−
11
11
1 )where(
GcQ)h,n,G,b,a,FR,q(D EE == and
Alice Bob
Adversary E
D, Q, m, r, s
DE, QE, m, r, s
Proof of work:
kGG)wrdwe(wrdGweGwrQweGw)rce(
)rwcew()cuu(GcuGuQuGuX
rce
rQeG
rce
rQeG
rce
rQeG
E
=+=+=+=⋅+⋅=
=+⋅=+⋅=+=+=
+
+
+
+
+
+
212121

48. 48
Key Size Comparisons
Sym. key: 80, 112, 128, 192, 256
ECC n: 161, 224, 256, 384, 512
RSA n: 1024, 2048, 3072, 7680, 15360

49. 49
ECDSA Advantages
 Elliptic curves offer a much shorter key length
than RSA.
 There are some environments where 1024-bit
RSA can not be implemented, while 163-bit
ECC can.
 No subexponential-time algorithm is known for
the EC discrete logarithm problem.

50. 50
Discussion
???

51. 51
Exercises(1)
 Does this equation define an EC over GF(17)?
y2
= x3
+ 10x + 5
 Do the points P(2,0) and Q(6,3) lie on the
elliptic curve y2
= x3
+ x + 7 over GF(17)?
 What are the negatives of the following elliptic
curve points over GF(17)?
P(5,8) Q(3,0) R(0,6)
 In the elliptic curve group defined by
y2
= x3
+ x + 7 over GF(17), what is P + Q
if P = (2,0) and Q = (1,3)?

52. 52
Exercises(2)
 Suppose that p > 3 is an odd prime
a, b Є GF(p)
 Further suppose that
has 3 distinct roots in GF(p)
 Prove that the corresponding elliptic curve
E is not cyclic
pbaxx mod03
≡++

53. 53
References
 Don Johnson, Alfred Menezes, The Elliptic
Curve Digital Signature, February 2000
http://www.cacr.math.uwaterloo.ca
 A. Menezes, P. van Oorschot, S. Vanstone,
Handbook of Applied cryptography, CRC Press
1996
http://www.cacr.math.uwaterloo.ca/hac
 Douglas R. Stinson Cryptography, Theory and
Practice, CRC Press

54. 54
Elliptic Curves Over Finite Fields
Over GF(2m
)
 Elliptic curve E equation
where
 E consists of
 all pairs
satisfying curve equation
 special point - point at infinity
baxxxyy ++=+ 232
02 ≠∈ b),(GFb,a m
and
)(GFy),(GFx),y,x( mm
22 ∈∈
Ο

55. 55
Example 2: elliptic curve over GF(24
)
 Generator polynomial f(x) = x4
+ x + 1

 The points in E are and the following:
15 points + = 16 points
042432
1 ααα ==++=+ b,a,xxxyy:E
Ο
Ο
)()()(
)()()()(
)()()()(
)()()()(
121212810
10139109146
8611535133
83136
0
1110
ααααα
αααααααα
αααααααα
αααα
,,,
,,,,
,,,,
,,,,

56. 56
Addition – Algebraic Approach
E – elliptic curve over GF(2m
)
1.
2. If
3.
4.
Ο=++∈= )yx,x()y,x(,E)y,x(P then
PPPEP =+=+∈∀ ΟΟ
whereThen
andLet
),y,x(QP
.QP,E)y,x(Q,E)y,x(P
33
2211
=+
±≠∈=∈=
( ) axxx xx
yy
xx
yy
++++= +
+
+
+
21
2
3 21
21
21
21
( ) ( ) 13313 21
21
yxxxy xx
yy
+++⋅= +
+
where2ThenLet ),y,x(P.PP,E)y,x(P 3311 =−≠∈=
2
1
2
13 x
b
xx += ( ) 331
2
13 1
1
xxxxy x
y
+++=
-P

57. 57
Curve parameters generation
 Used notations:
 Input: prime p
 Output: seed, curve coefficients a & b
 Algorithm:
1. Choose a bit string seedE: g = |seedE| ≥ 160 bits
2. H = SHA-1(seedE)
3. z = (int) seedE
4. For i from 1 to s do:
 si = (z+i) mod 2g
 Wi = SHA-1 (si)
1.
2. r= (int) W, if r = 0 or 4r + 27 ( 0 mod p ) go to step 1
3. Choose a,b
4. The elliptic curve is: y2
= x3
+ ax + b
5. Output (seedE, a, b)
≡
  ( )  stv,/ts,plogt ⋅−=−== 16016012
H
160 bits
W0
v-1 bits
W0 W1
… WsW =
pmodabrb,a)p(GF 32
00 ≡⋅≠≠∈ :

58. 58
Alice domain
D = (q, FR, a, b, G, n, h)
D is valid or not?
D validation:
Check that:
1.
2.
3.
4.
5. n is prime AND n > 2160
6. #E ≠ q
7.
8.
9.
10. If any check fails
-> D is invalid
else
-> D is valid
m
qorpq 2==
Domain Parameters Validation
2011 ≤≤−/ k,q|n k
)|n(qn E#/> 2
4
Bob domain
D
0274 23
≠+ ba
Ο≠G
Ο=nG
  'hhn/)q('h =+= ,2
1

59. 59
Verifying the order of an EC
 Hasses’s theorem:
 Hence, check implies that
 Also since:
 Hence if:
22
1121 )q(E)q(qt,tqE +≤≤−⇔≤−+= ##
qn 4>
22
16 nEqn /⇒> #





 +
=++≤≤−+∃
n
)q(
h,qqnhqq:h
2
1
2121!
⇒=−−+ q)q()q( 411 22
nhE
n
)q(
hqn,nG
toequalindeedis#
and ⇒




 +
=>=
2
1
4Ο

60. 60
Potential CA Services
 POP - Proof of possession of private key.
Can use zero-knowledge proof.
 PKV - Public Key Validation
shows public key makes arithmetic sense.
 POP and PKV can be considered duals of
each other. Doing both provides strong
assurance.

61. 61
Security Considerations
 Per-message secret k:

 Repeated usage of k:
 Check: 1 ≤ r ≤ n-1, 1 ≤ s ≤ n -1


)m(SHAs,r),b,(G 100 −===
0001
01 2
1
1
==⇒==+⋅=
==⋅= −
rv)b,(X,GGX
u,eeu
i.e.
nmod)eks(rdnmod)dre(ks −=⇔+= −− 11
nmod)ee()ss(k
nmodee)ss(k
nmoddreks
nmoddreks
nmod)dre(ks
nmod)dre(ks
21
1
21
2121
22
11
2
1
2
1
1
1
−−≡
−≡−
+≡
+≡
⇔
+≡
+≡
−
−
−
To verify signature (r, s):
1. check: 1 ≤ r ≤ n-1, 1 ≤ s ≤ n -1
2. e = SHA-1(m)
3. w = s-1 mod n
4. u1 = e·w mod n u2 = r·w mod n
5. X = u1·G + u2·Q, if
6. X(x1, y1) v = x1 mod n
7.
reject→=ΟX
acceptif →= rv

62. 62
Attacks on Hash function
 SHA-1
 Preimage resistance hard to find x: H(x) = y
 Collision resistance hard to find x1 and x2 : H(x1) = H(x2)
 If not preimage resistant
 One can forge signature:
Calculate parameters r, s, e, m : e = SHA-1(m),
where (r, s) is valid signature for m
 If not collision resistant
 One can repudiate messages:
Generate m’: SHA-1(m) = SHA-1(m’)

63. 63
Signature Forgery
 Signature Forgery
 A forgery is a signature computed without
the signer’s private key
 selective forgery: an adversary is able to
create a valid signature for a particular message
chosen a priori
 existential forgery – an adversary is able to
forge a signature for at least one message