The document discusses attribute-based encryption (ABE) schemes, including Key-Policy ABE (KP-ABE) and Ciphertext-Policy ABE (CP-ABE). It defines the components of KP-ABE and CP-ABE, including setup, encryption, key generation, and decryption algorithms. It also describes the security models and proves the selective security of the GPSW KP-ABE scheme and correctness of the Waters CP-ABE scheme under the decisional bilinear Diffie-Hellman assumption. The document outlines the KP-ABE and CP-ABE constructions and security proofs in detail.

1. 1/30
CPDA Lecture 12 Attribute-Based Encryption
曾一凡
林彥賓
2020 年 8 月 12 日
2020 年 8 月 12 日

2. 2/30
Outline
Introduction
KP-ABE
Definition
Security Model
Access Tree To LSSS
Scheme
Correctness
Security Proof
CP-ABE
Definition
Security Model
Waters Scheme
Correctness
Security Proof
2020 年 8 月 12 日

3. 3/30
Introduction
Key-Policy Attribute-Based Encryption (KP-ABE): an attribute set is
associated with a ciphertext, and an access structure(Policy) is
associated with private key
Ciphertext-Policy Attribute-Based Encryption (CP-ABE): a user’s
private key is associated with a set of descriptive attributes, and a
ciphertext is associated with an access structure(Policy)
2020 年 8 月 12 日

4. 4/30
KP-ABE Definition
Setup(1λ): Taking as input the security parameter, the algorithm
outputs the system parameter params and the master secret key msk
Encrypt(S, M): Taking as inputs a set of attributes S and a message
M, the algorithm outputs a ciphertext CT
KeyGen(msk, A): Taking as inputs the master secret key msk and an
access structure A, the algorithm outputs a private key D
Decrypt(CT, D): Taking as inputs a ciphertext CT and a private key
D, the algorithm outputs a message
define |=
S |= A denote “S satisfies A”
correctness
For CT ←− Encrypt(S, M), D ←− KeyGen(msk, A), we have
M ←− Decrypt(CT, D) if S satisfies A
2020 年 8 月 12 日

5. 5/30
KP-ABE Security Model
Setup: The challenger C runs the Setup algorithm and sends params
to the adversary A
Phase 1: The adversary A makes polynomially many queries to the
following oracles
KeyGen(Ai): Upon inputting an access structure Ai, the oracle returns
the corresponding private key DAi
Decrypt(CT, Ai): Upon inputting a ciphertext CT and an access
structure Ai, the oracle returns the output of Decrypt(CT, DAi
)
Challenge: The adversary A submits two distinct message (M0, M1)
of the same length, and a target attribute set S∗, where S∗ does not
satisfy the access structures queried in Phase 1. Then the challenger
C chooses a bit b ←− {0, 1}, and returns CT ←− Encrypt(S∗, Mb)
Phase 2: It is the same as Phase 1 except Decrypt(CT∗, Aj) and
KeyGen(Aj) such that S∗ |= Aj are not allowed
2020 年 8 月 12 日

6. 6/30
KP-ABE Security Model
Guess: The adversary A outputs a bit b, and wins the game if b = b.
The advantage of the adversary A in winning the game is defined as
Adv(A) = Pr[b = b]−1/2
We say that an ABE scheme is CCA secure if for all PPT adversary
A, Adv(A) is negligible
2020 年 8 月 12 日

7. 7/30
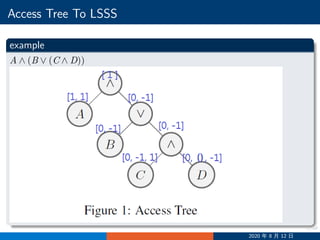
Access Tree To LSSS
1 label the root with [1] and label each node from the root to leaves
2 If an internal node is “∧”labelled with a vector v, then we label its left
son with [v, 1], and the right son with [0, ..., 0, −1]. The sum of left
and right should be [v, 0]
3 If an internal node is “∨”then we label the two sons with the same
vector as their parent
4 pad 0 to the shorter vectors to make all the vectors the same length
2020 年 8 月 12 日

8. 8/30
Access Tree To LSSS
example
A ∧ (B ∨ (C ∧ D))
2020 年 8 月 12 日

9. 9/30
KP-ABE Scheme
Setup(1λ): Define the universe U = {1, 2, ..., k}
1 Randomly choose ti ←− Zp, i = 1, 2, ..., k
2 Compute Ti = gti
, i = 1, 2, ..., k
3 Randomly choose y ←− Zp and compute Y = e(g, g)y
4 Set params = (T1, T2, ..., Tk, Y), msk = (t1, t2, ..., tk, y)
5 Output (params, msk)
Encrypt(S, M): To encrypt a message M ∈ GT for an attribute set
S ∈ U
1 Randomly choose s ←− Zp
2 Compute C = MYs
3 For x ∈ S, compute Cx = Ts
x
4 Output CT = (C, {Cx}x∈S)
KeyGen(msk, A): To generate the private key for access structure
A = (MZℓ×n
p , ρ)
1 Randomly choose v2, v3, ..., vn ←− Zp and set v = (y, v2, ..., vn)
2 Let Mi denote the i-th row of M. For i = 1 to ℓ, compute Di = g
Mi,v
tρ(i)
3 output private key D = ({Di}i=1,...,ℓ)
2020 年 8 月 12 日

10. 10/30
KP-ABE Scheme
Decrypt(CT, D): Assume that CT and D are associated with an
attribute set S and an access structure A = (M, ρ), respectively. Let
I ⊂ {1, ..., ℓ} be defined as I = {i : ρ(i) ∈ S} If S |= A, then by the
property of LSSS, there must exist a set of constant {wi}iI such that
i wiMi = (1, 0, ..., 0)
n
. Output
M =
C
i∈I e(Di, Cρ(i))wi
Since i∈I wiMi = (1, 0, ..., 0)
n
, we have that
i∈I
wi Mi, v =
i∈I
wiMi, v = (1, 0, ..., 0), (y, v2, ..., vn) = y
2020 年 8 月 12 日

11. 11/30
KP-ABE Correctness
i∈I
e(Di = g
Mi,v
tρ(i) , Cρ(i) = (T = gt
)s
ρ(i))wi
=
i∈I
e(g, g)wiMi,vs
= e(g, g)s
∏
i∈I wiMi,v
= e(g, g)sy
= Ys
(1)
C
i∈I e(Di, Cρ(i))wi
=
MYs
Ys
= M
2020 年 8 月 12 日

12. 12/30
KP-ABE Security Proof
Theorem
GPSW KP-ABE is selectively secure against the chosen-plaintext attacks
under the DBDH assumption
Given the instance (g, ga, gb, gc, Z = e(g, g)a,b,c) of the DBDH problem
Init: The adversary A submits a target attribute set S∗
Setup:The challenger C performs as follows.
1 Y = e(ga
, gb
), which means we implicitly set y = ab
2 For i ∈ S∗
, random choose fi ←− Zp and compute Ti = gfi
(thus ti = fi)
3 For i ∈ U/S∗
random choose hi and compute Ti = (gb
)hi
(thus
ti = bhi)
4 Return params = ({Ti}i∈U, Y)
2020 年 8 月 12 日

13. 13/30
KP-ABE Security Proof Phase 1 KeyGen Query
let l = (1, 0, ..., 0)
n
,
Ms be the submatrix whose rows correspond to the attribute in S∗
goal
find a vector v such that l · v = y = ab, and g
Mi,v
tρ(i) can be computed no
matter ρ(i) ∈ S∗ or not
Proposition 1
A vector x is independent of a set of vector represented by a matrix N, if
and only if there is a vector w such that N · w = 0 while x · w ̸= 0
Since S∗ does not satisfy A, the rows of MS∗ do not generate l, i.e., l is
independent of MS∗
2020 年 8 月 12 日

14. 14/30
KP-ABE Security Proof Phase 1 KeyGen Query
define
v = u + ψw, MS∗ · wT = 0 and l · wT = δ ̸= 0
random choose k = (k1, k2, ..., kn) and set u = bk = (bk1, bk2, ..., bkn)
l · vT
= ab
⇒ l · (u + ψw)T
= ab
⇒ bk1 + ψδ = ab
⇒ ψ = b(
a − k1
δ
)
2020 年 8 月 12 日

15. 15/30
KP-ABE Security Proof Phase 1 KeyGen Query
For ρ(j) ∈ S∗, tρ(j) = fρ(j)
Mj, v
tρ(j)
=
Mj, u +(ψ Mj, w = 0)
fρ(j)
= b(
Mj, y
fρ(j)
)
Di = (gb
)
Mj,y
fρ(j)
For ρ(j) /∈ S∗, tρ(j) = bhρ(j)
Mj, v
tρ(j)
=
Mj, (u = bk) +(ψ = b(a−k1
δ )) Mj, w
bhρ(j)
=
Mj, k +(a−k1
δ ) Mj, w
hρ(j)
=
δ Mj, k −ki Mj, w
δhρ(j)
+ a(
Mj, w
δhρ(j)
)
Di = g
δMj,k−kiMj,w
δhρ(j) · (ga
)
Mj,w
δhρ(j)
2020 年 8 月 12 日

16. 16/30
KP-ABE Security Proof
Challenge: A submits two messages M0, M1, and C performs as
follows
1 Randomly choose b ←− {0, 1} and compute C = MbZ
2 Compute C = Mbe(g, g)abc
= MbYc
3 For i ∈ S∗
, compute Tc
i = gfic
= (gc
)fi
4 Return CT∗
= (C, {Ci}i∈S∗ )
Phase 2: same as Phase 1
Guess: since C = Mbe(g, g)abc = MbYc the challenger is able to solve
the DBDH problem if there is an adversary wins the game with
non-negligible advantage
2020 年 8 月 12 日

17. 17/30
CP-ABE Definition
Setup(1λ): Taking as input the security parameter, the algorithm
outputs the system parameter params and the master secret key msk
Encrypt(A, M): Taking as inputs an access structure A and a
message M, the algorithm outputs a ciphertext CT
KeyGen(msk, S): Taking as inputs the master secret key msk and an
attribute set S, the algorithm outputs a private key D
Decrypt(CT, D): Taking as inputs a ciphertext CT and a private key
D, the algorithm outputs a message
correctness
For CT ←− Encrypt(A, M), D ←− KeyGen(msk, S), we have
M ←− Decrypt(CT, D) if S satisfies A
2020 年 8 月 12 日

18. 18/30
CP-ABE Security Model
Setup: The challenger C runs the Setup algorithm and sends params
to the adversary A
Phase 1: The adversary A makes polynomially many queries to the
following oracles
KeyGen(Si): Upon inputting an attribute set Si, the oracle returns the
corresponding private key DSi
Decrypt(CT, Si): Upon inputting a ciphertext CT and an attribute set
Si, the oracle returns the output of Decrypt(CT, DSi
)
Challenge: The adversary submits two distinct message (M0, M1) of
the same length, and a target access structure A∗, where A∗ does not
satisfy the access structures queried in Phase 1. Then the challenger
C chooses a bit b ←− {0, 1}, and returns CT ←− Encrypt(S∗, Mb)
Phase 2: It is the same as Phase 1 except Decrypt(CT∗, Sj) and
KeyGen(Sj) such that Sj |= A∗ are not allowed
2020 年 8 月 12 日

19. 19/30
CP-ABE Security Model
Guess: The adversary A outputs a bit b, and wins the game if b = b.
The advantage of the adversary A in winning the game is defined as
Adv(A) = Pr[b = b]−1/2
We say that an ABE scheme is CCA secure if for all PPT adversary
A, Adv(A) is negligible
2020 年 8 月 12 日

20. 20/30
Waters CP-ABE
additional restriction
Let e : G × G −→ GT be a bilinear map, where G and GT are multiplicative
groups with prime order p. Let g be a generator of G
Setup(1λ): Define the universe U = 1, 2, ..., k
1 Randomly choose h1, h2, ..., hk ←− G
2 Randomly choose α, a ←− Zp
3 Compute Y = e(g, g)α
, h = ga
4 Set params = (g, h, Y, {hi}k
i=1), msk = gα
5 Output (params, msk)
Encrypt(A = (L, ρ), M): Let the LSSS access structure L be an ℓ × n
matrix
1 Choose a random vector v = (s, y2, ..., yn) ←− Zn
p
2 For i = 1 to ℓ, compute λi = Li, v
3 Compute C = MYs
, C′
= gs
4 For i = 1 to ℓ, compute Ci = hλi
h−s
ρ(i)
5 Output CT = (C, C′
, {Ci}ℓ
i=1 to ℓ)
2020 年 8 月 12 日

21. 21/30
Waters CP-ABE
KeyGen(msk, S)
1 Randomly choose t ←− Zp
2 Compute K = gα
ht
, L = gt
3 For x ∈ S , compute Kx = ht
x
4 Output D = (K, L, {Kx}x∈S)
Decrypt(CT, D) Let CT and D be associated with an access
structure (M, ρ) and an attribute set S, respectively. Suppose that
S |= A and let I ∈ {1, ..., ℓ} be defined as I = {i : ρ(i) ∈ S}
1 Find {wi}i∈I such that i∈I wiMi = (1, 0, ..., 0)
2 Compute
M =
C
ω
, ω =
e(C′
, K)
i∈I(e(Ci, L)e(C′, Kρ(i)))wi )
2020 年 8 月 12 日

22. 22/30
Waters CP-ABE Correctness
e(C′
, K) = e(gs
, ga
ht
) = e(g, g)αs
e(g, g)ast
i∈I
(e(Ci = gaλi
h−s
ρ(i), L = gt
)e(C′
= gs
, Kρ(i) = ht
ρ(i)))wi
)
=
i∈I
(e(g, g)atλi
e(hρ(i), g)−st
e(g, hρ(i))st
)wi
=
i∈I
e(g, g)atwiλi
= e(g, g)at
∑
i∈I wiλi
= e(g, g)at
∑
i∈I wiMi,V
= e(g, g)ats
C
ω
=
Me(g, g)αs
e(g,g)αse(g,g)ast
e(g,g)ast
= M
2020 年 8 月 12 日

23. 23/30
Waters CP-ABE Security Proof
Definition: q-DBDHE Problem
Let a, s ←− Zp and gi = gai
. Given x= (g, g1, ..., gq, gq+2, ..., g2q, gs) and
Z ∈ GT decide if Z
?
= e(g, g)saq+1
Theorem
Waters’CP-ABE is selectively secure against chosen-plaintext attacks if the
q-DBDHE problem is hard
Given x = (g, ga, ..., gaq
, gaq+2
, ..., ga2q
, gs), Z ∈ GT , the challenger C
simulates the following CPA game for an adversary A
Init: The adversary A submits a target access structure
A∗ = (M∗, ρ∗) where M∗ ∈ Zℓ∗×n∗
p and n∗ ≤ q
2020 年 8 月 12 日

24. 24/30
Waters CP-ABE Security Proof
Setup:
1 Randomly choose α′
and set Y = e(ga
, gaq
)e(g, g)α′
, which means
α = αq+1
+ α′
2 Set h = ga
3 For x ∈ U choose randomly zx ←− Zp
4 For x /∈ U, if there is an i such that ρ∗
(i) = x, set
hx = gzx
gaMi[1]
ga2
Mi[2]
, ..., gan∗
Mi[n∗
]
where Mi[j] denotes the j-th entry of Mi; otherwise set hx = gzx
5 Return params = (g, h, Y, {hx}x∈U)
2020 年 8 月 12 日

25. 25/30
Waters CP-ABE Security Proof Phase 1 KeyGen Query
1 Find a vector w = (w1, ..., wn∗ ) such that M∗ · w = 0 and
(1, 0, ..., 0) · w ̸= 0
2 Set w1 = −1
3 Randomly choose r ←− Zp
4 Set
It can be achieved by computing
2020 年 8 月 12 日

26. 26/30
Waters CP-ABE Security Proof Phase 1 KeyGen Query
for x ∈ S
If x is not used in A∗ i.e. no ρ∗(i) = x, i ∈ {1, ..., ℓ}.
Kx = Lzx = gtzx = (gzx )t = ht
x
f x is used in A∗ i.e. exists ρ∗(i) = x, i ∈ {1, ..., ℓ}
2020 年 8 月 12 日

27. 27/30
Waters CP-ABE Security Proof Phase 1 KeyGen Query
when j = m, there is no problem of unknow gaq+1
. since
2020 年 8 月 12 日

28. 28/30
Waters CP-ABE Security Proof Challenge
1 The adversary submits two messages M0, M1
2 Randomly choose b ←− {0, 1}
3 Set C = gs
4 Compute C = MbZe(gs, gα′
)
5 Choose y′
2, ..., y′
n∗ ←− Zp
6 Set v = (s, sa + y′
2, sa2 + y′
3, ..., san∗−1 + y′
n∗ )
2020 年 8 月 12 日

29. 29/30
Waters CP-ABE Security Proof Challenge
Ci = gaλi
h−s
ρ∗(i), hρ∗(i) = gzρ∗(i)+
∑n∗
j=1 ajMi[j]
2020 年 8 月 12 日

30. 30/30
Waters CP-ABE Security Proof
if there is an adversary winning the game with non-negligible advantage,
then the challenger is able to solve the q-DBDHE problem with the same
advantage
2020 年 8 月 12 日