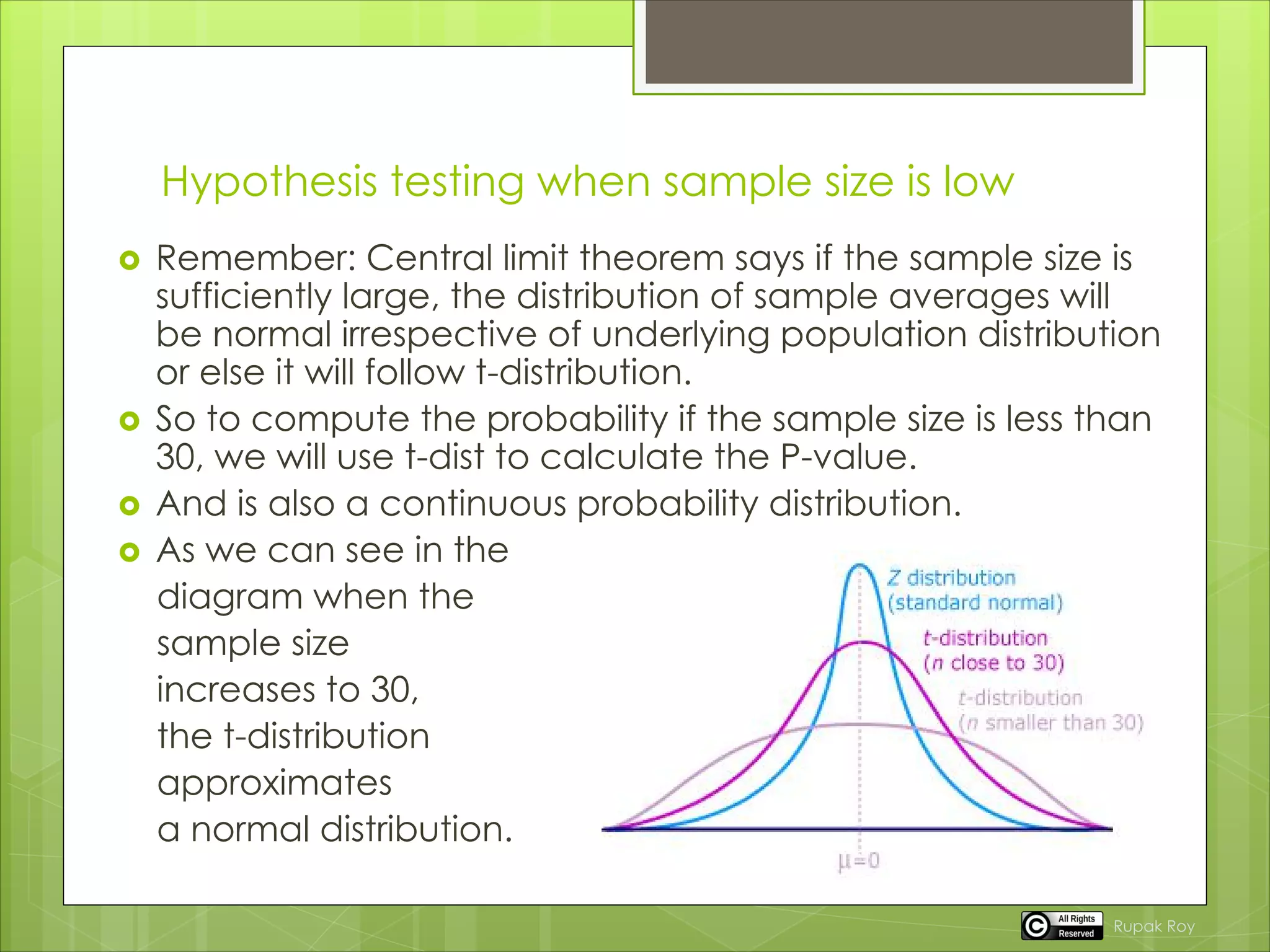
Hypothesis testing is a statistical method used to determine if there is sufficient evidence from sample data to draw conclusions about a population, involving a null hypothesis (H0) and an alternative hypothesis (H1). The significance level (alpha) helps decide whether to reject or accept the null hypothesis based on p-values, with a common threshold set at 0.05. The document also explains the Central Limit Theorem and provides examples of hypothesis testing with different distributions and sample sizes.

1. Hypothesis
Testing -I

2. Definition
 A hypothesis test is a statistical test that is used for
determining whether there is enough evidence
from the sample data to draw a conclusion for
the entire population.
 Two types of conclusions:
1. Null Hypothesis (Ho): is the hypothesis that any
observe variation in a sample is simply because of
random chance variation or we can say “the
hypothesis - that there is no significant difference
between the sample and the population, and any
observed difference is due to randomness or
experimental error.”
Rupak Roy

3. 2. Alternative Hypothesis ( Ha ):
is the hypothesis testing that is contrary to the
null hypothesis.
Examples:
If i replace the battery in my car, then my car will give
better mileage?
Null Hypothesis (Ho): no difference of mileage even if we
replace the battery of the car.
Alternative Hypothesis (Ha): difference in mileage if we
replace the battery of the car
Rupak Roy

4. Significance level i.e. alpha a
If the criteria used for rejecting the null
hypothesis is less than 5% i.e. 0.05(p-value)
then we will conclude that there is difference
between sample and population. In other
words we are rejecting the null hypothesis.
The most standard value for rejecting null
hypothesis is 0.05; however we can change
depending on our need.
Rupak Roy

5. Example
 If
P (value) > Significance level (a), then we will
accept the null hypothesis
 Else
P (value) < Significance level (a), then we will
reject the null hypothesis
Another term for saying we have rejected the
null hypothesis is Statistically Significant result.
Rupak Roy

6. Stages of Hypothesis
1. Select
Null hypothesis (Ho): no difference of mileage if we
replace the battery of the car.
Alternative Hypothesis(Ha): difference in mileage if we
replace the battery of the car.
2. Test Distribution: select appropriate distribution like
norm.dist, binom.dist, t-distribution with
significance level: alpha (a) 5% i.e. 0.05
3. P-value ( example, p = 1- norm.dist(………)=0.09
4. Result: failed to reject the null i.e. accepting the null
hypothesis and discarding the alternative hypothesis. We
will conclude that there is no difference in mileage even if
we replace the battery of the car.
Rupak Roy

7. Example
A food production unit produces a particular product of an average
weight of 10 lbs. with a standard deviation of 0.35 lbs. A random
sample of 30 units found a slightly increase of average weight by 2 lbs.
i.e. 12 lbs. So are there any issues in the product process?
Significance level (a) = 0.05
Null Hypothesis (H0): There are no issues in the production process,
what we found in the sample are due to random chance variation /
randomness.
Alternative Hypothesis (H1): There are some issues in the production
process that is leading to the increase in weight per unit.
Test Distribution: normal distribution
Rupak Roy

8. Example: continued
In Excel,
normal distribution = norm.dist( X, mean, Standard deviation, Cumulative)
where,
X =12, mean = 10, standard deviation = 0.35 and cumulative =
TRUE/False
Therefore,
= 1- norm.dist
(Because we need to calculate P-value for greater than 10 lbs.)
=1- norm.dist (12,10,0.35,TRUE)
= 5.5089E-09 i.e. less than 0.05
Since P-value is smaller than Significance level (a), we have failed to
reject the H1 i.e. accepting the alternative hypothesis and discarding the
Null hypothesis.
In other words, we will conclude that there are some issues in the
production process that leads to the increase in weight per unit of
production.
Rupak Roy

9. Terminology
Confidence level: is (1-significance level),
it refers how confident you are about your
conclusion.
So, if null hypothesis is rejected at a 5% level of
significance, then it means you are 95% (1- 0.05)
confident about your conclusion.
Again, if null hypothesis is rejected at a 1% level of
significance, then it means you are 99% (1-0.01)
confident about your conclusion.
Rupak Roy

10. Central Limit Theorem (CLT)
 The central limit theorem says irrespective of
the underlying population distribution, when
you pick a multiple random samples from an
underlying population with a sample size of at
least 30 or above. The distribution of sample
average will be normal even if the underlying
population is not normal.
Rupak Roy

11. Hypothesis testing when sample size is low
 Remember: Central limit theorem says if the sample size is
sufficiently large, the distribution of sample averages will
be normal irrespective of underlying population distribution
or else it will follow t-distribution.
 So to compute the probability if the sample size is less than
30, we will use t-dist to calculate the P-value.
 And is also a continuous probability distribution.
 As we can see in the
diagram when the
sample size
increases to 30,
the t-distribution
approximates
a normal distribution.
Rupak Roy

12. T-distance
In order to calculate t- distribution we need
t-distance i.e.
the test statistics =
Where,
(sample mean – population mean) /
( S ) standard deviation/ (N ) sample size )
Rupak Roy

13. Steps for T-distribution
 Select
null hypothesis (ho):
alternative hypothesis (h1):
 Significance level: 5%
 Test distribution: t-distribution(calculate P-value)
 Conclusion: reject the null hypothesis or accept
the null hypothesis.
Rupak Roy

14. Example
 The seller of a manufacturing company claims that
an average fluorescent light stays for 320 days. The
inspector randomly selects 10 fluorescent lights for
inspection. The sampled last with an average of 280
days along with a standard deviation of 95. What is
the likelihood that the randomly selected sample
fluorescent light would have an average life of no
more than 280 days?
Here, sample mean = 280
population mean = 320
population std. deviation = 95
sample size = 10
Rupak Roy

15.  In excel:
1) calculate t- distance
t =(280-320)/(95 / 10 )
Alternatively, (280-320)/(95/ (10^0.5))
t = - 1.331
2) use the T-distance value in Excel with the following
formula
= t.dist (t-distance, degrees of freedom, TRUE)
= t.dist( -1.331,9,TRUE) = 0.10788 = 11%
Therefore there is 11% likelihood that the average life for randomly selected bulbs is less
than 280 days
ALTERNATIVELY,
= 1-(t.dist( t-distance , degree of freedom, TRUE))
= 1-(t.dist(-1.331,9,TRUE) = 1- 0.1078= 0.89= 89%
Therefore there is 89% likelihood that the average life for 10 randomly selected bulbs is
more than 280 days
Note:
Df = degrees of freedom = N -1 ( here in the example N (samples size) = 10)
Rupak Roy

16.  Note:
Why sometimes we use
1- normal.distribution
1- t.distribution
If we have notice in any distribution, cumulative for
normal.distribution
= norm.dist(….cumulative) where
cumulative is TRUE / FALSE
TRUE (function) means < and FALSE (function) = point
probability
And what if we want > there is no function, so for that we
manually have to feed
1 – appropitate.distribution
Rupak Roy

17. What if population Std.deviation is not available
 If population standard deviation is not known,
sample deviation can be substitute for the
population standard deviation.
 Therefore, S =sample deviation / sample size
Rupak Roy

18. What if population distribution is not
normal i.e. not normal distribution?
 We are using normal distribution to calculate
p-value for hypothesis testing but it is not
always necessary that every hypothesis test
must use a normal distribution.
 If we already know the type of distribution,
then it’s better to use directly the right
distribution for hypothesis testing.
 Remember the example from our previous
slide “Stage of Hypothesis” where in point
number 2 we have mentioned that we can
choose any appropriate types of distribution.
Rupak Roy

19. Recap:
“Stages of Hypothesis”
1. Select
Null Hypothesis (Ho): no difference of mileage if we
replace the battery in the car.
Alternative Hypothesis (Ha): difference in mileage if we
replace the battery in the car
2. Test Distribution: select appropriate distribution like
norm.dist, binom.dist with significance level: alpha (a)
5%
3. P-value ( example, p = 1- norm.dist(………) )=0.09
4. Result: failed to reject the null i.e. accepting the null
hypothesis and discarding the alternative hypothesis.
We will conclude that there is no difference in
mileage even if we replace the battery of the car.
Rupak Roy

20. Next
Directional Hypothesis test
like one tail test i.e. if you have strong reason to
believe in your hypothesis.
And more.
Rupak Roy

21.  To be continued.
Rupak Roy