1. The document discusses hypothesis testing, including defining the null and alternative hypotheses, types of errors, test statistics, and testing differences between population means and differences between two samples. 2. Examples are provided to demonstrate hypothesis testing for one and two sample means. This includes stating the hypotheses, significance level, test statistic, critical region, and conclusion. 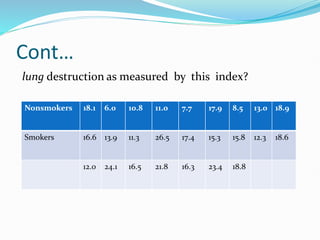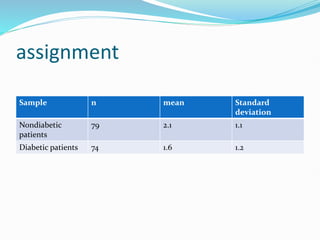3. Assignments are given applying hypothesis testing to compare lung destruction between smokers and non-smokers, serum complement activity between disease and normal subjects, and podiatric problems between elderly diabetic and non-diabetic patients.

1. By
Francis Muwonge
M-Consults

2. Introduction
Why testing of Hypothesis?
Its relevant because it helps to give us a set of
rules that lead to a decision culminating in the
acceptance or rejection of some statement or
hypothesis about the population.
Examples:
1) A medical researcher might be required to
decide on the basis of the experimental
evidence whether a certain vaccine is
superior to one presently being marketed

3. Introduction
 2.An engineer might have to decide on the basis of
sample data whether their is a diference between
the accuracy of two kinds of gauges of iron sheets
 3. A sociologist might be interested in collecting
data appropriate to enable her to decide whether
the blood type and the eye color of and individual
are independent variables?
The procedures for establishing a set of rules that lead
to the acceptance or rejection of these kinds of
statements comprise a major area of statistical inference
called Testing of hypothesis.

4. Hypothesis
A statistical hypothesis is defined as an assertion
or conjecture concerning one or more population
parameters.
 Types of hypothesis:
They are two:
1.The null hypothesis.(Ho)
2.The alternative Hypothesis(Ha).
Definition: The term null hypothesis is used to
mean any hypothesis we wish to test.

5. Some Basic Concepts in Testing
Hypothesis
The alternative hypothesis: is that hypothesis
which will contain all the alternative values to the
null hypothesis
Critical region :defined as that region which leads to
the rejection of the Null hypothesis.
Type I error: Is defined as that error committed
when we reject the null hypothesis when it is actually
true./Rejection of the null hypothesis when it is true.
Type II Error:Aceptance of the null when it is false

6. Some Basic Concepts in Testing
Hypothesis
Level of significance. Is defined as the probability
of committing type 1 error.
 Steps to testing of hypothesis.
(1) State the null hypothesis
(2) Choose the appropriate hypothesis H1 from
one of the alternatives θ>θo, θ<θo, θ≠θo.
(3) Choose a level of significance
(4) Select an appropriate test statistic and
establish the critical region.

7. Some Basic Concepts in Testing Hypothesis
(5) Compute the value of the test statistic from
the e sample data.
(6) Decision :Reject Ho if the test statistic has
a value in the critical region, otherwise ,accept
Ho.

8. •Formulation of hypothesis
 The formulation of hypothesis depends on the
question posed.
Example 1: Test the hypothesis that the population
mean is not 45.
Statistically, we write as :Ha:µ≠45
Which can be tested with Ho:µ=45
Example 2:Test the claim that the average length of
stay for chronic disease patient s is 30 days.
Ho:µ=30

9. Formulation of hypothesis
 Test the claim :
Is the population average length of stay for a chronic
disease different from 30?
Solution: Ha:µ≠30
 Test the claim:
is the average number of heart beats per minute less
than or equal to 85?.
Solution: Ha:µ≤85

10. Formulation of hypothesis
Test the claim that :
Is the average amount spent in the bookstore less than
$95?
Solution: Ha:µ<$95

11. Tests concerning the population
means
Here we follow same steps:
State the Null hypothesis
State the alternative hypothesis
Set the level of significance
Choose the aproprate test statistic
Caliculate it out
Determine the critical region
Compare coputed test value with the critical
region to make decision

12. Tests concerning the means
Reject if the test value lies in the critical region
Case (1):When the population variance is known:
Here the test statistic is :
Z=(Sample mean-µ)∕σ∕√n
Case (2): When the population variance is
unknown, but sample size is large (n≥30)
Here the test statistic is:
Z=(sample mean -µ)/s/√n

13. Tests concerning the means
Case (3):When the population variance is
unknown and sample size is small.
Here the test statistic is T=(s. mean-µ)∕S∕√n

14. Examples(1)
 In a random sample of 25 women showed a mean
pregnancy term of 272.5days.Suppose from previous
studies,σ as 15 days. Test at the 0.05 level of
significance to find if the average pregnancy term
is 268 days?
Solution:
(1) Ho : µ=268days
(2) Ha : µ≠268days
(3) α= 0.05

15. Examples(1)
(4) Appropriate test statistic.
Z=(s.mean-µ)/σ/√n
(5) Calculating it:
z=(272.5-268)/15/√25
=1.5
(6) Critical region: Critical values:
read from the Z-tables as ±1.96

16. Examples(1)
(7). Decision rule: Since Z computed does not go
beyond the critical values, we fail to reject the null
hypothesis that Ho:µ=268days
(8) Conclusion: we can conclude that there is no
evidence that an average pregnancy term is not
268days

17. Example(2)
In a random sample of 25 women showed a mean
pregnancy term of 272.5days.Suppose from previous
studies,σ was found to be 15 days. Test at 0.05 level
of significance to find out whether the average
pregnancy term does not exceed 268 days.
(1) Ho:µ ≤ 268days
(2) Ha:µ > 268days
(3) α= 0.05

18. Example(2)
(4) Appropriate test statistic
Z= (s.mean-µ)/σ/√n
(5) Calculating the Z
Z= (272.5-268)/15/√25
Z= 1.5
(6)Critical region. The critical value is 1.645

19. Assignment 1
A random sample of 10 recorded deaths in Uganda
during the past year showed an average life span of
71.8 years with a standard deviation of 8.9 years.
Does this seem to indicate that the average span
today is greeter than 70years?.Use α=0.05.
In a random sample of 20 pregnant women showed a
mean pregnancy term of 272.5 days. The sample
standard deviation was found to be 12 days. Test at the
0.05 level of significance to find out whether the
average pregnancy term is 268 days.

20. T-test
Case( 3)Conducted when the population variance is
unknown, Sample size is small.
Test statistic T=(s.maen-µ)/s/√n
T~t α,(n-1).
Example: A random sample of 20 batteries had a mean
capacity of 138.47ampere. The sample standard
deviation is found to be 2.66ampere.Test the
hypothesis at 0.05 level of significance if the average
capacity of batteries is at least 140 ampere.

21. T-test
(1) Ho: µ≥140
(2) Ha:µ<140
(3) α=0.05
(4) Test statistic T=(s.mean-µ)/s/√n
=(138.47-140)/2.66/√20
=-2.57
(5) The critical region.
t 0.05,19=-1.729

22. T-test
(6) Decision rule: We reject Ho: µ≥140 ,iff t computed
is less than the t observed.
** since t calculated = -2.57 is less than t observed=
-1.729,we reject the null hypothesis that µ≥140 and
Hence
(7) Conclude that the average capacity of batteries is
at most 140 amperes.

23. Tests concerning two samples, testing
difference between means
Hypothesis to be tested:
(1) Ho:µ1-µ2=0 , Ha : µ1-µ2≠0
(2)Ho:µ1-µ2≥0 , Ha :µ1-µ2<0
(3)Ho:µ1-µ2≤0 , Ha : µ1-µ2>0
Test statistics to be used and when?
(1) z=(s.mn1-s.mn2)-do/√σ^2/n1 + σ^2/n2
When σ1 and σ2 are known for the two populations
(2) z=(s.mn1-s.mn2)-do/√s^2/n1 + s^2/n2
when σ1 and σ2 are unknown ,but n1 and n2 are

24. Tests concerning two samples, testing
difference between means
..independently ≥ 30
(3) T =(s.mn1-s.mn2)-do/√S^2 pooled/n1 + S^2
pooled/n2
show them pooled variance
 Remark: The rest of the steps of testing hypothesis
remain the same as before

25. Tests concerning two samples, testing
difference between means
Examples :
(1) Researchers wish to know if the data they have
collected provide sufficient evidence to indicate a
difference in the mean serum uric acid level
between normal individuals and individuals with
Down’s syndrome. The data consist of serum uric
acid readings on 12 individuals with Down’s
syndrome and 15 normal individuals. The sample
means are 4.5mg/100ml and 3.4 mg/100ml.Asume that
the two samples each are drawn from a normally ..

26. Tests concerning two samples, testing
difference between means
..distributed population with a variance equal to 1 for
the drawn’s syndrome population and 1.5 for the
normal population

27. Solution
(1) Ho: µ1-µ2=0 ,
(2) Ha : µ1-µ2≠0
(3) α=0.05
(4) Appropriate test statistic.
since the population variances for the two
populations are known, then we will use the Z test
statistic
(5) calculating it

28. solution
z=(4.5-3.4)-0/√(1/12 + 1.5/15)
=2.57
(6) Critical region
± 1.96
(7) Decision
Reject Ho: µ1-µ2=0 if Z computed is greater that
critical values.

29. solution
(9) Conclusion:
Since Z computed = 2.57 is > z observed = 1.96,Ho is
rejected, and we conclude that µ1-µ2≠0 i.e based on
these results ,we can conclude that the two
population means are not equal.

30. solution
Suppose, we want to know, that if the two population
means are not the same, which one is smaller and
which one is bigger?
Solution:
Since we rejected from the upper tail, we can
further say that µ1>µ2 i.e. the mean uric acid level in
normal individuals is far higher than that of
individuals with Down’s syndrome.

31. Assignment
(2)A public health student wanted to investigate the
nature of lung destruction in the lungs of cigarette
smokers before the development of the lungs of
lifelong nonsmokers and smokers who died suddenly
outside the hospital of respiratory causes. A larger
score indicates greater lung damage.
The data below gives data that was collected from 16
smokers and 9 non smokers. Use the data to find out
if we can conclude, in general that smokers have
greater

32. Cont…
lung destruction as measured by this index?
Nonsmokers 18.1 6.0 10.8 11.0 7.7 17.9 8.5 13.0 18.9
Smokers 16.6 13.9 11.3 26.5 17.4 15.3 15.8 12.3 18.6
12.0 24.1 16.5 21.8 16.3 23.4 18.8

33. Assignment
(3) A researcher wishes to know if two populations
differ with respect to the mean value of total
serum complement activity(CH50).The data consists
of (CH50) determinations on n2=20 apparently
normal subjects and n1=10 subjects with disease
The sample means and standard deviations are
s.maen 1=62.6 s1= 33.8
s.mean 2=47.2 s2=10.1

34. assignment
Formulate the appropriate hypothesis and test
them at 0.05 level of significance
(4) Ashaba E. conducted a study to determine if the
prevalence and nature of podiatric problems in
elderly diabetic patients are different from those
found in a similarly aged group of non diabetic
patients. Subjects ,who were seen in outpatient
clinics, were 70-90 years. Among the investigators’
findings were the following statistics with respect to
scores on measurement on the deep tendon

35. assignment
Sample n mean Standard
deviation
Nondiabetic
patients
79 2.1 1.1
Diabetic patients 74 1.6 1.2

36. assignment
On basis of this data, can we conclude ,on average
that diabetic patients have reduced deep tendon
reflexes when compared to nondaibatic patients of
the same age? Test it at 0.01 level of significance

37. Reading assignment
Read about paired comparisons

38. Hypothesis testing for population
proportions
Just guide them manually on board
Formulate all possible hypothesis
 test statistic for large samples
Z= (Р-Рo)/√pq/n
For two sample proportions
Z= (P1-P2)-(P1-P2)0/√(P1(1-P1)/n1 + p2(1-p2)/n2