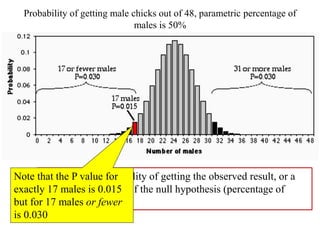
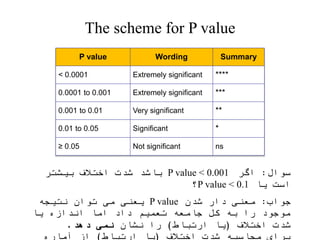
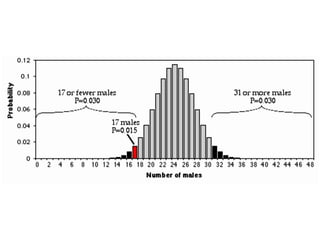
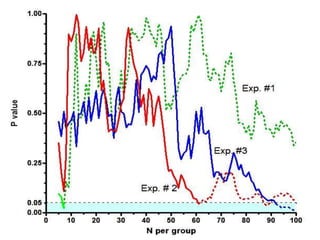
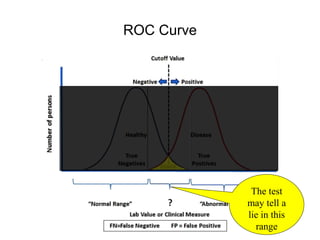
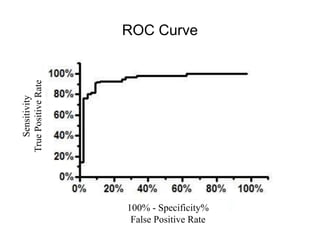
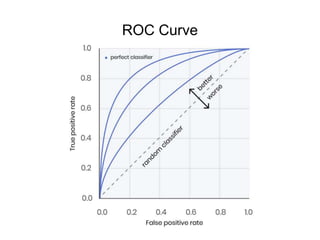
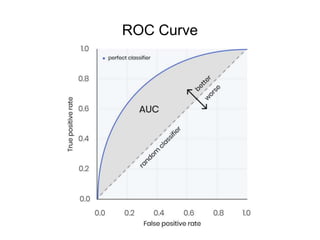
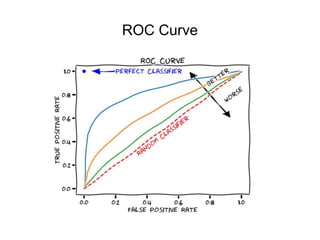
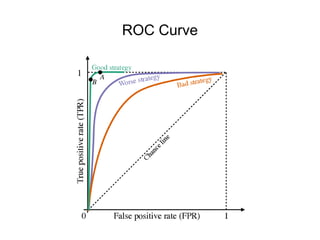
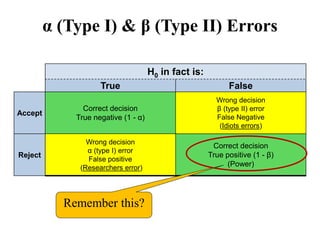
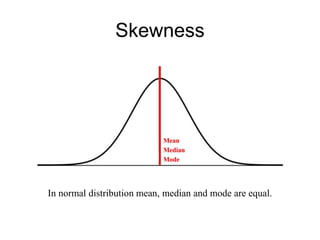
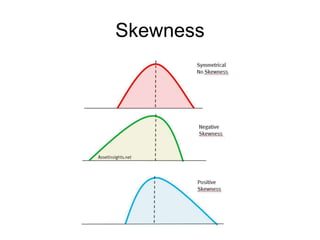
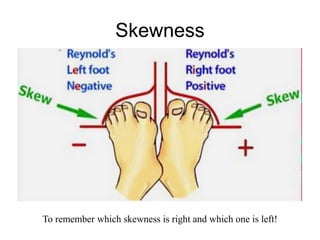
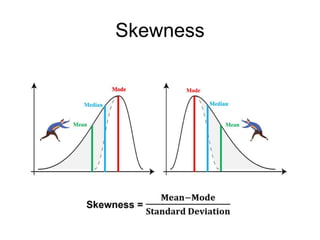
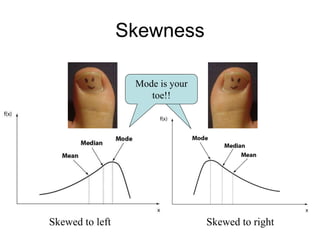
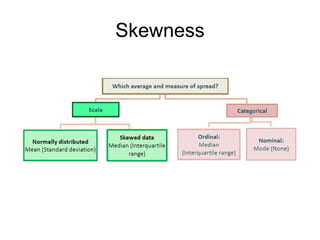
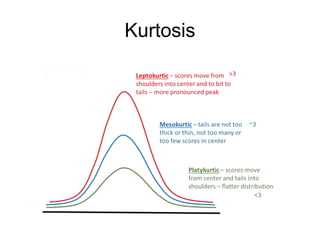
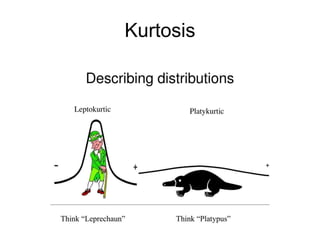
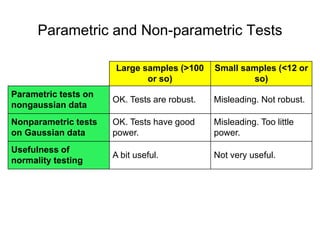
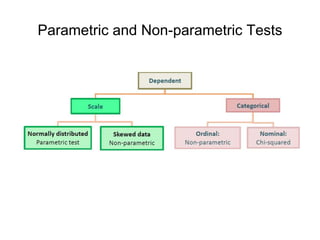
This document discusses key concepts in applied statistics including hypothesis testing, p-values, types of errors, sensitivity and specificity. It provides examples and explanations of these topics using scenarios about testing if feeding chickens chocolate changes the gender ratio of offspring. Hypothesis testing involves defining the null and alternative hypotheses and using a statistical test to either reject or fail to reject the null hypothesis based on the p-value. Type I and type II errors in hypothesis testing are explained. Sensitivity and specificity in diagnostic tests are introduced using an example about detecting if a car is being stolen.

1. By:
M. H. Farjoo M.D, Ph.D, Bioanimator
Shahid Beheshti University of Medical Sciences
Instagram: @bio_animation
Applied Statistics
Part 2

2. Applied Statistics
part 2
 Hypothesis Testing & P Value
 α & β Errors
 Sensitivity & Specificity, PPV & NPV
 True/False Positive/Negative
 ROC Curves
 Power and the Basement Story
 Normality Tests
 Parametric and Non-parametric Tests

3. Hypothesis Testing & P Value
 In analytical statistics we try to prove our intervention
has made a difference (improvement).
 This is done by comparing the means of the 2 (or
more groups) under study.
 The difference between the means should be large
enough to accept the difference is real and not by luck
or chance!
 How much large is large enough?
 This is answered by statistical tests, not common
sense!

4. Hypothesis Testing & P Value
 Assume you are studying sex determination in chickens.
 In aviculture, female chicks are more valuable than male
chicks.
 If you could figure out a way to breed more female chicks
than males, you could get Nobel Prize (WOW!!)
 During your sleep you are inspired from heaven that
chocolate can change gender ratio in chickens!
 So you assume or “Hypothesize” that feeding the
chickens with chocolate leads to Nobel Prize!

5. We feed a bunch of female chickens by chocolate and…

6. The next generation (population) is this!

7. We take a 48 random sample from the population

8. Hypothesis Testing & P Value
 If you get 25 female and 23 male chicks anyone can say
they could easily result from chance.
 If you got 47 females and 1 male, it would be extremely
unlikely to happen due to luck (chance).
 What if you had 31 females and 17 males?
 That is definitely more females than males, but is it due to
chance or not?
 We need to test our hypothesis and calculate the
Probability (P Value) of getting a difference that large by
chance.

9. Hypothesis Testing & P Value
 To test any intervention about our assumption (guess
or theory), we consider 2 hypotheses:
1. The hypothesis which at the bottom of our heart we
die to be true (H1 or Alternative Hypothesis).
2. The hypothesis which we do anything (even torturing
data!) to show it is wrong. (H0 or Null Hypothesis).
 H0 is boring, disappointing, and causes sorrow, but
H1 is exciting, and causes happiness (usually not
always).

10. Alternative hypothesis
(H1) is true.
Null hypothesis
(H0) is true.
Your face (usually, but not always)

11. Hypothesis Testing & P Value
 The character “0” (zero) in H0 means one or all of
the followings:
 The difference between the means is zero, so there is no
difference.
 The effect of your intervention is zero, so your time, life
and money is wasted, and the intervention had no effect
(sorry!).
 The condition (disease, event, or happening) does not exist.
 The groups (2 or more) actually are the same.
 The samples are from the same or one population.

12. Hypothesis Testing & P Value
 In statistical tests, we do NOT prove H1, we Reject H0
(why?).
 Because Proving a hypothesis means you are 100% sure
(but you can never be!)
 when you have treated merely a sample (even the best
sample in the world history), you never are 100% sure
about the population.
 We just claim with a reasonable certainty that H0 cannot
be true and is rejected.
 Note we do NOT prove H0 is wrong, but according to
evidence, we just reject it, and accept H1.

13. Hypothesis Testing & P Value
 The statistical concept of 'significant' vs. 'not
significant' is comparable to 'guilty' vs. 'not guilty'.
 If the evidence proves the defendant fault beyond a
reasonable doubt, the verdict is 'guilty‘, else 'not
guilty'.
 “Not guilty” does not mean the defendant is innocent.
 It just means that the evidence was not strong enough
to persuade the judge that the defendant was guilty.

14. Hypothesis Testing & P Value
 The arbitrary significance level (critical value, alpha)
for accepting or rejecting H0 is 0.05 or 5%.
 You must choose your significance level before you
collect the data.
 If you choose a significance level other than 0.05,
people will be skeptical!
 You must be able to justify your choice.
 Do not forget: "Statistically significant" does not
mean the effect is large or scientifically important.

15. Hypothesis Testing & P Value
 P value is the probability of getting the, difference
(result, effect, etc.) or a more extreme one if the null
hypothesis is true.
 If the P value is small (≤ 5% of critical value) then:
 There is a 5% or less chance that the effect, difference or
result is by chance, so it is REAL.
 H0 is rejected and H1 accepted. (happy face)
 If the P value is large (> 5% of critical value) then:
 There is more than 5% chance that the effect, difference or
result is a random coincidence, so it is NOT real.
 H1 is rejected and H0 accepted. (crying face)

16. P value is the probability of getting the observed result, or a
more extreme result, if the null hypothesis (percentage of
males is 50%) is true.
Probability of getting male chicks out of 48, parametric percentage of
males is 50%
Note that the P value for
exactly 17 males is 0.015
but for 17 males or fewer
is 0.030

17. The scheme for P value
P value Wording Summary
< 0.0001 Extremely significant ****
0.0001 to 0.001 Extremely significant ***
0.001 to 0.01 Very significant **
0.01 to 0.05 Significant *
≥ 0.05 Not significant ns
‫سوال‬
:
‫اگر‬
P value < 0.001
‫باشد‬
‫بیشتر‬ ‫اختالف‬ ‫شدت‬
‫یا‬ ‫است‬
P value < 0.1
‫؟‬
‫جواب‬
:
‫شدن‬ ‫دار‬ ‫معنی‬
P value
‫یعنی‬
‫نتیجه‬ ‫توان‬ ‫می‬
‫اندازه‬ ‫اما‬ ‫داد‬ ‫تعمیم‬ ‫جامعه‬ ‫کل‬ ‫به‬ ‫را‬ ‫موجود‬
‫یا‬
‫شدت‬
‫اختالف‬
(
‫ارتباط‬ ‫یا‬
)
‫نشان‬ ‫را‬
‫نمی‬
‫دهد‬
.
‫برای‬
‫اختالف‬ ‫شدت‬ ‫محاسبه‬
(
‫ارتباط‬ ‫یا‬
)
‫از‬
‫آماره‬

18. Hypothesis Testing & P Value
 What if after “chocolate party” the number of female
offspring is 17 (or fewer) out of 48?
 It depends on “one-tail” or “two-tail” P value.
 One-tail P value:
 H0 : The proportion of males is 0.5 or more
 H1 : The proportion of males is less than 0.5
 P value is 3% in one direction (and is significant)
 Two-tail P value:
 H0 : The proportion of males is 0.5
 H1 : The proportion of males is different from 0.5
 P value is 3% in one direction + 3% in opposite direction =
6% (and is not significant)

20. Hypothesis Testing & P Value
 A one-tail test is used when previous data, or
common sense dictates the difference can only go in
one direction.
 Any time a deviation in either direction would be
interesting, you should use the two-tailed probability.
 It is almost always prudent to use two-tail P value.

21. Hypothesis Testing & P Value
 Advice: Don't keep adding subjects until you hit
'significance'.
 This is a commonly used and tempting approach
which leads to misleading results.
 It is important that you choose a sample size and stick
with it.
 You will fool yourself if you stop when you like the
results, but keep going when you do not.

23. ‫رودخانه‬ ‫در‬ ‫فیل‬
Elephant

24. Hypothesis Testing & P Value (α)
Hands-on practice
 To calculate P Value in Excel (eg: in a t test):
 =T.TEST(array1, array2, tails, type)
 To calculate P Value in SPSS (eg: in a paired t test):
 Analyze => Compare means => paired-samples T Test
=> add the 2 groups => OK
 To calculate P Value in Prism (eg: in a paired t test):
 Analyze => Column analysis => t tests (and
nonparametric tests) => OK

25. H0 in fact is:
True False
Accept
Correct decision
True negative (1 - α)
Wrong decision
β (type II) error
False Negative
(Idiots errors)
Reject
Wrong decision
α (type I) error
False positive
(Researchers error)
Correct decision
True positive (1 - β)
(Power)
α (Type I) & β (Type II) Errors
Any question?

26. α (Type I) Error, False Positive
Researchers Error
You are pregnant!

27. β (Type II) Error, False Negative
Idiots Error
You are NOT pregnant!

28. ‫شیرها‬ ‫خانواده‬

29. Sensitivity & Specificity
•
‫دزده‬ ‫آقا‬ ‫ماجرای‬
!
(
‫بعدی‬ ‫اسالید‬ ‫دو‬ ‫و‬ ‫اسالید‬ ‫این‬
‫است‬ ‫شده‬ ‫تهیه‬ ‫احمدی‬ ‫عماد‬ ‫سید‬ ‫آقای‬ ‫توسط‬
)
•
‫سوال‬
:
‫ماشین؟‬ ‫دزد‬ ‫میگن‬ ‫کسی‬ ‫چه‬ ‫به‬
–
‫و‬ ‫کنه‬ ‫روشن‬ ‫رو‬ ‫ماشین‬ ،‫فرمون‬ ‫پشت‬ ‫بشینه‬ ‫که‬ ‫کسی‬
‫علی‬ ‫یا‬
!
•
‫ماشینتون‬ ‫خواست‬ ‫دزد‬ ‫اگه‬ ‫دارین‬ ‫دوست‬ ‫شما‬
‫بگیرین‬ ‫مچشو‬ ‫بدزده‬ ‫رو‬
!
•
‫سوال‬
:
‫عنوان‬ ‫به‬ ‫آدمو‬ ‫یه‬ ‫میشه‬ ‫جوری‬ ‫چه‬
‫گرفت؟‬ ‫دزد‬
–
‫خوبیه؟‬ ‫راه‬ ‫آیا‬ ،‫ماشین‬ ‫نگهبان‬
!
–
‫ارزان‬ ‫حل‬ ‫راه‬
‫تر‬
:
‫دزدگیر‬ ‫نصب‬
(
‫با‬
shock sensor
)
‫ماشین‬ ‫روی‬
•
‫حاال‬
2
‫دیگه‬ ‫سوال‬ ‫تا‬
:
1
)
‫آیا‬
‫همه‬ ‫دزدگیر‬

30. •
‫که‬ ‫کنین‬ ‫مي‬ ‫زندگي‬ ‫اي‬ ‫محله‬ ‫در‬ ‫کنید‬ ‫فرض‬
‫اینه‬ ‫ماشینتون‬ ‫و‬ ‫زیاده‬ ‫دزد‬
!
•
‫نزدیک‬ ‫بهش‬ ‫احدی‬ ‫میدین‬ ‫ترجیح‬ ‫طبیعتا‬
‫حالل‬ ‫نظر‬ ‫یک‬ ‫بخواد‬ ‫اگر‬ ‫حتی‬ ‫نشه‬
!
‫بندازه‬
‫شکلیه‬ ‫چه‬ ‫توش‬ ‫ببینه‬ ‫و‬
.
•
‫یا‬ ‫حساس‬ ‫که‬ ‫میزاریم‬ ‫دزدگیری‬ ‫پس‬
sensitive
‫باشه‬
Sensitivity & Specificity

31. Sensitivity & Specificity
•
‫کنید‬ ‫فرض‬ ‫حاال‬
‫و‬ ‫اینه‬ ‫ماشینتون‬
‫محله‬ ‫تو‬
‫آدمای‬ ‫ی‬ ‫محله‬ ‫که‬ ‫کنین‬ ‫می‬ ‫زندگی‬ ‫ای‬
‫باکالسه‬
!
•
‫دزد‬ ‫انگ‬ ‫کسی‬ ‫به‬ ‫نمیشه‬ ‫راحتی‬ ‫این‬ ‫به‬
‫جد‬ ‫هفت‬ ،‫دزد‬ ‫بگیم‬ ‫کسی‬ ‫به‬ ‫اگر‬ ‫و‬ ‫چسبوند‬
‫مکافات‬ ‫و‬ ‫میشن‬ ‫دزد‬ ‫خودمون‬ ‫آباد‬ ‫و‬
‫داریم‬
.
•
‫حتی‬ ،‫نکنین‬ ‫ریسک‬ ‫میدین‬ ‫ترجیح‬ ‫طبیعتا‬
‫ماشین‬ ‫به‬ ‫هم‬ ‫جانانه‬ ‫ضربه‬ ‫چند‬ ‫طرف‬ ‫اگر‬
‫باشه‬ ‫زده‬
!
•
‫یا‬ ‫ویژه‬ ‫که‬ ‫میزاریم‬ ‫دزدگیری‬ ‫پس‬
specific

32. The Woman in fact is:
Not Pregnant Pregnant
Test -
Correct result
True negative (1 - α)
Condition or test Negative
(Specific Test)
Wrong result
β (type II) error
False Negative
(Idiots errors)
Test +
Wrong result
α (type I) error
False positive
(Researchers error)
Correct result
True positive (1 - β)
Condition or test Positive
(Sensitive Test, Power)
Specificity =
True Neg. / (True Neg. + False Pos.)
Sensitivity=
True Pos./ (True Pos. + False Neg.)
Sensitivity & Specificity
Any question?

33. Sensitivity and specificity
A sensitive test:
Detects those who have the condition
‫کند‬ ‫می‬ ‫گزارش‬ ‫مثبت‬ ‫را‬ ‫مثبت‬ ‫نمونه‬ ،‫حساس‬ ‫تست‬
‫میشود‬ ‫مثبت‬ ‫باردار‬ ‫خانم‬ ‫در‬ ‫حاملگی‬ ‫تست‬ ‫یعنی‬
‫اما‬
‫است‬ ‫ممکن‬
‫منفی‬ ‫نمونه‬ ‫چند‬ ،‫آن‬ ‫بر‬ ‫عالوه‬
‫هم‬ ‫را‬
‫مثبت‬ ‫اشتباه‬ ‫به‬
‫گزارش‬
‫تست‬ ‫یعنی‬ ‫کند‬
‫اشتباه‬ ‫به‬ ،‫نیست‬ ‫باردار‬ ‫که‬ ‫خانمی‬ ‫در‬ ‫حاملگی‬
‫میشود‬ ‫مثبت‬
A specific test:
Rejects those NOT having the condition
‫منفی‬ ‫را‬ ‫منفی‬ ‫نمونه‬ ،‫باال‬ ‫ویژگی‬ ‫با‬ ‫تست‬
‫می‬ ‫گزارش‬
‫کند‬
،‫نیست‬ ‫باردار‬ ‫که‬ ‫خانمی‬ ‫در‬ ‫حاملگی‬ ‫تست‬ ‫یعنی‬
‫میشود‬ ‫منفی‬
‫اما‬
‫مثبت‬ ‫نمونه‬ ‫چند‬ ،‫آن‬ ‫بر‬ ‫عالوه‬ ‫است‬ ‫ممکن‬
‫گزارش‬ ‫منفی‬ ‫هم‬ ‫را‬
‫کند‬
،‫است‬ ‫باردار‬ ‫که‬ ‫خانمی‬ ‫در‬ ‫حاملگی‬ ‫تست‬ ‫یعنی‬
‫میشود‬ ‫منفی‬ ‫اشتباه‬ ‫به‬

34. Positive Predictive Value (PPV)
Negative Predictive Value (NPV)
 A patient test is positive for corona virus! What is the
next step?
 Rest in home?
 Outpatient therapy?
 Hospitalization?
 A patient test is negative for corona virus! What is the
next step?
 Go anywhere you wish?
 Repeat test?
 Another test? (better test or gold standard test?)

35. Example
Suppose the fecal occult blood screen test is used in 2030
people to look for bowel cancer:
PPV & NPV

36. Sensitivity & Specificity, PPV & NPV
 Bottom line:
 A sensitive test finds patients.
 A specific test finds healthy people.
 Sens. and spec. are useful before doing the test, so
they help us to choose a test.
 PPV and NPV are useful after doing the test, so
they help us to decide about the patient.

38. ‫پلیکانها‬ ‫گروه‬

39. Sensitivity & Specificity, PPV & NPV
Hands-on practice
 To calculate sensitivity, specificity, PPV and NPV in
Excel and SPSS :
 Calculate manually!
 To calculate sensitivity, specificity, PPV and NPV in
Prism:
 Contingency (from welcome screen) => Analyze =>
choose appropriate option

40. True/False Positive/Negative
 The costs of α and β errors determine the P value, and your
study design.
 With a P value of 0.05, there is a 5% chance of rejecting H0,
even if it is true.
 A P value ≥ 0.05 has both of the following effects:
 Increases false positive (finding a fake “female maker” agent in
chickens)
 Decreases false negative (missing a real but not very potent
“female maker” agent in chickens)
 A P value lower than 0.05, does the reverse!
 My advice: stick to the two-tail, 5% P value!

41. 1000 sample tested to kill
parasites, 500 are really effective
(we do not know which ones)
P ≤ 0.05
Not Effective (But we
wrongly think is effective) (0.05 * 500) = 25
Really Effective 500
Total (true & False) effective 525 (5% is FP)
True/False Positive/Negative
FP = False Positive

42. 1000 samples tested to grow
hair, 1 is really effective (we do
not know which one)
P ≤ 0.05
Not Effective (But we wrongly
think is effective)
~ 50 (0.05 * 999)
Effective 1
Total (true & False) effective 51(98% is FP)
True/False Positive/Negative
FP = False Positive

43. Just 1 sample tested (we do not know
whether it is effective or not)
P ≤ 0.05
For parasite killing the result is quite reliable (FP was 5%)
For hair growth the result is Not reliable (FP was 98%)
True/False Positive/Negative
if you expect that the null hypothesis is
probably true, a statistically significant
result is probably a false positive! (sorry
again!).
In this case we require a much
lower P value to reject a null hypothesis
that you think is probably true.
FP = False Positive

44. ‫کوهستان‬ ‫در‬ ‫فیل‬

45. ROC Curve
The test
may tell a
lie in this
range

46. ROC Curve

47. ROC Curve

48. ROC Curve
 How do you decide where to draw the threshold between
'normal' and 'abnormal' test results?
 A receiver-operating characteristic (ROC) curve helps to
decide between sensitivity and specificity.
 You can have higher sensitivity or higher specificity, but
not both (unless you develop a better test).
 It depends on the situation, to choose between sensitivity
over specificity or vice versa.
 ROC curves are used frequently in pediatric and
diagnostic imaging devices.

49. Sensitivity
True
Positive
Rate
ROC Curve
100% - Specificity%
False Positive Rate

50. ROC Curve

51. ROC Curve

52. ROC Curve

53. ROC Curve

54. A jaguar stands on a tree branch in Pantanal, Brazil ‫درخت‬ ‫روی‬ ‫جگوار‬

55. Hands-on practice
ROC Curve
 To calculate ROC Curve in SPSS:
 Analyze => ROC Curve...
 To calculate ROC Curve in Prism:
 Column (from welcome screen) => ROC Curve =>
Analyze => Column Analysis => ROC Curve

56. Power and the Basement Story
 Power is the ability to find a real difference so it is is the
correctness of rejecting H0.
 Power is the fraction of experiments that you expect to
yield a "statistically significant" P value.
 Power is between 0 and 1 (0% and 100%).
 How much power is needed? 80% power is common.
 The choice of power depend on the consequence of
making a Type II error.

57. H0 in fact is:
True False
Accept
Correct decision
True negative (1 - α)
Wrong decision
β (type II) error
False Negative
(Idiots errors)
Reject
Wrong decision
α (type I) error
False positive
(Researchers error)
Correct decision
True positive (1 - β)
(Power)
α (Type I) & β (Type II) Errors
Remember this?

58. Power and the Basement Story

59. Power and the Basement Story

60. Power and the Basement Story
 The time searching the basement = sample size.
 The size of the tool = effect size
 The messiness of the basement = standard deviation of your data.

62. Normality Tests
 Some statistical tests compare the goodness-of-fit of a
data set to the normal distribution.
 Generally they are not recommended, because they are
not very applicable!
 In small samples they are not accurate, and in large
samples they are not that useful!
 Deviations from normal distribution, causes skewness
and/or kurtosis.
 Normality tests calculate these deformations and analyze
deviations from bell shaped normal distribution.

63. Skewness
In normal distribution mean, median and mode are equal.

64. Skewness

65. Skewness
To remember which skewness is right and which one is left!

66. Skewness

67. Mode is
your toe!!
Skewed to right
Skewed to left
Mode is your
toe!!
Skewness

68. Skewness

69. Skewness

70. Kurtosis

71. Kurtosis

72. kurtosis

73. Normality Tests
 D'Agostino-Pearson test is preferred.
 It is a versatile and powerful normality test.
 Shapiro-Wilk test, works very well if every value is
unique, but not when there are ties (identical values).
 Kolmogorov-Smirnov (KS) test, is obsolete.
 Contrary to the majority of hypothesis tests, in normality
test, you wish the H0 (null hypothesis) be true.
 You wish there is no difference between your data and
normal distribution, and H0 declares this.

75. Skewness & kurtosis
Hands-on practice
 To calculate Skewness & kurtosis in Excel:
 For skewness: =Skew => select range of data
 For kurtosis: =Kurt => select range of data
 To calculate Skewness & kurtosis in SPSS:
 Analyze => Reports => Case Summaries => Statistics
 Analyze => Descriptive Statistics => Frequencies => Statistics =>
Skewness and kurtosis check boxes
 Analyze => Descriptive Statistics => Descriptives => Options =>
Skewness and kurtosis check boxes
 Analyze => Descriptive Statistics => Explore => Statistics =>
Descriptive check box
 To calculate Skewness & kurtosis in Prism:
 Analyze => Column Analysis => Column statistics => Skewness
and kurtosis check box

76. Normality Tests
Hands-on practice
 To calculate normality tests in SPSS:
 Analyze => Descriptive Statistics => Explore => select
“Both” or “Plots” in the Display group to enable the
Plots button => Plots button => check “normality plots
with test”
 To calculate normality tests in Prism:
 Analyze => Column Analysis => Column statistics =>
Under “Test if the values come from a Gaussian
distribution” => check the proper check box

77. Parametric and Non-parametric Tests
 A normal distribution is described by just two
parameters, the mean and the standard deviation.
 All normal distributions with the same mean and SD
will be exactly the same shape.
 Some tests treat data by these two parameters (mean
& SD), so they are called parametric tests.
 Parametric tests assume your data fit the normal
distribution.

78. Parametric and Non-parametric Tests
 If your variable is NOT normally distributed, using a
parametric test increases a false positive result.
 Biological data distribution is never precisely normal.
 But many kinds of biological data are bell-shaped enough
to be considered normal.
 Parametric tests work well even if the distribution is
almost normal (especially with large samples).
 Simulation studies, have shown that the false positive rate
is not affected very much.

79. Parametric and Non-parametric Tests
 Do not worry about normality unless your data appear
very, very non-normal to you.
 There is not any rule on how much non-normality is
too much for a parametric test.
 You should look at what other people do and follow
them even if the non-normality doesn't seem that bad
to you.
 When in Rome, do as the romans do!

80. Parametric and Non-parametric Tests
 If data distribution looks like normal, but is skewed,
try data transformations to get more normal shape.
 If after transformation, data still look severely non-
normal, it is still okay to use a parametric test.
 It is better to collect some data, check the normality,
and decide on a transformation before actual
experiment.
 Otherwise, people think you tried different
transformations to find what you desire.

81. Parametric and Non-parametric Tests
 The Non-parametric tests do not assume normal
distribution.
 Non-parametric tests assume the data in different groups
have the same distribution shape as each other.
 If this is violated (one group is skewed to the left, another
to the right), a non-parametric test is not better than a
parametric one.
 As a rule of thumb, If you plan to use a nonparametric
test, compute the sample size required for a parametric
test and add 15%.

82. Parametric and Non-parametric Tests
 Both conventional and nonparametric tests have little
power in small samples (less than 12 or so) if used
mistakenly.
 Do NOT use this approach:
 First perform a normality test
 If the P value is low, conclude the data are not normal
 Choose a nonparametric test.
 Otherwise choose a conventional test.

83. Large samples (>100
or so)
Small samples (<12 or
so)
Parametric tests on
nongaussian data
OK. Tests are robust. Misleading. Not robust.
Nonparametric tests
on Gaussian data
OK. Tests have good
power.
Misleading. Too little
power.
Usefulness of
normality testing
A bit useful. Not very useful.
Parametric and Non-parametric Tests

84. Parametric and Non-parametric Tests
 To choose between parametric / non-parametric test
you should know:
 Main research question
 Variables that answer the research question
 The dependent (outcome) variable, and its type
 The independent (explanatory) variables, and their
type
 Are you looking for relationship or difference?
 Are there repeated measurements of the same variable
for each subject?

85. Parametric and Non-parametric Tests

87. Thank you
Any question?