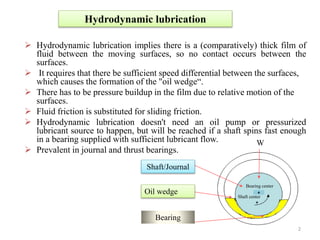
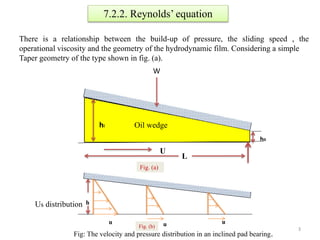
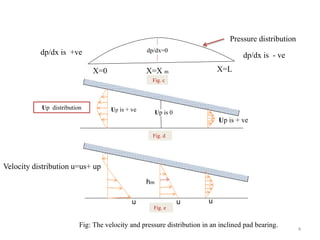
The document discusses hydrodynamic lubrication, which occurs when there is a thick film of fluid between moving surfaces so that contact does not occur. For hydrodynamic lubrication to happen, there needs to be sufficient speed difference between the surfaces to form an "oil wedge" and build up pressure in the fluid film from their relative motion. Reynolds' equation describes the relationship between pressure buildup, sliding speed, viscosity, and geometry of the hydrodynamic film. The document presents diagrams showing the velocity and pressure distributions in an inclined pad bearing under hydrodynamic lubrication conditions.

1. Presented By : BASHAR MD KHAIRUL
Student ID:15595901
Masters Student
Graduate School of Science & Engineering
Saga University
1
Advanced Lubrication Engineering
Hydrodynamic lubrication
(Friday January 22, 2016 @ multipurpose lecture room)

2. Hydrodynamic lubrication
 Hydrodynamic lubrication implies there is a (comparatively) thick film of
fluid between the moving surfaces, so no contact occurs between the
surfaces.
 It requires that there be sufficient speed differential between the surfaces,
which causes the formation of the "oil wedge“.
 There has to be pressure buildup in the film due to relative motion of the
surfaces.
 Fluid friction is substituted for sliding friction.
 Hydrodynamic lubrication doesn't need an oil pump or pressurized
lubricant source to happen, but will be reached if a shaft spins fast enough
in a bearing supplied with sufficient lubricant flow.
 Prevalent in journal and thrust bearings.
Shaft/Journal
Oil wedge
Bearing
+
W
Bearing center
+
Shaft center
2

3. 7.2.2. Reynolds’ equation
There is a relationship between the build-up of pressure, the sliding speed , the
operational viscosity and the geometry of the hydrodynamic film. Considering a simple
Taper geometry of the type shown in fig. (a).
Oil wedge
W
hi
ho
U
L
h
u
Fig. (a)
u u
Fig. (b)
Us distribution
Fig: The velocity and pressure distribution in an inclined pad bearing.
3

4. Fig. c
X=0 X=X m X=L
dp/dx is +ve dp/dx is - ve
dp/dx=0
Pressure distribution
Up is + ve
Up is + ve Up is 0
Up distribution
Fig. d
u
hm
uu
Fig. e
Velocity distribution u=us+ up
Fig: The velocity and pressure distribution in an inclined pad bearing.
4

5. The fluid that is in contact with the moving surface moves with the moving surface with the
velocity U surface . The film to a continuous shearing so that the velocity Us of the film at
any value of Y is given by
us=U
(𝒉−𝒚)
𝒉
The form of us is shown in fig b; us is +U at y=0 and zero at y=h. This is known as Couette flow.
With converging walls the relationship between the fluid flow and the pressure build-up
(Poiseuille flow) is ,
up=
𝟏
𝟐𝜼
(
−𝒅𝒑
𝒅𝒙
) y(h-y)
7.1
The values of dp/dx vary with x, and assume that this variation is as shown in figure c . The
form of up is according to fig. d and up is zero at y=0 and y=h. At the entry section dp/dx will
be positive, near the center it will be zero , and after this point it will be negative . This gives rise
to the patterns of up shown in fig. d.
The pressure gradient and the shear flow are the only two causes of fluid flow , the resultant
velocity of the fluid follows the patterns shown in fig. e is given by
u=us + up
=U
(𝒉−𝒚)
𝒉
+
𝟏
𝟐𝜼
(
−𝒅𝒑
𝒅𝒙
) y(h-y)
7.1
7.2
7.3
5

6. Neglecting any side flow , the area of an element of film is 1×dy per unit width of the film. The
quantity flowing per unit time is thus u dy for each element area and the total flow q is given by
q= 𝟎
𝒉
𝒖 𝒅𝒚
Substituting for u from equation (7.3) and integrating
𝑞 = 0
ℎ
𝑈.
ℎ−𝑦
ℎ
𝑑𝑦 + 0
ℎ 1
2𝜂
−𝑑𝑝
𝑑𝑥
𝑦ℎ −
1
2𝜂
−𝑑𝑝
𝑑𝑥
𝑦2 𝑑𝑦
𝒒=
𝑼𝒉
𝟐
+
𝒉𝟑
𝟏𝟐𝜼
−𝒅𝒑
𝒅𝒙
.
7.4
At some point the pressure is maximum and
𝒅𝒑
𝒅𝒙
=0; let the value of h at this point be hm
(maximum) whence, 𝑞=
𝑈ℎ
2
+
ℎ3
12𝜂
−𝑑𝑝
𝑑𝑥
=0 [As some point the pressure is maximum;
𝒅𝒑
𝒅𝒙
=0]
𝑞=h(
𝑈
2
) [note: let the value of h at this point be hm]
qm=hm(
𝑼
𝟐
)
.
7.5
.
6
.
So,

7. But the flow through the film must be the same at all values of h so that,qm=q and thus,
𝒒 =
𝑼𝒉
𝟐
+
𝒉𝟑
𝟏𝟐𝜼
−𝒅𝒑
𝒅𝒙
𝒒= hm(
𝑼
𝟐
)
So, 𝒒 = hm(
𝑼
𝟐
) =
𝑼𝒉
𝟐
+
𝒉𝟑
𝟏𝟐𝜼
−𝒅𝒑
𝒅𝒙
2 𝑑𝑝
𝑑𝑥
ℎ3
12𝜂
=
𝑈ℎ
2
-
hm 𝑈
2
𝟐 𝒅𝒑
𝒅𝒙
= 𝟏𝟐𝜼 (
𝑼
𝟐
) (
𝒉−𝒉𝒎
𝒉𝟑
)
7.4
7.5
7.6
7.7
7

8. どうもありがとうございます.
Thank you very much.
8