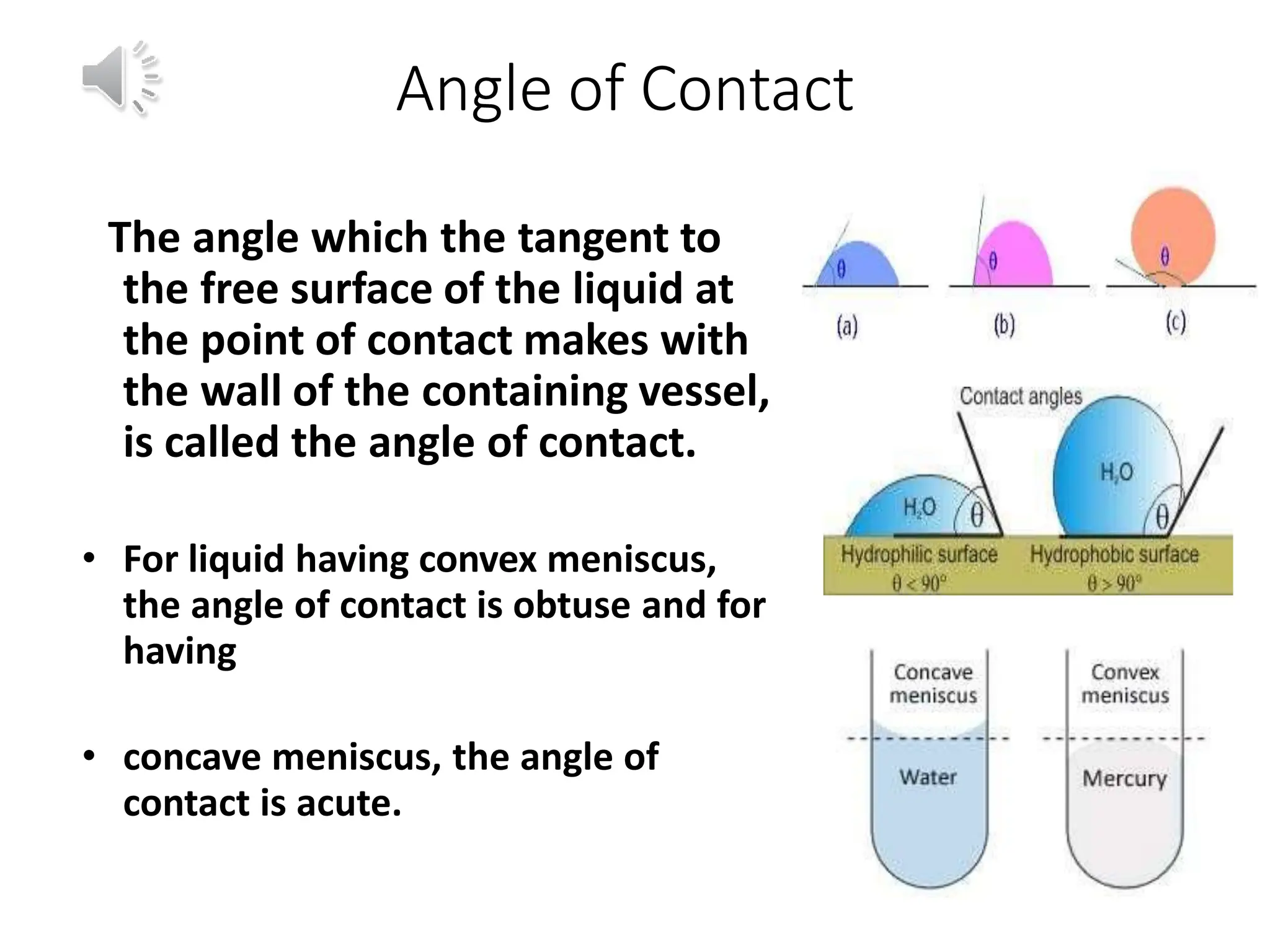
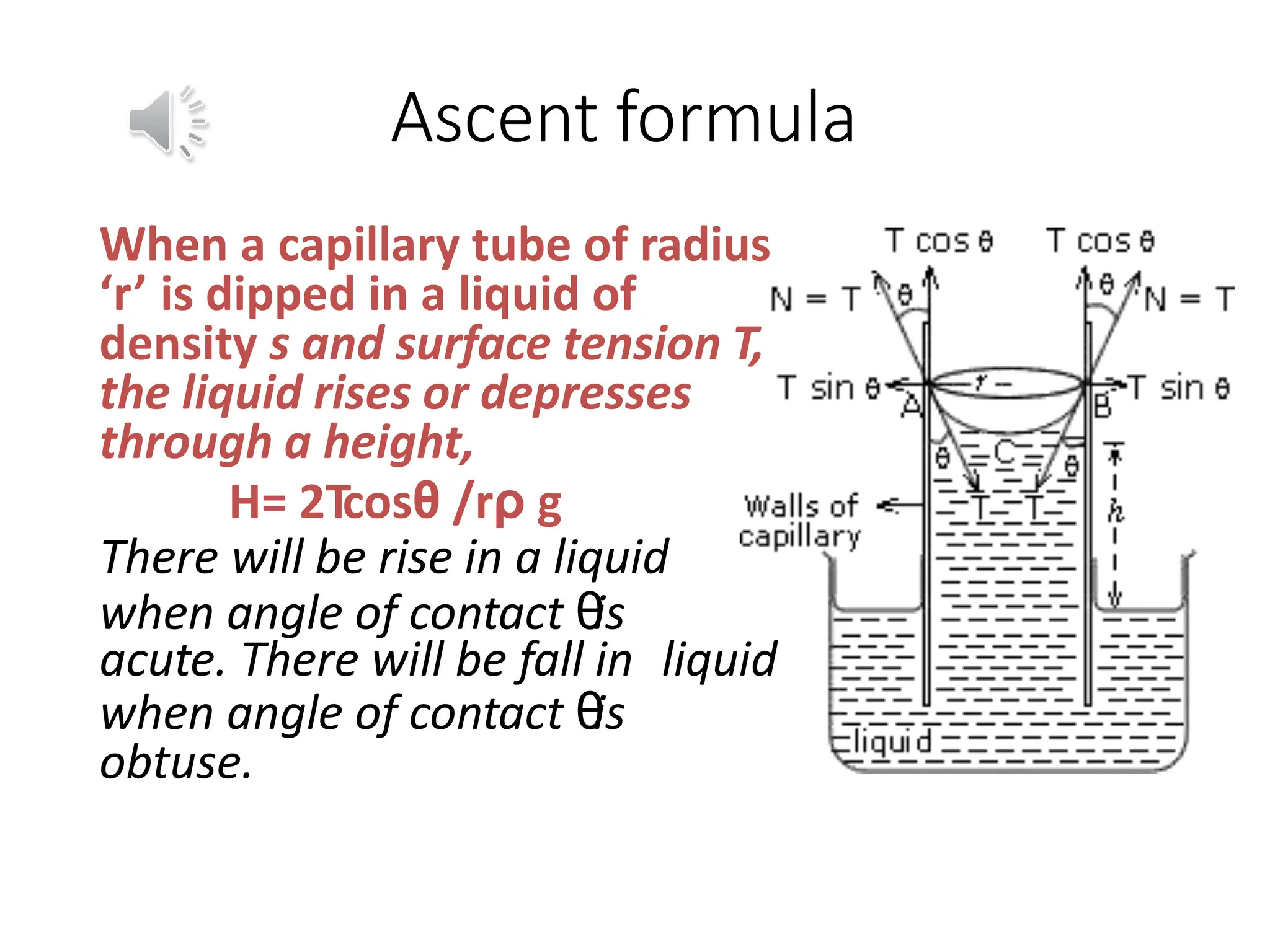
This document discusses properties of bulk matters and fluid mechanics. It defines key terms like fluid, fluid statics, pressure, viscosity, surface tension, and capillarity. It explains concepts such as variation of pressure with depth, buoyant force, Pascal's law, Bernoulli's theorem, and relationships like Poiseuille's equation, Reynolds number, and the ascent formula for capillarity. Examples are provided to illustrate how these concepts apply to situations like measuring atmospheric pressure with barometers and factors that affect whether an object will float or sink.

1. Properties of bulk
matters

2. 1–1 ■INTRODUCTION
Mechanics: The oldest physical
science that deals with both stationary
and moving bodies under the influence
of forces.
Fluid mechanics: The science that
deals with the behavior of fluids at rest
(fluid statics) or in motion (fluid
dynamics), and the interaction of fluids
with solids or other fluids at the
boundaries.
Fluid dynamics: Fluid mechanics is
also referred to as fluid dynamics by
considering fluids at rest as a special
case of motion with zero velocity.
Fluid mechanics deals
with liquids and gases in
motion or at res2t.

3. Fluid
▪ Fluid is a substance that flows under the
action of an applied force and does not have
a shape of its own.
▪ Examples: Liquids and Gases

4. Fluid Statics
• Fluid either at rest or moving in a
manner that there is no relative motion
between adjacent particles.
• No shearing stress in the fluid
• Only pressure (force that develop on
the surfaces of the particles)

5. Pressure
• Pressure is defined as a normal force
exerted by a fluid per unit area.
• Units of pressure are N/m2, which is called
a pascal (Pa).
• Since the unit Pa is too small for pressures
encountered in practice, kilopascal (1 kPa
= 103 Pa) and megapascal (1 MPa = 106
Pa) are commonly used.
• Other units include bar, atm, kgf/cm2,
lbf/in2=psi.

6. Absolute, gauge, and vacuum
pressures
• Actual pressure at a give point is called the
absolute pressure.
• Most pressure-measuring devices are calibrated
to read zero in the atmosphere, and therefore
indicate gauge pressure, Pgage=Pabs - Patm.
• Pressure below atmospheric pressure are called
vacuum pressure, Pvac=Patm - Pabs.

7. Pressure at a Point
• Pressure at any point in a fluid is the same
in all directions.
• Pressure has a magnitude, but not a
specific direction, and thus it is a scalar
quantity.

8. Pressure Exerted by a Liquid Column
F = mass of liquid in the column of depth h x g
= Volume x Density x g= Ah x ρx g
or F=Ahρg
Pressure of the liquid at a depth h is given by:
P=F/A = Ahρg/A
or P=hρg
Thus Pressure α height of fluid column & Density of fluid

9. Variation of pressure with depth
FBOTTOM - FTOP
= mg = (density x Vol) x g
FBOTTOM - FTOP = ρ
A H g
Since pressure is Force / area, Force = P x A
PBottom A – PTop A = ρ
A H g, or
PBottom – PTop
= ρ H g
The pressure below is greater
than the pressure above.
Here, PBottom = Pressure at depth
& PTop =Pa(Atmospheric Pressure)
Hence P = Pa + hρg

10. Variation of pressure with depth
Variation of pressure with depth:
P = Pa + hρg
where Pa =atmospheric pressure,
h= depth of liquid, ρ=density ,
g=acceleration due to gravity
In the presence of a gravitational field, pressure increases
with depth because more fluid rests on deeper layers.

11. Blood Pressure
• The blood pressure in
your feet can be
greater than the blood
pressure in your head
depending on whether
a person is standing
or reclining

12. How much does P increase
• At the surface of a body of water
the pressure is 1 atm
= 100,000 Pa
•As we go down into the water,
at what depth does the pressure
double, from 1 atm to 2 atm or 200,000 Pa
• Want ρg h = 100,000 Pa
1000 kg/m3 x 10 x h = 100,000
• So h = 10 meters or about 30 feet
100,000 Pa
h

13. Ans. Pressure increases
with depth, so the
speed of water leaking
from the bottom hole is
larger than that from the
higher ones.
Why speed of water
leaking from the
bottom hole is
Larger?

14. Pascal’s Law
According to this Law the Pressure applied to an
enclosed liquid is transmitted undiminished to every
point of the liquid and walls of the containing vessel.
The normal forces Fa , Fb and Fc as
shown in Fig on the faces BEFC,
ADFC and ADEB denoted by Aa , Ab
and Ac respectively.
Thus

15. Hydrostatic Paradox
• Pressure in a fluid at rest is independent
of the shape of the container.
• Pressure is the same at all points on a
horizontal plane in a given fluid.

16. A hydraulic lift
• Pressure is F / A
• At the same depth the
pressures are the same
• so F1 /A1 = F2 /A2, or
• with a little force you can
lift a heavy object!
• the jack

17. Measuring atmospheric pressure -
Barometers
Inverted closed
tube filled with
liquid The column of liquid is
held up by the pressure of
the liquid in the tank. Near
the surface this pressure
is atmospheric pressure, so
the atmosphere holds the
liquid up.
PATM
PATM
Pliquid

18. Barometric pressure
Atmospheric pressure
can support a column
of water 10.3 m high,
or a column of
mercury (which is
13.6 times as dense
as water) 30 inches
high 🡪 the mercury
barometer

19. Buoyant Force
W
PTopA
PBottomA
h
submerged object
that has a mass
density ρ
O
F = P ⋅
A
The density of the
water is ρ
W

20. Buoyant force
• The water pushes down on the top of the
object, and pushes up on the bottom of the
object
• The difference between the upward force
and the downward force is the buoyant
force FB
• since the pressure is larger on the
bottom the buoyant force is UP

21. Archimedes principle
• buoyant force is
• FB = P x A = ρ
W g h A
• • = ρ
W g (volume of object)
• • = ρ
W (volume of object) g
• • = mass of displaced water x g
• the pressure difference is ρ
W g h, so the
• F = weight of displaced water
B
• This is Archimedes principle
h
object

22. Will it float?
• The object will float if the buoyant force is
enough to support the object’s weight
• The object will displace just enough water
so that the buoyant force = its weight
• If it displaces as much water as possible
and this does not match its weight, it will
sink.
• Objects that have a density less than
water will always float.

23. VISCOSITY
•The property of a liquid by virtue of which an opposing
force(internal friction) comes into play between different layers of
a liquid whenever there is a relative motion between these layers
of the liquid is called viscosity.

24. Coefficient of Viscosity
8
The coefficient of viscosity (pronounced
‘eta’) for a fluid is defined as the ratio of
shearing stress(F/A) to the strain rate(v/l).
The SI unit of viscosity is poiseiulle (Pl). Its
other units are N s m-2 or Pa s. The
dimensions are [ML-1T-1]

25. Effect of Temperature on Viscosity
25
• The Viscosity of liquids decreases with
increase in temperature and increases
with decrease in temperature i.e. η α
• The viscosity of Gases increases with increase
in temperature and vice versa i.e. η α

26. Stoke’s Law
26
• According to Stoke’s Law the viscous
drag(F) acting on a spherical body of
radius r moving with terminal velocity v in
a fluid of coefficient of viscosity η is given
by , F=6ᴨηrv F
mg

27. Terminal Velocity
27
• When a body is dropped in a viscosity fluid, it is first
accelerated and then its acceleration becomes zero and
it attains a constant velocity called terminal velocity.
where r = radius of spherical body
η= coefficient of viscosity
σ = density of fluid
ρ = density of material of body

28. 12
Laminar versus Turbulent Flow
Laminar flow: The highly
ordered fluid motion
characterized by smooth
layers of fluid. The flow of
high-viscosity fluids such as
oils at low velocities is
typically laminar.
Turbulent flow: The highly
disordered fluid motion that
typically occurs at high
velocities and is
characterized by velocity
fluctuations. The flow of
low-viscosity fluids such as
air at high velocities is
typically turbulent.
Transitional flow: A flow
that alternates between
being laminar and turbulent. Laminar, transitional, and turbulent flows
over a flat plate.

29. Poiseuille’s Equation
29
According to Poiseuille volume of liquid coming out the tube per
second is
i)directly proportional to the Pressure difference(P)
ii) directly proportional to fourth power of radius(r) of capillary tube
iii) inversely proportional to coefficient of viscosity(η) of liquid
iv)inversely proportional to length (l) of capillary tube
i.e.
where K= ᴨ/8

30. Reynold’s Number
30
Where vc= Critical velocity of liquid
ρ = density of liquid
η = coefficient of viscosity
D= Diameter of the tube
If R< 1000 , the flow of liquid is streamline or laminar
If R> 2000, The flow is turbulent
If R lies between 1000 and 2000, the flow is unstable and may change
from streamline to turbulent flow

31. For incompressible liquid ρ1=ρ2= ρ
Then A1v1=A2v2=Av
Thus Av=Constant , This is known as equation of
continuity
31

32. Steady versus Unsteady Flow
• The term steady implies no change at a point with time.
• The opposite of steady is unsteady.
• The term uniform implies no change with location over a specified
region.
• The term periodic refers to the kind of unsteady flow in which the
flow oscillates about a steady mean.
32
.

33. Compressible versus Incompressible Flow
33
Incompressible flow: If the density of flowing fluid remains nearly
constant throughout (e.g., liquid flow).
Compressible flow: If the density of fluid changes during flow (e.g.,
high-speed gas flow)
When analyzing rockets, spacecraft, and other
systems that involve high-speed gas flows, the
flow speed is often expressed by Mach
number
Ma = 1 Sonic flow
Ma < 1 Subsonic flow
Ma > 1 Supersonic flow
Ma >> 1 Hypersonic flow

34. Bernauli’s Theorem
34

35. Applications of Bernoulli's Theorem
35

36. Limitations of Bernoulli's Theorem
36
• [1] The viscous drag has been neglected as we assume
the flow to be non-viscous.
• [2] We also used that there is no loss of energy as the
liquid moves, but some of its kinetic energy is always
converted into heat due to viscous forces.
• [3] If liquid moves along a curved path then the
centrifugal forces should also be considered.
• [4] We assume all the liquid particles moving with the
same velocity but liquid particles near the center of tube
moves faster than outer particles.

37. Cohesive & Adhesive Forces

38. Surface Tension (T)
It is the property of a liquid by
virtue of which, it behaves like
an elastic stretched
membrane with a tendency to
contract so as to occupy a
minimum surface area
• Mathematically T = F/l
• S.I Unit is : Nm-1
• Dimensional formula : M1L0T -2

39. Do you Like Hot soup or Cold Soup?
Q. Why hot soup is tastier
than cold soup?
Ans: When soup is hot its
surface tension get reduced
so it will spread on all taste
buds so is more tastier than
cold soup.

40. Surface Energy
The potential energy per unit area of the surface
film is called the surface energy.
Surface energy =
“Surface tension is numerically equal to surface energy”

41. Pressure inside a Drop or Bubble
• Excess of pressure inside a drop
and double:- There is excess of
pressure on concave side of a
curved surface
• 1. Excess of pressure inside a
liquid drop = 2T/R
• 2. Excess of pressure inside a
liquid bubble = 4T/R
• 3. Excess of pressure inside an air
bubble = 2T/R,
Where T is the surface tension ,
R = radius of liquid drop

42. Angle of Contact
The angle which the tangent to
the free surface of the liquid at
the point of contact makes with
the wall of the containing vessel,
is called the angle of contact.
• For liquid having convex meniscus,
the angle of contact is obtuse and for
having
• concave meniscus, the angle of
contact is acute.

43. Capillarity
• Capillary tube:- A tube of
very fine bore is called
capillary tube
• Capillarity:-The rise or fall
of liquid inside a capillary
tube when it is dipped in it
is called capillarity

44. Ascent formula
When a capillary tube of radius
‘r’ is dipped in a liquid of
density s and surface tension T,
the liquid rises or depresses
through a height,
H= 2Tcosθ /rρ g
There will be rise in a liquid
when angle of contact θ
is
acute. There will be fall in liquid
when angle of contact θ
is
obtuse.