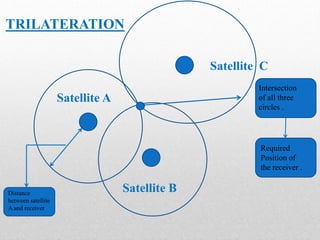
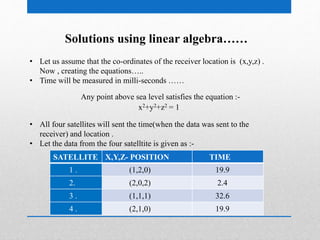
This document summarizes how GPS systems use linear algebra to determine location. It explains that GPS uses at least 3 satellites to triangulate a receiver's position via trilateration. The satellites transmit their location and arrival time. This creates a system of equations relating distance from each satellite equal to the difference between signal transmission and receipt times. Linear algebra is then used to solve the system of equations, determining the receiver's x, y, z coordinates. The process involves constructing matrices from the satellite data and time differences, then reducing them to their row echelon form to solve for position.

1. MATH
CHALLENGING ASSIGNMENT
BY :- AMIT GARG
USE OF LINEAR ALGEBRA IN GPS SYSTEM

2. GPS (GLOBAL POSTIONING SYSTEM……..)
The Global Positioning system is a space-based satellite navigation system
that provides location and time information in all weather conditions,
WORKING
• A GPS system consist of transmitter (GPS satellite ) and receiver .
• A GPS system uses 4 satellites at a time to find the location of any given
point .
• A GPS system uses a concept of TRILATERATION .
• 4th satellite is only used to increase the accuracy of the position (so
minimum 3 satellites are required to find the location of any given point )
ReceiverTransmitter

3. TRILATERATION
Intersection
of all three
circles .
Satellite A
Satellite B
Satellite C
Required
Position of
the receiver .
Distance
between satellite
A and receiver

4. A Satellite measures two things at a time…..
Time….
Location….
• Every Satellite measures the time taken to reach the electromagnetic signal from it
to the receiver .
• By multiplying it with the speed of the electromagnetic waves we can calculate the
distance between the satellite and the receiver (Radius of the circle ) .
• Satellite also sends its exact location to the receiver so that it can be taken as the
centre of the circle .

5. Solutions using linear algebra……
• Let us assume that the co-ordinates of the receiver location is (x,y,z) .
Now , creating the equations…..
• Time will be measured in milli-seconds ……
Any point above sea level satisfies the equation :-
x2+y2+z2 = 1
• All four satellites will sent the time(when the data was sent to the
receiver) and location .
• Let the data from the four satelltite is given as :-
SATELLITE X,Y,Z- POSITION TIME
1 . (1,2,0) 19.9
2. (2,0,2) 2.4
3 . (1,1,1) 32.6
4 . (2,1,0) 19.9

6. • Now , the distance between receiver and satellite is measured in terms of earth
radii per second (c = 0.047 earth radii per millisecond.)
• D=c(t-tsent) ….where t is the time when the signal is received by the receiver .
• Let (x; y; z) be the position of your GPS receiver on Earth and t be the time the
signals arrive.
• For satellite 1….
d=0.047*(t-19.9)…………(1)
By using pythagorus theorem in three dimensions…
d = 𝑥 − 1 2 + 𝑦 − 2 2 + 𝑧 − 0 2 ………(2)
• Simillarly , equations can be made for all four satellites …..
now ,
equation (1) and (2) are equal ,therefore ………..
0.047*(t-19.9)= 𝑥 − 1 2 + 𝑦 − 2 2 + 𝑧 − 0 2
squaring both sides…..we get…
(0.047*(t-19.9))2 =(x-1)2 +(y-2)2 +(z-0)2
=>2x + 4y + 0z − 2(.0472)(19.9)t = 12 + 22 + 02 − .0472(19.9)2+ x2 + y2 + z2 − .0472t2
………….(3)

7. • Simillarly , for all four satellites equations can be made but all contains same type of
squared terms of x,y,z,t.
• Therefore , these variables can be easily removed by subtracting equation 1 from
equations 2,3,4 ……
• So we get four linear equations…..which can be solved easily with the help of
matrices….
2x − 4y + 4z + 2(.0472)(17.5)t = 8 − 5 + .0472(19.92 − 2.42)
0x − 2y + 2z − 2(.0472)(12.7)t = 3 − 5 + .0472(19.92 − 32.62)
2x − 2y + 0z + 2(.0472)(0)t = 5 − 5 + .0472(19.92 − 19.92)
Other three equations are……
CONVERSION OF LINEAR EQUATIONS IN MATRIX FORM……..
2 -4 4 .077 3.86
0 -2 2 -.056 -3.47
2 -2 0 0 0
Augmented
form

8. Continuing with the solution of the system, the reduced row echelon form for
the augmented matrix is……
1 0 0 .095 5.41
0 1 0 -095 5.41
0 0 1 0.67 3.67
Reduced ech
form .
From above method we can easily calculate the position of the
receiver……
This is how a GPS network work……

9. References :- 1). https://www.youtube.com/watch?v=4O3ZVHVFhes&spfreload=1
2) Research paper of sir kalmen .