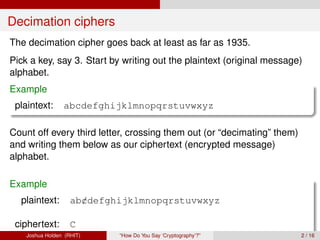
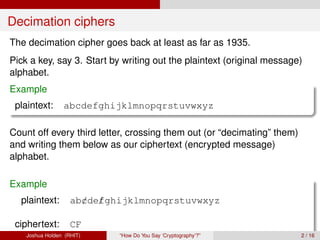
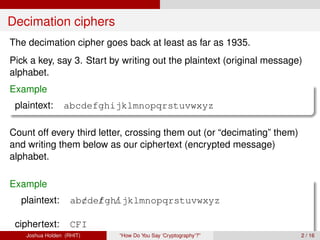
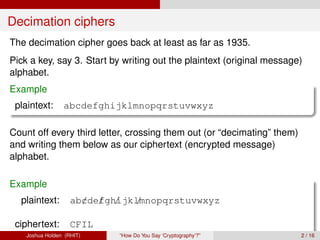
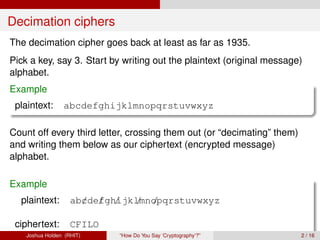
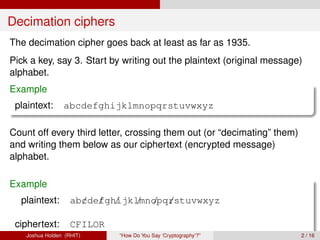
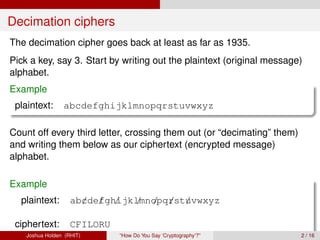
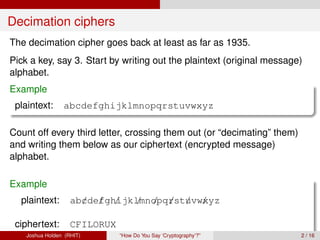
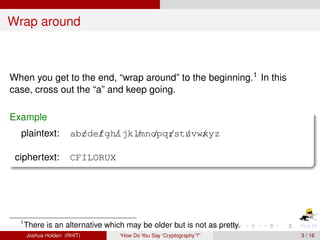
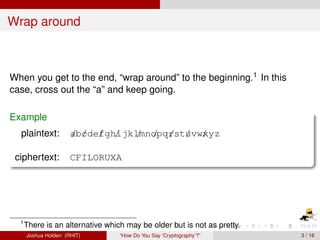
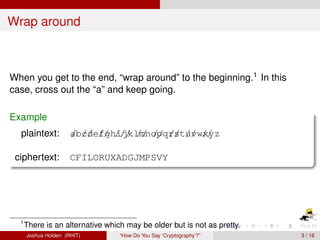
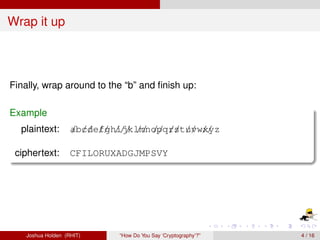
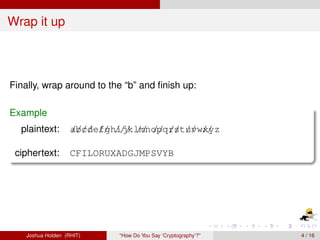
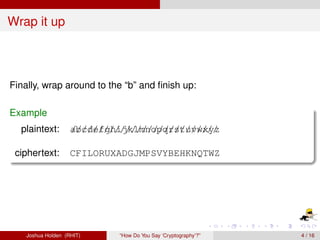
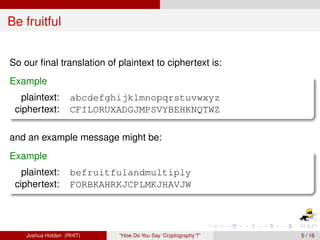
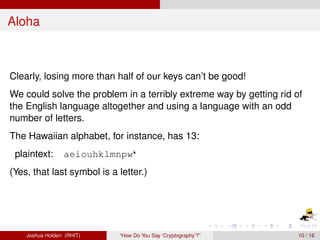
The document discusses decimation ciphers and how they relate to modular arithmetic. It explains that a decimation cipher is a type of multiplicative cipher where each letter is multiplied by a key modulo the number of letters in the alphabet. Only certain keys work well, namely those relatively prime to the alphabet size. The document explores this concept for different languages and their alphabets.

1. “How Do You Say ‘Cryptography’ in Romanian?”
Learning About Integers from Ciphers in Different
Languages
Joshua Holden
Rose-Hulman Institute of Technology
http://www.rose-hulman.edu/~holden
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 1 / 16

2. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/defghijklmnopqrstuvwxyz
c
ciphertext: C
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

3. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ ghijklmnopqrstuvwxyz
c f
ciphertext: CF
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

4. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/
c f ijklmnopqrstuvwxyz
ciphertext: CFI
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

5. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/ lmnopqrstuvwxyz
c f ijk /
ciphertext: CFIL
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

6. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/ lmnopqrstuvwxyz
c f ijk / /
ciphertext: CFILO
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

7. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/ lmnopq/stuvwxyz
c f ijk / / r
ciphertext: CFILOR
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

8. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/ lmnopq/st/vwxyz
c f ijk / / r u
ciphertext: CFILORU
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

9. Decimation ciphers
The decimation cipher goes back at least as far as 1935.
Pick a key, say 3. Start by writing out the plaintext (original message)
alphabet.
Example
plaintext: abcdefghijklmnopqrstuvwxyz
Count off every third letter, crossing them out (or “decimating” them)
and writing them below as our ciphertext (encrypted message)
alphabet.
Example
plaintext: ab/de/ gh/ lmnopq/st/vw/
c f ijk / / r u xyz
ciphertext: CFILORUX
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 2 / 16

10. Wrap around
When you get to the end, “wrap around” to the beginning.1 In this
case, cross out the “a” and keep going.
Example
plaintext: ab/de/ gh/ lmnopq/st/vw/
c f ijk / / r u xyz
ciphertext: CFILORUX
1
There is an alternative which may be older but is not as pretty.
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 3 / 16

11. Wrap around
When you get to the end, “wrap around” to the beginning.1 In this
case, cross out the “a” and keep going.
Example
plaintext: ab/de/ gh/ lmnopq/st/vw/
/ c f ijk / / r u xyz
ciphertext: CFILORUXA
1
There is an alternative which may be older but is not as pretty.
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 3 / 16

12. Wrap around
When you get to the end, “wrap around” to the beginning.1 In this
case, cross out the “a” and keep going.
Example
plaintext: ab//e// ijklmnopq/st// w/ yz
/ cd fgh/// // // r / uv x/
ciphertext: CFILORUXADGJMPSVY
1
There is an alternative which may be older but is not as pretty.
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 3 / 16

13. Wrap it up
Finally, wrap around to the “b” and finish up:
Example
plaintext: ab//e// ijklmnopq/st// w/ yz
/ cd fgh/// // // r / uv x/
ciphertext: CFILORUXADGJMPSVY
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 4 / 16

14. Wrap it up
Finally, wrap around to the “b” and finish up:
Example
plaintext: abc/e// ijklmnopq/st// w/ yz
///d fgh/// // // r / uv x/
ciphertext: CFILORUXADGJMPSVYB
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 4 / 16

15. Wrap it up
Finally, wrap around to the “b” and finish up:
Example
plaintext: abc//// h////////pq/st//// y/
///defg/ ijklmno //r //uvwx/ z
ciphertext: CFILORUXADGJMPSVYBEHKNQTWZ
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 4 / 16

16. Be fruitful
So our final translation of plaintext to ciphertext is:
Example
plaintext: abcdefghijklmnopqrstuvwxyz
ciphertext: CFILORUXADGJMPSVYBEHKNQTWZ
and an example message might be:
Example
plaintext: befruitfulandmultiply
ciphertext: FORBKAHRKJCPLMKJHAVJW
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 5 / 16

17. Letters to numbers
How can we describe the decimation method in terms of modular
arithmetic? We should translate our numbers into letters, of course.
Example
plaintext: a b c d e f g h i j ···
numbers: 1 2 3 4 5 6 7 8 9 10 ···
some operation?: 3 6 9 12 15 18 21 24 1 4 ···
ciphertext: C F I L O R U X A D ···
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 6 / 16

18. Multiplicative cipher
And now we see that a decimation cipher is the same as a
“multiplicative cipher” with multiplication by 3 modulo 26:
Example
plaintext number times 3 ciphertext
a 1 3 C
b 2 6 F
.
. .
. .
. .
.
. . . .
y 25 23 W
z 26 26 Z
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 7 / 16

19. Bad Keys
Are there any keys we can’t use? Think about multiplying by 2 — we
know that any number multiplied by 2 is even. A multiplicative cipher
with a key of 2 looks like:
Example
plaintext number times 2 ciphertext
a 1 2 B
b 2 4 D
.
. .
. .
. .
.
. . . .
m 13 26 Z
n 14 2 B
o 15 4 D
.
. .
. .
. .
.
. . . .
z 26 26 Z
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 8 / 16

20. Phi
So even keys are bad, and so is one other. (Which one?)
In fact, the bad keys are exactly those which have a common factor
with 26. Or, to put it another way:
Fact
The good keys for the multiplicative cipher are the numbers between 1
and 26 which are relatively prime to 26.
These good keys are counted by the Euler phi function, which is very
important in number theory (and cryptography):
φ(n) = # {1 ≤ k ≤ n : gcd(k , n) = 1}
φ(26) = 12, so there are 12 good keys for this cipher.
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 9 / 16

21. Aloha
Clearly, losing more than half of our keys can’t be good!
We could solve the problem in a terribly extreme way by getting rid of
the English language altogether and using a language with an odd
number of letters.
The Hawaiian alphabet, for instance, has 13:
plaintext: aeiouhklmnpw‘
(Yes, that last symbol is a letter.)
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 10 / 16

22. Two can be good, too!
So the multiplicative cipher with a key of 2 in Hawaiian looks like:
plaintext number times 2 ciphertext
a 1 2 E
e 2 4 O
i 3 6 H
o 4 8 L
u 5 10 N
h 6 12 W
k 7 1 A
l 8 3 I
m 9 5 U
n 10 7 K
p 11 9 M
w 12 11 P
‘ 13 13 ‘
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 11 / 16

23. Hawaiian keys
How many good keys are there for decimation ciphers in Hawaiian?
Since 13 is prime, every key except 13 itself is good.
φ(13) = 12 good keys, same as in English.
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 12 / 16

24. The formula for phi
A nice application of the inclusion-exclusion principle can be used to
prove:
Theorem
e
If n = p11 · · · ptet then
φ(n) = p11 − p11 −1 · · · ptet − ptet −1 .
e e
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 13 / 16

25. Danish, anyone?
So for English, we have φ(26) = (2 − 1)(13 − 1) = 12 good keys.
For Hawaiian, φ(13) = (13 − 1) = 12, also.
Spanish has 27 letters and φ(27) = (27 − 9) = 18 good keys.
Romanian has 28 letters and φ(28) = (4 − 2)(7 − 1) = 12 good keys.
Danish, Norwegian, and Swedish all have 29 letters and
φ(29) = (29 − 1) = 28 good keys.
So clearly we should be sending our secret messages in Scandinavian
languages!
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 14 / 16

26. Further developments
There is lots of other modular arithmetic that can be motivated in this
way.
You may see some of it (fixed points) in the next talk.
But if you only look at it in English, you only get to see one modulus!
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 15 / 16

27. EILWE ‘LO
and thanks for listening!
Joshua Holden (RHIT) “How Do You Say ‘Cryptography’?” 16 / 16