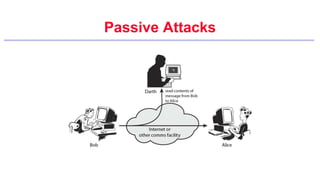
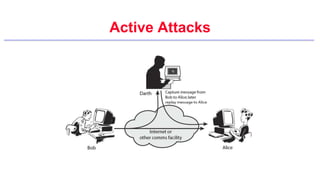
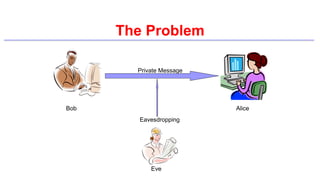
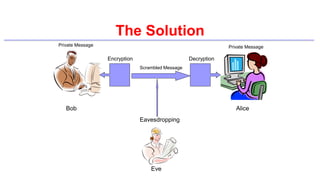
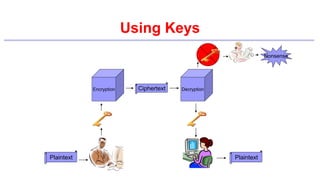
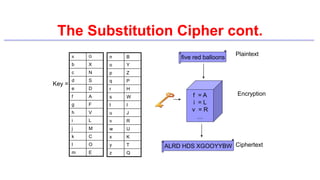
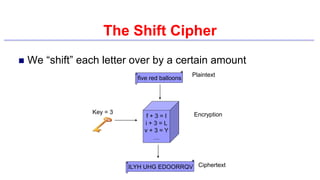
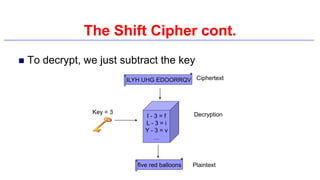
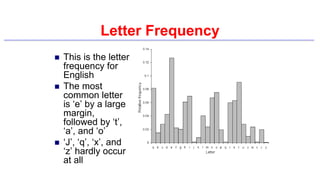
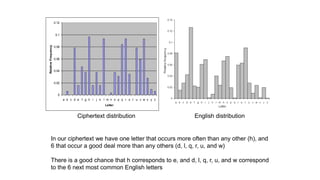
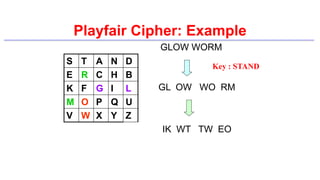
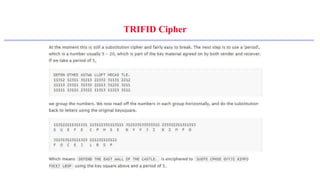
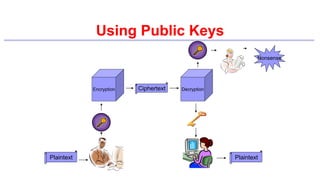
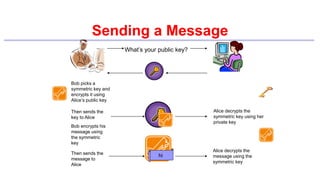
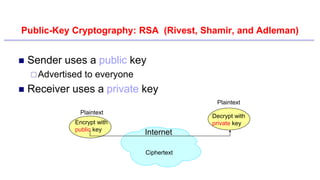
This document provides an introduction to classical ciphers and cryptography techniques. It discusses the components of information security - confidentiality, integrity and availability. It then covers various monoalphabetic and polygraphic substitution ciphers such as the Caesar, Atbash, Pigpen, Playfair and Vigenère ciphers. It also discusses transposition ciphers like the Rail Fence cipher and techniques for analyzing ciphertexts such as frequency analysis. Finally, it introduces bifid, trifid and four square ciphers. The document serves as a comprehensive overview of fundamental classical cryptography concepts.

1. Introduction to Information Security
IT Department
Noble Institute

2. CHAPTER ONE
Introduction to Information
Security

3. Security Components
 Confidentiality : Need access control, Cryptography, Existence
of data
 Integrity : No change, content, source, prevention
mechanisms, detection mechanisms
 Availability : Denial of service attacks,
 Confidentiality, Integrity and Availability ( CIA )

4. Passive Attacks

5. Active Attacks

6. Attacks
 Interception
 Interruption
 Modification
 Fabrication

7. Interception (eavesdropping)
 Unauthorized party gains access to service
or data
 Example:
Wiretapping to capture data into a network
and coping of files

8. Interruption (denial of service)
 Services or data become unavailable
 Examples:
Destruction of a piece of hardware, cutting
of cable and disabling of a file management
system

9. Modification
 Unauthorized party changes the data or
tampers with the service
 Examples:
Changing values in a file, altering a program
so that it performs differently and changing
the contents of messages that are sent over
the network

10. Fabrication
 Unauthorized party generates additional data or activity
 Examples
Hacker gaining access to a person’s email and sending
messages, and adding records to a file

11. What is cryptography?
 kryptos – “hidden”
 grafo – “write”
 Keeping messages secret
Usually by making the message unintelligible to anyone that
intercepts it

12. Some Basic Terminology
 Plaintext - original message
 Ciphertext - coded message
 Cipher - algorithm for transforming plaintext to ciphertext
 Key - info used in cipher known only to sender/receiver
 Encipher (encrypt) - converting plaintext to ciphertext
 Decipher (decrypt) - recovering ciphertext from plaintext
 Cryptography - study of encryption principles/methods
 Cryptanalysis (code breaking) - study of principles/ methods of deciphering
ciphertext without knowing key

13. The Problem
Bob Alice
Eve
Private Message
Eavesdropping

14. The Solution
Bob Alice
Eve
Scrambled Message
Eavesdropping
Encryption Decryption
Private Message Private Message

15. What do we need?
 Bob and Alice want to be able to encrypt/decrypt easily
 But no one else should be able to decrypt
 How do we do this?
Keys!

16. Using Keys
Plaintext
Ciphertext Decryption
Encryption
Plaintext
Nonsense

17. CHAPTER TWO
Monoalphabetic Cipher

18.  Atbash Cipher: simply reverses the plaintext alphabet to create
the ciphertext alphabet. That is, the first letter of the alphabet is
encrypted to the last letter of the alphabet, the second letter to the
penultimate letter and so forth.
Plaintext: ALI
Cipher text: ZOR
Atbash Cipher

19.  Pigpen Cipher: The Pigpen Cipher is another example of a substitution cipher, but rather
than replacing each letter with another letter, the letters are replaced by symbols.
Encrypt : ANT
Pigpen Cipher

20. Caesar Cipher
 Caesar Cipher: Replaces each letter by 3rd letter on
 Example:
meet me after the toga party
PHHW PH DIWHU WKH WRJD SDUWB
 Can define transformation as:
a b c d e f g h i j k l m n o p q r s t u v w x y z
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
 Mathematically give each letter a number
a b c d e f g h i j k l m n o p q r s t u v w x y z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 Then have Caesar cipher as:
c = E(k, p) = (p + k) mod (26)
p = D(k, c) = (c – k) mod (26)
 Weakness: Total 26 keys

21. The Substitution Cipher cont.
a G
b X
c N
d S
e D
f A
g F
h V
i L
j M
k C
l O
m E
ALRD HDS XGOOYYBW
five red balloons
f = A
i = L
v = R
…
Plaintext
Ciphertext
Encryption
Key =
n B
o Y
p Z
q P
r H
s W
t I
u J
v R
w U
x K
y T
z Q

22. The Shift Cipher
 We “shift” each letter over by a certain amount
ILYH UHG EDOORRQV
five red balloons
f + 3 = I
i + 3 = L
v + 3 = Y
…
Plaintext
Ciphertext
Encryption
Key = 3

23. The Shift Cipher cont.
 To decrypt, we just subtract the key
five red balloons
I - 3 = f
L - 3 = i
Y - 3 = v
…
Plaintext
Decryption
Key = 3
ILYH UHG EDOORRQV Ciphertext

24. Multiple Shift Cipher
 Shift letters according to number of shifts in each key
 a b c d e f g h i j k l m n o p q r s t u v w x y z
 Mathematically give each letter a number
 Ex
a b c d e f g h i j k l m n o p q r s t u v w x y z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Example : Kurd shift key is 3 times with ( 2, 5, 8)
KUR D
Ciphertext : MZZF
Decipher : KURD

25. Polybius Square
1) Put the letters of the alphabet in a 5X5 matrix.
2) The code for a letter is its (row, column)
3) To decode a letter look at the cell with the (row,
column). For example, 23 means row 2, column 3.

26. Example
1 2 3 4 5
1 a b c d e
2 f g h i j
3 k l m n o
4 p q r s t
5 u v w x y/z
Encode EVERYONE
15 52 15 43 55 35 34 15

27. What’s wrong with the shift cipher?
 Not enough keys!
 If we shift a letter 26 times, we get the same letter back
A shift of 27 is the same as a shift of 1, etc.
So we only have 25 keys (1 to 25)
 Eve just tries every key until she finds the right one

28. The Substitution Cipher
 Rather than having a fixed
shift, change every plaintext
letter to an arbitrary ciphertext
letter
a G
b X
c N
d S
e D
… …
z Q
Plaintext Ciphertext

29. Frequency Analysis
 In English (or any language) certain letters are used more often
than others
 If we look at a ciphertext, certain ciphertext letters are going to
appear more often than others
 It would be a good guess that the letters that occur most often in
the ciphertext are actually the most common English letters

30. Letter Frequency
 This is the letter
frequency for
English
 The most
common letter
is ‘e’ by a large
margin,
followed by ‘t’,
‘a’, and ‘o’
 ‘J’, ‘q’, ‘x’, and
‘z’ hardly occur
at all

31. Frequency Analysis in Practice
 Suppose this is our ciphertext
 dq lqwurgxfwlrq wr frpsxwlqj surylglqj d eurdg vxuyhb ri wkh glvflsolqh dqg
dq lqwurgxfwlrq wr surjudpplqj. vxuyhb wrslfv zloo eh fkrvhq iurp: ruljlqv ri
frpsxwhuv, gdwd uhsuhvhqwdwlrq dqg vwrudjh, errohdq dojheud, gljlwdo
orjlf jdwhv, frpsxwhu dufklwhfwxuh, dvvhpeohuv dqg frpslohuv, rshudwlqj
vbvwhpv, qhwzrunv dqg wkh lqwhuqhw, wkhrulhv ri frpsxwdwlrq, dqg
duwlilfldo lqwhooljhqfh.

32. 0
0.02
0.04
0.06
0.08
0.1
0.12
a b c d e f g h i j k l m n o p q r s t u v w x y z
Letter
Relative
Frequency
Ciphertext distribution English distribution
In our ciphertext we have one letter that occurs more often than any other (h), and
6 that occur a good deal more than any others (d, l, q, r, u, and w)
There is a good chance that h corresponds to e, and d, l, q, r, u, and w correspond
to the 6 next most common English letters

33. CHAPTER THREE
Polygraphic and Transportation
Cipher

34. Playfair Cipher
• The Playfair Cipher operates on pairs of letters (bigrams).
• The key is a 5x5 square consisting of every letter except J.
Before encrypting, the plaintext must be transformed:
• Replace all J’s with I’s
• Write the plaintext in pairs of letters…
• separating any identical pairs by a Z
• If the number of letters is odd, add a Z to the end

35. Playfair Cipher: Encryption
 If two plaintext letters lie in the same row then replace each letter
by the one on its “right” in the key square
 If two plaintext letters lie in the same column then replace each
letter by the one “below” it in the key square
 Else, replace:
 First letter by letter in row of first letter and column of second letter in the
key square
 Second letter by letter in column of first letter and row of second letter in
the key square

36. Playfair Cipher: Example
S T A N D
E R C H B
K F G I L
M O P Q U
V W X Y Z
GLOW WORM
GL OW WO RM
IK WT TW EO
Key : STAND

37. Vigenère Cipher
• The Vigenère cipher uses a 26×26 table with A to Z as the row heading and
column heading.
• This table is usually referred to as the Vigenère Tableau, Vigenère
Table or Vigenère Square.
• We shall use Vigenère Table.
• The first row of this table has the 26 English letters.
• Starting with the second row, each row has the letters shifted to the left one
position in a cyclic way. For example, when B is shifted to the first position on the
second row, the letter A moves to the end.

38. Vigenère Cipher

39. Vigenère Cipher
Example: MICHIGAN TECHNOLOGICAL UNIVERSITY keyword: HOUGHTON

40. Decipher Vigenère Cipher
To decrypt, pick a letter in the ciphertext and its corresponding letter in the
keyword, use the keyword letter to find the corresponding row, and the letter
heading of the column that contains the ciphertext letter is the needed plaintext
letter. For example, to decrypt the first letter T in the ciphertext, we find the
corresponding letter H in the keyword. Then, the row of H is used to find the
corresponding letter T and the column that contains T provides the plaintext
letter M (see the above figures). Consider the fifth letter P in the ciphertext. This
letter corresponds to the keyword letter H and row H is used to find P. Since P is
on column I, the corresponding plaintext letter is I.

41. Beaufort Cipher
• The 'key' for a beaufort cipher is a key word. e.g. 'FORTIFICATION’.
• The following assumes we are enciphering the plaintext letter D with the key
letter F) Now we take the letter we will be encoding, and find the column on the
tableau, in this case the 'D' column. Then, we move down the 'D' column of the
tableau until we come to the key letter, in this case 'F' (The 'F' is the keyword
letter for the first 'D'). Our ciphertext character is then read from the far left of the
row our key character was in, i.e. with 'D' plaintext and 'F' key, our ciphertext
character is 'C'.

42. the columns according to the key before reading off .
Transposition (Permutation) Ciphers
 Rearrange the letter order without altering the actual letters
 Rail Fence Cipher: Write message out diagonally as:
m e m a t r h t g p r y
e t e f e t e o a a t
 Giving ciphertext: MEMATRHTGPRYETEFETEOAAT
 Row Transposition Ciphers: Write letters in rows, reorder
Key: 4312567
Column Out 4 3 1 2 5 6 7
Plaintext: a t t a c k p
o s t p o n e
d u n t i l t
w o a m x y z
Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ

43. CHAPTER FOUR
BIFID, TRIFID and Four Square
Cipher

44. BIFID Cipher
 Bifid is a 5 by 5 matrix cipher which combines the Polybius
square with transposition, and uses fractionation to achieve
diffusion. It was invented by Felix.

45. TRIFID Cipher
 Trifid is very similar to Bifid, except that instead of a 5 by 5 key square (in
bifid) we use a 3 by 3 by 3 key cube.

46. TRIFID Cipher

47. Four Square Cipher
• The Four-square cipher encrypts pairs of letters (like playfair), which makes it significantly
stronger than substitution ciphers etc. since frequency analysis becomes much more difficult.
• The four-square cipher uses four 5 by 5 matrices arranged in a square. Each of the 5 by 5
matrices contains 25 letters, usually the letter 'j' is merged with 'i’.In general, the upper-left
and lower-right matrices are the "plaintext squares" and each contain a standard alphabet. The
upper-right and lower-left squares are the "ciphertext squares" and contain a mixed alphabetic
sequence.

48. Four Square Cipher

49. Four Square Cipher

50. CHAPTER FIVE
Public Key Encryption

51. Public Key Cryptography
 Diffie and Hellman published a paper in 1976
providing a solution
 We use one key for encryption (the public key)
and a different key for decryption (the private key)
 Everyone knows Alice’s public key, so they can
encrypt messages and send them to her
 But only Alice has the key to decrypt those messages
 No one can figure out Alice’s private key even if
they know her public key

52. Using Public Keys
Plaintext
Ciphertext Decryption
Encryption
Plaintext
Nonsense

53. Public Key Cryptography in Practice
 The problem is that public key algorithms are too slow to encrypt
large messages
 Instead Bob uses a public key algorithm to send Alice the symmetric key,
and then uses a symmetric key algorithm to send the message
 The best of both worlds!
 Security of public key cryptography
 Speed of symmetric key cryptography

54. Sending a Message
What’s your public key?
Bob picks a
symmetric key and
encrypts it using
Alice’s public key
Alice decrypts the
symmetric key using her
private key
Then sends the
key to Alice
Bob encrypts his
message using
the symmetric
key
Then sends the
message to
Alice
Alice decrypts the
message using the
symmetric key
hi

55. The RSA Public Key Cipher
 The most popular public key cipher is RSA, developed in 1977
 Named after its creators: Rivest, Shamir, and Adleman
 Uses the idea that it is really hard to factor large numbers
 Create public and private keys using two large prime numbers
 Then forget about the prime numbers and just tell people their product
 Anyone can encrypt using the product, but they can’t decrypt unless they know the
factors
 If Eve could factor the large number efficiently she could get the private key, but there is
no known way to do this

56. Public-Key Cryptography: RSA (Rivest, Shamir, and Adleman)
 Sender uses a public key
Advertised to everyone
 Receiver uses a private key
Internet
Encrypt with
public key
Decrypt with
private key
Plaintext
Plaintext
Ciphertext

57. Generating Public and Private Keys
 Choose two large prime numbers p
and q (~ 256 bit long) and multiply
them: n = p*q
 Chose encryption key e such that e
and (p-1)*(q-1) are relatively prime
 Compute decryption key d, where
d = e-1 mod ((p-1)*(q-1))
(equivalent to d*e = 1 mod ((p-1)*(q-1)))
 Public key consists of pair (n, e)
 Private key consists of pair (n, d)

58. RSA Encryption and Decryption
 Encryption of message block m:
 c = me mod n
 Decryption of ciphertext c:
 m = cd mod n

59. Example (1/2)
 Choose p = 7 and q = 11  n = p*q = 77
 Compute encryption key e: (p-1)*(q-1) =
6*10 = 60  chose e = 13 (13 and 60 are
relatively prime numbers)
 Compute decryption key d such that 13*d
= 1 mod 60  d = 37 (37*13 = 481)

60. Example (2/2)
 n = 77; e = 13; d = 37
 Send message block m = 7
 Encryption: c = me mod n = 713 mod 77 = 35
 Decryption: m = cd mod n = 3537 mod 77 = 7